

 Vol. 38 (Nº 60) Año 2017. Pág. 7
Vol. 38 (Nº 60) Año 2017. Pág. 7
Bergson Rodrigo Siqueira de MELO 1; Maria Socorro Lucena LIMA 2; Otávio Paulino LAVOR 3; Verônica Maria Lavor Silva de MELO 4
Recibido: 13/08/2017 • Aprobado: 05/09/2017
RESUMO: A compreensão do conceito de Cálculo Diferencial e Integral é essencial para auxiliar na aprendizagem dos alunos em cursos de Engenharias. Espera-se uma motivação para a prática discente ao oportunizar uma nova perspectiva do ensino e aprendizagem desses conceitos matemáticos, dentre os quais estão àqueles ligados ao pensamento específico dessa disciplina que é básico para o andamento das disciplinas subsequentes. E tendo em vista uma necessidade de motivação, a prática docente pode oportunizar novas perspectivas ao relacionar os conceitos de cálculo com outras disciplinas do curso. Neste contexto, este trabalho objetiva quantificar e analisar a motivação e a visão de um grupo de alunos tomados de forma aleatória, em respeito às aulas de cálculo ministradas a partir dos conceitos interligados às outras disciplinas. Foram aplicados questionários nos quais os discentes puderam responder algumas perguntas estruturadas do tipo objetivas que avaliam se o professor fez aplicações do cálculo diferencial e integral e onde essas aplicações foram feitas, bem como se as aplicações geram um melhor entendimento do assunto e se os professores devem sempre ter essa prática de relacionar o cálculo diferencial e integral. Assim, foi possível verificar que os alunos afirmam ter estudado o cálculo relacionado com outros conceitos de física e engenharias. A maioria afirma ainda que tem interesse nestas relações de conceitos e acredita que isso contribui bastante para o aprendizado. Então, destas respostas discentes, pode-se trabalhar melhor o currículo relacionando um conceito com outro na tentativa de sanar diversas lacunas motivacionais que podem refletir na mudança de postura frente à motivação para compreenderem os novos conceitos matemáticos. |
ABSTRACT: The understanding of the concept of Differential and Integral Calculus is essential to assist in students learning in Engineering courses. The motivation for the student practice is expected to provide a new perspective on the teaching and learning of these mathematical concepts, among which are those related to the specific thinking of this discipline that is basic to the course of subsequent disciplines. And in view of a need for motivation, the teaching practice can provide new perspectives by relating the concepts of calculation with other subjects of the course. In this context, this paper aims to quantify and analyze the motivation and the vision of a group of students taken in a random way, with respect to the calculation classes taught from the concepts interconnected to the other disciplines. Questionnaires were used in which students could answer some structured objective questions that assess whether the teacher made applications of differential and integral calculus and where these applications were made, as well as if the applications generate a better understanding of the subject and if the teachers should Always have this practice of relating differential and integral calculus. Thus, it was possible to verify that the students claim to have studied the calculation related to other concepts of physics and engineering. Most people still say that they are interested in these concept relations and believe that this contributes greatly to learning. Hen, from these students' responses, one can better work on the curriculum by relating one concept to another in an attempt to remedy several motivational gaps that may reflect the change in posture versus the motivation to understand the new mathematical concepts. |
O ensino de Cálculo Diferencial e Integral vem sendo estudado e debatido por uma gama de pesquisadores na atualidade. Nos diversos cursos superiores que necessitam dessa disciplina como pré-requisito básico, como as várias engenharias, nos quais os alunos se deparam com a mesma logo nos primeiros semestres, é percebido um alto índice de reprovação (BORGES e MORETTI, 2016) e em consequência grande evasão.
É consenso por partes dos professores de Cálculo mencionar que os alunos precisam superar essa barreira inicial com esse conhecimento em desenvolvimento, pois o sucesso ou insucesso nesses cursos também perpassa essa superação, ou seja,
“(...) o perfil do ingressante não corresponde àquele desejado pela universidade. Transformar o aluno em um acadêmico com hábitos eficientes de estudo, capacidade de expressão escrita e pré-requisitos para o Cálculo é entendida como uma desafiante tarefa dos professores de matemática dos primeiros anos da graduação.” (BORGES e MORETTI, 2016, pág. 486)
Alguns pesquisadores (NASSER, 2007; CURI e FARIAS, 2008; SANTOS e NETO, 2008) realizaram estudos investigando os motivos pelos quais os estudantes apresentam baixos rendimento com relação a essa disciplina e apontam possíveis meios de superação das dificuldades através de práticas pedagógicas diferenciadas e mudança de método de estudo por parte dos alunos. Outros estudiosos assinalam que as dificuldades são trazidas desde a matemática básica do Ensino Médio (SOBRINHO et al., 2005).
Assim, com esses estudos apontando que os alunos não tem uma base adequada para cursarem o Cálculo, trazendo suas deficiências desde o ensino básico, e por outro lado, considerando que na faculdade existe uma inquietação dos mesmos em saber a real necessidade da aplicação dos conhecimentos desse conteúdo, pode-se procurar desenvolver um impulso de superação da referida barreira via essa motivação de procurarem perceber a aplicabilidade desses conceitos matemáticos em outras disciplinas que são cursadas no mesmo período.
Tal concepção pedagógica de investigações matemáticas em sala de aula se justifica por trabalhar o conceito a partir das ideias de aplicação em outros assuntos que deram origem ao próprio Cálculo, bem como abordar o estudo por meio de resolução de problemas de outras disciplinas, já bem elencado na literatura.
E essa proposta de trabalho, que tem sua origem ou inspiração no trabalho investigativo dos cientistas empíricos e desenvolvem a necessidade de comprovação e aplicação dos resultados, enfatiza o que aborda Borges e Moretti (2016), ao citarem Charlot (2000) para justificar a situação de fracasso escolar, aqui usada como sinônimo da já referida barreira inicial, uma vez que,
“tal atitude se conecta à importância que o aluno dá à atividade escolar e ao conhecimento, visto que a dedicação à atividade intelectual depende de uma pré-disposição a aprender, uma aceitação, por alguma razão, do conhecimento”. (CHARLOT, 2000, p.30 apud BORGES e MORETTI, 2016, pág. 486)
E ver-se tal razão nessa motivação percebida, e objeto de investigação no presente trabalho, de procurarem a já mencionada aplicabilidade desses conceitos relacionados com outras disciplinas do currículo, pois os engenheiros vão utilizar na prática esses conhecimentos quando estiverem em seu campo de atuação como, por exemplo, o engenheiro civil que precisar calcular a quantidade de cimento para determinada construção ou um engenheiro mecânico, que necessita saber o nível de resistência de certos materiais.
Nesse sentido, no trabalho em sala de aula com Cálculo, pretende-se resgatar as suas possíveis relações com outros itens curriculares e promover uma reflexão prática sobre a construção do conhecimento matemático, entretanto sabemos que as investigações matemáticas naturalmente tratam de conceitos, procedimentos e representações matemáticas, já que “os saberes têm especificidades de conteúdos, de reconhecimento social e de linguagem”, conforme Borges e Moretti (2016).
Porém, aparentemente o que mais motiva os alunos, a saber, é a sua possível aplicação prática, refletindo o que as pesquisas da relação com o saber têm destacado, segundo Borges e Moretti (2016), com “a atribuição de sentidos para a Matemática e seu ensino, mais pelo campo da importância social, profissional, do histórico escolar e do gosto, do que pela natureza do conhecimento matemático, sua linguagem e estrutura”. Por outro lado a pesquisa realizada por (MELO et al, 2016), traz um estudo sobre a visão discente de um curso de Licenciatura em Matemática, onde a motivação dos respectivos alunos seria os elementos da tecnologia e a interação entre eles e professores, onde os autores procuraram identificar através das falas dos sujeitos da pesquisa os seus pontos de vista em relação ao curso que fazem, trazendo a tona o que eles pensam sobre alguns elementos do curso.
E nesse viés, durante as aplicações e intervenções docentes em sala de aula é esperado que os alunos possam de forma geral e consistente, utilizar processos que caracterizem a atividade de investigação Matemática em atividades direcionadas para o Cálculo, compreendemos que aulas diferenciadas podem ser uma linha motivacional.
Nesse contexto, este trabalho objetiva verificar a satisfação dos discentes em relação às práticas de cálculo aplicado a outras disciplinas, detalhando assim uma relação motivacional dos alunos com o Cálculo para superação das barreiras iniciais, justificando sua importância visto que, concordando com Borges e Moretti (2016) apud Silva (2008) “faltam pesquisas que detalhem as relações dos alunos com a Geografia, a Biologia, a Física, a Matemática e as demais disciplinas”, além de ter como finalidade em si, obter conhecimento de seus anseios para melhorar o planejamento e a prática pedagógica.
Os cursos de engenharias da Universidade Federal Rural do Semi-Árido contém um clico básico chamado de Bacharelado em Ciência e Tecnologia. É nesta fase que o discente tem contato com as disciplinas de cálculo diferencial e integral. Verificando se a superação das dificuldades iniciais em busca de um melhor desempenho nas aulas de cálculo está nas aplicações feitas a outras disciplinas, uma investigação é feita para descobrir e compreender a visão dos discentes em relação às aulas aplicadas, bem como aos seus anseios em relação às práticas pedagógicas.
Para fazer tal investigação, uma amostra de dezoito discentes foi tomada de forma aleatória. Esses discentes responderam questionários com perguntas objetivas que avaliam se o professor fez aplicações do cálculo diferencial e integral e onde essas aplicações foram feitas. Os discentes responderam ainda, se as aplicações geram um melhor entendimento do assunto, bem como se os professores devem ter essa prática de aplicações do cálculo diferencial e integral.
Tendo a citada Universidade Federal como campo de estudo amostrado pelos dezoito discentes, propõe-se investigar a motivação como na visão de Charlot (2000) apud Borges e Moretti (2016), que é uma ação de fora para dentro do sujeito, mas aqui tentando visualizar se gera mobilização, também como define aquele, ou seja, ação do sujeito para ele mesmo a parti de suas convicções.
As respostas aos questionários foram analisadas e os resultados mostram o posicionamento dos discentes em relação às aplicações do cálculo diferencial. Primeiramente, buscou-se ter conhecimento se os professores que ministram as disciplinas de cálculo relacionam os conceitos de cálculo com os conceitos de outras disciplinas. As respostas a este quesito estão apresentadas no gráfico da figura 1.
Figura 1
O cálculo relacionado com outras disciplinas
Como pode ser visto no gráfico, dos dezoito discentes, dezesseis afirmam que o professor de cálculo relaciona os conceitos com outras disciplinas. Dessa forma, acredita-se que os professores de cálculo usam essa abordagem como motivação para o ensino destas disciplinas.
Sendo o cálculo aplicado e relacionado em outras disciplinas do curso, buscou-se saber onde estas aplicações se concentram dentro do curso. O gráfico da figura 2 mostra as respostas dos discentes.
Figura 2
Disciplinas em que o cálculo foi relacionado

A maioria das aplicações se concentrou na área de física, onde dois terços dos discentes afirmam que esta é a área em que o professor mais faz as aplicações. Esta área tem as maiores aplicações do cálculo devido a sua proximidade com a matemática, bem como por ter suas disciplinas ministradas de forma concomitantes com as disciplinas de cálculo. Nas palavras de um matemático, tem-se:
“As aplicações são feitas de forma as disciplinas de um mesmo período possam estar próximas umas das outras. Por exemplo: as primeiras disciplinas de cálculo são ministradas no mesmo semestre que a disciplina de mecânica clássica. Então, entendo que seja interessante que estas disciplinas estejam próximas e uma sirva de motivação para a outra”.
Foi visto acima que os professores relaciona suas aulas de cálculo com outras disciplinas para que as aplicações sejam motivações que estimulem o desejo e o aprendizado do cálculo, destacando a que se propõe esta investigação, motivação com a finalidade de gear mobilização. Mas será que os discentes estão interessados nestas aplicações? Já que, como destacado por Borges e Moretti (2016), para Charlot (2000),
“mobilização [...] é uma ação do sujeito para ele mesmo, é o que movimenta o sujeito, a partir de suas convicções, a engajar-se em uma atividade de aprender. Assim, do desejo pelo saber, o sujeito mobiliza-se para aprender”. (CHARLOT, 2000, p. 55 e CHARLOT, 2007, p. 100 apud Borges e Moretti, 2016, 489).
O gráfico da figura 3 mostra o quanto os discentes tem interesse na relação dos conceitos de cálculo com outras disciplinas.
Figura 3
Interesse nas aplicações

Como pode ser visto, é quase unânime que os discentes têm interesse pela relação de cálculo com outras disciplinas. Apenas um discente afirma não ter interesse nestas aplicações em outras disciplinas.
Uma vez que a maioria dos discentes está interessada, acredita-se que as aplicações podem ser motivação para um melhor aprendizado, ou seja, gera mobilização. Mas qual a opinião dos discentes? Será que eles também acreditam nisso? Isso porque são as relações epistêmicas que definem a forma de dedicação, pesquisa e compreensão nas atividades de aprender, aqui entendidas como necessárias a superação das barreiras iniciais, e aquelas dependem de como o sujeito entende o saber, sua estrutura e suas características (BORGES E MORETTI, 2016).
O gráfico da figura 4 mostra as respostas em relação a opinião discente do aprendizado contribuído pela relação dos conceitos de cálculo com outras disciplinas.
Figura 4
Contribuição da relação dos conceitos de cálculo com outras disciplinas.

Também é quase unânime que os discentes acreditam que a relação com outras disciplinas ajudam no entendimento do cálculo. Um discente do curso faz a seguinte afirmação;
“O cálculo me parece difícil de ser compreendido, no entanto quando vejo a quantidade de aplicações e sua proximidade com as outras disciplinas, me sinto motivado a estudar mais visto que percebo que meu esforço será útil em todas as disciplinas, não simplesmente no cálculo. Uma disciplina relacionada com outra fica parecendo que estudamos uma coisa só”.
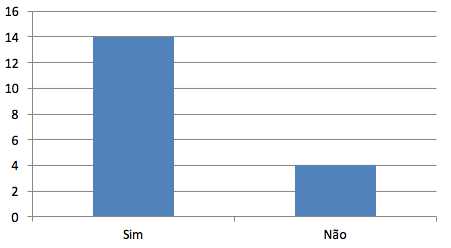
Por último, foi investigado se a relação dos conceitos de cálculo com outras disciplinas deve ser feita por todos os professores da área. O gráfico da figura 5 mostra as respostas.
Figura 5
Obrigação da relação de cálculo com outras disciplinas.

Dos dezoito alunos que responderam ao questionário, catorze acreditam que a relação de cálculo com outras disciplinas deve ser feita por todos os professores da área. Aqui, se percebe que alguns alunos, mesmo tendo interesse e acreditando que auxilia o aprendizado, entendem que os professores não podem ser obrigados a relacionar cálculo com outras disciplinas.
Dessa forma, os resultados apresentados propõem que, na percepção dos discentes, as aplicações como motivação geram mobilização dos mesmos para superarem suas barreiras iniciais, aqui vistas como ausência do desejo de aprender gerando falta de esforço.
A aplicação do questionário para averiguação da visão discente frente às relações com outras disciplinas como motivação no ensino de Cálculo reafirmou a suspeita de que estas são vistas tanto, de forma indireta, pelos docentes como pelos discentes pesquisados como um fator de regulação do distanciamento com o saber que necessita de mobilização em relação à aprendizagem.
Assim, há uma relação motivacional dos alunos com o Cálculo para superação das barreiras iniciais, sejam elas geradas ou não pelas dificuldades advindas do Ensino Médio, que perpassa o uso de aplicações em outras disciplinas, algo que se justifica, pois:
“na relação com o saber o sujeito constrói-se a si mesmo, transformando-se a partir do que aprende. Nesse processo, os medos, as angústias, as inseguranças e as certezas aparecem de forma particular em cada sujeito, moldando as relações com o saber.” (BORGES E MORETTI, 2016, pág. 490).
Dessa forma, a importância do presente trabalho está em apontar uma relação que, na visão dos discentes, se pauta em uma ação externa (motivação) que gera uma ação interna (mobilização). Fato que, possibilita disponibilizar mais um conhecimento para as constantes reflexões críticas que embasam o planejamento e a prática pedagógica.
BORGES, P. A. P. e MORETTI, M. T. A relação com o saber matemático de alunos ingressantes na universidade. Educação Matemática Pesquisa, São Paulo, v. 18, n. 1, 485-510, 2016.
CURI, R. C., FARIAS, R. M. S. Métodos de estudo e sua influência no desempenho dos alunos em disciplinas de cálculo diferencial e integral. In: Congresso Brasileiro de Ensino de Engenharia, 2008. São Paulo. Anais. São Paulo: 2008.
MELO, B.R.S; SILVANO, A. M. C; LAVOR, O.P; BATISTA, P.C.S. As contribuições pedagógicas por meio do ambiente virtual de aprendizagem (AVA), na visão dos alunos do curso de Licenciatura em Matemática semipresencial. In: XII ENCONTRO NACIONAL DE EDUCAÇÃO MATEMÁTICA - XII ENEM, Anais. São Paulo, SP: UNICSUL, 2016.
NASSER, L. Ajudando a superar obstáculos na aprendizagem de cálculo. In: Encontro Nacional de Educação Matemática, 2007. Belo Horizonte. Anais. Belo Horizonte: 2007.
SANTOS, R. M., NETO, H. B. Avaliação do desempenho no processo de ensino-aprendizagem de cálculo diferencial e integral I (O caso da UFC). In: Congresso Brasileiro de Ensino de Engenharia, 2008. São Paulo. Anais. São Paulo: 2008.
SOBRINHO, J. C., DECHECHI, E. C., DETONI, M. M. Dificuldades conceituais em matemática básica de ingressantes no curso de engenharia de produção agroindustrial. In: Congresso Brasileiro de Ensino de Engenharia, 2005. Campina Grande. Anais. Campina Grande: 2005.
1. Programa de Pós-Graduação em Educação –PPGE - Universidade Estadual do Ceará – UECE – Fortaleza - CE. email: bergson1melo@gmail.com
2. Programa de Pós-Graduação em Educação –PPGE - Universidade Estadual do Ceará – UECE – Fortaleza - CE. email: socorro_lucena@uol.com.br
3. Universidade Federa Rural do Semi-Árido - UFERSA – Pau dos Ferros - RN. email: otavio.lavor@ufersa.edu.br
4. Secretaria Municipal de Educação - SME – Fortaleza - CE. email: veronica.lavor@yahoo.com