

 Vol. 38 (Nº 60) Año 2017. Pág. 4
Vol. 38 (Nº 60) Año 2017. Pág. 4
MANSILHA, Marcio B. 1; FARRET, Felix A. 2; KULLMANN, Deise H. 3
Recibido: 10/08/2017 • Aprobado: 05/09/2017
RESUMO: Neste artigo apresentamos o método simplex. É feita uma explanação sobre o método simplex e programação linear. Por fim, um de problema de programação linear é resolvido através do método simplex detalhadamente e os resultados são comparados aos obtidos usando-se um software de programação linear, mostrando que os resultados fornecidos são iguais. Ainda, os resultados obtidos através do método simplex são comparados aos obtidos através do método gráfico, mostrando que as soluções encontradas correspondem aos vértices do método gráfico. |
ABSTRACT: In this article we present the simplex method. An explanation is made on the simplex method and linear programming. Finally, a linear programming problem is solved through the simplex method in detail and the results are compared to those obtained using linear programming software, showing the results provided. The results obtained through the simplex method are compared to those obtained through the graphical method, showing that the solutions found correspond to the vertices of the graphical method |
A Programação Linear (PL) é talvez o problema de otimização mais importante e bem estudado. Problemas do mundo real podem ser formulados como problemas de programação linear. A PL é o processo de minimizar ou maximizar a função objetivo linear a uma série de igualdades e desigualdades de restrições lineares. O algoritmo simplex é o método mais utilizado para a resolução de problemas de programação linear (PLOSKAS; SAMARAS, 2015). O Método simplex (Dantzig) para programação linear foi criado por George Dantzig em 1947. O sucesso do algoritmo levou a uma vasta gama de especializações e generalizações que têm dominado a pesquisa de operações práticas desde então (DANTZIG; THAPA, 2003),(NEZAMABADI; VAHIDINASAB, 2015)(NASH, 2000),(SOUSA, 2005). O Método simplex é um procedimento matricial para resolver o modelo de programação linear na forma normal. Refere-se a família dos métodos de otimização globais, conhecidos como métodos de procura direta (DAVOODI; HAGH; ZADEH, 2014). Os recentes avanços de hardware tornaram possível resolver problemas de PL em grande escala em um curto espaço de tempo. Unidades de Processamento gráfico (GPUs) ganharam muita popularidade e têm sido aplicados para algoritmos lineares de programação (PLOSKAS; SAMARAS, 2015).
Na próxima seção será apresentada a formulação para o problema de PL. Na terceira seção deste artigo é apresentada a metodologia por trás do método simplex.
Após, é apresentado um exemplo resolvido passo a passo pelo método simplex e seus resultados são comparados aos obtidos utilizando-se o software otimiza.
O problema de programação linear consiste de um problema de otimização, ou seja, consiste na alocação de recursos limitados a atividades em competição, de forma ótima.
A forma matemática clássica de apresentação do problema de programação linear é a seguinte:

Método simplex é um método interativo utilizado para se determinar, numericamente, a solução ótima de um modelo de Programação Linear. Para Ploskas e Samaras (PLOSKAS; SAMARAS, 2014) a escolha do elemento de articulação em cada iteração é um dos passos mais críticos para o algoritmo simplex. A flexibilidade da seleção de variáveis que entram e saem permite desenvolver várias regras de articulação. No trabalho de San e Chen (SAN; CHEN, 2007), é proposto um algoritmo híbrido melhorado-simplex genética (HSIGA), que combina o método simplex (SM) e algoritmo genético (GA) para resolver problemas de otimização numérica globais.
Tan, Chin e Dou (TAN; CHIN; DOU, 2003) em seu artigo utilizam o modelo de sinal de ativação que é identificado através do método de “downhill simplex” multidimensional onde os resultados em tempo real, verificar a eficácia do esquema proposto.
Diversos autores utilizaram o Método Simplex para resolver problemas de engenharia (YAMAMURA; KITAKAWA, 2003), (VELILLA; VALENCIA; MORENO, 2008), dentre outros.
O método simplex só pode ser utilizado na solução de problemas de programação linear se o problema estiver escrito em formato padrão, ou seja,
max/min z = cx
Sujeito as restrições
Ax = b
x ≥ 0
b ≥ 0
Para converter uma inequação em uma equação poderão ser utilizados dois tipos de variáveis:
As características para o sistema linear de equações são(PLOSKAS; SAMARAS, 2014):
Se a função objetivo possui um máximo (ou mínimo) finito, então pelo menos uma solução ótima é um ponto extremo do conjunto convexo C do Teorema 1.
Se a função objetivo assume um máximo (ou mínimo) em mais de um ponto extremo, então ele assume o mesmo valor para qualquer combinação convexa desses pontos extremos.
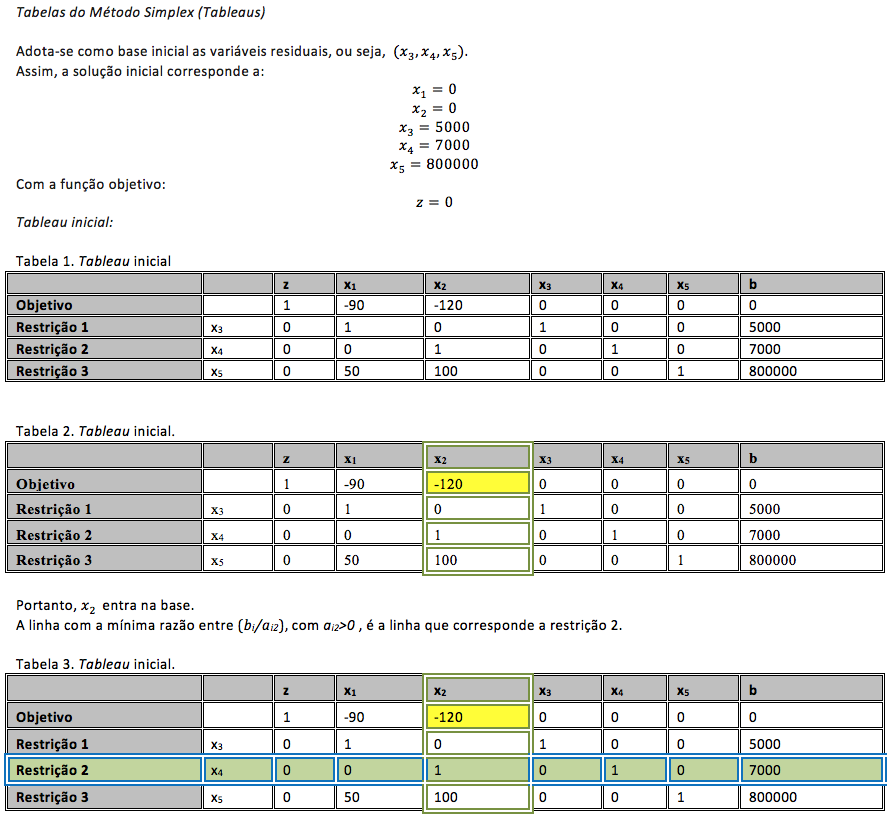
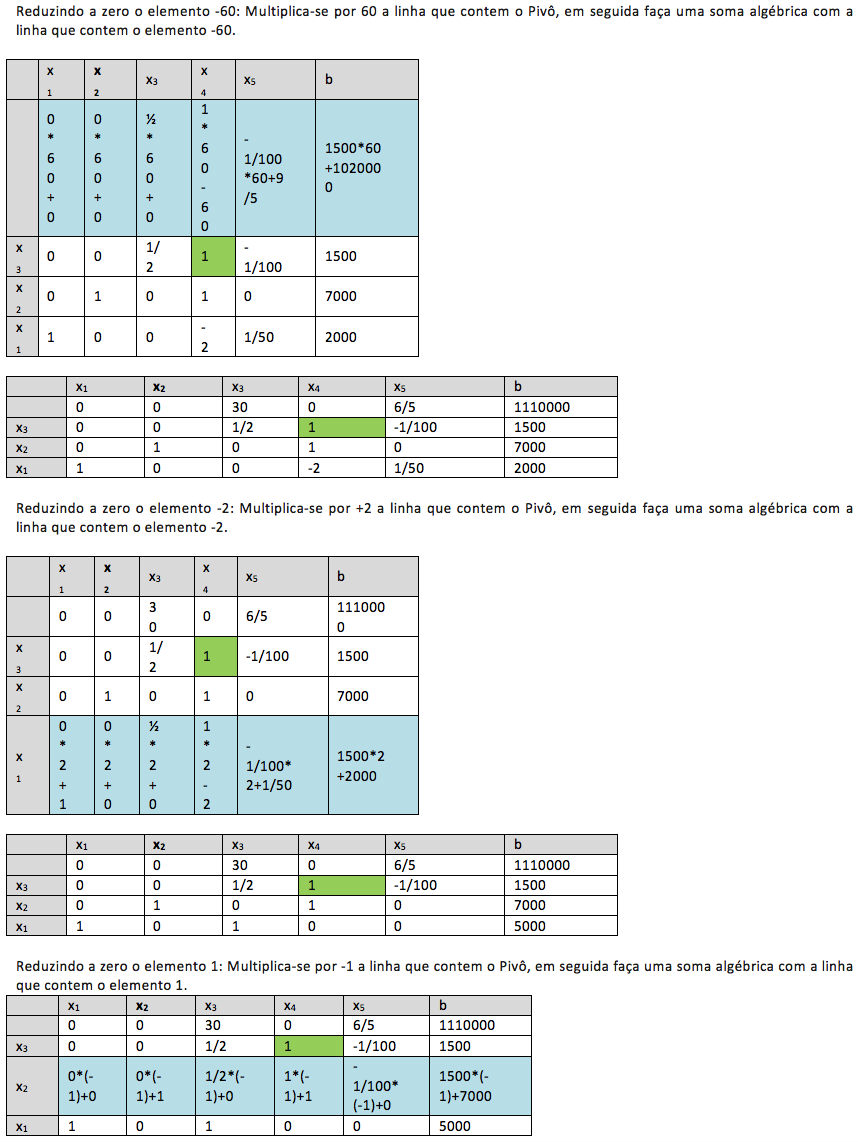
Os Passos do Método Simplex, sabe-se que a solução ótima do modelo é uma solução básica do sistema, ou seja, um ponto extremo do polígono gerado pelas restrições. Para iniciarmos o Método Simplex necessita-se de uma solução básica viável inicial, a qual é um dos pontos extremos. Este método verifica se a presente solução é ótima. Se esta não for é porque um dos demais pontos extremos adjacentes (vértices) fornecem valor menor para a função objetivo que a atual, quando o problema considerado é de minimização. Ele então faz uma mudança de vértice na direção que mais diminua a função objetivo e verifica se este novo vértice é ótimo. O processo termina quando, estando num ponto extremo, todos os outros pontos extremos adjacentes fornecem valores maiores para a função objetivo.
Portanto, a troca de vértice, faz uma variável não básica crescer (assumir valor positivo) ao mesmo tempo em que zera uma variável básica (para possibilitar a troca) conservando a viabilidade do Problema de Programação Linear.
Para isso, escolhemos uma variável cujo custo relativo é mais negativo (não é regra geral) para entrar na base e as trocas de vértices são feitas até que não exista mais nenhum custo relativo negativo.
A variável que sairá da base é aquela que, ao se anular, garante que as demais continuem maiores ou iguais a zero quando aumentamos o valor da variável que entra na base (respeitando a factibilidade).
O Método Simplex compreenderá, portanto, os seguintes passos:
i. Achar uma solução factível básica inicial.
ii. Verificar se a solução atual é ótima. Se for, pare. Caso contrário, siga para o passo iii.
iii. Determinar a variável não básica que deve entrar na base;
iv. Determinar a variável básica que deve sair da base;
v. Atualizar o sistema à fim de determinar a nova solução factível básica, e voltar ao passo ii.
A figura 1 a seguir é utilizado para problemas de minimização. Para problemas de maximização, este quadro pode ser usado, desde que os elementos da linha inferior sejam colocados com sinal invertido. Uma vez obtida esta ultima linha do Quadro, a segunda linha e a segunda coluna do Quadro, correspondentes a CT e C0, respectivamente, tornam-se supérfluas e podem ser eliminadas (MOLITERNO, 2016).

De forma a elucidar o passo a passo de solução de um problema de programação linear, selecionamos o exemplo dado por (KAGAN N. ET AL, 2009). Este consiste de:
"Um produtor independente dispõe de 2 unidades de geração, que podem ser conectadas ao sistema elétrico em pontos distintos, para a venda do excedente de energia elétrica que são capazes de produzir. Tanto os custos de produção quanto as tarifas negociadas para a venda de energia são distintos para os 2 geradores. O produtor deseja vender o máximo possível de energia seguindo, entretanto, seu plano de negócios, que não permite gastar acima de um valor pré-estabelecido para a produção de energia."
Dados do problema:






O Software OTIMIZA (KAGAN N. ET AL, 2009) é um software didático com aplicação de técnicas de otimização a problemas de engenharia de potência.

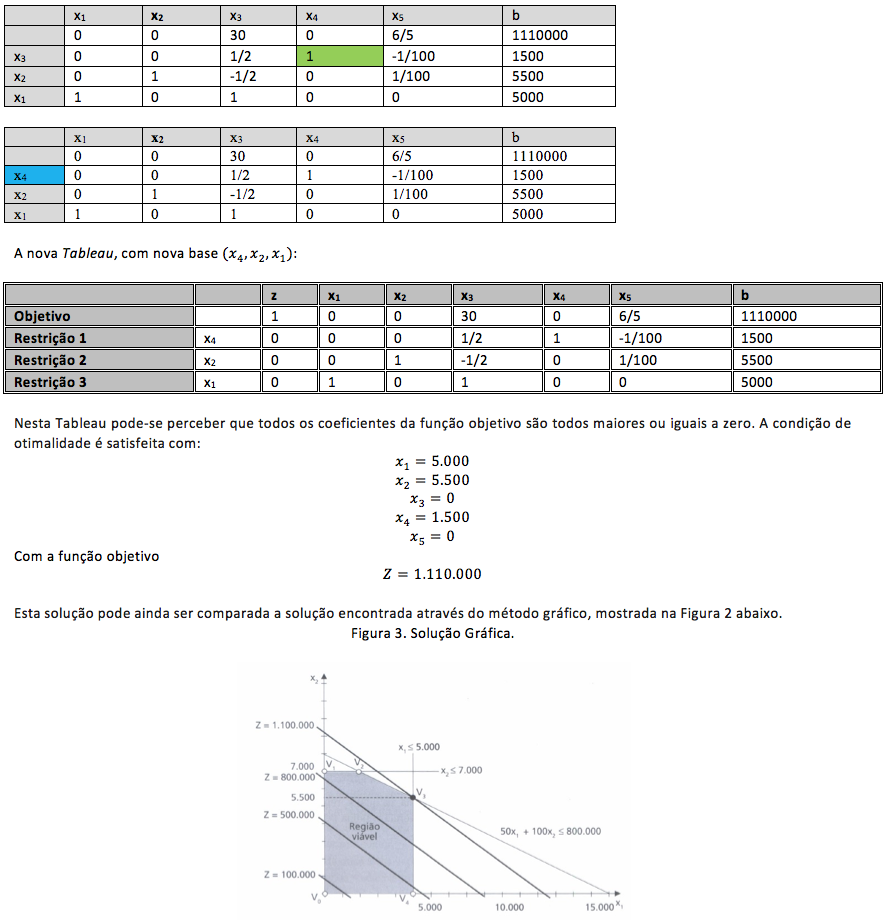
Neste artigo fizemos uma breve explanação sobre o Método Simplex e realizamos uma aplicação detalhada do procedimento de cálculo usando este método.
A maior contribuição deste artigo está na forma detalhada como o problema é resolvido, visto que não existem na literatura tais contribuições. Existem apenas passo-a-passos que não explicam de forma completa como obter a solução do problema de programação linear através do método Simplex.
É importante ressaltar ainda que as soluções encontradas através do método Simplex correspondem exatamente aos vértices Vo, V1, V2 e V3 encontrados através do método gráfico, Figura 2.
DANTZIG, G. B.; THAPA, M. N. Linear Programming: 2: Theory and Extensions. Nova York: [s.n.].
DAVOODI, E.; HAGH, M. T.; ZADEH, S. G. A hybrid Improved Quantum-behaved Particle Swarm Optimization – Simplex method ( IQPSOS ) to solve power system load flow problems. Applied Soft Computing Journal, v. 21, p. 171–179, 2014.
KAGAN N. ET AL. Métodos de Otimização Aplicados a Sistemas Elétricos de Potência. São Paulo: [s.n.].
MOLITERNO, C. MÉTODO SIMPLEX. Disponível em: <http://www.celiomoliterno.eng.br/Arquivos/Pesop/Metodo Simplex.pdf>. Acesso em: 5 maio. 2016.
NASH, J. C. THE (DANTZIG) SIMFLEX METHOD FOR LINEAR PROGRAMM. Computing in Science & Engineering, v. 2, n. 1, p. 29–31, 2000.
NEZAMABADI, H.; VAHIDINASAB, V. Two stage decision making of technical virtual power plants in electricity market via Nash-SFE equilibrium. 2015 3rd International Istanbul Smart Grid Congress and Fair, ICSG 2015, 2015.
PLOSKAS, N.; SAMARAS, N. The Journal of Systems and Software GPU accelerated pivoting rules for the simplex algorithm. The Journal of Systems & Software, v. 96, p. 1–9, 2014.
PLOSKAS, N.; SAMARAS, N. Efficient GPU-based implementations of simplex type algorithms. APPLIED MATHEMATICS AND COMPUTATION, v. 250, p. 552–570, 2015.
SAN, R. E. N. Z.; CHEN, Y. Hybrid Simplex-improved Genetic Algorithm for Global Numerical Optimization. ACTA Automatica SInica, v. 33, n. 1, 2007.
SOUSA, R. S. Métodos tipo dual simplex para problemas de otimização linear canalizados *. Tese doutorado Instituto de Ciências Matemáticas e de Computação - ICMC-USP, p. 168, 2005.
TAN, K. K.; CHIN, S. J.; DOU, H. F. Feedforward suppression of force ripple based on a simplex-optimized dither signal. p. 19–27, 2003.
VELILLA, E.; VALENCIA, J. A.; MORENO, G. “Using genetic algorithm and the simplex method to obtain equivalent circuits of the grounding systems”. IEEE/PES Transmission and Distribution Conference and Exposition: Latin America, p. 1–5, 2008.
YAMAMURA, K.; KITAKAWA, T. “Finding all solutions of piecewise-linear resistive circuits using the simplex method”. Circuits and Systems 2003. ISCAS ’03. Proceedings of the 2003 International Symposium on, v. 3, p. III–III, 2003.
1. Universidade Federal de Santa Maria (UFSM), Santa Maria, Rio Grande do Sul, Brasil, mbmansilha@gmail.com
2. Universidade Federal de Santa Maria (UFSM), Santa Maria, Rio Grande do Sul, Brasil, fafarret@gmail.com
3. Universidade Federal de Santa Maria (UFSM), Santa Maria, Rio Grande do Sul, Brasil, deise@gedre.ufsm.br