

Vol. 38 (Nº 58) Año 2017. Pág. 25
Jose NOGUERA Polania 1; Olmer GARCÍA Bedoya 2; Carlos ROBLES Algarin 3
Recibido: 03/08/2017 • Aprobado: 01/09/2017
RESUMEN: Se presenta el diseño de un control estándar basado en la norma H2 y de un control H-infinito aplicados en un manipulador de dos grados de libertad. El manipulador se modeló con las ecuaciones de Euler-Lagrange y la función de disipación de Rayleigh. Se utilizó un modelo en el Toolbox SimMechanics exportando la geometría y propiedades físicas desde SolidWorks. Los resultados demuestran que la respuesta transitoria en el control H infinito es más suave que en el control estándar. |
ABSTRACT: This paper presents the design of a standard control based on the H2 standard and an H-infinity control applied in a manipulator of two degrees of freedom. The manipulator was modeled with the Euler-Lagrange equations and the Rayleigh dissipation function. A model was used in the SimMechanics Toolbox by exporting geometry and physical properties from SolidWorks. The results obtained show that transient response in H infinity control is smoother than the standard control. |
Los robots industriales son dispositivos mecánicos multifuncionales programables, diseñados para mover materiales, piezas, herramientas, entre otro tipo de elementos (Craig, 2006). En el sector industrial se emplean estos sistemas robóticos para el desarrollo de tareas que típicamente son peligrosas, inseguras, altamente repetitivas o no placenteras para el ser humano (Robles, Román, & Polo, 2016). Han tenido diversas aplicaciones tales como manejo de materiales, ensamble, soldadura, pintura y fumigación.
Dado que cada vez es necesario mayor exactitud y precisión en estos dispositivos, en este artículo se presentan dos técnicas de control Robusto: control estándar y control H infinito (H∞). El control estándar es una metodología de control basada en la minimización de la norma H2 sobre la representación en variables de estado (De Larminat, 2000). El método se desarrolla por medio de una estimación de los estados del proceso y de los estados de un modelo del entorno como las perturbaciones y las señales de referencia.
El control H∞ consiste en la minimización de una determinada función de costo formulada en el dominio del tiempo a partir de ciertas especificaciones de diseño (Rodríguez & López, 1996). Una medida para la minimización de esta función de costo empleada en los problemas de control óptimo y robusto es la norma H∞. En esta técnica se obtiene un controlador de la misma dimensión de la planta ampliada. Este modelo es determinado por el sistema y un conjunto de filtros que permiten cumplir con los parámetros de diseño en ciertos rangos de frecuencia (Rigatos, Siano, & Raffo, 2016).
El modelo del robot manipulador a controlar posee dos grados de libertad y dadas las características no lineales el diseño de los controladores se realiza bajo el modelo linealizado sobre un punto de operación (Appala & Ghosal, 2015). El brazo articulado es realizado en la herramienta de diseño asistido CAD (Computer Aided Design) Solidworks y exportado al Toolbox de Matlab SimMechanics para realizar las simulaciones de los controladores (Chikhi, Amine, Chaoui, & Khireddine, 2016).
La organización del artículo inicia con la descripción del modelado matemático del brazo manipulador a través de las ecuaciones de movimiento de Euler-Lagrange (Feynman, 1999) y de la función de disipación de Rayleigh (Minguzzi, 2015), (Genta, 2009). Luego, se evalúa el modelo en SimMechanics Simulink según los datos exportados de SolidWorks. Posteriormente, se describe la teoría de control estándar y H∞. Finalmente, se presentan los resultados de los controladores en Simulink y las conclusiones.
Para la obtención del modelo matemático de la Figura 1, se simplificó el sistema por medio de una masa ubicada en el centro de cada eslabón y una masa puntual al final del eslabón dos que representa la carga del manipulador.
Figura 1
Esquema del sistema modelado en SolidWorks.

El primer paso para la obtención del modelo dinámico es conocer la ubicación de las masas, con respecto al origen ri, que componen el sistema; como se puede observar en las Ecuaciones 1, 2 y 3.


Figura 2
Valores de torque estático del sistema.

El modelo CAD desarrollado en SolidWorks como se observa en la Figura 1 se exporta al Toolbox de Simulink-SimMechanics (Danek, Turevskiy, & Denery, 2007). La exportación consiste en las propiedades de los cuerpos rígidos como son la matriz de momentos de inercia, la masa y los vectores necesarios para representar cada uno de los objetos. La exportación obtenida se observa en la Figura 3.
Figura 3
Modelo en Simulink del manipulador.

Para obtener el modelo completo sobre el cual se simulan los controladores, se requiere adicionar sensores en cada una de las articulaciones que transforman a variables de Simulink la información de interés como lo son para el caso particular, posiciones y velocidades angulares de cada eslabón. Por otro lado, se conectan actuadores permitiendo enviar variables de Simulink a SimMechanics. Una vez realizado esto se simula el rozamiento multiplicando la velocidad angular de cada articulación por un factor vi que hace referencia al coeficiente de rozamiento, el resultado se resta al torque de entrada Ti.
El control estándar se basa en la norma H2, donde se emplean los algoritmos LQG (Linear Quadratic Gaussian). La dificultad en la implementación del control radica en la definición de la función a minimizar. Esta función se obtiene a partir de la construcción de un modelo de control estándar. El modelo incluye las dinámicas del proceso y la información sobre su entorno y objetivos de control (De Larminat, 2000), (De Larminat, 2007).
Como se mencionó antes, dado el problema de optimización H2, la cuestión es encontrar un valor K de acuerdo a la Ecuación 13.

Figura 4
Diagrama del control Estándar.





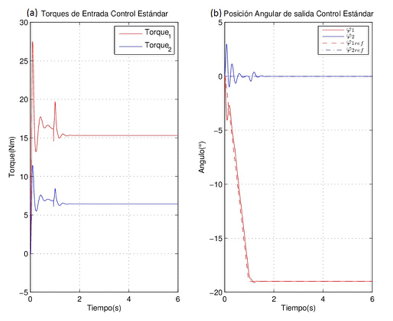
Figura 5
Respuesta del controlador diseñado por la técnica de control estándar.
El controlador obtenido se simula con la planta no lineal como se puede observar en la Figura 6. Los resultados obtenidos con el controlador diseñado por la técnica de control H∞ a una referencia dada planteada a partir de un perfil de velocidad se evidencian en la Figura 7. Específicamente, en la Figura 7.a se observa que la señal de control es más suave que la obtenida por el control estándar. La respuesta del sistema en lazo cerrado, Figura 7.b, ante una señal de referencia con una trayectoria trapezoidal de ϕ1 presenta un bajo sobrepaso, puesto que el sistema de control se desarrolló para obtener una mejor estabilidad sobre la planta.
Figura 6
Modelo en Simulink del controlador H∞.

------
Figura 7
Respuesta del sistema con el controlador diseñado por la técnica de control H∞.

1. La exportación de modelos de CAD a Simulink, genera una ventaja para los dos programas, pues esto permite realizar un proceso de diseño de controladores mucho más aproximado y para el CAD puede servir para tomar estos resultados de las señales de control para analizar por medio de elementos finitos los esfuerzos en las piezas.
2. El diseño de controladores estándar que minimizan la norma H2 como el realizado en este artículo tienen la cualidad de ser fácilmente sintonizables al solo depender de dos parámetros y adicionalmente al permitir incluir en el modelo las perturbaciones que rodean el sistema como en este caso que fueron los puntos de operación.
3. Es preciso tener en cuenta que el valor de sintonización T0 debe ser generalmente mayor que Tc dado que este fijará los modos dominantes de control
4. El diseño de controladores H∞ permite relacionar muy fácilmente los parámetros de diseño frecuenciales en el controlador. Esto se realiza por medio de un correcto diseño de los filtros y un adecuado entendimiento de los requerimientos de robustez y sensibilidad requeridos.
5. Como comparación entre el controlador H∞ y el control estándar implementado se encontró que el primero tiene un error en estado estable que el segundo no tiene. La respuesta transitoria en el control H∞ es mucho más suave que en el control estándar.
ABDALÁ, S., & Ñeco, R. (2003). Caracterización de un Robot Manipulador Articulado. Tesis de Maestria. Cuernavaca, México: Cenidet.
APPALA, T., & Ghosal, A. (2015). A mobile robot with a two-degree-of-freedom suspension for traversing uneven terrain with minimal slip: Modeling, simulation and experiments. Mechanism and Machine Theory, 93, 83-97.
CHIKHI, S., Amine, A., Chaoui, A., & Khireddine, M. E. (2016). Modelling and Implementation of Complex Systems. Constantine: Springer.
CRAIG, J. (2006). Robótica. México DF: Prentice Hall.
DANEK, J., Turevskiy, A., & Denery, T. (2007). Simulation and Animation of Mechanical Systems. AIAA Modeling and Simulation Technologies Conference and Exhibit, Guidance, Navigation, and Control and Co-located Conferences, 1-10.
DE LARMINAT, P. (2000). Contrôle d'état standard. Paris: Hermès science publications.
DE LARMINAT, P. (2007). Analysis and Control of Linear Systems. Nantes: Wiley.
FEYNMAN, R. (1999). Fisica Volumen 2 - Electromagnetismo y y Materia. Massachusetts: Addison Wesley Longman.
GENTA, G. (2009). Vibration Dynamics and Control. New York: Springer.
MACIEJOWSKI, J. (1989). Multivariable Feedback Design. Padstow: Addison-Wesley.
MINGUZZI, E. (2015). Rayleigh's dissipation function at work. European Journal of Physics, 36(3), 14-35.
RIGATOS, G., Siano, P., & Raffo, G. (2016). An H-infinity nonlinear control approach for multi-DOF robotic manipulators. IFAC-PapersOnLine, 49(12), 1406-1411.
ROBLES, C., Román, D., & Polo, A. (2016). Brazo robótico con dieciocho grados de libertad tele-operado por un guante electrónico. Revista Espacios, 38(3), 22.
RODRÍGUEZ, F., & López, M. (1996). Control adaptativo y robusto. Sevilla: Universidad de Sevilla.
SHUKLA, P., Ghodki, D., Suresh, N., & Singru, P. (2016). A Study of H infinity and H2 synthesis for Active Vibration Control. IFAC-PapersOnLine, 49(1), 623-628.
1. Magíster en Ingeniería. Profesor Catedrático y Estudiante de Doctorado en Ingeniería, Departamento de Ingeniería Mecánica, Universidad del Norte. Email: jfnoguera@uninorte.edu.co
2. Doctor en Ingeniería. Profesor Tiempo Completo, Departamento de Ingeniería, Universidad Jorge Tadeo Lozano Bogotá. Email: olmer.garciab@utadeo.edu.co
3. Doctor en Ciencias. Profesor Tiempo Completo, Facultad de Ingeniería, Universidad del Magdalena. Email: carlosarturo.ing@gmail.com