

 Vol. 38 (Nº 55) Año 2017. Pág. 17
Vol. 38 (Nº 55) Año 2017. Pág. 17
Blanca CUJI 1; Wilma GAVILANES 2; Rina SANCHEZ 3
Recibido: 24/07/2017 • Aprobado: 20/08/2017
RESUMEN: Este artículo muestra la construcción de un modelo predictivo de deserción estudiantil, para pronosticar la probabilidad, que un estudiante abandone su programa académico, mediante técnicas de clasificación, basadas en árboles de decisión. La metodología utilizada, se basa en Knowledge Discovery in Database (KDD), con cinco etapas: selección, procesamiento, transformación, minería de datos y evaluación. Aplicando el algoritmo, Classification and Regression Tree (CART) de la herramienta R, se construyó un árbol con cuatro niveles de profundidad y mismo número reglas, que evalúan a los posibles desertores. Llevando a concluir que las variables nivel y notas tienen mayor influencia en la deserción. |
ABSTRACT: This article presents the construction of a predictive model of student desertion, to predict the probability of a student dropping out of their academic program, using classification techniques based on decision trees. The methodology used is based on Knowledge Discovery in Database (KDD), which consists of five stages: selection, processing, transformation, data mining and evaluation. Applying the algorithm, Classification and Regression Tree (CART) of the statistical software R, a tree with four levels of depth and the same number of rules were constructed, which evaluate possible deserters. It was found that the variables level and notes have a greater influence on students' dropout rates. |
El alto nivel de deserción estudiantil, es uno de los problemas principales que enfrentan las instituciones de educación superior de América Latina y el Caribe. Se estima, que la tasa de deserción anual, está en el orden del 57%, Claudio (2007), según el informe emitido por la Organización de las Naciones Unidas para la Educación la Ciencia y la Cultura (UNESCO). En un periodo de tiempo normal, solamente logran graduarse, alrededor del 43% de los que ingresan en cada carrera (Sánchez, 2015).
Cada día, las instituciones de educación superior, generan gran cantidad de datos personales, académicos, socioeconómicos de los estudiantes (Amaya, Barrientos, & Heredia, 2015). La aplicación de técnicas de minería de datos permite, entre otras cosas, predecir cualquier fenómeno, con un porcentaje alto de confiabilidad (Timar & Jim, 2015). De esta forma, se puede pronosticar, la probabilidad de deserción de un estudiante, basado en los datos históricos, almacenados en los sistemas de información (Spositto & Etcheverry, 2010), de las instituciones.
Estudios previos, muestran la generación de modelos predictivos de deserción, basados en arboles de decisión, aplicando algoritmos como: EquipAsso (Basado en operadores algebraicos), J48 (Timar & Jim, 2013), C4.5 (Salazar, Gosalbez, Bosch, Miralles, & Vergara, 2004), ID3 (Gandhi & T.Archana, 2016), ADTree (Marquez-Vera, 2013), CART (Ara, Halland, Igel, & Alstrup, 2015). Sin embargo otros modelos utilizan técnicas como: redes bayesianas, regresión logística (Dunn & Mulvenon, 2009), redes neuronales (Sveučilište u Splitu. Ekonomski fakultet., Garača, & Čukušić, 2010). Para el caso que nos ocupa, se usó la técnica de clasificación basada en arboles de decisión conjuntamente con el algoritmo CART, por contar con la población y el número de variables estimadas para su aplicación.
El objetivo de este estudio fue crear un modelo predictivo de deserción estudiantil, para determinar la probabilidad, que un estudiante abandone la universidad, teniendo en cuenta, el rendimiento académico y variables de su entorno personal.
El documento está estructurado de la siguiente manera: En primer lugar, se presenta un breve resumen, de los trabajos relacionados a la creación de modelos predictivos de deserción estudiantil, con técnicas de clasificación basadas en arboles de decisión, los algoritmos y las herramientas utilizadas. Luego, se describe la metodología utilizada para la generación del modelo predictivo, KDD, con cinco etapas: selección, procesamiento, transformación, minería de datos y evaluación. Posteriormente, se presenta los resultados de la creación del modelo y su aplicación.
Finalmente, se expone las conclusiones, sobre la aplicación del modelo predictivo.
El estudio comparativo de algoritmos para predecir la deserción, utiliza información personal y académica de los estudiantes. Los autores (Hernandez Gonzalez et al., 2016), desarrollaron un sistema predictivo para detectar al alumno con probabilidad de deserción. Utilizando la herramienta, Microsoft SQL Server Analysis Services, se crea un modelo de predicción de atributos discretos y continuos, utilizando un algoritmo de clasificación y regresión, para encontrar los estudiantes con elevado porcentaje de deserción mediante un árbol de decisión.
Los autores (Romero Morales, Cristóbal; Márquez Vera, Carlos; Ventura Soto, 2012) emplean, la técnica de clasificación basada en árboles de decisión para predecir, a estudiantes que pueden abandonar sus estudios. Usan variables como: semestre que cursan, estado civil, discapacidad física, nivel económico, edad, sexo, trabajo del padre y la madre, notas de los exámenes entre otros. A partir de los árboles generados, por los algoritmos ADTree y SimpleCart de la herramienta Waikato Environment for Knowledge Analysis (WEKA), se obtienen reglas, que alerta al profesor, sobre los estudiantes que se encuentren en riesgo de suspender o abandonar sus estudios.
Por otro lado, se propone, la construcción de un modelo predictivo de rendimiento académico, con datos de 932 estudiantes, en dos etapas: La primera, se refiere a la extracción y preparación de la información a través de la limpieza y estructuración de datos. La segunda, constituye la aplicación de minería de datos, por medio de actividades de carga y procesamiento, así también la formulación del modelo e interpretación de resultados (Merchán & Duarte, 2016). Para el proceso de minería de datos se utiliza WEKA, que genera un árbol de decisión basado en el algoritmo J48.
La extracción de perfiles de deserción estudiantil, a partir de datos socioeconómicos y académicos, obtiene patrones de deserción estudiantil (Timar & Jim, 2015), basado en el promedio de calificaciones y materias perdidas en los primeros semestres de la carrera. Se utiliza, MS SQL Server para la generación del almacén de datos, SPSS para el pre-procesamiento de la información y WEKA para encontrar un clasificador de rendimiento académico y detectar los patrones determinantes de la deserción estudiantil.
El proceso de modelamiento de un árbol de decisión, comienza, identificando los factores que influyen en la deserción. Para (Khalilian, Mustapha, Sulaiman, & Mamat, 2011), estos factores se centran en variables como: ingreso económico y educación de los padres, número de hijos, estado civil, rendimiento académico entre otros. Se construye un árbol de decisión de cuatro niveles de profundidad, usando el algoritmo J4.8, con la herramienta WEKA. Se identifican las variables ingresos económicos de los padres, nivel previo al semestre y asistencia, como aquellas que mayor incidencia tienen en la deserción.
Un árbol de decisión es un diagrama que contiene: Un nodo raíz donde se encuentran todas las observaciones; nodos internos que albergan a los nodos de división y los nodos hoja que contiene la clasificación final para un conjunto de observaciones (Khalilian et al., 2011). Los arboles de decisión son parte de las técnicas de minería de datos (Márquez-Vera, Cano, Romero, & Ventura, 2013). Un árbol representa una segmentación de los datos, que se crea mediante la aplicación, de una serie de reglas simples (Marquez-Vera, 2013). Cada regla asigna una observación, a un segmento basada en el valor de una entrada. Una regla se aplica después de otra, dando como resultado una jerarquía de segmentos dentro de segmentos. La jerarquía se llama árbol y cada segmento se llama nodo (Romero Morales, Cristóbal; Márquez Vera, Carlos; Ventura Soto, 2012). Así, los nodos internos de un árbol representan validaciones sobre los atributos, las ramas representan las salidas de las validaciones, y los “nodos hoja” representan las clases (Karina, Torrado, Barrientos Avendaño, Judith, & Vizcaíno, n.d.).
El algoritmo CART de Leo Breiman (Alcover, R., Benlloch, J., Blesa, P., Calduch, M. A., Celma, M., Ferri, C., & Robles, 2007), realiza particiones binarias, con el objetivo que la media de cada rama sea diferente y, por tanto, discrimine con suficiente precisión, un número adecuado de particiones, para asignar a cada hoja un valor cercano a la media de los elementos que caen en ella. Este algoritmo genera arboles de fácil interpretación con resultados óptimos (Ara et al., 2015), lo que se considera una ventaja, al crear modelos predictivos (Lin, 2015).
La metodología aplicada de basa en el Proceso KDD, con cinco etapas: selección, procesamiento, transformación, minería de datos y evaluación.
Figura 1. Proceso de selección de datos
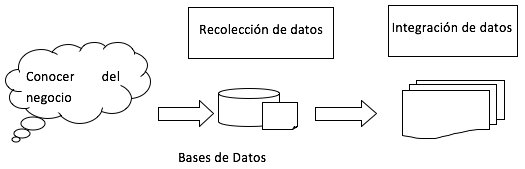
Recolección de datos
Los datos, corresponden a los estudiantes de la Carrera Docencia en Informática de la Universidad Técnica de Ambato (UTA). La Dirección de Tecnología de la Información y Comunicación (DITIC) de la institución proporcionó, la información a partir del año 2006, en dos matrices. La Matriz 1 contiene, los datos personales con los atributos: identificación, que fue reemplazado, por un identificador numérico del 1...n, para mantener la confidencialidad de los participantes, según lo expone la Ley del Sistema Nacional de Registro de Datos Públicos (Nacional Pleno, n.d.). Además, género, estado civil, etnia, fecha de nacimiento, lugar nacimiento, ciudad de residencia (ver Figura 2). La matriz 2 contiene datos académicos con atributos relacionados al periodo académico, curso matriculado, materia, promedio de notas obtenidas en el primer parcial (nota1) y segundo parcial (nota2) (ver Figura 3).
Figura 2. Matriz 1: Datos generales.

-----
Figura 3. Matriz 2: Datos académicos.

Inicialmente se contó con 484 registros para el análisis. Los atributos de la matriz 1 y matriz 2, fueron integrados en una hoja de cálculo, además se agregó, edad, desertor, nota1, nota2 con prefijos que representan los niveles alcanzados por el estudiante (p=primero, s=segundo, t=tercero, c=cuarto, q=quinto, e=sexto) (ver Figura 4).
Figura 4. Matriz integral: unificación de la matriz 1 y 2, con atributos
como edad, nota1 y 2 por niveles, atributo desertor.

Los atributos edad, desertor, nota1p, nota2p...n, se determinaron de la siguiente manera:
Edad: Fecha de nacimiento menos la fecha de ingreso a la carrera.
Desertor: Este atributo se determinó en base al curso matriculado y notas por materia que constan en los datos históricos del estudiante.
nota1p, nota2p, nota2s, nota2s...n: Promedio de notas por materia, tomadas por el estudiante, en el primero y segundo parcial (nota1p, nota2p), de todos los niveles alcanzados.
Figura 5. Etapas para el procesamiento de datos.
Se detectó datos atípicos (observaciones extremadamente grandes o pequeñas, que dista del resto de valores, Pérez (2007), utilizando el programa FactorMiner de R; con diagramas de pareto, para las variables: edad (ver Figura 6), nota1p, nota2p, nota2s, nota2s. Se encontraron 10 datos atípicos, para el atributo edad. Tres estudiantes tienen 41 años, mientras que existe un estudiante con 40, 34, 33, 32, 31, 30 y 25 años.
Boxplot ( edad = 41, 41, 41, 40, 34, 33, 32, 31, 30, 25).
Figura 6. Datos atípicos del atributo edad
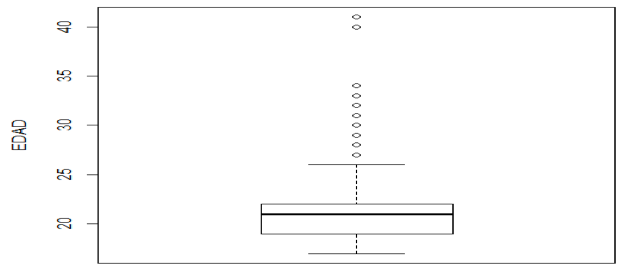
Se ha modificado la salida original del Boxplot, para identificar registros, donde no se encontraron notas (s/n= sin nota)
Boxplot( nota1p = 0.0, s/n, 0.0, s/n, 0.0, 0.0, 0.0, 0.0, 0.0,0.0 )
Boxplot(nota2p =0.0, 0.0,s/n,0.0,0.0,0.0, 0.0, s/n, 0.0, 0.0, 10.0, 10.0, 10.0)
Boxplot(nota1s= s/n, s/n, s/n, 0.0,s/n, s/n, s/n, s/n, s/n, s/n)
Boxplot(nota2s=s/n, 0.0, s/n, s/n, s/n,0.0, s/n,0.0, s/n, s/n)
Se eliminó de la base de datos, a 24 estudiantes que mostraron atipicidades, en las variables, edad, nota1p, nota2p, nota2s, nota2s, cuyo valor fue s/n, 0.0, y 10.0. Además se reemplazó, los caracteres especiales como la ñ y tildes, en el atributo nombre, lugar de nacimiento y ciudad de residencia, para evitar resultados erróneos. De igual manera, a ocho estudiantes, por no contar con notas en ningún nivel.
Se obtuvo una base de datos limpia con 425 estudiantes, almacenada en una hoja de cálculo.
Figura 7. Etapas para la transformación de datos

Se tomó datos, de 485 estudiantes, almacenados en hojas de cálculo y base de datos relacionales, de la DITIC. Los datos fueron transformados, a variables, según los tipos de atributos propuestos por el estadístico S. Stevens (1946), se clasificaron en tres tipos: nominal, ordinal y cuantitativo, según Tabla 1.
Tabla 1. Variables predictoras
Atributos |
Tipo de atributo S. Stevens (1946) |
Genero |
Nominal |
Estado Civil |
Nominal |
Etnia |
Nominal |
Edad |
Cuantitativo |
Lugar de Nacimiento |
Nominal |
Ciudad de residencia |
Nominal |
Nivel |
Ordinal |
Nota1p |
Cuantitativo |
Nota2p |
Cuantitativo |
Fuente: Elaboración propia
-----
Tabla 2. Variable a predecir
Atributos |
Tipo de atributo S. Stevens (1946) |
Desertor |
Nominal |
Fuente: Elaboración propia
Durante el análisis de la literatura, se detectó variables como: discapacidad física, trabajo del padre y de la madre, entre otras (Romero Morales, Cristóbal; Márquez Vera, Carlos; Ventura Soto, 2012), que no formaron parte del estudio, por la ausencia de datos.
Figura 8
Etapa de minería de datos

El proceso, para la generación del modelo predictivo en sus diferentes fases (ver Figura 9):
Figura 9
Esquema para la generación del modelo predictivo de deserción estudiantil

Se usó árboles de decisión, conjuntamente con el algoritmo CART de la herramienta Rattle de R. Este algoritmo utiliza, el proceso “Top-Down” (algoritmo Hunt) para construir, el árbol de arriba hacia abajo. Se utilizó, este algoritmo por contar con variables nominales y cuantitativas. Además, el número de variables es apropiado para su aplicación.
Para la generación del modelo predictivo, se usó Rattle de R; se construyó un árbol con cuatro niveles de profundidad y mismo número de reglas, tomando como variable predictora a “Desertor”, de tipo nominal (ver Figura 10).
Figura 10. Árbol de decisión, generado con Rattle de R.

Para la construcción del modelo, se tomó el 90% de los datos, para la tabla de aprendizaje y el 10% para la tabla de pruebas.
Para la evaluación del modelo, se construyó la curva Receiver Operating Characteristic (ROC) para medir su efectividad (ver Figura 11).
Figura 11. Evaluación del modelo, predicción al 94% de efectividad

La curva ROC, muestra al modelo con un 94% de efectividad en la predicción.
Para probar el modelo, se utilizaron, los datos de la tabla de pruebas, mostrando los siguientes resultados (ver Figura 12).
Figura 12. Historial de cálculos.

Adicionalmente durante la etapa de integración de datos, se logró determinar los siguientes resultados:
Tabla 3. Deserción
Desertor |
Número de estudiantes |
Porcentaje |
Si |
132 |
35% |
No |
246 |
65% |
Total |
378 |
100% |
Fuente: Elaboración propia
El 35% de la población estudiada, ha desertado.
El estudio incluyo seis variables, socioeconómicas y cinco académicas. Los resulta-dos del análisis encontraron que la prioridad de estas variables estaba en el nivel, edad, nota1s, nota2s. El género, estado civil, etnia, lugar de nacimiento, ciudad de residencia, nota1p y nota2p, no fueron incluidos en el modelo. El modelo presentó una probabilidad de certeza el 94%. El resultado de la evaluación, presenta al modelo como estable y aceptable.
Los resultados del análisis del árbol de decisión, encontraron que la profundidad de la estructura del árbol era de cuatro niveles de profundidad. El primer nodo se formó con la variable nivel (decimo, noveno, octavo, séptimo, y sexto). El Segundo nodo se formó con la variable nota1s, el tercero con la variable nota2s y el cuarto nivel, con la variable nivel y nota1s.
De las 11 variables que de utilizaron para la construcción del modelo, la variable nivel, es aquella que mayor incide en la deserción, así: mayor tendencia a desertar: primero, segundo, tercero, cuarto y quinto nivel, mínima tendencia: sexto, séptimo, y nula: octavo, noveno y décimo.
Los estudiantes que se encuentren en el nivel: decimo, noveno, octavo, séptimo, sexto y que tienen notas comprendidas entre (4.0, 4.5, 6.0, 6.3; 6.5, 6.6, 6.8, 6.9, 7.0, 7.1, 7.3, 7.5, 7.6, 7.7, 7.8, 8.0, 8.1, 8.2, 8.3, 8.4, 8.5, 8.6, 8.8, 8.9, 9.0, 9.2, 9.3, 9.4), no son desertores.
De los 485 estudiantes con 15475 registros analizados la variable edad y nota1s muestran mayor cantidad de datos atípicos.
Durante la creación del modelo, se descartaron las variables, genero, estado civil, etnia, lugar de nacimiento, ciudad de residencia, nota1p y nota2p.
Fue necesario realizar varias pruebas con el algoritmo CART, modificando continuamente, el porcentaje de datos asignados, para la tabla de aprendizaje y de pruebas, logrando obtener, mayor cantidad de nodos en el árbol.
El modelo propuesto abre oportunidades, para la creación de nuevos, modelos de predicción, usando técnicas de clasificación, más complejas como redes neuronales y regresión logística, que permitan un análisis comparativo, de los factores que in-fluyen en la deserción estudiantil.
Alcover, R., Benlloch, J., Blesa, P., Calduch, M. A., Celma, M., Ferri, C., & Robles, A. (2007). Análisis del rendimiento académico en los estudios de informática de la Universidad Politécnica de Valencia aplicando técnicas de minería de datos. Teruel, España., 169. Retrieved from http://bioinfo.uib.es/~joemiro/aenui/procJenui/Jen2007/alanal.pdf
Amaya, Y., Barrientos, E., & Heredia, D. (2015). Mining Techniques, 13(9), 3127–3134.
Ara, N.-B., Halland, R., Igel, C., & Alstrup, S. (2015). High-School Dropout Prediction Using Machine Learning: A Danish Large-scale Study. In ESANN 2015 proceedings, European Symposium on Artificial Neural Networks, Computational Intelligence and Machine Learning. (pp. 319–324). Retrieved from https://www.elen.ucl.ac.be/Proceedings/esann/esannpdf/es2015-86.pdf
Claudio, R. (2007). Informe sobre la Educación Superior en América Latina y el Caribe 2000-2005. Retrieved from http://www.oei.es/salactsi/informe_educacion_superiorAL2007.pdf
Dunn, K. E., & Mulvenon, S. W. (2009). A Critical Review of Research on Formative Assessments: The Limited Scientific Evidence of the Impact of Formative Assessments in Education. Practical Assessment, Research & Evaluation, 14(7), 1–11. https://doi.org/10.1002/ir
Gandhi, U. D., & T.Archana. (2016). Prediction of student performance in educational Data Mining - A Survey. International Journal of Pharmacy & Technology, 8(3), 17757–17763.
Hernandez Gonzalez, A. G., Melendez Armenta, R. A., Morales Rosales, L. A., Garcia Barrientos, A., Tecpanecatl Xihuitl, J. L., & Algredo, I. (2016). Comparative Study of Algorithms to Predict the Desertion in the Students at the ITSM-Mexico. IEEE Latin America Transactions, 14(11), 4573–4578. https://doi.org/10.1109/TLA.2016.7795831
Karina, Y., Torrado, A., Barrientos Avendaño, E., Judith, D., & Vizcaíno, H. (n.d.). Modelo predictivo de deserción estudiantil utilizando técnicas de minería de datos. Retrieved from http://documentos.redclara.net/bitstream/10786/759/1/124-22-3-2014-Modelo predictivo de deserción estudiantil utilizando técnicas de minería de datos.pdf
Khalilian, M., Mustapha, N., Sulaiman, M. N., & Mamat, A. (2011). Intrusion detection system with data mining approach: a review. Global Journal of Computer Science and Technology (Vol. 10). Global Journals. Retrieved from http://computerresearch.org/index.php/computer/article/view/891/890
Lin, S.-P. (2015). Using EDM for Developing EWS to Predict University Students Drop Out. International Journal of Intelligent Technologies and Applied Statistics, 8(4), 365–388. https://doi.org/10.6148/IJITAS.2015.0804.05
Marquez-Vera, C. (2013). Predicting school failure and dropout by using data mining techniques. … Del Aprendizaje, IEEE …, 8(1), 7–14. Retrieved from http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=6461622
Márquez-Vera, C., Cano, A., Romero, C., & Ventura, S. (2013). Predicting student failure at school using genetic programming and different data mining approaches with high dimensional and imbalanced data. Applied Intelligence, 38(3), 315–330. https://doi.org/10.1007/s10489-012-0374-8
Merchán, S. M., & Duarte, J. A. (2016). Analysis of Data Mining Techniques for Constructing a Predictive Model for Academic Performance. IEEE Latin America Transactions, 14(6), 2783–2788. https://doi.org/10.1109/TLA.2016.7555255
Nacional Pleno, A. EL. (n.d.). Ley del Sistema Nacional de Registro de Datos Públicos. Retrieved from https://www.telecomunicaciones.gob.ec/wp-content/uploads/downloads/2012/11/Ley-del-sistema-nacional-de-registro-de-datos-publicos.pdf
Pérez López, C., & Santín González, D. (2007). Minería de datos : técnicas y herramientas. Thomson. Retrieved from https://books.google.es/books?hl=es&lr=&id=wz-D_8uPFCEC&oi=fnd&pg=PR4&dq=datos+atipicos&ots=Th03ul1v4G&sig=N9j4nTVS09eayqtSUtAeGrSdR8w#v=onepage&q=datos atipicos&f=false
Romero Morales, Cristóbal; Márquez Vera, Carlos; Ventura Soto, S. (2012). Predicción del Fracaso Escolar Mediante Técnicas de Minería de Datos. Iee-Rita, 7(3), 109–117.
Salazar, A., Gosalbez, J., Bosch, I., Miralles, R., & Vergara, L. (2004). A case study of knowledge discovery on academic achievement, student desertion and student retention. ITRE 2004: 2nd International Conference Information Technology: Research and Education, Proceedings, (January 2016), 150–154. https://doi.org/Doi 10.1109/Itre.2004.1393665
Sánchez, D. (2015). La tendencia del abandono escolar en Ecuador: período 1994-2014. Revista Para La Docencia de Ciencias Económicas Y Administrativas En El Ecuador, 224. Retrieved from http://udla.edu.ec/cie/wp-content/uploads/2015/06/ValorAgregado03-Art.-2-Sánchez-Abandono-escolar.pdf
Spositto, O., & Etcheverry, M. (2010). Aplicación de técnicas de minería de datos para la evaluación del rendimiento académico y la deserción estudiantil Deserción. … En Sistemas, Cibernética E …. Retrieved from /citations?view_op=view_citation&continue=/scholar?hl=es&start=20&as_sdt=0,5&scilib=1024&citilm=1&citation_for_view=uOPNWhoAAAAJ:hNSvKAmkeYkC&hl=es&oi=p
Sveučilište u Splitu. Ekonomski fakultet., M., Garača, Ž., & Čukušić, M. (2010). Student dropout analysis with application of data mining methods. Management: Journal of Contemporary Management Issues, 15(1), 31–46. Retrieved from http://hrcak.srce.hr/53605
Timar, R., & Jim, J. (2013). Descubrimiento de perfiles de deserción estudiantil con técnicas de minería de datos. Revista Vínculos, 10(1), 373–383. Retrieved from http://revistas.udistrital.edu.co/ojs/index.php/vinculos/article/view/4687/6419
Timar, R., & Jim, J. (2015). Extracción de perfiles de deserción estudiantil en la institución universitaria cesmag 1, VI(1), 30–44.
1. Aspirante a Doctor en Ciencias Informáticas, Magister en Gestión de Base de Datos, Magister en Educación, Ingeniera en Sistemas. Universidad Técnica de Ambato. blancarcujic@uta.edu.ec
2. Aspirante a Doctor en Ciencias Informáticas, Magister en Tecnologías de la Información y Multimedia Educativa, Ingeniera en Sistemas. Universidad Técnica de Ambato. wilmalgavilanesl@uta.edu.ec
3. Magister en Docencia, Ingeniera de Sistemas. Universidad Técnica de Ambato. rk.sanchez@uta.edu.ec