ISSN 0798 1015

Vol. 38 (Nº 53) Año 2017. Pág. 8

Aplicación de la teoría de juego en la sostenibilidad de las empresas

Application of game theory in the sustainability of companies

María Elena MURRIETA Oquendo 1; María Mercedes BAÑO Hifóng 2; Marwin Leandro LAVAYEN León 3

Recibido: 27/06/2017 • Aprobado: 25/07/2017

Contenido

1. Introducción

2. Marco teórico y conceptual

3. Materiales y métodos

4. Análisis

5. Conclusiones

Referencias

1. Introducción

Las Metas propuestas por las Naciones Unidas para el Desarrollo Sostenible (Sustainable Development Goals – SDGs) abarcan una aproximación universal a la agenda de desarrollo sostenible. Explícitamente se busca que las empresas usen la creatividad y la innovación para direccionar los retos del desarrollo y reconoce la necesidad de que los gobernantes apoyen los reportes de sostenibilidad. Las meta 9 de las metas definidas por las Naciones Unidas para el 2030 mencionan:

Meta 9: Construir una infraestructura flexible, promover la industrialización inclusiva y sostenible y fomentar la innovación. “La Agenda 2030 para el Desarrollo Sostenible se adoptó en una cumbre de alto nivel en septiembre 2015, donde se presentaron un conjunto de metas de desarrollo sostenible universal, orientadas a la acción, dando lugar a una alianza mundial renovada para el desarrollo, con el respaldo de la sociedad civil, el sector privado, los parlamentarios y la comunidad científica y académica”. (United Nations, 2016).

La Teoría de Juego estudia la competencia y cooperación entre varios actores envueltos usando métodos matemáticos. El rango de aplicaciones es diversos, desde preguntas estratégicas hasta comprender la competencia económica, problemas económicos o sociales, el sistema de votos, la distribución del comportamiento de animales en situaciones competitivas, entre otras situaciones. La teoría de Juego es una disciplina matemática oficial, American Mathematical Society Classification code 91A, pero esto es desarrollado y aplicado mayormente por economistas. Artículos y libros de Economía sobre Teoría de Juego y sus aplicaciones son encontradas en Revistas de Economía Literaria de código C7x (Peters, 2015).  El Equilibrio de Nash (1950), fue la primera propuesta que probó que en cada juego, cada jugador tiene varias decisiones finitas (zero sum o non-zero sum)  es decir que pare alcanzar el equilibrio debe tener una mezcla de estrategias. Aunque Cournot (1838) desarrollo amplios estudios sobre el equilibrio de los juegos, otros autores como Shapley (1953: 1967)  mostraron la importancia del valor y la habilidad para los juegos con utilidad transferible

2. Marco teórico y conceptual

La sostenibilidad es el concepto central del ambientalismo y hace alusión a la posibilidad continua de producir y reproducir la vida en respetando el medio ambiente, desde perspectiva, la modernización del aparato productivo de un país, debe basarse en la construcción de proyectos alternativos de civilización con racionalidad ambiental        (Vargas, 2005; Brand, 1996).

El Global Reporting Initiative – GRI G4 (Empowering Sustainable Decisions), es una organización internacional independiente, que da soporte a empresas, gobiernos y a otras organizaciones, sobre el impacto que tienen las empresas en el sistema productivo, a través de factores críticos de sostenibilidad como el cambio climático, derechos humanos, corrupción y muchos otros. Describir y caracterizar las empresas en base a estos factores de sostenibilidad, es una herramienta que puede coadyuvar en beneficio de la formulación de políticas de gobernanza locales y regionales (GRI, 2014) (Galindo, Vaz, & Noronha,  2015; V.Villardon, G. Villardon, & Blazquez-Zaballos, 2006; Demey, V. Villardon, Galindo, & Zambrano, 2008).

La Innovación, está definida como invención, desarrollo e implementación de nuevas ideas, ha sido siempre importante para la continuidad de la validación de las empresas, regiones y economías (Garud, Tuertscher, & Van de Ven, 2013). Desde la formación germinal de una idea ha impactado sobre la sociedad, la innovación es una fuente de transformación del cambio (Mokyr, 1990). Así, la innovación sirve como motor orgánico para el crecimiento de las empresas (Hess & Kazanjian, 2006) (Van de Ven, Polley, Garud, & Venkataraman, 1999), como un catalizador para el desarrollo regional (Saxenian, 1996), y la base de la ventaja competitiva de las naciones (Nelson, 1993; Porter, 1990).

La innovación es actualmente un importante conductor para el crecimiento en algunos países. Las empresas en algunos países afiliados a la Organización para la Cooperación y el Desarrollo Económicos (OECD) ahora invierten tanto en activos intangibles como en Investigación y Desarrollo (I&D), software, base de datos y perfiles, como el capital físico, equipos o estructuras. El crecimiento del Multifactor Productivo (Multifactor Productivity – MFP) está estrechamente relacionado con la innovación y mejoramientos en la eficiencia. Estimaciones preliminares indican que la innovación en  Austria, Finlandia, Suecia, el Reino Unido y los Estados Unidos, invierten en activos intangibles y el crecimiento del Multifactor Productivo (MFP), juntos forman parte de las dos terceras partes y tres-cuartas partes del crecimiento de la productividad laboral entre 1995 – 2006 de estos países. En el plan estratégico de acción del OECD para alcanzar las metas propuestas por las Naciones Unidas para el 2030 respecto a la innovación, incluye aspectos como: apoyar a los países como ellos identifican donde ellos normalmente están en relación a los del SDGs, donde ellos necesitan estar y proponer caminos sostenibles basados en la evidencia; reafirmar su rol como fuente referente de experiencia, buenas prácticas y standard; fomentar la carrera de llegar al máximo como referente para mejores políticas. (Organisation for Economic Co-operation and Development, 2016)

Algunos estudios han demostrado que la sostenibilidad de las corporaciones está asociada con la administración del conocimiento (KM – Knowledge Management) y su capacidad de informar a su entorno de las prácticas que apuestan por un mejor ambiente y calidad de vida de la población de las cuales se benefician. Desarrollar una estrategia de KM es la habilidad central del concepto de sostenibilidad, como mejoramiento en la forma del bien denominado conocimiento que es administrado y reportado, esto puede liderar como la mejor que tienen las corporaciones para gobernar, facilita un continuo mejoramiento, aumentar el valor para los “stakeholders”  y proveer una sustentable ventaja competitiva (Goel, Rana, & Rastogi, 2010).

“Algunas aplicaciones de la Teoría de Juego son más exitosas que otras. Dos aplicaciones exitosas son el remate” (Klemperer, 2004; Krishna, 2002; Milgrom, 2004), y  “emparejar “(Roth, 2008). Muchos de estos recursos usados por el gobierno, que han significado implicaciones en los ingresos y para la eficiente colocación de los recursos. Los remates han llegado a ser un mecanismo para las empresas para definir el precio de sus productos, la inclusión relativa de nuevos productos como publicidad en línea. También los recursos de la teoría de juego son usados como algoritmos para emparejar el perfil profesional con los empleadores, como también estudiantes y escuelas. En el diseño de mercados y publicidad de los participantes en ese mercado es una oportunidad para la teoría de juegos (Samuelson, 2016).

Una de las aplicaciones de la teoría de juegos que ha tenido poco éxito ha sido en el campo de la negociación. Edgeworth (1881) identificó el problema de negociación como un punto básico de partida para los estudios económicos. No obstante, por décadas se ha esperado que los resultados de una negociación sean eficientes, pero el razonamiento económico no ayuda a identificar cual es típicamente los resultados eficientes que deben aparecer. Nash (1950, 1953) en sus investigaciones estudia sobre el problema de negociación. Rubinstein (1982) analiza el rol de la negociación en la teoría de juego.  Sin embargo, una preocupación del modelo de negociación de la teoría de jugos es que los resultados son muy sensitivos para la afinación de detalles del modelo. Así, el tiempo de la oferta y el tiempo de la contra-oferta, la estructura específica de la información, la longitud del horizonte, la longitud del periodo del tiempo y otros detalles (Samuelson, 2016).

3. Materiales y métodos

El método que se usará es la Teoría de Juegos de Negociación de Nash (1950), la aplicación no será bajo el esquema de una negociación sino como la toma de decisiones entre dos estrategias que podrían conducirme a los mismos objetivos, y que a su vez tienen sub-rutas que apoyan a las estrategias.  Al principio se tomará la explicación de la Teoría de Juegos de Negociación de Nash, que la realizó Peters (2015) en su libro, y luego la aplicación. Debe considerarse que se observará figuras provenientes del libro por ser las más claras para la comprensión del proceso del Juego y no consta la explicación de la obtención de los valores que se colocan en la Bimatrix.  El Juego de Negociación: es una teoría enfocada a un acuerdo entre dos jugadores individuales.

3.1 Problema de división

Dos jugadores deben estar de acuerdo en la división de una unidad perfectamente divisible, un litro de vino. Si ellos están de acuerdo entonces (α, β ) donde α,β ≥ 0 y α+β ≤1, ellos deben dividir en una unidad o no reciben nada. Los jugadores tienen preferencias por la funcionalidad del bien.

Figura 1. Solución de Negociación de Nash entre dos
jugadores que se dividen un litro de vino. (Peters, 2015)

3.2 Forma estratégica

En un juego cuando es extenso es importante distinguir entre acciones y estrategias. Una “acción” es posible cuando el jugador puede hacer un movimiento solo con un conjunto de información. En la figura 2, el Jugador 1 tiene las acciones A, B, C, a y b; el Jugador 2 en la misma figura 2 se muestra sus acciones l, r, L, R. Una Estrategia es un “plan” para jugar el juego (Peters, 2015).

Figura 2.  Acciones del Jugador 1 y Jugador 2
en la Forma Estratégica. (Peters, 2015)

Un juego extensivo se describe como un juego de árbol, como árbol tiene nodos y aristas. Cada nodo es una decisión para el Jugador, o un cambio o un final. Cada arista corresponde a una acción del Jugador o una decisión hecha por un cambio, algunas veces denominada como movimiento natural.  Una posible Estrategia para el Jugador 1 es: empezar jugando C, si el cambio de movimiento del juego resulta D entonces juega b. Otra Estrategia para el Jugador 1, es empezar jugando A, si el cambio de movimiento del juego resulta D, entonces juega b. Esta última estrategia obliga al Jugador 1 a cambiar de acción; se podría eliminar según Peters (Peters, 2015).

La estrategia para el Jugador 2 puede ser: Si el Jugador 1 juega A o B, y juega L si el Jugador 1 juega C y el cambio de movimiento resulta U. Nótese que el Jugador 2 no puede hacer su acción contingente si es que el Jugador 1 juega A o B, si el Jugador 2 no tiene la información. En el caso de que se tenga la información completa en el juego, como se muestra en la figura 3,  la estrategia del Jugador 2 debería ser que el Jugador 2 juega A y que él juega B. Una posible estrategia: Si el Jugador 1 juega A, juega r´ si el Jugador 1 juega B y juega L si el Jugador 1 juega C y si el cambio de movimiento resulta en U (Peters, 2015).

Figura 3.  Acciones con información completa del Jugador 1
y Jugador 2 en la Forma Estratégica. (Peters, 2015)

Por lo que se puede definir que la estrategia es un listado de acciones cada una de un conjunto de información del Jugador. Así, una estrategia del Jugador 1 es por lo tanto un listado de dos acciones que cada acción consta de un conjunto de información. El número posible de estrategias del Jugador 1 es el número de diferentes listados de acciones. El Jugador 1  tiene tres posibles acciones en el primer conjunto de información y dos posibles acciones en el segundo conjunto de información, este número sería igual a 3x2=6. El conjunto de estrategias del Jugador 1 sería: (Aa, Ab, Ba, Bb, Ca, Cb) (Peters, 2015). Para el Jugador 2 en el caso de que el juego tiene información incompleta de la figura 2, el Jugador 2 tiene 2x2=4 diferentes estrategias y serían: (lL, ll´,rL, rR). En el caso de que la información es completa en el juego, el Jugador 2 tiene tres conjunto de información y dos acciones, entonces sería 2x2x2=8 diferentes estrategias y se denominarían así: (ll´L, ll´R, lr´L, lr´R, rl´L, rl´R, rr´L, rr´R) (Peters, 2015).

Es importante distinguir entre la combinación estratégica y el resultado asociado. El resultado es el juego inducido del juego, es la ruta seguida en el juego del árbol. La razón más importante para considerar la estrategia de la forma extensiva del juego es la reducción efectiva a una sola oportunidad del juego. Una vez fijada la estrategia se puede calcular la ganancia siguiendo la ruta del juego del árbol.

Figura 4.  Resultados de las decisiones estratégicas tomadas por el Jugador 1
y Jugador 2 en la Forma Extensiva del Juego o Bimatrix. (Peters, 2015)

Es resultado es la bimatrix del Juego mostrado en la figura 4. Esta bimatrix se denominada estrategia de la forma extensiva del juego. La definición de Nash (Nash J. F., 1950) del equilibrio de la forma extensiva del juego es entonces: “El equilibrio de Nash de la forma extensiva del juego es la forma estratégica” (Peters, 2015).

3.3 Solución a la negociación de Nash

De acuerdo a Nash (1950), la solución a la negociación es satisfecha por cuatro condiciones: Optimo Pareto, simetría, escala de covarianza e independencia de alternativas irrelevantes.

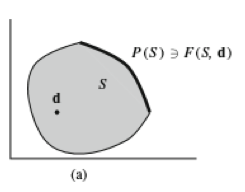
En el ejemplo para la definición, dos personas en un problema de negociación donde S es la factibilidad y d es el punto en desacuerdo. En las gráficas se observa las cuatro condiciones.

Figura 5.  El diagrama sobre el problema de negociación. (Peters, 2015)

------

Figura 6.  El diagrama de Óptimo Pareto donde S es la parte
curva en negrito. El problema de negociación F . (Peters, 2015)

-----

Figura 7.  El diagrama de Simetría, la simetría de F está señalada
en la línea delgada negra del segmento. (Peters, 2015)

-----

Figura 8.  La escala de Covarianza, se escoge d para el origen y T es el
resultado de multiplicar S por primeras coordenadas por dos.
F1 (T,d) = 2 F1 (S,d).(Peters, 2015).

------

Figura 9.  La independencia de alternativas
irrelevantes. (Peters, 2015)

3.4 Aplicación

Para que las empresas sean sostenibles en los mercados pueden hacerlo invirtiendo en Innovación o en el Knowledge Management. Si decide invertir en Innovación puede hacerlo orientada en el mercado, en el talento humano, en tecnología o en el proceso.  

Las hipótesis que se plantearan para definir la estrategia más conveniente para la sostenibilidad de las empresas y así invertir en la implementación de esa estrategia, los resultados que se tomaran serán los indicadores del GRI4  para la inversión en el Knowledge Management y los indicadores del OECD para la inversión en innovación.  

Algunos indicadores se ven reflejados a nivel macroeconómico como es en el Producto Interno Bruto de los países. Otros se encuentran reflejados indirectamente. Para usar el Árbol de Juego de Negociación de Nash para definir qué estrategia usar para la sostenibilidad, se usara números binarios: 1- reflejado directamente y 0 – reflejado indirectamente. Si es indirectamente puede representar una desventaja para requerimientos Gubernamentales que podrían ser una ventaja competitiva.

Las rutas son: ruta 1 – Innovación y ruta 2 – Knowledge Management; las subrutas: subruta 1 – recursos humanos, subruta 2 – tecnología, subruta 3 – mercado y subruta 4 – procesos. Existen varias subrutas para llegar a la sostenibilidad y muchas de esas subrutas pueden ser usadas por las rutas.

Desarrollando el árbol de decisión tenemos:

Figura 10. Diagrama de árbol donde se muestra el camino estratégico.

Se planearían las hipótesis de acuerdo a las rutas y sub-rutas y la valoración binaria (1 o 0), de acuerdo a la agencia mundial que lo refleje directamente o indirectamente.

Hipótesis 1:

La Sostenibilidad depende de la Innovación a través del Talento Humano y se muestra en el indicador del GRI4 con una valoración binaria (1,1).

Hipótesis 2:

La Sostenibilidad depende de la Innovación a través de los Procesos y no se muestra directamente en el indicador GRI4 con una valoración binaria (1,0).

Hipótesis 3:

La Sostenibilidad depende de la Innovación a través de la Tecnología y se muestra en el indicador del OECD con una valoración binaria (1,1).

Hipótesis 4:

La Sostenibilidad depende de la Innovación a través del Mercado y se muestra en el indicador del GRI4 con una valoración binaria (1,1).

Hipótesis 5:

La Sostenibilidad depende de la Innovación a través del Knowledge Management y se muestra en el indicador del GRI4 con una valoración binaria (1,0).

Definidas las estrategias a través de  rutas, sub-rutas y valoraciones, faltaría de armar la Bimatrix donde se observaría el equilibrio de Nash y así decidir la mejor ruta.

Tabla 1. Estrategia y Valoración del Juego
de Negociación de Nash. Autor (2017).

Las valoraciones más altas se escogerían: (AC, ABD), (AC, ABF) y (AC, ABG).

4. Análisis

En la Bimatrix de Nash se escoge las estrategias con valoraciones altas, lo que significaría que la ruta de la Sostenibilidad es a través del Knowledge Management apoyada por  la inversión en talento humano, o en el mercado, o en la tecnología; no se precisa que la ruta a través del proceso sea la más apropiada. No se escoge la ruta a través de la innovación.  No se usó la Solución del Juego de Negociación de Nash por el tipo de información que se usó para dar las valoraciones.

La aplicación del juego de Negociación de Nash falta definición en porcentajes de inversión que realizan las empresas, esto puede ser valorado basado en históricos de inversión realizados por las empresas. Esta sugerencia se vería reflejada en la Bimatrix y los resultados podrían cambiar. Para establecer una mejor decisión de inversión debe obtenerse mayor y mejor información. 

5. Conclusiones

Con el apoyo del Árbol de Decisión de Negociación de Nash permite ser adaptado a diferentes tipos de aplicaciones de tipo administrativa, industrial o empresarial. Sin subestimar el estudio, para un resultado idóneo en la aplicación, el limitante es la información que se requiere para un mejor armado. Por lo que con esta neuva información la valoración, incluso la ruta y sub-ruta podrían ser cambiadas y los resultados mostrarían totalmente diferente a los obtenidos. No se usó la solución del juego de Negociación sugerida por Peters (Peters, 2015) en donde Nash  muestra su teoría.

Referencias

Brand, P. ((1996).). La Sensibilidad Ambiental en la condición Posmoderna. . Revista Extensión Cultural No 36.

Cournot, A. (1838). Recherches sur les principes mathématiques de la théorie des richesses [Englishtranslation Researches intothemathematicalprinciplesofthetheoryofwealth]. . New York: Macmillan.

Demey, J. R., Vicente-Villardon, J., Galindo, M. P., & Zambrano, A. Y. (2008). Identifying molecular markers associated with classificationas of genotypes by external logistic biplot. Bioinformatics 24, 28 - 32.

Edgeworth, F. (1881). Mathematical Psychics. Kegan Paul, 20 - 30.

Franco Vargas, R. (2005). La sostenibilidad: una postura autocritica de la sociedad industrial. Investigación y Desarrollo Vol 13, 32 - 59.

Garud, R., Tuertscher, P., & Van de Ven, A. H. (2013). Perspectives on Innovation Processes. Academy of Management Vol. 7, No. 1, 775–819.

Goel, A., Rana, G., & Rastogi, R. (2010). Knowledge Management as a Process to Develop Sustainable Competitive Advantage. South Asian Journal of Management 17.3, 104 - 116.

GRI. (2014). GRI - Global Reporting Initiative. Obtenido de www.globalreporting.org

Hess, E., & Kazanjian, R. (. (2006). The search for organic growth. Cambridge: Cambridge University Press.

Klemperer, P. (2004). Auctions: Theory and Practice. Princeton University Press.

Krishna, V. (2002). Auction Theory . Academic Press.

Milgrom, P. ( 2004.). Putting Auction Theory to Work. Cambridge University Press.

Mokyr, J. (1990). The lever of riches: Technological creativity and economic progress. San Francisco, CA: Jossey-Bass.

Nash, J. F. (1950). The Bargaining Problem. Econometrica 18, 155–162.

Nash, J. F. (1951). Non-cooperative games. Annals of Mathematics 54, 286 - 295.

Nelson, R. (1993). National innovation systems: A comparative analysis. New York: Oxford University Press.

Organisation for Economic Co-operation and Development. (2016, Enero). www.oecd.org. Obtenido de www.oecd.org: http://www.oecd.org

Peters, H. (2015). GameTheory AMulti-Leveled Approach. Berlin: Springer-Verlag Berlin Heidelberg .

Porter, M. (1990). The competitive advantage of nations. New York: The Free Press.

Roth, A. E. (2008a). Deferred Acceptance Algorithms: History, Theory, Practice, and Open Questions . International Journal of Game Theory 36(3), 537 - 569.

Roth, A. E. (2008b). What Have We Learned from Market Design? Economic Journal, 118(527), 285–310.

Rubinstein, A. (1982). Perfect Equilibrium in a Bargaining Model. Econometrica 50(1), 97–109.

Samuelson, L. (2016). Game Theory in Economics and Beyond. Journal of Economic Perspectives, Volume 30, 4, 107 - 130.

Saxenian, A. (1996). Regional advantage: Culture and competition in Silicon Valley and Route 128. . Cambridge, MA: Harvard University Press.

Shapley, L. S. (1953). A value for n-person games. In: A. W. Tucker & H. W. Kuhn (Eds.), Contributions to the theory of games II). . Princeton: Princeton University Press, 307–317.

Shapley, L. S. (1967). On balanced sets and cores. ,. . Naval Research Logistics Quarterly, 14, 453– 460.

United Nations. (2016). United Nations. Obtenido de www.un.org

Van de Ven, A., Polley, D., Garud, R., & Venkataraman, S. (1999). The innovation journey. New York: Oxford University Press.

Vicente Galindo, P., Vaz, E., & Noronha de, T. (2015). How Corporatin Deal with Reporting Sustainability. Assessment Using the Multicriteria Logistic Biplot Approach. Academic Editors: Graham Winch and Carmine Bianchi. 3, 6-26.

Vicente-Villardon, J. L., Galindo-Villardon, M. P., & Blazquez-Zaballos, A. (2006). Logistic Biplots. In Multiple Correspondence Analysis and Related Methods. Statistics in Social and Behavioral Sciences Series: Boca Raton, FL, USA, 503 - 521.

1. Escuela Superior Politécnica del Litoral, ESPOL, Facultad de Ingeniería Mecánica y Ciencias de la Producción, Campus Gustavo Galindo Km 30.5 Vía Perimetral, P.O. Box 09-01-5863, Guayaquil - Ecuador

2. Universidad Católica de Santiago de Guayaquil / Universidad Santa María, Campus Guayaquil - Ecuador. E-mail: mercedes.bano@pucp.pe

3. Universidad Santa María, Campus Guayaquil - Ecuador