ISSN 0798 1015

Vol. 38 (Nº 49) Year 2017. Page 33

Analyzing Accuracy and Sensitivity in Forecasting at the Variant Level

Análisis de la precisión y sensibilidad en la previsión a nivel de variante

Albert Lutfullovich BIKMULLIN 1; Boris Petrovich PAVLOV 2; Khanifovich Khusainov ZUFAR 3

Received: 30/09/2017 • Approved: 05/10/2017

Content

1. Introduction

2. Methods

3. Discussion

4. Conclusions

References

1. Introduction

The current level of the national economy development significantly increases the requirements for planning and managing its various branches. As the interaction and dependence of all economy layers are intensifying, one has to consider the interacting variety of objective and subjective, internal and external factors; to foresee the future consequences of measures taken with the forecasting methods when managing production and economic processes (Bikmullin, 2017). The research, conducted for the purpose of improving the existing and developing new methods and procedures of scientific forecasting, is obviously relevant, as these methods and procedures will allow orienting the specific sector development (Bikmullin, 2012). The existing approach towards scientific forecasting, analyzed by the leading scientists from different countries, shows that forecasting is considered as a methodology, namely – a set of operations and provisions that allow successfully applying objective mathematical methods and intuitive techniques to determine the scenario trends and variants of in the broad sense of the word (Kashtanov, 2014), Vatutin V.P. Ivchenko G.I. Medvedev Yu.I. Chistyakov V.P. (2015), Sadovnikova N.A., Shamaylova R.A. (2016), Jeston J. Nelis J. (2014), Oakland J.S. (2011), Lars Lonnstedt, (1975), Thad W. Green, W.B. Newsome, and S.R. Jones, (1977)]. At the same time, system approach should be the most important feature of the forecasting methodology. There are research papers, written by the leading scientists of different countries, devoted to the problem of scientific and technical forecasting (Jantsch, 1970; Loomba, 1978; Hill et al, 1970; Chambers et al, 1971; Albertson and Cutler, 1976; Centron and Ralph, 1971). However, despite some progress in solving these problems, there are methodological problems that remain insufficiently worked out and adapted for specific production branches. In particular, Davenport W.B., Johnson R.A. and Middleton D. draw their attention to the process of calculating the variance of correlation functions (Davenport et al, 1962). However, this is not enough if you wish to analyze the forecast accuracy and reliability completely. In our opinion, forecast reliability and sensitivity of forecast variants to changing external environment, as well as the system quality assessment, should also be clearly distinguished. The famous English scientist Grenander (1961) has noted that a variable characterizing accuracy can also be defined as the reliability of structural function prediction. Foreign and domestic studies emphasize that accuracy is an important forecast parameter. Thus, it is important to understand how to assess it. Oakland (2011) highlights that statistical methods are important for implementing the approach; they are widely used among many researchers. Kutin V.N. (1964), Livshits I.A. and Pugachev V.I. (1963) note that the bigger is the number of observations used in forecasting, the more accurate is the forecast. Our method of assessing the forecast accuracy allows us not only to significantly refine the estimates, but also to assess the sensitivity of forecast variants. It should be stressed that such definition of forecast reliability is applied only to quantitative regularities. In terms of qualitative, weakly structured aspects of forecasting, there are methods for assessing the probability by means of expert surveys. As in any research with experts, a proper program – ways the questions are put and the basic data are submitted, etc – is very important for measuring sensitivity. The purpose of the article is to develop a methodology for assessing the scenario variants based on the processes of comparing alternative solutions and selecting the optimal ones through the expert assessments. Such a study was not presented earlier.

2. Methods

Let’s move to analyzing the reliability of dependencies, derived on the basis of retrospective quantitative data. In this case, forecast multivariate comes down to the upper, the lower and most probable scenario trends. The curve run is largely determined by the retrospective sample representativeness. In analyzing reliability, one has to consider not only the random future effects that may affect the scenario, but also the random effects of the past, since the initial information about the system is accidental in nature. In other words, we do not know what parameter values are true and which are random. This paper describes a correct method for measuring the forecast reliability.

First and foremost, we have to find the lower and upper scenario boundaries. We have used a method of statistical prediction, based on simple mathematical models describing the regularities Y=f(t), where “t” is time.

We have used these methods because specific values ​​of each indicator are dependent on many factors, most of which cannot be considered and controlled. Therefore, each studied indicator is a random variable with a normal distribution. Naturally, there are factors determining the general scenario pattern and factors determining its actual level variations.

In predicting the change in the indicator over time, the following mathematical model is often proposed for use:

Where: m(t) – ordinary, non-random function, which is assumed to be known. The function X(t) characterizes the effect of unconsidered factors, namely – determines the noise level and the degree of its impact. This problem involves the prediction of a random process structure based on data available from past observations on noise, as well as the forecast accuracy and reliability assessments.

Let’s make some natural assumptions about the process X(t).

The process X(t) is a stationary and steady process without any trend. The basic configuration m(t) is said to include all the clearly expressed trends. The mean value Ex(t) of the noise component is zero.

The process X(t) is considered to be a Gaussian process. In other words, all finite-dimensional distributions of the process are normal. Since the noise impact degree is covered by the constant a, the process X(t) is naturally considered to be normalized to:

Dx (t) = 1

The process X(t) is S-related. In other words, there will be no relation between х (t1) and х (t2) if (t1-t2)> S. This is an ordinary prerequisite for the generalized Markov noise component, entailing the ergodic nature of the process X(t). The latter means that almost any process trajectory contains information.

We assume that the process is completely determined by the structural (correlation) function r (t1, t2)=Eх (t1)х (t2), where r (t1, t2 )=r (t2-t1)=r-(t1-t2),  as the process is stationary, and r (t2-t1)=0 for (t1-t2) >S, as the process is S-related.

The point estimate r*(t) available from the observations is usually considered as the prediction of a true structure function r (t). This is followed by an inadvertent error:

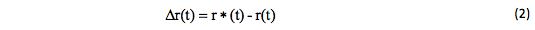
Therefore, the question arises about the forecast accuracy and reliability. In this case, we can judge from the probability that the absolute value of the error Δ r (t) will be less than a certain value:

In this equation, r* value characterizes the forecast accuracy; probability P, determines the reliability of the structural noise function prediction.

For simplicity, let’s consider the sequence case, where the time varies discretely and possesses the values 0,1,2…

Accprding to the ergodic theorem for the stationary processes, the equation with probability 1 will be as follows:

Let’s assume that we have (n +1) process values: х(о), х(1),... х(n).

Let’s consider

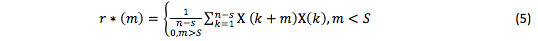
as the structural function prediction.

Obviously, r*(m) is a value of a random variable, which is known to be asymptotically the most effective and to have no regular errors [Mikhaylov O.V., Oblakova Т.V. (2014), Galazhinskaya O.N., Moiseeva S.P. (2015)]. Since Kutin V.N. (1964), Livshits I.A. and Pugachev V.I. (1963) calculate the variance of predicted and true structure functions:

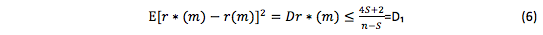
This estimate is higher than it suppose to be. The following value is more accurate:

All these estimates arise quite simply based on:

According to the estimates D1 and D2, the variance will tend to 0 if n → ∞. In other words, the bigger was the number of observations used in forecasting, the more accurate will be the forecast.

If we fix some values of m (<S), then rm(k)=X(k+m)X(m)-r(m) will be a stationary  process.

Moreover, rm(k) and rm(L) are independent for (k+m-L)>S because of the noise x(k). Thus, the process rm(k) satisfies the condition of uniform strong mixing and falls within the central limit theorem (CLT) for stationary processes

Thus, as n → ∞ and m is fixed:

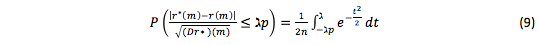
One can assess the forecast accuracy and reliability by this formula with the normal distribution tables [Yanko Ya 1981].

Information available from observations, except the prior D1 and D2 estimates, allows us to significantly refine the estimates. Therefore, one has to carry out the largest number of observations beforehand in order to calculate the forecast variance more accurately.

When it comes to the qualitative features of an object (especially structural changes), one has to assess the alternatives not only by criteria characterizing the efficiency, but also by its interaction with the changing environment. In other words, one has to assess the sensitivity of forecast variants in order to make the easy-to-use prediction.

In this paper, object quality is its ability to perform functions at particular level of efficiency under given conditions. Obviously, object quality involves its positive and negative properties, assessed by a particular criterion.

Variant quality assessment is a functional of estimates for the forecast variant properties and the external environment. Its structure is determined by the nature of system relations and by the importance of its properties. Naturally, any formula that unites the various system properties (by complex criteria) cannot adequately reflect its quality. Therefore, quality assessment cannot be the only method; it is useful for comparing different variants among each other, since the same procedures are used to assess them. Consequently, quality assessment is relative. Currently, there is a number of models used to compare the alternatives:

- multiplicative-representative model:

Where: n is the number of criteria characterizing the given system when solving a particular problem;
wi, wj – criteria weights;
ai, aj – values ​​of variant properties measured by criteria;
ai, wi – for favorable factors;
aj, wj – for unfavorable factors,

Favorable factors are those, which increase in number raises the overall P estimate; unfavorable factors are those that bring it down as they increase in number.

The optimal variant is that at which the P estimate is the maximum possible.

One has to be particularly focused when dealing with such an estimate. Estimates аi and аj must be greater than 1 to preserve the order after raising them to the wi and wj power. There will be difficulties if some estimates are equal to 0. In these cases, Р(1) turns either into 0 or into ∞.

In particular cases, such estimate is important. However, in most cases, it is good for nothing

Disadvantages of the Р(1) estimate can be overcome in the following assessment:

In this case, zero criteria estimates do not affect the value of the overall estimate. However, this form is also imperfect, since the estimate value may be negative. The optimal variant involves the process of selecting by a minimum negative value. However, this is aesthetically imperfect and makes the expert’s work more difficult.

The following additive model has no previous drawbacks:

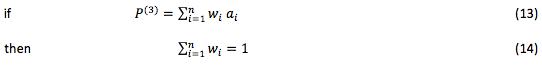
Where: аj is inverted into ai. In other words, this estimate value was normalized to a minimum value instead of a maximum value. For example, reliability as a failure rate (unfavorable factor) is changed into the mean time between failures (favorable parameter).

In this case, the highest estimate corresponds to the best variant.

The multiplicative-weighted model has no shortcomings of the first two models:

Where: aj is inverted into ai. In other words, this estimate value was normalized to a minimum value instead of a maximum value, but this form is less informative then the previous one.

The optimal variant also corresponds to the maximum Р value.

Sensitivity criterion is a system criterion of assessment, as is easily understood from its definition.

In system analysis, sensitivity is usually considered as the degree of system quality stability in relation to certain changes in affecting factors; it may happen that the variant, optimal in one case, will prove to be useless in other cases.

The process of measuring sensitivity partakes somewhat of measuring the derivative of a function of many variables. All the active factors are fixed; one of them varies in strictly defined limits. Thus, quality dependence on the factor variations is measured. Naturally, such method is absolutely unacceptable in measuring the sensitivity of forecast variants in industry, since an experiment with such an object is impossible. Moreover, data on the factors’ affect on the system in the past are unreliable and incomplete.

In this case, experiment with the model of an object is the only possible method. We assumed that the more complete is the model’s object description, the more reliable will be the measured sensitivity values. However, further analysis has shown that the process of measuring sensitivity with a model at the modern level of knowledge is a very difficult challenge, as the system depends on a variety of factors. It is not always possible to consider them even when the system relationships are introduced in the model. It is not often possible to build a quantitative description either. In addition, expert polling is a difficult process to conduct.

Further, system quality is assessed on the basis of several estimates measured for various system properties according to pre-selected criteria. Consequently, based on one factor’s variation from the minimum to the maximum possible value, we will obtain two quality estimates, respectively. If the model introduces N factors, then we will have 2N estimates. Thus, result analysis is unlikely to be possible.

In the first approximation, variation procedure is as follows: weight coefficients have three values: 0.9 nominal, nominal, 1.1 nominal. Properties are divided into two groups: positive and negative. In setting values that are below, above and equal to the nominal (independently of each group), we obtain 9 estimates.

Forecast variants are selected as follows: sensitivity analysis for each variant provides a nominal, maximum (not necessarily, if all weights are higher than the nominal) and minimum estimates. Let’s consider two variants – A and B.

If the minimum estimate for the alternative A available from the sensitivity analysis is above the maximum one for the alternative B, one can state that alternative A is better than B. It should be noted that A can dominate without being dominant by criteria, namely – without higher estimates among the variants.

If the nominal estimate for A is above the maximum one for B, we conclude that the variant A is the best one. If the maximum estimate for B is above the minimum for A, we conclude that the variant B is the best one (although the difference is small). If the nominal estimate for A is below the maximum one for B and above the nominal one for B, variant A turns to be a questionably better. If the minimum estimate for A is below the nominal one for B, the choice between A and B will be open to question.

In the last case, one has to whether check the significance of original criteria, any changes in the system, new information, and the ability to achieve characteristics or change flexibility, or re-assess the correlation of any other gaps revealed in the first set of estimates. The new added variants also have to be re-assessed. 

3. Discussion

The conducted researches make it possible to conclude that the success of forecasting is determined by the availability of more complete information about the object, by combined theoretical and empirical knowledge and by the information about the phenomena that affect the scenario. It should be noted that in measuring the forecast reliability, forecasting method is used only if there is a statistical reliable dependence between variables. In terms of qualitative, weakly structured aspects of forecasting, there are methods for assessing the probability by means of expert surveys. The future status of an object should be predicted in several stages with a method of successive approximations, based on constantly-refining models and results. Forecasts can be used if there are several assessed alternatives and agreed variants with real possibilities. Based on retrospective data analysis, we have developed a method for forecasting the structural process with the CLT (Ibragimov and Linnik, 1965) and the normal distribution table (Yanko, 1981) in order to assess the forecast reliability and accuracy. This assessment is more accurate than the variance calculated with correction factors. Quality assessment is a functional of estimates for the forecast variant properties and the external environment. It is measured with multiplicative-representative, representative-weighted and additive models, depending on the impact degree of favorable/unfavorable factors and weight coefficients of criteria, as well as on the expert assessment. As sensitivity criterion is a system criterion of assessment (namely, the degree of system quality stability in relation to certain changes in external factors), sensitivity is measured by calculating the derivative of a function of many variables. All the active factors are fixed; one of them varies in strictly defined limits. Thus, quality dependence on the factor variations is measured. At the same time, system quality assessment is based on several estimates according to the pre-selected criteria. The following considerations can be used as a compromise between forecast reliability and unjustified expenditures on the assessment. Since the effective factor variation affects the system quality by changing the significance of its properties, there are properties contributing to performance of functions under new conditions, and properties that do the opposite thing. The model’s factor will change the strength of relationships between variables, and ultimately, the weight coefficients of criteria. In other words, the weight coefficient determines the significance of variant property assessed by the criterion. Therefore, in analyzing the model for sensitivity, one can replace the numerous expert surveys with a variety of weight coefficients of criteria and analyze how the estimate has changed. At the same time, we have developed a certain procedure that allows selecting the most optimal forecast variants. We should also note that the analysis of research papers, devoted to the issue of measuring accuracy and sensitivity in forecasting, has shown that the issue is debatable and little studied.

4. Conclusions

The analysis shows that forecasting method depends significantly on the purpose of forecast and the nature of the studied object. Thus, acceptable forecast accuracy requires a combination of objective and intuitive methods, and the forecast itself must be built with a method of successive approximations, namely – with an iterative method. This article can be helpful for specialists engaged in production and economic processes management, as well as for decision-makers. Based on this research, it is possible to allocate a number of scientific problems and prospective directions that require certain provisions, presented in the article, to be considered, deepened and expanded in the future.

References

Albertson, L.; Cutler, T. “Delphi”. Futures. 8(5), pp. 397-404.

Bikmullin, A.L. (2017). “Methodological fundamentals of selecting forecasting methods”. "COGNITIO RERUM" online journal. 3.

Bikmullin, A.L. (2012). “Modern methods of forecasting socio-economic processes”. Materials of the All-Russian Scientific Conference "Humanitarian and Natural Sciences: Problem of Synthesis", Moscow.

Centron, N. J.; Ralph, C. A. (1971). “Industrial Applications of Technological Forecasting”. New York: Wiley.
Chambers, J. C.; Mullick, S. K.; Smith, D. (1971). “How to Choose the Right Forecasting Technique”. Harvard Business Review,  pp. 45-74.

Davenport. W.B.; Johnson. R.A.; Middleton D. (1962). “Statistical Errors in Measurements on Random Time Functions. Determining the Parameters of Random Processes”.  Kiev.

Galazhinskaya, O.N.; Moiseeva S.P. (2015). “Theory of random processes”. Tomsk State University.

Green, T. B.; Newsome, W.B.; Jones, S. R. (1977). “A Survey of the Applications of Quantitative Techniques to Production/Operations Management in Large Corporations”. Academy of Management Journal.  20, pp.670.

Grenander, U. 1961). “Stochastic processes and statistical inference”. Foreign Literature Publishing House, Moscow: Gosinoizdat.

Hill, J. W.; Bass, A. R.; Rosen, H. (1970). “The Prediction of Complex Organizational Behavior Ibragimov, I.A.; Linnik, Yu.V. (1965). “Independent and stationary-related variables”. Moscow: Nauka Publishing House.

Jantsch, E. (1980). “Forecasting of scientific and technical progress”. Progress Publishing House.

Jeston, J.; Nelis, J. (2014). “Business Process Management Practical guidelines to successful implementations”. London and New York: Routledge

Kashtanov, Yu.N. (2014). “Statistical modeling of queuing systems”. St. Petersburg State University.

Kutin, V.N. (1964). “Calculating the correlation function of a stationary random process based on the experimental data”. «Avtomatika i telemekhanika» journal [Automation and telemechanics]. 5.

Livshits, I.A.; Pugachev, V.I. (1963). “Probability Analysis of Automatic Control Systems”. Moscow: Sovetskoye Radio Publishing House.

Loomba, N. P. (1978). “Management: A Quantitative Perspective”. New York: Macmillan, p. 394.

Lonnstedt, L. (1975).  “Factors Related to the Implementation of Operations Research Solutions”. Interfaces. 5(2, I).

Mikhaylov, O.V.; Oblakova Т.V. (2014). “Random processes. Stochastic analysis”. Bauman Moscow State Technical University, Moscow.

Oakland, J.S. (2011). “Statistical Process Control”. London and New York: Routledge

Sadovnikova, N.A.; Shmoilova R.A. (2016). “Time series analysis and forecasting”. Moscow.

Vatutin, V.P.; Ivchenko, G.I.; Medvedev, Yu.I.; Chistyakov, V.P. (2015). “Theory of Probability and Mathematical Statistics in Problems”. Moscow.

Yanko, Ya. (1965). “Mathematico-Statistical Tables” [in Russian]. Gostondart, Moskow

A Comparison of Decision Theory with More Traditional Techniques”. Organizational Behavior and Human Performance. 5, pp. 449-462.

Albertson, L.; Cutler, T. “Delphi”. Futures. 8(5), pp. 397-404.

Centron, N. J.; Ralph, C. A. (1971). “Industrial Applications of Technological Forecasting”. New York: Wiley.

1. Doctor of Economic Sciences, professor of Economics and management at the enterprise department "Kazan National Research Technical University named after A. N. Tupolev – KAI, bikmullina@yahoo.com

2. Сandidate of technical Sciences, professor Of Economics and management at the enterprise, Kazan National Research Technical University named after A. N. Tupolev – KAI, priem.pavlov@mail.ru

3. Сandidate of Economic Sciences, docent, Of Economics and management at the enterprise, Kazan National Research Technical University named after A. N. Tupolev – KAI, zuf_box@mail.ru