

Vol. 38 (Nº 48) Year 2017. Page 7
Nadezhda Gennadievna CHERKUNOVA 1
Received: 12/06/2017 • Approved: 30/06/2017
2. Application of the Lagrange method to optimize production output
3. Finding the parameters of the model
5. Discussion of the results and their application
ABSTRACT: We study the optimization of production output as a process of finding the conditional maximum of the Cobb-Douglas production function in the presence of the budget constraint. This function is often used in the analysis of economic development. The use of the Lagrange method allows obtaining a stationary point of the Lagrange function. The examination of this point reveals the presence of a conditional maximum at it. The obtained coordinates of the point of conditional maximum of the output volume mean that, under the optimal functioning of the firm, i.e., such functioning, for which the greatest production output is achieved with a fixed budget, the budget should be distributed between fixed assets and labor resources in proportion to the corresponding elasticities of the production output. These coordinates allow finding the values of the largest production output and the marginal maximum output with respect to the budget. |
RESUMEN: Estudiamos la optimización de la producción como un proceso para encontrar el máximo condicional de la función de producción de Cobb-Douglas en presencia de la restricción presupuestaria. Esta función se utiliza a menudo en el análisis del desarrollo económico. El uso del método de Lagrange permite obtener un punto estacionario de la función de Lagrange. El examen de este punto revela la presencia de un máximo condicional en él. Las coordenadas obtenidas del punto de máxima condicional del volumen de salida significan que, bajo el óptimo funcionamiento de la empresa, es decir, tal funcionamiento, para lo cual la mayor producción productiva se consigue con un presupuesto fijo, el presupuesto debe ser distribuido entre los activos fijos y los recursos laborales en proporción a las elasticidades correspondientes de la producción. Estas coordenadas permiten encontrar los valores de la producción más grande y la salida máxima marginal con respecto al presupuesto. |
The transition to market economy requires that enterprises increase the production efficiency and the competitiveness of products and services through introduction of the results of scientific and technological progress, effective forms of economic and production management, overcoming mismanagement, promotion of entrepreneurship, initiative, etc.
An important role in solving this problem belongs to the economic analysis of the activity of economic entities. With its help, the strategy and tactics of enterprise development are worked out, plans and management decisions are justified, control over their implementation is realized, the reserves for increasing production efficiency are identified, and the performance results of the enterprise, its departments and employees are evaluated (Fomin 2009).
The technical and organizational level of production determines the volumes of production and the sales of products, which, in turn, serve as the basis for the formation of the main type of income, the sales proceeds. The growth in the volume of production and the increase in its quality directly affect the value of production costs, profit and profitability of the enterprise. The activities of economic entities should be aimed at producing the maximum quantity of high-quality products at minimal cost. Therefore, the analysis of the work of enterprises begins with the study of output indicators. The analysis of the production and sale of products allows assessing the competitive position of the enterprise and its ability to respond flexibly to changing market conditions.
Among social sciences, economics uses mathematics to the greatest extent. To work successfully, a modern economist must not only have good basic knowledge, but also be able to use mathematical methods to solve practical problems (Cherkunova 2011). The implementation of radical reforms in the transition to a market economy requires carrying out mathematical calculations of the future results of economic activity. The modern economy uses almost the entire apparatus of applied mathematics (Krass,. and Chuprynov 2008; Krass, 2003). Mathematical calculations are an effective means of improving management of economic activity (Cherkunova, and Novoselova, 2011); without them it is impossible to achieve good economic results. The discovered regularities related to economy are not only of theoretical value; they are widely used in practice: in planning, management and forecasting (Kremer 2002).
The present work is devoted to studying the production output optimization. This topic is of great current interest, since the growth rates of the volume of production and sales of products directly affect the value of costs, profit and profitability of the company, serve as the basis for the formation of the main type of its income, the sales revenue, and allow assessing its competitive position.
The purpose of this work is to investigate the output function in terms of the existence of a conditional maximum with the help of a system of corresponding differential equations and to find, with the help of this system, the maximum volume of the company’s output under a budgetary constraint, and the values of the largest and the marginal maximum production output with respect to the budget.
The majority of the most important concepts of economics are examples of standard concepts of mathematics. Let us consider the optimization of production output as a process of finding its maximum, i.e., choosing the best option from the set of possible ones (Braun, 1983).
As an example, we choose the Cobb-Douglas model (Kremer and Putko 2003), which is often used in the analysis of economic development. The production function in this model is a function that shows the production output Y for the capital input K and labor input L. For the case of two variables, it has the form



Figure 1. Isoquants of the Cobb-Douglas production function.
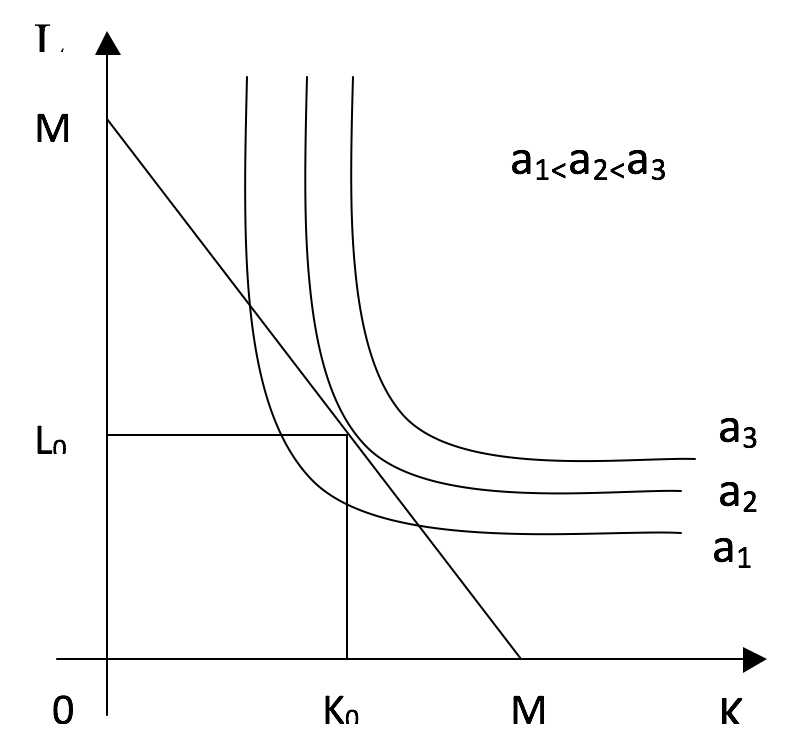

The obtained equation (3) means that, under the optimal functioning of the firm (i.e., such functioning that achieves the highest production output under a fixed budget), one should distribute the budget M between the fixed assets K and the labor resources L in proportion to the elasticities of output with respect to K and L. If we denote by Y0 the value of the largest production output

Consequently, the Lagrange multiplier is equal to the marginal maximum production output with respect to budget, i.e., if the budget is increased by 1, then the largest output will increase by λ0 units.

In the work, the function of production output was investigated, which directly affects the value of costs, profit, profitability and competitive position of the firm, whose activities should be aimed at producing the maximum quantity of high-quality products at minimal costs.
As this function, the production function Y of the Cobb-Douglas model was considered, which is often used in the analysis of the economic development. The function Y of this model expresses the dependence of the volume of output on the input of capital K and labor resources L.
To find the conditional maximum of the function Y, a stationary point (K0,L0,λ0) was found by the Lagrange method as a solution of the formed system of equations, where λ is the Lagrange multiplier. The examination of this point showed the presence at it of a conditional maximum of the output volume Y under the budget constraint K + L = M, where M is the budget of the firm.
The obtained coordinates (K0,L0) of the point of the conditional maximum mean that, under the optimal functioning of the firm (i.e., such functioning, which achieves the largest output under a fixed budget), the budget M should be distributed between the fixed assets K and the labor resources L in proportion to the elasticities of output with respect to K and L.
These coordinates allowed finding the values of the largest production output and the marginal maximum output with respect to the budget.
The author expresses deep gratitude to the Director of the Sayano-Shushensky Branch of Siberian Federal University E.Yu. Zateeva for her support in writing this article.
Braun, M. (Ed.). (1983). Differential Equation Models. New York: Springer. (p. 380).
Cherkunova, N.G. (2011). Problema prikladnoi napravlennosti matematicheskoi podgotovki ekonomistov [The Problem of Applied Orientation of Mathematical Training of Economists]. In Materialy Mezhdunarodnoi nauchno-prakticheskoi konferentsii "Krizis ekonomicheskoi sistemy kak faktor nestabilnosti sovremennogo obshchestva" [Proceedings of the International Scientific and Practical Conference "The Crisis of the Economic System as a Factor of Instability of Modern Society"] (pp. 177-178). Saratov: Izdatelskii tsentr "Nauka".
Cherkunova, N.G., and Novoselova, I.A. (2011). Differentsialnye modeli, opredelyayushchie effektivnost reklamy, spros i predlozhenie [Differential Models that Determine the Effectiveness of Advertising, Supply and Demand]. In Materialy Mezhdunarodnoi nauchno-prakticheskoi konferentsii "Analiz sovremennykh ekonomicheskikh protsessov i informatsionnye tekhnologii" [Proceedings of the International Scientific and Practical Conference "Analysis of Modern Economic Processes and Information Technologies"] (pp. 101-103). Dnepropetrovsk.
Dougherty, C. (1992). Introduction to Econometrics. New York, Oxford: Oxford University Press. (p. 402).
Fomin, G.P. (2009). Matematicheskie metody i modeli v kommercheskoi deyatelnosti [Mathematical Methods and Models in Commercial Activity]. Moscow: Finansy i statistika. (p. 640).
Krass, M.S. (2003). Matematika [Mathematics]. Moscow: Delo. (p. 704).
Krass, M.S. and Chuprynov, B.P. (2008). Matematika i ee prilozheniya v ekonomicheskom obrazovanii [Mathematics and Its Applications in Economics Education]. Moscow: Delo. (p. 720).
Kremer, N.Sh. (2002). Teoriya veroyatnostei i matematicheskaya statistika [Theory of Probability and Mathematical Statistics]. Moscow: UNITI. (p. 543).
Kremer, N.Sh., and Putko, B.A. (2003). Ekonometrika [Econometrics]. Moscow: UNITI. (p. 311).
1. Sayano-Shushensky Branch of Siberian Federal University, P.O. Box 83, house 46, Work Settl. Cheryomushki, Sayanogorsk, Republic of Khakassia, 655619 Russia. E-mail: cherkunova.52@mail.ru