ISSN 0798 1015

Vol. 38 (Nº 47) Ano 2017. Pág. 8

Dinâmicas de curto e de longo prazo na indústria da região Sul do Brasil

Short and long-term dynamics in the industry in the Southern Region of Brazil

Elano Ferreira ARRUDA 1; Andressa Paiva de ALENCAR 2; Pablo Urano de Carvalho CASTELAR 3

Recebido: 25/05/2017 • Aprovado: 25/06/2017

Conteúdo

1. Introdução

2. Revisão de Literatura

3. Aspectos Metodológicos

4. Resultados

5. Conclusão

Referências bibliográficas

1. Introdução

As discussões sobre políticas de desenvolvimento em um contexto regional têm se pautado principalmente na busca pela correção dos chamados desequilíbrios regionais, pois autores como Myrdal (1963) e Williamson (1965) advertem que o crescimento regional pode ser convergente ou divergente; ou seja, haveriam efeitos adversativos de retardamento, que se traduziriam numa redução da atividade econômica das unidades econômicas vizinhas, e de espraiamento, que promoveriam o crescimento de todas as economias vizinhas.  A convergência ou divergência regional dependeria de qual efeito prevaleceria em longo prazo.

Nessas condições, mudanças econômicas ocasionadas por choques tecnológicos, alterações nos preços relativos, oscilações climáticas ou alterações nas próprias políticas econômicas podem ocorrer em uma unidade econômica e afetar positiva ou negativamente às unidades vizinhas. O entendimento de como se dá a transmissão desses choques para as demais regiões vizinhas se mostra fundamental para o desenvolvimento regional, além de apontar para o caminho da correção de possíveis desequilíbrios inter e intrarregionais existentes.

Diante do exposto, percebe-se a importância de se estudar as dinâmicas inter e intrarregionais de uma economia com dimensões continentais como Brasil, uma vez que essa abordagem permite a verificação do quanto a atividade econômica de uma região ou estado pode afetar as demais regiões ou os demais estados de sua própria região. Nessa linha, Tatiwa e Arruda (2011) analisam a dinâmica inter-regional da indústria brasileira, numa análise de curto prazo, a partir de funções de impulso resposta de um Vetor Autorregressivo (VAR) restrito. Os autores mostram que as regiões Sul e Sudeste são as que mais promovem efeitos de espraiamento no país, enquanto que o Nordeste produz maiores efeitos de retardamento sobre as demais regiões do Brasil.

Em seguida, de modo a aprofundar o exercício supracitado, Arruda e Tatiwa (2014) promovem outro estudo empírico dessas interações, agora em um contexto intrarregional, ainda através das funções impulso resposta extraídas de modelos VAR restritos. Os autores encontram uma predominância em curto prazo dos efeitos de rivalidade ou de retardamento na região Nordeste, entre Pernambuco e Ceará, e na Região Sudeste, entre Rio de Janeiro e Minas Gerais. Todavia, seus resultados apontam para a região Sul como sendo a mais integrada, em termos de repercussões da atividade industrial. Vale destacar que os autores não incluem o Estado de Santa Catarina no modelo.  

Apesar dos importantes avanços nessa abordagem, percebe-se certa limitação nessas evidências, uma vez que esses resultados se concentram apenas em analisar a repercussão de choques na indústria em curto prazo. Diante disso, Arruda e Damasceno (2015) e Lima (2015) promovem exercícios econométricos mais amplos, através da aplicação de vetores de correção de erros (VEC), respectivamente, para as regiões Nordeste e Sudeste do Brasil, onde se pode analisar as elasticidades de longo prazo para verificar se as evidências anteriores se confirmam nesse contexto. Arruda e Damasceno (2015) observam que, em longo prazo, o Estado da Bahia parece produzir os maiores efeitos de espraiamento para a região Nordeste, enquanto que Ceará e Pernambuco parecem rivalizar entre si.

Os resultados de longo prazo observados por Lima (2015) indicam que os Estados de São Paulo e do Rio de Janeiro apresentam maiores efeitos de espraiamento sobre os estados de Minas Gerais e Espírito Santo e que estes também apresentam efeitos positivos sobre crescimento industrial daqueles.  Todavia, o autor observa indícios de que existem maiores efeitos de retardamento, ou de rivalidade, entre as indústrias de São Paulo e Rio de Janeiro e de Minas Gerais e Espírito Santo, contrariando, em parte, a evidência de curto prazo mencionada anteriormente.

Portanto, o presente estudo pretende contribuir nessa linha ao analisar as dinâmicas de curto e de longo prazo da atividade industrial da região Sul do Brasil com vistas a identificar se, de fato, esta se mostra a região mais integrada do país em termos de repercussões intrarregionais numa perspectiva de longo prazo. Especificamente, pretende-se quantificar a amplitude das elasticidades de longo prazo entre as dinâmicas industriais de seus estados, exercício ainda não realizado para essa região, além de corroborar com evidências anteriores sobre suas relações de curto prazo, adicionando a elas evidências extraídas da decomposição de variância do erro de previsão.

Para tal, são utilizados dados do índice de produção industrial, disponibilizados pelo Instituto Brasileiro de Geografia e Estatística (IBGE) em nível estadual para Rio Grande do Sul, Paraná e Santa Catarina, entre janeiro de 1995 e fevereiro de 2014, e vetores de correção de erros (VEC). Além disso, são utilizadas informações da Secretaria de Comércio Exterior do Ministério de Desenvolvimento Industria e Comércio (SECEX/MDIC), para traçar um perfil descritivo das atividades industriais desses estados e identificar as suas inter-relações.  

Além dessa introdução, o presente estudo possui mais quatro seções. A próxima seção se reserva a expor aspectos teóricos e as principais evidências empíricas no âmbito do desenvolvimento regional e algumas aplicações. Na sequência, apresentam-se os aspectos metodológicos, quais sejam, a descrição e análise do banco de dados e da estratégia econométrica. A seção quatro expõe e discute os resultados e, por fim, são traçadas algumas conclusões finais sobre o trabalho.

2.1. Aspectos Teóricos

A discussão acerca das consequências do desenvolvimento econômico em uma região concentrada é assunto de amplo debate, mas que ainda está longe de um consenso em teoria econômica. Em relação ao estudo sobre a localização e concentração da atividade econômica no espaço, Marshall (1890) foi o pioneiro na pesquisa e observou, baseado nas zonas industriais da Inglaterra no final do século XIX, a presença de externalidades que causavam vantagens competitivas que não poderiam ser obtidas caso cada produtor atuasse individualmente. O autor declarou que, dentre as principais causas do que ficou conhecido como externalidades Marshallianas, pode-se citar a existência de condições naturais, como disponibilidade de matéria-prima, fontes de energia, custos de transporte reduzidos e a existência prévia de demanda na região. Todos esses fatores propiciariam retornos crescentes de escala para os participantes do setor.

Posteriormente sugiram teorias bastante antagônicas em relação ao crescimento econômico regional. A primeira linha de pensamento, defendida por autores como Myrdal (1968) e Hirschman (1975), apoiam a teoria da visão divergente do crescimento econômico regional. Por outro lado, Williamson (1977) apresenta uma teoria que indica crescimento convergente.

Myrdal (1968) e Hirschman (1975) justificam sua teoria através dos fundamentos denominados “efeitos de retardamento” (backwash effects) e “efeitos de espraiamento” (spread effects). O efeito de retardamento ocorre devido ao incentivo na região mais industrializada causar nas regiões rurais um processo de migração da mão de obra mais qualificada, como a população mais jovem e de maior nível de educação; haveria também um maior nível de realocação de capital causado pelas novas oportunidades na região mais incentivada; o avanço traria também uma melhor infraestrutura para a região mais desenvolvida; todos esses fatores acarretariam numa vantagem comparativa que acabaria por prejudicar, ainda mais, a região menos desenvolvida.

Na direção oposta, os efeitos de espraiamento referem-se às vantagens criadas pelo desenvolvimento industrial às demais regiões, como por exemplo, aumento na demanda de insumos industriais que poderiam ser supridos pelas localidades desfavorecidas ou avanços tecnológicos que beneficiaria ambas as localidades. Como os efeitos de retardamento tendem a ser maiores que o de espraiamento, os autores defendem que o crescimento regional tende a ser desigual.

Na linha de raciocínio oposta à supracitada, autores como Williamson (1977) advogam uma visão convergente, na qual o crescimento econômico reduz a desigualdade. Tem seus argumentos baseados no fato de que, no longo prazo, as forças de mercado eliminam as desigualdades regionais. Segundo o autor, os níveis de desigualdades tendem a ser crescentes no curto prazo, no decorrer do tempo essa desigualdade atinge o máximo, porém, após esse período, há uma reversão e as desigualdades diminuem. Portanto, no curto prazo prevalece a hipótese de divergência, mas no longo prazo predomina-se a teoria de convergência de renda entre regiões.

Posteriormente surgiram modelos de crescimento regional baseado na demanda por exportações. Kaldor (1970) utilizou argumentos baseados na demanda agregada para explicar as diferenças na dinâmica de crescimento dos países. Segundo sua teoria, existe uma relação positiva entre o crescimento da indústria e o crescimento do produto agregado, identificando a indústria como propulsora do crescimento por ser o setor mais dinâmico e inovador.

Logo após surgiu uma nova lei, conhecida como Kaldor-Verdoorn, na qual destaca a causalidade positiva da taxa crescimento da indústria de transformação na taxa de crescimento da produtividade industrial. Em seguida, surgiram uma terceira e uma quarta lei formulada por Kaldor (1970) e posteriormente revisada por Dixon e Thirlwall (1975), respectivamente sugerem que; quanto maior a taxa de crescimento das exportações, maior será o crescimento do produto; e que o crescimento da economia no longo prazo não é restringido pela oferta, mas sim pela demanda, portanto o crescimento das exportações seria fundamental para o crescimento regional.

Podem ser citados, similarmente, como modelos de crescimento regional, os modelos de aglomeração e economias de escala, teorias da dependência espacial e os modelos da nova geografia econômica, tais modelos diferenciam-se por incorporarem a dependência espacial. Os modelos de aglomeração e economias de escala tratam do efeito de transbordamento de conhecimento e tecnologia, assim como o menor custo de transporte e transações entre regiões vizinhas, os principais defensores dessa teoria são Marshall (1890), Arrow (1962) e Romer (1986).

Recentemente, a teoria da Nova Geografia Econômica, inicialmente apresentada por Krugman (1991), tem como foco o modelo centro-periferia, que foi revisado por Fujita, Krugman e Venables (2002) e Venables (1996), no qual sugere-se que os custos de transportes e mobilidade de fatores têm um papel fundamental na intensidade das aglomerações industriais.

Portanto, o presente estudo se pautará na investigação do grau de integração industrial estre os estados da região Sul do Brasil. De acordo com as teorias econômicas revisadas, podem ser observados diversos resultados, o que dependerá basicamente do tipo de bens produzidos e comercializados por esses estados, que poderá apontar ou para uma relação de abastecimento de insumos, efeitos complementares ou de espraiamento no mercado, ou efeitos de substituição ou concorrência, que se traduz em retardamento na atividade regional.

2.2. Evidências Empíricas

Diversos estudos foram realizados com vista a produzir evidências sobre a dinâmica do crescimento das regiões. Glaeser et al. (1992), utiliza dados do período de 1956 a 1987, de cidades e indústrias americanas, para examinar várias teorias sobre knowledge spillovers e explicar as tendências de aglomerações. A base de dados incorpora informações sobre empregos, salários e localização das companhias, e a estimação foi feita através de modelos cross-section de cidade-indústria incluindo variáveis explicativas de especialização e competição. A pesquisa conclui que as externalidades de conhecimento ocorrem com maior intensidade entre indústrias diversas do que dentro do mesmo setor.

Com o intuito de investigar a dispersão geográfica do parque industrial brasileiro, Diniz e Crocco (1996) utilizaram censos industriais do IBGE de 1970 a 1985, além de dados da Relação Anual de Informações Sociais – RAIS (Ministério do Trabalho) e PIB industrial, estimado pela Fundação de Economia e Estatística (FEE). No qual, a partir das distribuições das AIRs [4] em 1980, observa-se o efeito de espraiamento da indústria pelo país, aumentando-se a participação do Nordeste e diminuindo a do Sudeste e a do Sul em termos de AIRs. O Censo de 1991 apontou ainda para a existência do que foi denominado de polígono industrial com fronteiras entre Belo Horizonte (MG), Uberlândia (MG), Maringá (PR), São José dos Campos (SP), Porto Alegre (RS) e Florianópolis (SC). Os autores concluíram que o processo de desconcentração da geografia industrial que ocorreu no período 1970/91, não avançou nos primeiros anos desta década, permanecendo inalterada a participação do polígono industrial no total do emprego industrial. Contudo, no interior do polígono verificou-se a continuidade do processo de desconcentração, que se deu em grande parte em função de uma redução dos postos de trabalho em áreas industriais tradicionais, e não exclusivamente pela extensão de novas áreas industriais.

Em seguida, surgiram modelos inter-regionais de equilíbrio computável, com uma notória contribuição de Perobelli e Haddad (2006). Os autores implementaram um modelo interestadual de EGC no qual considera-se as três regiões brasileira: Norte, Nordeste e Centro-Sul. O autor destaca o papel das dinâmicas inter-regionais e interindustriais no desenvolvimento econômico, e concluem que a contribuição dos Estados do Rio Grande do Sul e Paraná para a variação do comércio inter-regional dos Estados da própria região situa-se acima dos 5%.

Posteriormente, Perobelli, Haddad e Domingues (2006) utilizaram uma matriz de insumo-produto inter-regional para 27 unidades da federação para o ano de 1996. Os autores chegaram à conclusão de que há um alto grau de interdependência intrarregional apresentados pelos estados do Sul e Sudeste, atestando, portanto, que maiores níveis de desenvolvimento podem estar relacionados com maiores níveis de comércio, principalmente comércio intraindústria.

Marque e Fochezatto (2012) realizaram um estudo empírico para os estados brasileiros com o objetivo de investigar se as diferenças econômicas entre as unidades federativas estão aumentando ou diminuindo nos últimos quarenta anos em termos de desenvolvimento econômico. Utilizando a análise de Cluster, chegam à conclusão de que as macrorregiões Norte-Nordeste e Sul-Sudeste individualmente estão convergindo, mas se consideradas em grupo, divergem entre si. Um aspecto peculiar foi que apenas os estados da região Sul se mantiveram no mesmo grupo de clusters nos diferentes períodos analisados, mostrando um maior nível de convergência econômica na região.

No intuito de adaptar teorias econômicas com modelos estatísticos surgiram vários modelos macroeconométricos. Os modelos inicialmente desenvolvidos seguiam a tradicional abordagem da Cowles Commission, tal sistema era fundamentado por centenas de equações e distinções entre variáveis endógenas e exógenas, que eram estimadas por mínimos quadrados ou pelo método de variáveis instrumentais. Porém, sérias críticas foram levantadas em relação ao modelo, principalmente a crítica de Lucas, que se tornou ultrapassado principalmente com o surgimento de modelos com vetores auto-regressivos (VAR), de Sims (1980).

 Rickman (2010) argumenta que, no que se refere aos modelos regionais, estes são construídos a partir de seus congêneres nacionais e, até o presente a metodologia macroeconométrica tem sido subutilizada por pesquisadores da área de economia regional. Portanto, o tratamento macroeconométrico baseado nos modelos DSGE e VAR/VEC globais ou VAR/VEC restritos, podem contribuir com respostas e evidências empíricas sobre os problemas inerentes dessa área.

Nesse sentido, Cromwell (1992) utiliza um modelo VAR para analisar a interação entre o estado da Califórnia e seus estados vizinhos observando até que ponto um choque na economia daquele afeta os seus vizinhos, utilizando dados trimestrais entre 1947 e 1991. Seus resultados mostram que o estado da Califórnia tem repercussões importantes nos demais estados, principalmente naqueles geograficamente mais próximos e que esses efeitos se mostram maiores no mercado de trabalho e na indústria.

Para o Brasil, o estudo de Tatiwa e Arruda (2011) apresentou pioneirismo na aplicação de modelos macroeconométricos numa perspectiva regional. O trabalho investiga a dinâmica industrial inter-regional a partir de funções de impulso resposta extraídas de um VAR com restrições nos parâmetros. Os resultados apontam para as regiões Sudeste e Sul como as propulsoras do crescimento industrial do país, enquanto que o Nordeste produz maiores efeitos de retardamento sobre as demais regiões do Brasil.

Posteriormente, visando entender melhor a dinâmica regional brasileira, Arruda e Tatiwa (2014) analisam a dinâmica industrial brasileira numa perspectiva intrarregional. As evidências encontradas sugerem uma predominância em curto prazo dos efeitos de rivalidade entre os estados do Ceará e de Pernambuco, no Nordeste, e entre os estados do Rio de Janeiro e de Minas Gerais, no Sudeste. Os autores desatacam ainda o Sul brasileiro como a região industrialmente mais integrada.

Buscando investigar se os efeitos de rivalidade em curto prazo observados por Arruda e Tatiwa (2014) permanecem em longo prazo, Arruda e Damasceno (2015) e Lima (2015) utilizam os vetores de correção de erro para examinar as interações industriais do Nordeste e Sudeste, respectivamente. Lima (2015) encontra evidências de longo prazo que apontam para maiores efeitos de espraiamento dos Estados de São Paulo e do Rio de Janeiro sobre Minas Gerais e Espírito Santo e destes sobre aqueles.  Entretanto, seus resultados indicam a existência de efeitos de retardamento entre São Paulo e Rio de Janeiro e Minas Gerais e Espírito Santo. Já Arruda e Damasceno (2015) indicam que o Estado da Bahia parece produzir os maiores efeitos positivos sobre o Nordeste, enquanto que Ceará e Pernambuco apresentam maiores efeitos retardamento entre si.

Assim, o presente estudo pretende contribuir com para a literatura supramencionada utilizando um vetor de correção de erros (VEC) de modo a examinar, além das relações de curto prazo, as elasticidades de longo prazo para a dinâmica industrial entre os estados Paraná, Rio Grande do Sul e Santa Catarina.

3.1. Descrição e Análise dos Dados

Para examinar as relações investigadas nesse estudo, são utilizados dados mensais entre janeiro de 1995 a fevereiro de 2014 do Índice de Produção Industrial – Indústria Geral – (IPI), em nível estadual, para Paraná, Rio Grande do Sul e Santa Catarina. O quadro abaixo apresenta uma síntese das variáveis utilizadas.

Para subsidiar a análise econométrica aqui executada e obter fatos que possam contribuir com informações qualitativas para os resultados obtidos por esse estudo, procedeu-se uma investigação descritiva da dinâmica industrial desses estados sob a ótica das exportações e importações. Inicialmente, analisou-se a composição das exportações e importações dessa região pela definição de fator agregado, qual seja, básicos e industrializados. Os dados foram obtidos com a Secretaria de Comércio Exterior, do Ministério do Desenvolvimento, Indústria e Comércio Exterior (SECEX/MDIC). A Tabela 1 apresenta uma síntese dessas informações.

Percebe-se, primeiramente, uma participação majoritária de bens industrializados tanto nas importações como nas exportações de todos os estados da região Sul, com destaque para Paraná e Rio Grande do Sul nas exportações de produtos da indústria, com 64,55% e 62,29%, respectivamente.

Analisando a taxa de crescimento média da participação dos básicos e dos industrializados nas exportações, observa-se que, entre 1995 a 2014, todos os estados da região apresentaram retração média na exportação de industrializados, com Rio Grande do Sul e Santa Catarina apresentando as maiores perdas médias, 1,74% a.a. e 1,13% a.a., respectivamente. Essa evidência pode ser explicada pela redução recente dos preços de commodities agropecuárias no mercado internacional. 

Em se tratando de exportações de produtos básicos, observaram-se expansões médias anuais em todos os estados, com Rio Grande do Sul e Santa Catarina se destacando com maiores taxas de crescimento médio, 2,52% a.a. e 1,85% a.a., respectivamente.

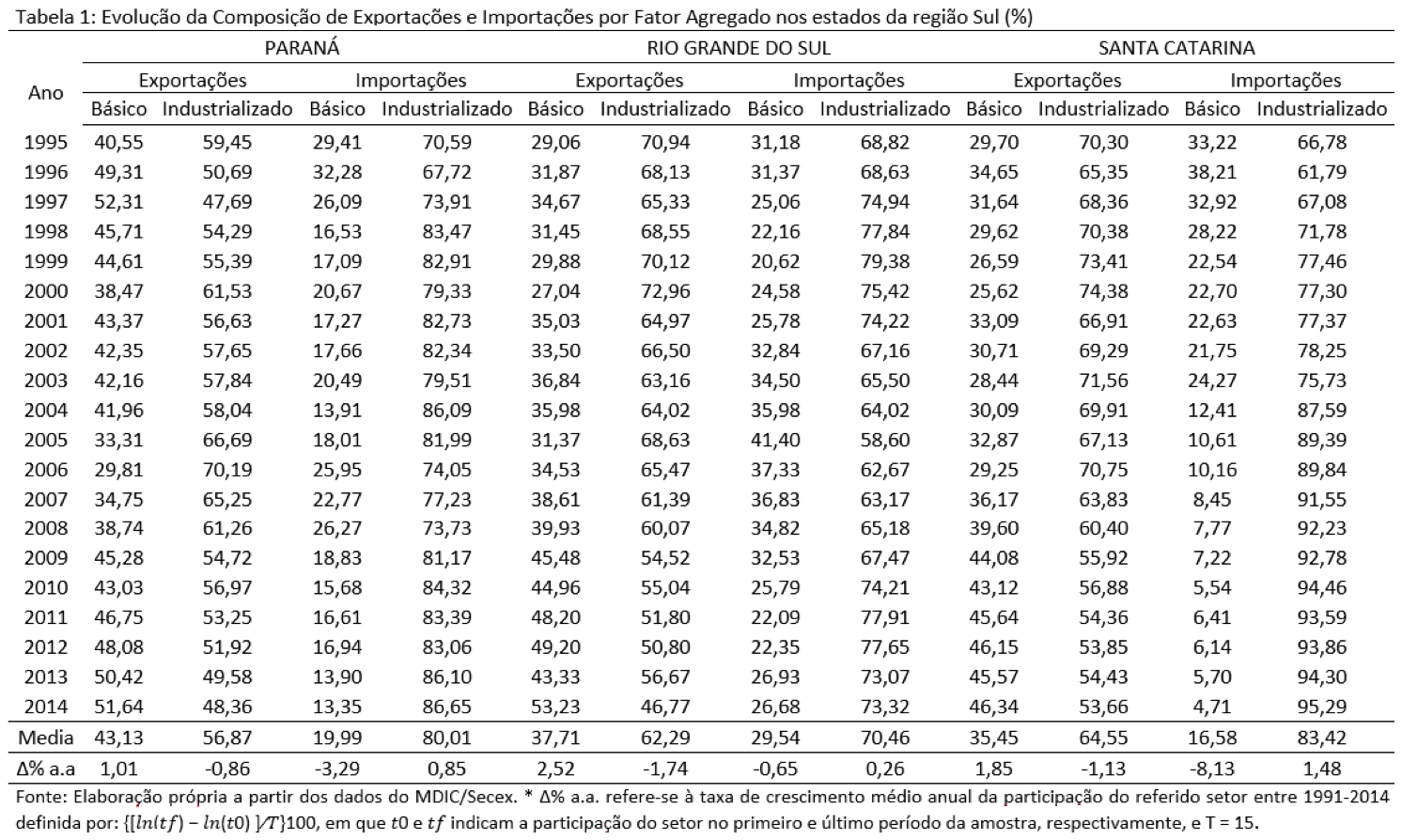
Analisando a evolução das importações por fator agregado, percebe-se também uma participação majoritária de produtos da indústria nos três estados.  Santa Catarina e Paraná apresentaram maiores participações médias, 83,42% e 80,01%, respectivamente. Ainda, o Estado de Santa Catarina, além de apresentar maior participação média de industrializados em sua pauta de importações, também apresentou a maior taxa de crescimento média anual das importações desse setor, na ordem de 1,48%, entre 1995 e 2014.

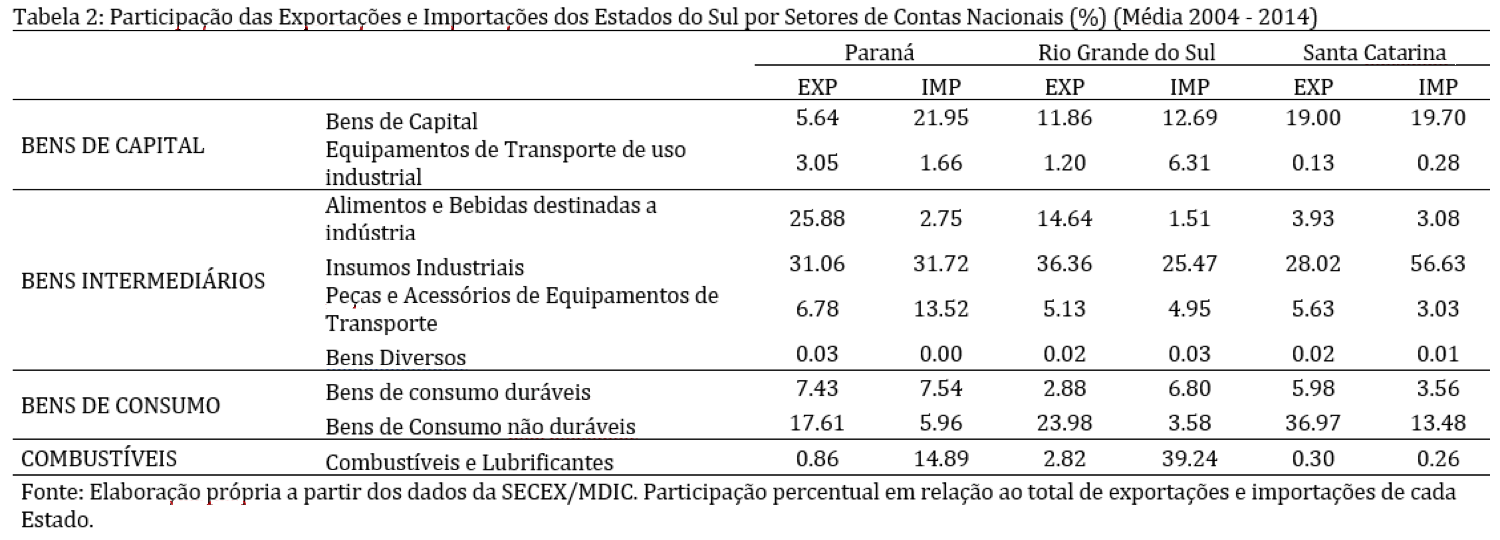
Adicionalmente, examinou-se também a participação das exportações e importações dos estados da região Sul por setores de contas nacionais: bens de capital, bens intermediários, bens de consumo e combustíveis e lubrificantes. Os dados estão sintetizados na tabela 2.

Nota-se que, em todas as unidades federativas analisadas, há uma participação majoritária no percentual de exportação e importação de bens intermediários, porém Santa Catarina destaca-se pela proporção de insumos industriais importados (56,63%) e pela exportação de bens de consumo não duráveis (36,97%). No Rio Grande do Sul chama a atenção a grande quantidade de combustíveis e lubrificantes importados (34,29%), quanto à exportação, os insumos industriais matem a maior proporção (36,36%). Por fim, o Paraná mostra-se como um exportador principalmente de insumos industriais (31,06%) e de alimentos e bebidas destinados à indústria (25,88), assim como importador de insumos industriais (31,72%) e bens de capital (21,95%).

Analisando a atuação em setores a de alto valor agregado, os estados de Santa Catarina e Rio Grande do Sul apresentam destaque como os maiores exportadores de bens de capital da região, com participações médias de 19% e 11,86%, respectivamente.

3.2. Estratégia Econométrica

A análise das interações de curto e de longo prazo na indústria da região Sul do Brasil será conduzida a partir a utilização da técnica de cointegração multivariada proposta por Johansen (1988).

Intuitivamente, diz-se que duas ou mais séries são cointegradas se estas apresentam um comovimento ao longo do tempo e suas diferenças são estacionárias, embora cada série específica seja não estacionária; ou seja, essa definição indica a existência de um equilíbrio em longo prazo na relação entre essas variáveis. Desta maneira, a análise de cointegração se mostra uma ferramenta adequada para o exame das relações investigadas nesse estudo. Tecnicamente, duas ou mais séries que são, por exemplo, integradas de ordem 1, I(1), e, portanto, não estacionárias, são consideradas cointegradas se existir uma combinação linear delas que seja estacionária, I(0), e o vetor que propicia essa série I(0) é chamado de vetor de cointegração.

Portanto, quando as séries não são I(0), os resíduos podem não ser estacionários e a estimação por mínimos quadrados pode produzir resultados espúrios. Desta forma, é necessário certificar-se de que os resíduos do sistema são estacionários ou, ainda, se podem ser estacionarizados, de modo a tornar possível a estimação. Portanto, se um vetor de variáveis, possui um equilíbrio de longo prazo, isto é, se elas são cointegradas, é possível encontrar uma combinação linear entre esse vetor e um vetor β, denominado vetor de cointegração, de modo que os resíduos do sistema sejam estacionários. Assim, a cointegração existe se for possível encontrar um vetor Z_t=〖β'Y〗_t tal que Z_t seja I(0).

Em que o vetor Yt inclui as variáveis de produção industrial, em logaritmos, dos estados do Paraná (LN_IPI_PR), Rio Grande do Sul (LN_IPI_RS) e Santa Catarina (LN_IPI_SC).

Portanto, inicialmente analisar-se-á ordem de integração das variáveis. Para tal, faz-se uso dos testes de Dickey-Fuller aumentado (ADF), que têm a presença de raiz unitária como hipótese nula e, de modo a complementar esses resultados e robustecer essa análise, emprega-se também o teste de Kwiatkowski, Phillips, Schmidt e Shin (KPSS), sob a hipótese nula de estacionariedade. Uma vez que as séries não se mostrem estacionárias, procede-se a investigação da existência de relação de longo prazo entre as variáveis e a quantidade de vetores de cointegração, utilizando-se os testes do traço e do máximo autovalor que indicam a existência de relação de longo prazo entre as variáveis e a quantidade de vetores de cointegração, nos moldes sugeridos por Johansen (1988). Após a identificação dos vetores de cointegração, procede-se a estimação do VEC.

As repercussões de curto prazo são extraídas a partir da análise da decomposição de variância do erro de previsão e das funções de impulso resposta (FIR) do modelo VAR estimado, em sua versão generalizada. Vale destacar que o uso da FIR generalizada se justifica pelo fato de que esta não se altera com a reordenação de variáveis no VAR.

Lutkepohl (1991) argumenta que o método tradicional para a análise das FIR aplica a “hipótese da ortogonalidade”, o que, consequentemente, faz com que o resultado dependa da ordenação das séries no VAR. Koop, Pesaran e Potter (1996), e Pesaran e Shin (1998) desenvolveram a FIR generalizada como forma de eliminar o problema de ordenação das variáveis no VAR. Já as interações de longo prazo serão extraídas a partir da análise dos vetores de cointegração.

Em suma, a estratégia econométrica empregada nesse estudo pode ser assim resumida: após a investigação da ordem de integração das séries e a verificação de existência de cointegração entre as variáveis em estudo, procede-se à estimação de um VEC, de onde são extraídas as relações de curto e de longo prazo examinadas nesse trabalho.

Para analisar e quantificar as relações de curto e de longo prazo na indústria da região Sul do Brasil, inicialmente foi realizada uma análise da ordem de integração das variáveis. Os testes ADF e KPSS foram aplicados com as variáveis em nível e em primeira diferença e seus resultados constam na tabela 3.

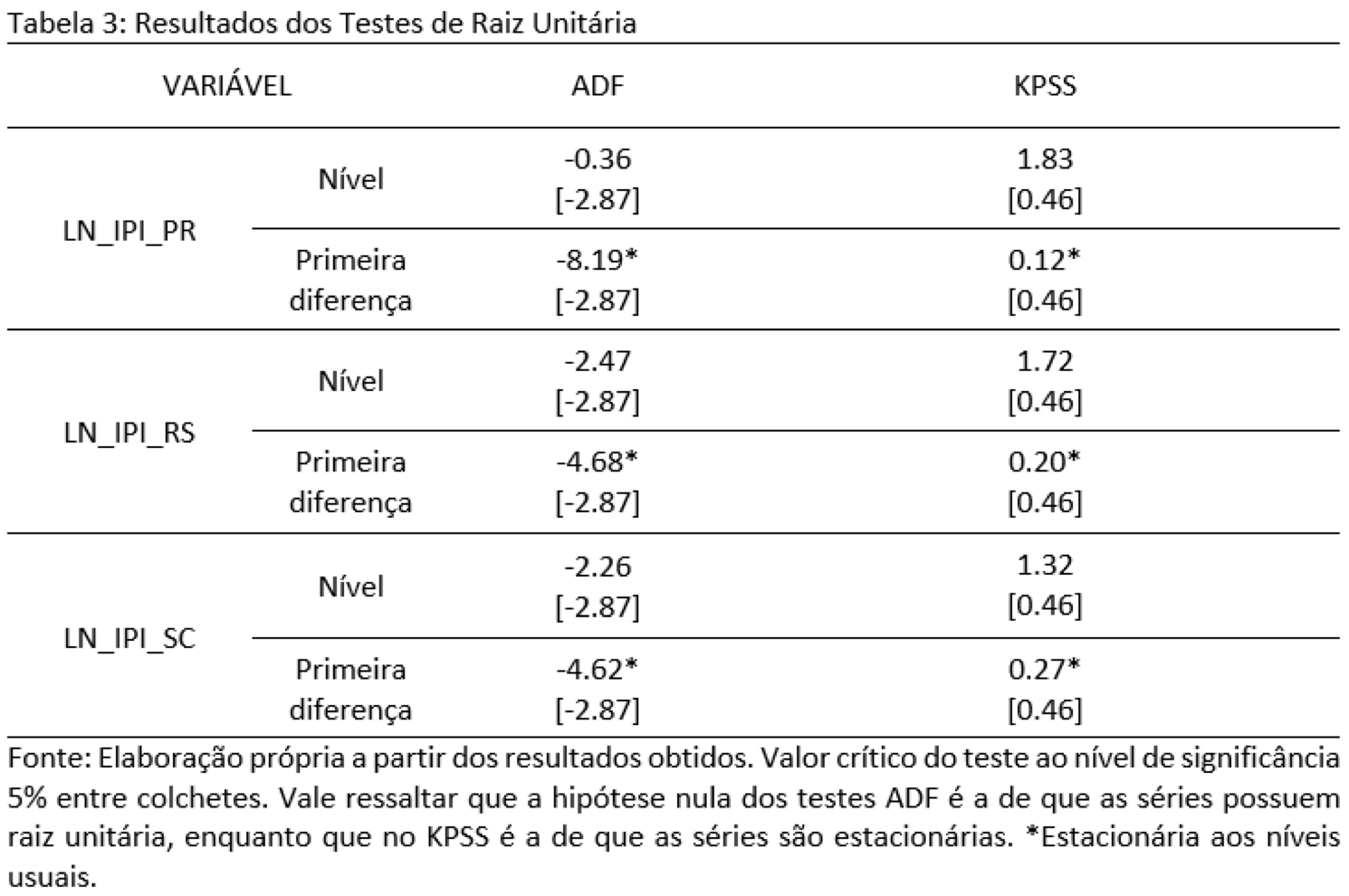
Os resultados apontam que todas as séries utilizadas no presente trabalho se mostram integradas de ordem um, isto é, I(1). Diz-se que uma série temporal é integrada de ordem d, sendo representada como Y_t~I(d), se a série é não estacionária, mas pode ser transformadas em uma série estacionária após d diferenças.

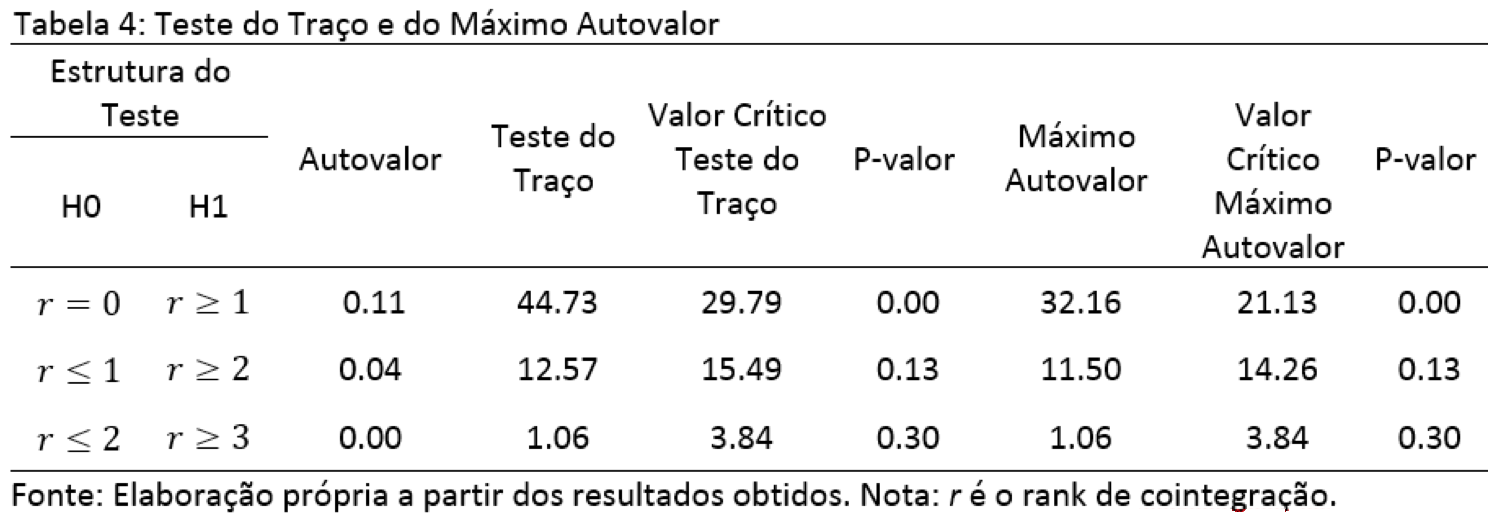
Após essa constatação, empregou-se os testes de traço e de máximo autovalor para a análise de cointegração entre essas variáveis. Os resultados estão sintetizados na tabela 4 e indicam a existência de um vetor de cointegração, ou relação de longo prazo, entre as séries empregadas. Adicionalmente, o Critério de Schwarz (CS) indicou dois como o número ótimo de defasagens do VAR; ou seja, o modelo empregado nesse estudo será representado como VEC (1). As subseções seguintes discutem os resultados para as dinâmicas de curto e de longo prazo.

4.1. Dinâmica de Curto Prazo

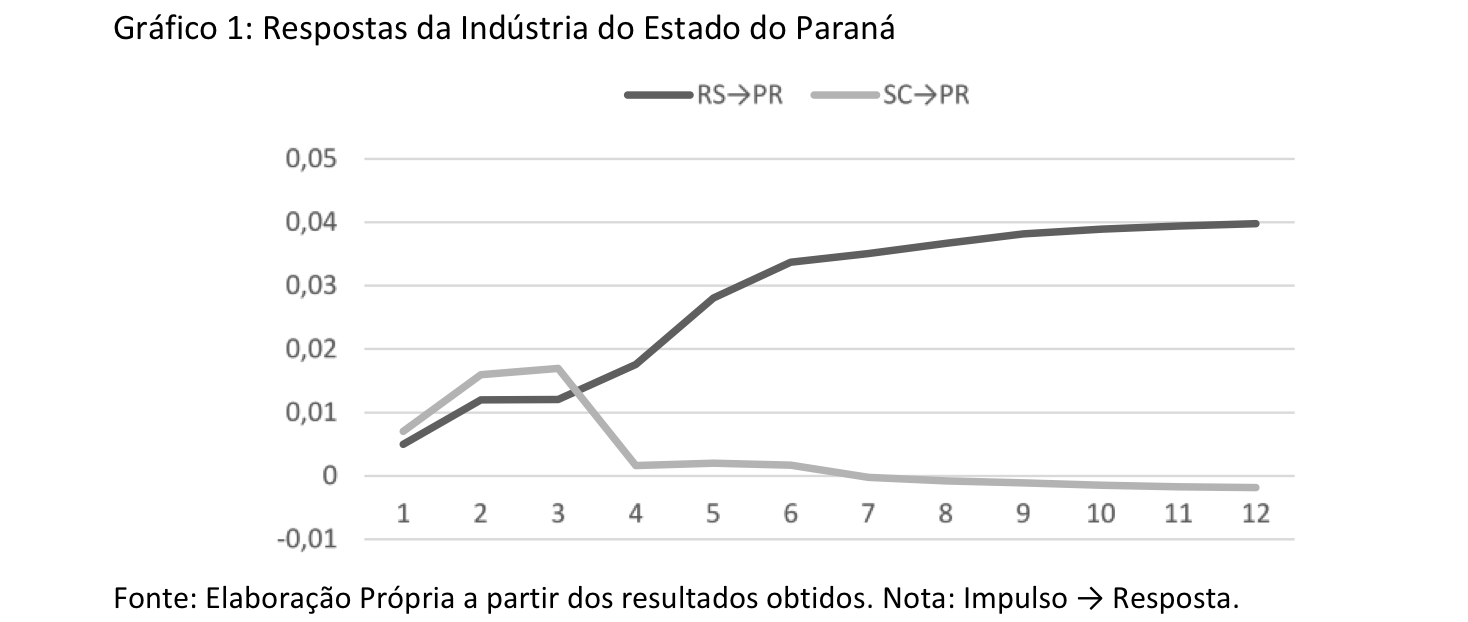
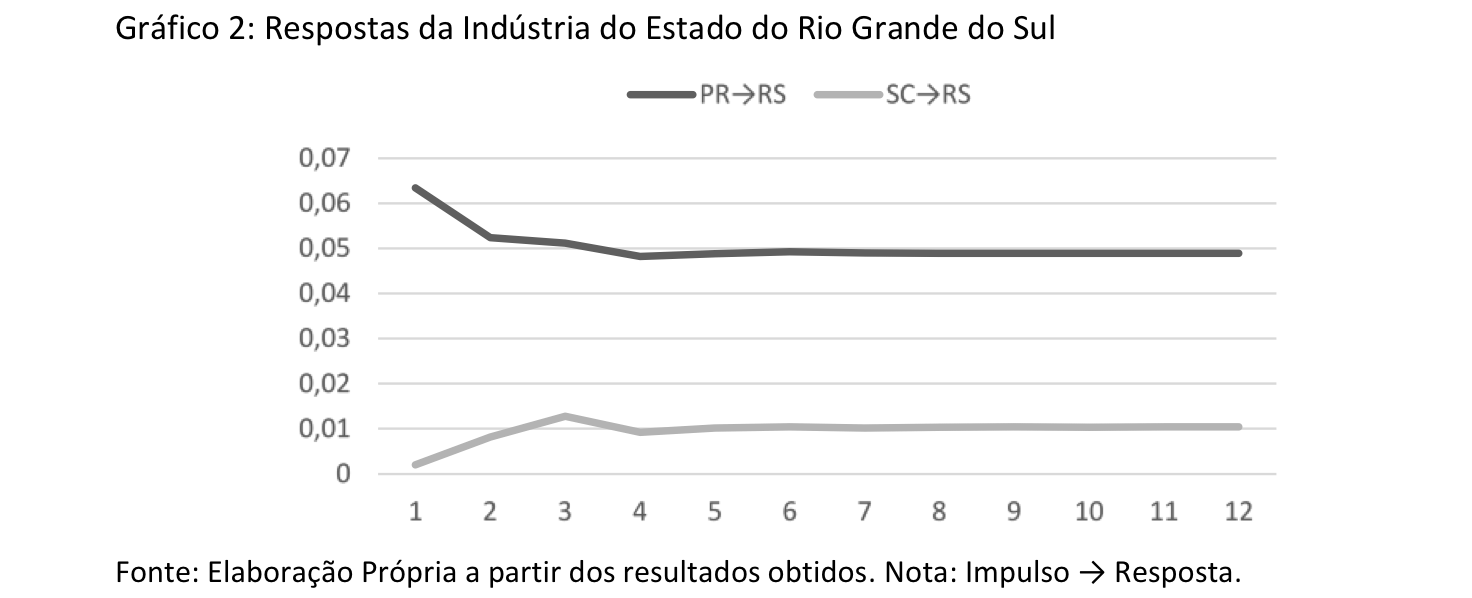
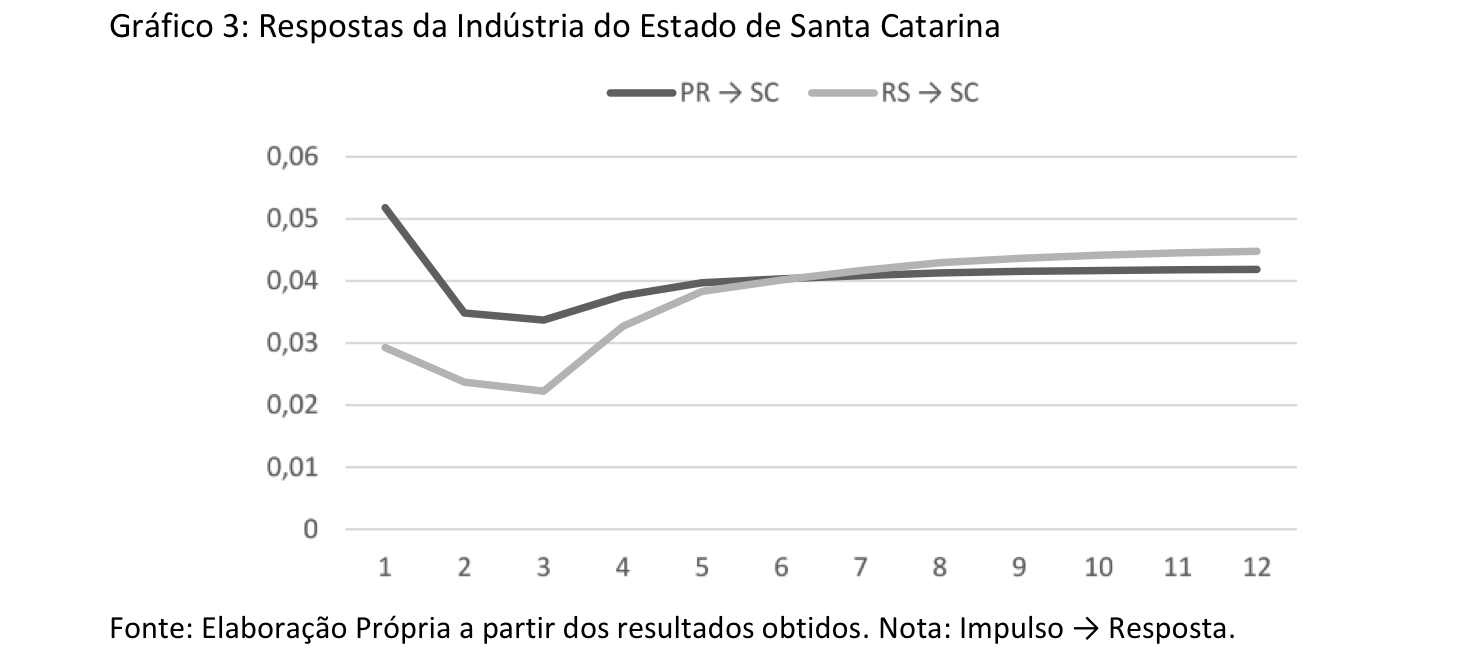
As relações de curto prazo da indústria da região Sul são examinadas a partir das FIR Generalizadas e da Decomposição de Variância do Erro de Previsão (DV). Os gráficos 1 a 3 apresentam os resultados das FIR. A primeiro gráfico apresenta as respostas da indústria do Paraná a choques no Rio Grande do Sul e Santa Catarina. Em seguida, no gráfico 2, observam-se as respostas de atividade industrial do Rio Grande do Sul às oscilações na indústria de Paraná e Santa Catarina. Por fim, o ultimo gráfico expõe as respostas para a indústria catarinense.

Em termos gerais, os resultados revelam que os choques na atividade industrial de qualquer estado da região Sul apresentam repercussões de curto prazo positivas, uma vez que as todas as FIR presentes nos gráficos 1 a 3 apontam para impactos positivos. Vale destacar que as repercussões mais intensas, em termos de magnitude, na indústria dos estados da região Sul foram observadas em resposta à choques na atividade industrial do Estado do Paraná.

Portanto observa-se um importante efeito de espraiamento de curto prazo entre as indústrias dos estados da região Sul do Brasil. Resultados semelhantes foram destacados por Arruda e Tatiwa (2014), que apontam para uma importante integração industrial entre os estados do Paraná e do Rio Grande do Sul. Vale destacar que esses autores não incluem Santa Catarina em sua análise.

----

----

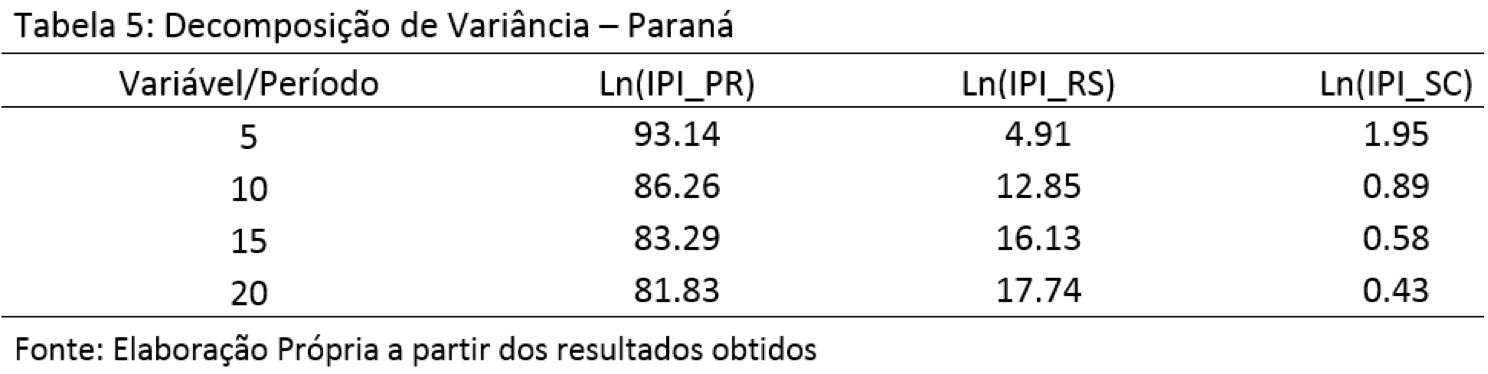
Ainda numa perspectiva de curto prazo, foi realizada a investigação da Decomposição da Variância do Erro de Previsão (DV). Em termos gerais, percebe-se uma forte interação industrial entre os estados estudados, com exceção do Estado do Paraná, que parece apresentar uma dinâmica mais independente.

A Tabela 5 descreve a DV para o estado do Paraná. Os resultados indicam que, para previsões de cinco períodos à frente, a variância de seus erros de previsão é explicada em 4.91% pela dinâmica industrial do Rio Grande do Sul e em apenas 1.95% pela atividade industrial catarinense. Essas participações, para previsões de 20 períodos à frente, são de 17.74% e 0.43% para Rio Grande do Sul e Santa Catarina, respectivamente; ou seja, no curto prazo a produção industrial do Paraná se mostra pouco dependente dos demais estados de sua região.

Considerando o Estado do Rio Grande do Sul, representado na Tabela 6, a variância dos erros de previsão, para cinco períodos à frente, é explicada em 55.87% e 1.65%, pela dinâmica dos estados do Paraná e Santa Catarina, respectivamente. Ou seja, os erros de previsão da atividade industrial do Rio Grande do Sul são fortemente explicados por variações na indústria paranaense. Para previsão de 20 períodos à frente, Paraná é responsável por 58.02% das variações na dinâmica industrial gaúcha, enquanto a indústria catarinense a afeta em 2.36%.

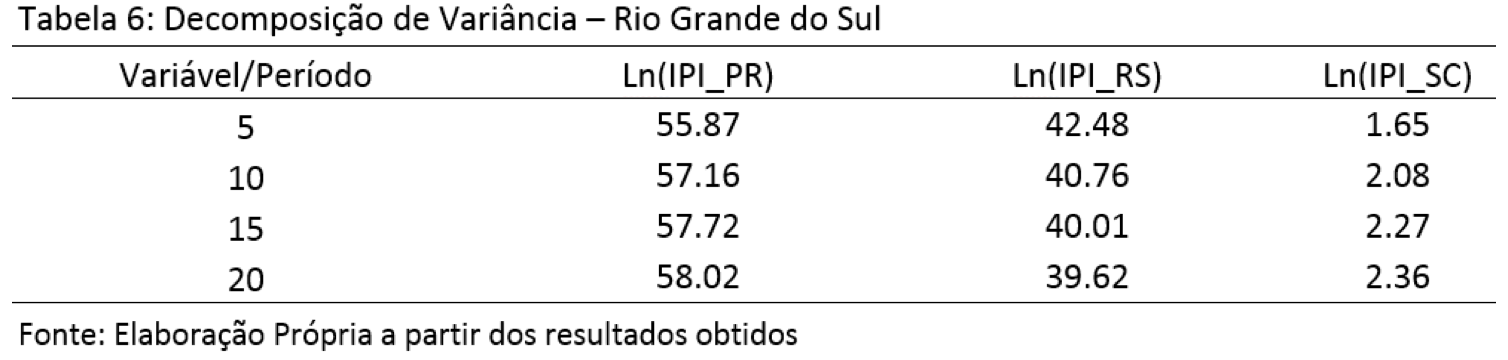
Por fim, a tabela 7 destaca os resultados da DV para o Estado de Santa Catarina. As evidências indicam que, num horizonte de cinco períodos a frente, a explicação de seus erros de previsão é representada em 47.55% pela dinâmica industrial do estado do Paraná e 26.36% pela indústria gaúcha; para previsões de 20 períodos a frente, a indústria paranaense explica 43.78%, enquanto que a dinâmica industrial gaúcha afeta 43.33% das variações do erro de previsão da atividade industrial de Santa Catarina; ou seja, esse resultado mostra que a indústria catarinense é fortemente afetada por seus estados vizinhos no curto prazo e se mostra menos independente.

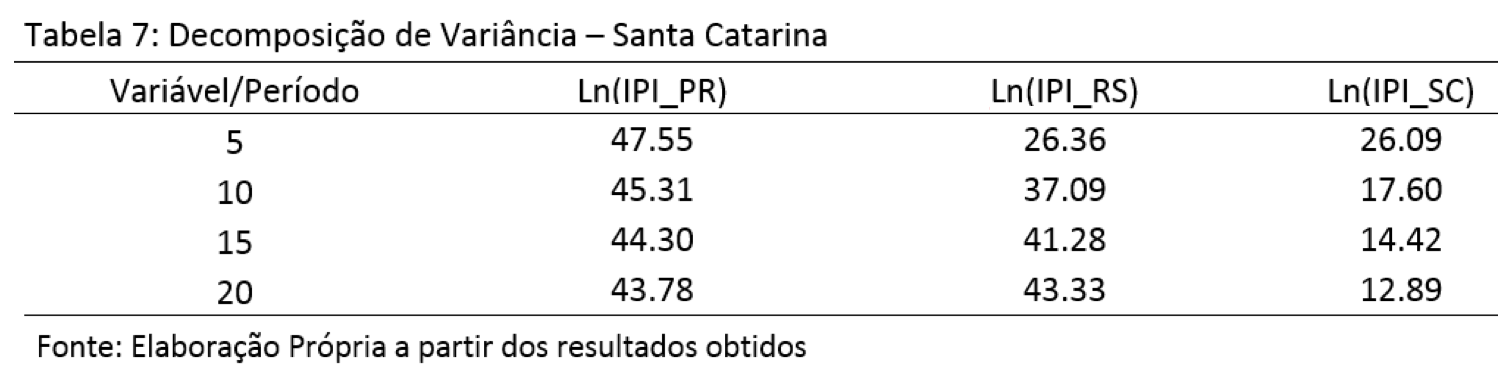
Em suma, os resultados de curto prazo fornecidos pela DV parecem indicar que: i) a indústria do Paraná parece apresentar o maior grau de independência em relação aos demais estados, além de explicar as maiores porções das variações dos erros de previsões de seus vizinhos; ii) a indústria gaúcha mostra-se mais afetada pela do Paraná, resultado também destacado por Arruda e Tatiwa (2014); iii) a dinâmica industrial de Santa Catarina se mostrou mais dependente, em termos de variações em seus erros de previsão, em relação à Paraná e Rio Grande do Sul.

4.2. Dinâmica de Longo Prazo

As relações de longo prazo entre as indústrias dos estados do Sul brasileiro foram examinadas a partir do vetor de cointegração estimado, e os resultados estão dispostos na tabela 8. Deve-se observar que os valores dos coeficientes estimados estão normalizados para a variável em questão, indicada pela linha da tabela, e que seus sinais já se encontram invertidos na tabela. Em termos gerais, todos os coeficientes estimados se mostraram estatisticamente significantes aos níveis usuais.

Os resultados mostram que, majorando em 1% a produção industrial do Estado do Rio Grande do Sul, a indústria do Paraná e de Santa Catarina se expandirá em 3.12% e 1.71%, respectivamente; ou seja, os impactos positivos da indústria gaúcha sobre os demais estados da região Sul parecem permanecer no longo prazo e se mostram elásticos, apontando que o Estado do Rio Grande do Sul produz as maiores repercussões sobre os demais estados de sua região.

A mesma análise para o Paraná releva que a indústria gaúcha crescerá em 0.31% e a produção industrial catarinense sofrerá retração de 0.55%, em resposta a um aumento de 1% da produção da indústria paranaense. Ou seja, em longo prazo, o Estado do Paraná produz maiores efeitos de espraiamento sobre o Rio Grande do Sul e maiores efeitos retardamento sobre Santa Catarina; noutros termos, a indústria paranaense parece produzir um efeito rival em relação à de Santa Catarina. Essa rivalidade pode ser explicada pelo fato de que a indústria desses dois estados está bem concentrada em bens de consumo não duráveis, ver tabela 2; ou seja, quando a atividade industrial de uma aumenta, a demanda por bens de consumo não duráveis da outra é reduzida ocasionando um efeito rival negativo.

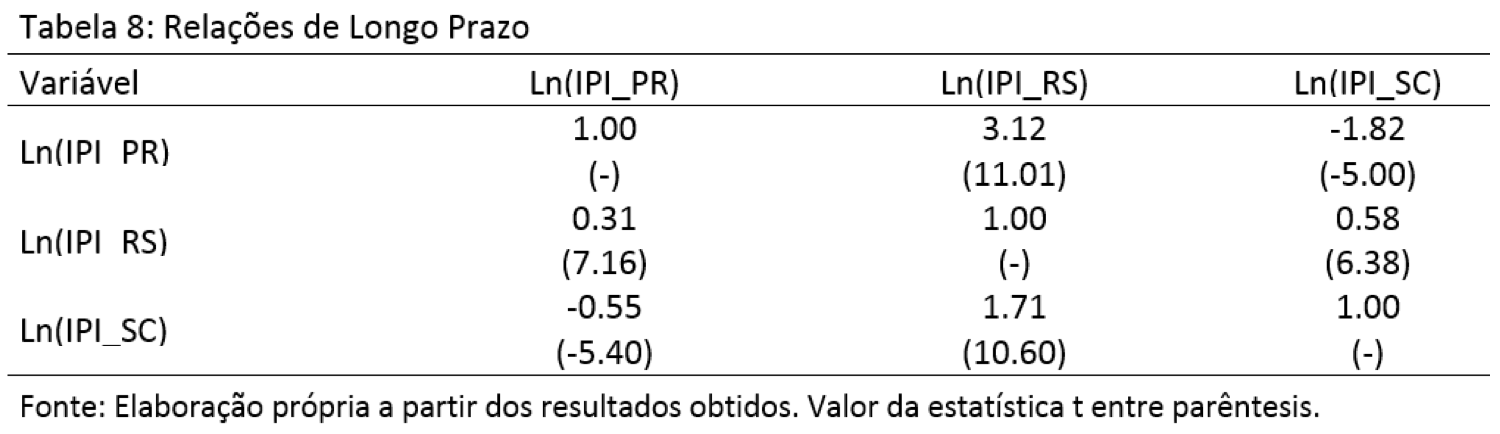
Por fim, a relação de longo prazo para o estado de Santa Catarina indica que um incremento de 1% em sua produção industrial tem como consequência um impacto positivo na indústria gaúcha da ordem de 0.58% e uma repercussão negativa na ordem de 1.82% na indústria do estado do Paraná. Isto é, em longo prazo, o Estado de Santa Catarina parece rivalizar apenas com o Paraná, mas contribui para o crescimento da indústria gaúcha. Tal rivalidade entre Santa Catarina e Paraná pode ser explicada como no parágrafo anterior, através da tabela 2.

Portanto, as evidências de longo prazo indicam que o estado do Rio Grande do Sul apresenta os resultados positivos mais elásticos sobre as indústrias dos demais estados, em especial sobre o estado do Paraná. A indústria paranaense apresenta impactos de longo prazo positivos para a indústria gaúcha e negativos para a indústria catarinense. Já Santa Catarina apresenta impacto positivo sobre o Estado do Rio Grande do Sul e negativo e elástico sobre o Paraná.

O presente estudo examinou as dinâmicas de curto e de longo prazo entre as indústrias dos estados da região Sul do Brasil com dados mensais entre janeiro de 1995 e fevereiro de 2014 e vetores de correção de erros.

Em termos gerais, a dinâmica de curto prazo via FIR destacou-se por apresentar impactos positivos de curto prazo entre todos os estados, indicando uma forte integração na região Sul e maiores efeitos de espraiamento, com o estado do Paraná gerando os maiores impactos sobre os demais estados, corroborando com os achados de Arruda e Tatiwa (2014).

Em se tratando da decomposição de variância dos erros de previsão, o resultado se mostra o estado de Santa Catarina como o mais dependente da região, em termos de atividades industriais, pois ao longo do tempo a variância do seu erro de previsão é bastante influenciada pelos demais estados do Sul. Conclui-se também que: i) as variações na atividade industrial de Santa Catarina influenciam pouco os estados Paraná e Rio Grande do Sul; ii) o Paraná se mostra o estado mais independente da região em termos de choques industriais; iii) A indústria do Rio Grande do Sul e do Paraná apresentam maiores efeitos de espraiamento, havendo uma convergência maior entre os dois estados, resultado semelhante ao observado por Arruda e Tatiwa (2014).

Por fim, as elasticidades de longo prazo apontam que: i) Elevando em 1% a produção industrial do Estado do Rio Grande do Sul, a indústria do Paraná e de Santa Catarina se expandirá em 3.12% e 1.71%, respectivamente; ii) Um aumento de 1% da produção industrial paraense acarreta um crescimento de 0.31% na indústria gaúcha e a produção industrial catarinense sofrerá retração de 0.55%; iii) Se o aumento ocorre em Santa Catarina haveria um impacto positivo na indústria gaúcha da ordem de 0.58% e uma repercussão negativa na ordem de 1.82% na indústria do estado do Paraná.

 Além disso, no longo prazo, a atividade industrial do Rio Grande do Sul tem maior elasticidade positiva nos demais estados; e a indústria de Santa Catarina e Paraná parece rivalizar ao longo do tempo, sendo observado um maior efeito de retardamento entre os dois estados, já que a indústria de ambos está bem concentrada em bens de consumo não duráveis.

Assim, conclui-se que uma política de incentivo ao desenvolvimento na região Sul do Brasil, através da expansão da produção industrial, deve levar em consideração evidências como as apresentadas nesse estudo, a fim de que se possa obter um resultado ótimo para todos os estados da região, minimizando os efeitos de rivalidade e maximizando os ganhos de escala oriundos da proximidade geográfica.

ARROW, K. J. (1962). The economic implications of learning by doing. Review of Economic Studies. Oxford University Press, v. 29, n. 3, p. 155–173, jun.

ARRUDA, E. F.; TATIWA, R. (2014). Dinâmica Intrarregional do Brasil: Quem dirige o crescimento industrial das regiões brasileiras? Economia Aplicada. Ribeirão Preto, v. 18, n. 2, p. 243-270, apr./jun.

ARRUDA, E. F. e DAMASCENO, V. C. (2015). Relações de Curto e Longo Prazo na Indústria do Nordeste Brasileiro. Revista Ciências Administrativas.  v. 21, nº 1, p. 184-210.

CROMWELL, B. A. (1992). Does California Drive the West? An Econometric Investigation of Regional Spillovers. Economis Review Federal Reserve of San Francisco, San Francisco- Calif., nº 2, p. 12-23.

DINIZ, C. C.; CROCCO, M. A. (1996). Reestruturação econômica e impacto regional: o novo mapa da indústria brasileira, Nova Economia, v. 6, nº 01, p. 77-103.

DIXON, R.; TRILWALL, A. (1975). Model of Regional Growth-Rate Differences on Kaldorian Lines. Oxford Economic Papers, Oxford, v. 21, nº 2, July.

EWING, B. T. (2003). The response of the default risk premium to macroeconomic shocks. The Quarterly Review of Economics and Finance, Champaign, v. 43, nº 2, p. 261-272.

FUJITA, M.; KRUGMAN, P.; VENABLES, A. Economia espacial. São Paulo: Futura.

GLAESER, E. L.; KALLAL, H.; SHEINKMAN, J.; SCHLEIFER, A. (1992). Growth in cities, Journal of Political Economy, v. 100, p. 1126-1152.

HIRSCHMAN, A. (1975). The Strategy of Economic Development, Yale University Press.

JOHANSEN, S. (1988). Statistical Analysis of Cointegration Vectors. Journal of Economic Dynamics and Control, Columbia, v. 12, n. 2-3, p. 231-254, Jun./Set.

KALDOR, N. (1970). The Case for Regional Policies. Scottish Journal of Political Economy, Aberdeen, v. 17, n. 3, p. 337-348, nov.

KOOP, G.; PESARAN, M. H.; POTTER, S. M. (1996). Impulse response analysis in non-linear multivariate models. Journal of Econometrics, v. 74, n. 1, p. 119–147, Sep.

KRUGMAN, P. (1991). Geography and Trade. Cambridge, MA: MIT Press.

Lima, D. C. Q. (2015). Repercussões de Curto e Longo Prazos na Indústria do Sudeste Brasileiro. Monografia (Graduação em Ciências Econômicas) - Faculdade de Economia, Administração, Atuária e Contabilidade, Universidade Federal do Ceará - Universidade Federal do Ceará, Fortaleza.

LÜTKEPOHL, H. (1991). Introduction to multiple time series analysis. Berlin: Springer.

LÜTKEPOHL, H.; KRÄTZIG, M. (2004). Applied Time Series Econometrics. New York: Cambridge University Press.

MARQUES, A. M; FOCHEZATTO, A. (2012) Desenvolvimento convergente ou divergente entre os estados brasileiros? Uma análise multidimensional, 1970-2000, In: ENCONTRO DE ECONOMIA DA REGIÃO SUL,15., 2012. Porto Alegre. Anais...Porto Alegre: ANPEC.

MARSHALL, A. (1890). Principles of Economics. 8th. ed. London: Macmillan.

MYRDAL, G. (1963). Economic Theory and Underdeveloped Regions. London: Methuen.

PEROBELLI, F. S.; HADDAD, E. A. (2006). Padrões de Comércio Interestadual no Brasil, 1985 e 1997. Revista Econômica Contemporânea, Rio de Janeiro, v. 10, n. 1, p. 61-88, jan./Abr.

PEROBELLI, F. S.; HADDAD, E. A.; DOMINGUES; E. P. (2006). Interdependence among the Brazilian

States: an input-output approach. In: ENCONTRO NACIONAL DE ECONOMIA, 34., 2006. Salvador, BA. Anais...Salvador/BA: ANPEC.

PESARAN, M. H.; SHIN, Y. (1998). Generalized impulse response analysis in linear multivariate models. Economic Letters, San Francisco, v. 58, n. 1, p. 17-29, Jan.

RICKMAN, D. S. (2010). Modern macroeconomics and regional economic modeling. Journal of Regional Science, v. 50, nº 1, p. 23–41, Feb.

ROMER, P. (1986). Increasing returns and long-run growth. Journal of Political Economy, Chicago, v. 94, n. 5, p. 1002–1037, Oct.

SIMS, C. (1980). Macroeconomics and Reality. Econometrica, v. 48, n. 1, p.1-48, Jan.

TATIWA, R. F.; ARRUDA, E. F. (2011). Dinâmica da atividade industrial brasileira e seus spillovers regionais e externos. In: Encontro Nacional de Economia, XXXIX, 2011, Foz do Iguaçu. Anais… Foz do Iguaçu: ANPEC, p.1-19.

WILLIAMSON, J. (1965). Regional inequality and the process of national development. Economic Development and Cultural Change, Chicago, v. 13, n. 4, Part 2, p. 1-84, jul.

________________(1977). Desigualdade regional e o processo de desenvolvimento nacional: descrição dos padrões, In: SCHWARTZMAN, J. (Org.) Economia regional: textos escolhidos. Belo Horizonte: Editora UFMG, 1977.

VENABLES A. J. (1996), Equilibrium locations of vertically linked industries, International Economic Review, v. 37, nº 2, p. 341-359.

1. Doutor em Economia. Professor do Programa de Pós Graduação em Economia (CAEN/UFC) e do Mestrado Acadêmico em Economia Rural (MAER/UFC). E-mail: elano@ufc.br

2. Bacharel em Finanças pela Universidade Federal do Ceará. E-mail: andressapaivac@gmail.com

3. Doutor em Economia. Professor do Curso de Finanças da Universidade Federal do Ceará. E-mail: pcastelar@ufc.br

4. IBGE: microrregiões homogêneas, que segundo os Censos Demográficos de 1970, 1980 e 1991 possuíam 10 mil ou mais pessoas ocupadas nas indústrias.