

 Vol. 38 (Nº 45) Año 2017. Pág. 35
Vol. 38 (Nº 45) Año 2017. Pág. 35
Gaukhar OMASHOVA 1; Roza SPABEKOVA 2; Kenzhekhan KABYLBEKOV 3; Nurila SAIDULLAYEVA 4; Pulat SAIDAKHMETOV 5; Saltanat DJUNUSBEKOVA 6
Recibido: 09/08/2017 • Aprobado: 15/08/2017
3. Methodical recommendations for task fulfillment
4. Control questions for checking students' readiness for work
ABSTRACT: This paper presents the model of a blank form for the organization of computer laboratory work on studying the engine making a Carnot cycle, including short theoretical data, introductory assignments with the computer model, tasks with the subsequent computer checkout of answers, ambiguous tasks as well as experimental, research and creative tasks. Brief theoretical data define a thermal engine and describe the principle of its operation, the processes of a Carnot cycle, the coefficient of performance of a thermal engine, the operation of a cooler and some controversial issues on explaining the efficiency of direct and reverse Carnot cycles. Introductory tasks with the computer model include questions related to the ability to change the parameters (pressure and temperature) of processes and to determine the volume of the working substance, taking into account the possibility of the model. The fulfillment of tasks with the subsequent computer checkout of answers provides for their preliminary solution on paper, the implementation of the conditions of tasks in the computer experiment, the verification of answers and the presentation of the results of solving tasks on paper along with the blank. Experimental tasks include the implementation of the specified parameters on the computer model, the definition of the work, heat and efficiency of an engine. Ambiguous tasks require finding the temperatures of a heater and a cooler for achieving a given coefficient of performance. Research tasks include a number of issues on increasing the coefficient of performance of an engine. |
RESUMEN: En este trabajo se presenta el modelo de una forma en blanco para la organización de trabajos de laboratorio informático sobre el estudio del motor que hace un ciclo de Carnot, incluyendo datos teóricos cortos, asignaciones introductorias con el modelo de ordenador, tareas con el ordenador posterior retirada de respuestas, tareas ambiguas así como tareas experimentales, de investigación y creativas. Los datos teóricos breves definen un motor termal y describen el principio de su operación, los procesos de un ciclo de Carnot, el coeficiente de funcionamiento de un motor termal, la operación de un refrigerador y algunas ediciones polémicas en explicar la eficacia de ciclos directos e inversos de Carnot. Las tareas introductorias con el modelo informático incluyen cuestiones relacionadas con la capacidad de cambiar los parámetros (presión y temperatura) de los procesos y determinar el volumen de la sustancia de trabajo, teniendo en cuenta la posibilidad del modelo. El cumplimiento de las tareas con la posterior comprobación de las respuestas por computadora proporciona su solución preliminar en papel, la implementación de las condiciones de las tareas en el experimento informático, la verificación de respuestas y la presentación de los resultados de resolviendo tareas en papel junto con el Blank. Las tareas experimentales incluyen la implementación de los parámetros especificados en el modelo de ordenador, la definición de la obra, el calor y la eficiencia de un motor. Las tareas ambiguas requieren encontrar las temperaturas de un calentador y un refrigerador para alcanzar un coeficiente de funcionamiento dado. Las tareas de investigación incluyen una serie de cuestiones sobre el aumento del coeficiente de rendimiento de un motor. |
Computer laboratory work is conducted to reinforce the subject being studied, and its adequate organization and implementation has a large impact on activization, motivation and, ultimately, the effectiveness of training. The lack of teachers’ practical ability to use computer models of physical phenomena for the organization of laboratory work is increasingly becoming one of the difficult problems of introducing its results in educational institutions. The products of the "Physicon" company (CD of the “Physicon” company, 2001) helped us to develop the models of blank forms for carrying out computer laboratory works on studying various physical phenomena (Kabylbekov and Bayzhanova, 2011; Kabylbekov et al., 2013a; Kabylbekov et al., 2013b; Kabylbekov et al., 2014; Kabylbekov et al., 2015a-f; Kabylbekov, 2015; Kabylbekov et al., 2016a-d).
This paper elaborates and presents the model of a blank form for the organization of computer laboratory work on studying the engine making a Carnot cycle, including short theoretical data, introductory assignments with the computer model, tasks with the subsequent computer checkout of answers, ambiguous tasks as well as experimental, research and creative tasks. They could be of practical use for teachers of schools, colleges and students-future teachers of the discipline "Physics" in everyday practice.
The model of a blank form includes the following materials:
Thermal engines are devices in which heat is converted into work. The working substance in any thermal engine is successively brought into thermal contact with hot bodies (heaters), obtaining from them some heat Q1, and with cold bodies (coolers), giving them the amount of heat Q2<Q1, and periodically returns to the original state. Such processes are called cyclic or circular processes (De Corte, 2014).
Thermodynamics asserts that it is impossible to convert all the heat Q1, obtained in the circular process from heaters, into work (the second law of thermodynamics). According to the law of energy conservation (the first law of thermodynamics), the work done by an engine is:
The coefficient of performance of a thermal engine is the ratio:
A Carnot cycle is an idealized circular process in which the working substance (ideal gas) is periodically brought into thermal contact with only one heater and one cooler. A Carnot cycle consists of two isotherms and two adiabats (Figure 1).

Figure 1. The structure of a Carnot cycle
Isothermal expansion at temperature T1 (AB): (T1 = const; V2 > V1; p2 < p1.); p is the pressure; V is the volume. The supplied heat Q1 is equal to the work of expansion А12, made by the gas through the transition from state A to state B: (Q1 = A{12}.).
Adiabatic expansion Q = 0 (BC): (T2 < T1; V3 > V2; p3 < p2.); heat exchange with the environment is absent, and the work of expansion A23 is made by changing the internal energy: (A{23}={∆ U}).
Isothermal compression at temperature T2 (CD): (T2=const; V4 < V3; p4 > p3.); the amount of the heat Q2, given by the gas to the cooler under isothermal compression, is equal to the work of compression A34. (A{34}= -Q2.)
Adiabatic compression is Q = 0 (DA): (T1> T2; V1 <V4; p1> p4.); the work of adiabatic compression (A {41} = -A {23}.).
The reverse Carnot cycle during the operation of a cooler is performed in the following order.
Adiabatic compression. A compressor compresses the vapor of a refrigerant, increasing its temperature and pressure.
Isothermal compression. The high-temperature compressed vapor of a refrigerant dissipates heat to the environment (a high-temperature reservoir) when flowing through the radiator outside the cooler. The vapor of a refrigerant is condensed (compressed) into the liquid phase.
Adiabatic expansion. The liquid refrigerant flows through the expansion valve to reduce its pressure.
Isothermal expansion. The cold liquid refrigerant evaporates when passing through the heat exchange tubes inside the cooler. In the process of evaporation, its internal energy grows, and this growth is provided by the selection of heat from the interior of the cooler (a low-temperature reservoir), as a result of which it cools. Then the gas enters the compressor for compression again. The reverse Carnot cycle is repeated (Petryakova, 2013; Blokhina, 2011).
The French engineer Carnot proved that the coefficient of performance of such an ideal thermal engine is maximum at these values and is equal to:

Any real thermal engine working with a heater of temperature T1 and a cooler of temperature T2 cannot have the coefficient of performance exceeding ηмах.
A Carnot cycle of an ideal thermal engine on the P, V - diagram goes in a clockwise manner. However, it can be carried out in the opposite direction (a cooling cycle). In this case, the system takes heat away from the cold body and transfers it to the hot body. For such a process to be possible, the positive work A should be performed on the system. A cooling cycle is implemented in cooling machines.
The significance of a Carnot cycle
A Carnot cycle played an important role in establishing the second law of thermodynamics: it helped to prove the equivalence of the formulas of R. Clausius and W. Thompson. A Carnot cycle was used to determine the absolute thermodynamic temperature scale, and was often applied for deriving various thermodynamic ratios (Sviridenko, 2011).
The interpretation of thermodynamic provisions often admits incorrect statements and conclusions (Kabylbekov et al., 2016e). In particular, the question of the thermal efficiency of inverse equilibrium processes and the place of a Carnot cycle in this group of circular processes has not yet been solved. One formulation of the second law of thermodynamics indicates the existence of a certain limit for thermal efficiency, the boundaries of which are determined by the most efficient direct Carnot cycle. Direct and reverse cycles consider the transformation of some types of energy into others, provided the conservation law is fulfilled. The account of non-equilibrium state gives an adjustment in the analysis of processes for real cycles. In terms of efficiency, one can formulate, as well as in terms of entropy, the efficiency and direction of energy conversion. Therefore, the consideration of direct and inverse cycles can be useful in both chemical and technical thermodynamics (Kormiltseva, 2011).
When comparing reversible cycles (we shall not discuss the reversibility condition here), a Carnot cycle (Kabylbekov et al., 2016f) is taken as the standard, which is considered to be the most profitable in the direct and inverted form. The superiority of the reverse Carnot cycle is postulated in terms of economic efficiency: cooling and heating coefficients (Kabylbekov et al., 2016f; 2017a; 2017b; Barkovskiy et al., 1999). In proving this, either erroneous assumptions are made, or the conditions of comparison are taken to be arbitrary (Kabylbekov et al., 2017a; 2017b). It is erroneous to assert (see, for example, (Kabylbekov et al., 2016e)) that the cooling coefficient of a Carnot cycle has the greatest value in comparison with other reverse cycles at given temperatures of heat sources. In particular, for inverse cycles, the following inequality is considered to be justified (Kabylbekov et al., 2017a):

However, the relationship between the cooling coefficient and the thermal coefficient of performance is such (Kabylbekov et al., 2016f) that the more efficient the direct cycle, the less effective it is in its reversed form.
The idea of the place of a Carnot cycle among other reverse cycles is difficult to be formed due to the lack of an indicator similar to the thermal coefficient of performance of direct cycles. Therefore, it is inexpressive (Bazarov, 1993) to explain the impossibility of spontaneous energy concentration by means of a heat pump in violation of the second law of thermodynamics.
It is impossible to formulate the second law of thermodynamics through the existing efficiency indicators of reverse cycles. The "mechanical" transfer of the statement about a Carnot cycle, as the most effective among direct ones to inverse ones, as shown in this paper, is erroneous. For the analysis, we will give the well-known theorems (Kavtrev, 2001).
The first theorem of Carnot.


Figure 2. Writing an arbitrary cycle into a Carnot cycle


The characteristics of ε and ψ are convenient for evaluating the useful qualities of the reverse cycle, but they do not reflect the manifestations of the second theorem, as can be done with the thermal coefficient of performance of the direct cycle. The absence of such an indicator - the thermal coefficient of performance of the reverse cycle - makes it difficult to obtain consistent results in thermodynamic analysis (Hertel et al., 2003).

The theorem on the additivity of the coefficient of performance of direct and reverse cycles

This statement can be considered as the theorem on the additivity of the coefficients of performanceof direct and reverse cycles, the analytic expression of which, along with (6) - (9), combines the indicators of both groups of circular processes (Kirillin et al., 1983). With an increase in the difference between the temperatures of hot and cold sources, an increase of ñ and a decrease of ñ occurs in every cycle. Formula (10) is a rational expression for the condition of the reversibility of heat transformations and the work in a circular process conducted in the direct and then in the opposite direction, or in the system of two identical conjugate cycles, one of which is direct and the other is inverse (Figure 2), and is equivalent to this condition in the form (6) - (8).
The theorem (10) shows that the derivation (Kabylbekov et al., 2013b) for the equality of the coefficients of performance of conjugate cycles seems to be erroneous (Figure 3).

Figure 3. The derivation (Kabylbekov et al., 2013b) for the equality
of the coefficients of performance of conjugate cycles
One can formulate the second law of thermodynamics from the point of view of the coefficient of performance of the reverse cycle: it is impossible to completely transfer energy from the cold body to the hot one without additional energy costs (energy compensation), i.e. ñ, set to unity, is unattainable (Krutova, 1981). Equilibrium conditions provide the greatest value of the coefficient of performance of direct and reverse cycles. We obtain some "inverse" principle of Carnot: the greater the temperature difference between the two sources, the lower the efficiency of machines and devices operating in the reverse cycle (Table 1).
Table 1. The coefficient of performance of thermal engines in %
Engine |
Coefficient of performance, % |
Steam engine |
1 |
Locomotive |
8 |
Carburetor engine |
20-30 |
Gas turbine |
36 |
Steam turbine |
35-46 |
Rocket engine with liquid fuel |
47 |
In assignments with the subsequent experimental verification of answers on the computer model, it is necessary to solve tasks on paper beforehand, to implement the given conditions on the computer model, and to compare the results with the indications of the computer model. The course of solving problems must be submitted together with the blank form. Experimental and research tasks provide for the realization of computer experiment conditions by the given parameters, the determination of the initial and final temperature and their difference, changes in the internal energy, work, the amount of the heat received from a heater and given to a cooler with the analysis of the experimental result and the formulation of the conclusion, the correspondence of the results to the first law of thermodynamics (Feng, 1986; Fradkin, 2002; Kavtrev, 2002; Gomulina, 2003; Leonov, 2001).
Tasks with missing data assume an independent selection of one or more of the missing elements. It is clear that there can be several answers when solving ambiguous tasks. Therefore, the solution of ambiguous problems involves the selection of two interrelated parameters that satisfy a given condition. Research and creative tasks include a number of questions related to the experimental determination of experimental parameters to achieve the required coefficient of performance of the thermal machine operating in the direct Carnot cycle and ways to implement them as well as to offer a proposal to increase this coefficient (Kvasnikov 1991; Orir, 1981; Bushuyev, 2011).
• Present a Carnot cycle in P, V and S, T-diagrams. (The latter is offered only for students, since the concept of entropy is not provided in the school curriculum). Answers: ...................
• Describe each of the processes involved in the direct Carnot cycle. Answers: .......................
• Write down the formula for the coefficient of performance of an ideal thermal engine operating in a Carnot cycle. Answers: .................................
• What values determine the operation of an ideal thermal engine in one cycle? Answers: ....
• How will the coefficient of performance of a Carnot cycle change, if the temperature of a heater raises two times? Answers: ........................
• Give the definition of the first and second theorem of Carnot. Answers: ...............................
• What is the relationship between the thermal coefficient of performance of an arbitrary direct cycle and the efficiency of reverse cycles? Answers: ...........................................
• What is the sum of the thermal coefficients of performance for any circular process? Answers: ………………
• What is the additivity of the thermal coefficients of performance of direct and reverse cycles? Answers: .....................
• Is it possible to build an engine that will not receive energy from outside? Answers: ...........
• Is it possible to turn all the heat received by an engine into work? Answers: .............
• Which body spontaneously transmits heat? Answers: ...................
• How can heat be transferred from the cold body to the hot one? Answers: .............
• How can the efficiency of a thermal engine be increased? Answers:…….
• Is it possible to lower the room temperature by opening the door of a working fridge? Answers:……
• Is it possible to achieve a 100% efficiency by reducing friction to zero between all parts of the machine? Give an explanation. Answers: .............
• Does the efficiency of an ideal engine that performs a Carnot cycle depend on the nature of the working substance? Answers: .........................
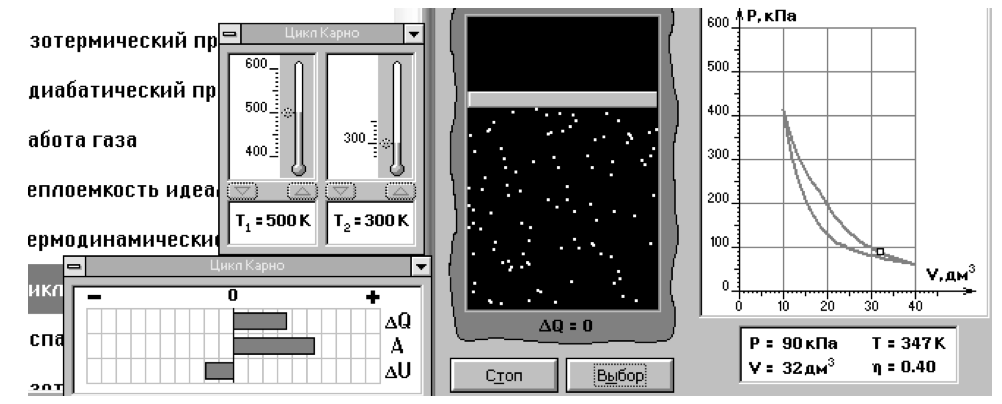
Figure 4. Still frame of a Carnot cycle (437)
1. Introductory tasks with the computer model.
1.1. Within what limits can the temperature of a heater (cooler) be changed (Figure 4)? Answers: ...............
1.2. What is the amount of the ideal gas in the chamber? Answers: ................
1.3. Within what limits does pressure (and the volume of the working substance) change at the temperature of a heater of 600K and the temperature of a cooler of 270K for one complete cycle? Answers: .............................
1.4. Set the temperature of a cooler Т2 =300К, and the temperature Т1=600К. Begin the process at the highest and lowest temperatures and describe the processes that take place sequentially in the direct direction for one complete cycle. Answers: ..........
1.5. Draw the direct and reverse Carnot cycles in the S, T-diagram. Answers: .....................
1.6. How can the work of the direct Carnot cycle be determined through the S.T diagram? Answers:…….
2. Tasks with subsequent computer verification
2.1. Determine the coefficient of performance of an ideal thermal engine at the temperature of a heater of 600K and the temperature of a cooler of 350K (300K, 270K). Answers: ............
3. Experimental tasks
3.1. Set the temperature of a heater Т1=600К (500K), the temperature of a cooler Т2=350К and determine the volume of the working substance according to the model’s indicators. What is the amount of the substance? Answers: .............
3.2. At the temperature of a heater Т1=450К (600K), the working substance receives heat from a heater Q1=500 J and gives heat to a cooler Q2=350 J (500 J). What kind of work is performed in one cycle and what is the coefficient of performance? What is the change in the internal energy of the working substance? Answers: .............
3.3. The parameters of the working substance at the beginning of a cycle are P1=416kPa, Т1=500К, V1=10 дм3. Determine the amount of substance used in the model. Answers: …….
4. Ambiguous tasks.
4.1. Determine the temperature of a heater and a cooler of the thermal engine operating in a Carnot cycle with the coefficient of performance of 50% (40%, 20%). Answers: ...................
4.2. At what temperature difference between a heater and a cooler can the maximum coefficient of performance be reached for the given computer model? Answers: ............
4.3. Determine the amount of heat received from a heater and given to a cooler of the thermal engine making a Carnot cycle with the coefficient of performance of 50%. Answers:..
5. Research assignments.
5.1. The temperature of a cooler is Т2=270К. What should the temperature of a heater of the thermal engine operating in the direct Carnot cycle be under the coefficient of performance of 55%? Answers: ...........
5.2. A thermal machine making a Carnot cycle receives 500 J of heat per cycle from a heater at a temperature of Т1=450К (600K) and gives a cooler 350 J (300 J) of heat. Determine the temperature of a cooler T2 and the coefficient of performance of a thermal machine. Answers: ......
5.4. Use the experimental data to determine what ideal gas is embedded in the computer model. Answers: ............
5.5. Determine the maximum coefficient of performance which can be obtained through this computer model. Answers: ............
6. Creative tasks.
6.1. Suggest the initial parameters at which the coefficient of performance of 50% (55%) can be achieved. Answers: ......
6.2. Suggest how the coefficient of performance of thermal machines making a direct Carnot cycle can be increased. Proposal: ...................................
6.3. Independently make up several tasks taking into account the possibility of the computer model. Answers: ......
Table 2. Count of students’ answers
Number of completed tasks |
Number of mistakes |
Assessment |
|
|
|
The proposed model of the blank form for the organization of computer laboratory work on studying the engine that performs a Carnot cycle includes brief theoretical data, introductory tasks with the computer model, tasks with the subsequent computer checkout of answers, ambiguous tasks, experimental, research and creative tasks.
Brief theoretical data gives the definition of a thermal engine, describes the principle of an engine’s operation, the processes of a Carnot cycle, the efficiency of a thermal engine, the operation of a cooling machine and some confusing questions on explaining the coefficients and efficiencies of direct and reverse Carnot cycles.
Introductory tasks with the computer model include a variety of questions related to the ability to change the parameters (pressure and temperature) of processes, to determine the volume of the working substance, taking into account the possibility of the model. Experimental tasks include the implementation of the specified parameters on the computer model, the definition of the work, heat and efficiency of an engine. Ambiguous tasks require finding the temperature of a heater and a cooler for achieving a given coefficient of performance. Research tasks include a number of issues on increasing the coefficient of performance of an engine.
Barkovskiy, Yu. B., Moos, E. N., Tabunov, N. I. (1999). The efficiency of reverse cycles. Journal of Technical Physics, 69(6), 618-620.
Bazarov, I. P. (1993). Delusions and errors in thermodynamics. Moscow: MGU, 56 p.
Blokhina, S. N. (2011). Development of a physics lesson in 8th grade "Refraction of light". Issues of Education, 98, 41-59.
Bushuyev, L. G. (2011). Formation of information competence in physics lessons. Issues of Education, 88, 11-22.
CD of the “Physicon” company. "Open Physics 1.1". (2001).
De Corte, E. (2014). Innovative perspectives of studying and teaching in the field of higher education in the 21st century (Translated from English by E. Shadrina). Issues of Education, 3, 8-29.
Feng, J. (1986). Machines, energy and entropy. Trans. from English. Moscow: Mir, 336 p.
Fradkin, V. E. (2002). Teachers’ mastering the ways of implementing the educational potential of new information technologies in the process of professional development. Abstract of Doctoral Dissertation, St. Petersburg, 25 p.
Gomulina, N. N. (2003). Technique of carrying out computer laboratory work using the multimedia course "Open Physics 2.5". Interaction of parallel currents. http://www.college.ru/physics/op25part2/planning/teach/lessons.html
Hertel, G., Senichenkov, Yu. Bю, Novik, L. V. (2003). "Sir Newton, what do you think about computer training?" - Journal "Computer Tools in Education". St. Petersburg: Informatization of Education, 1, 60-66.
Kabylbekov, K. A., Bayzhanova, A. (2011). The use of multimedia capabilities of computer systems to expand the demonstration resources of some physical phenomena. Proceedings of the All-Russian Scientific and Practical Conference. Conference with international participation, Tomsk, 210-215.
Kabylbekov, K. A., Saydakhmetov, P. A., Arysbayeva, A. S. (2013a). The model of the blank for the organization of students’ independent performance of computer laboratory works. Proceedings of the National Academy of Sciences of the Republic of Kazakhstan, Series of Physics and Mathematics, 6, Almaty, 82-89.
Kabylbekov, K. A., Saydakhmetov, P. A., Baydullayeva, L. E., Abduraymov, R. (2013b). Methods of application of the regularities of photo and Compton effects, models of blank forms for the organization of computer laboratory work. Proceedings of the National Academy of Sciences of the Republic of Kazakhstan, Series of Physics and Mathematics, 6, Almaty, 114-121.
Kabylbekov, K. A., Saydakhmetov, P. A., Turganova, T. K., Nurullayev, M. A., Baydullayeva, L. E. (2014). The lesson model on the collecting and scattering lens. Proceedings of the National Academy of Sciences of the Republic of Kazakhstan, Series of Physics and Mathematics, 2, Almaty, 286-294.
Kabylbekov, K. A. (2015). Organization of computer laboratory work. Textbook. Shymkent, 77 p.
Kabylbekov, K. A., Ashirbayev, Kh. A., Saydakhmetov, P. A., Rustemova, K. Zh., Baydullayeva, L. Ye. (2015a). The blank model for the organization of the performance of computer laboratory work on the investigation of light diffraction. Proceedings of the National Academy of Sciences of the Republic of Kazakhstan, Series of Physics and Mathematics, 1(299), Almaty, 71-77.
Kabylbekov, K. A., Ashirbayev, Kh. A., Takibayeva, G. A., Saparbayeva, E. M., Baydullayeva, L. E., Adineyeva, Sh. I. (2015b). The blank model for the organization of computer laboratory work on the motion of charged particles in the magnetic field and the operation of a mass spectrometer. Proceedings of the National Academy of Sciences of the Republic of Kazakhstan, Series of Physics and Mathematics, 1(299), Almaty, 80-87.
Kabylbekov, K. A., Ashirbayev, Kh. A., Saydakhmetov, P. A., Baygulova, Z. A., Baydullayeva, L. E. (2015c). The blank model for the organization of computer laboratory work on the study of Newton's rings. Proceedings of the National Academy of Sciences of the Republic of Kazakhstan, Series of Physics and Mathematics, 1(299), Almaty, 14-20.
Kabylbekov, K. A., Ashirbayev, Kh. A., Sabalakhova, A. P., Dzhumagaliyeva, A. I. (2015d). The blank model for the organization of the performance of computer laboratory work on the study of light interference. Proceedings of the National Academy of Sciences of the Republic of Kazakhstan, Series of Physics and Mathematics, 3(301), Almaty, 131-136.
Kabylbekov, K. A., Ashirbayev, Kh. A., Sabalakhova, A. P., Dzhumagaliyeva, A. I. (2015e). The blank model for the organization of study on the effects of the Doppler computer model. Proceedings of the National Academy of Sciences of the Republic of Kazakhstan, Series of Physics and Mathematics, 3(301), Almaty, 155-160.
Kabylbekov, K. A., Ashirbayev, Kh. A., Arysbayeva, A. S., Dzhumagaliyeva, A. M. (2015f). The blank model for the organization of computer laboratory work on the study of physical phenomena. Moscow: Modern High Technologies, 4, 40-43.
Kabylbekov, K. A., Saydakhmetov, P. A., Ashirbayev, Kh. A., Omashova, G. Sh., Berdaliyeva, Zh. (2016a). The blank model for the organization of computer laboratory work on the study of electromagnetic oscillations. Proceedings of the National Academy of Sciences of the Republic of Kazakhstan, Series of Physics and Mathematics, 1(305), 111-116.
Kabylbekov K. A., Saidakhmetov P. A., Omashova G. Sh., Berdalieva Zh., Dzhumagalieva A. I. (2016b). The blank model for the organization of computer laboratory work on the study of the interaction of two infinitely long parallel conductors with currents. Proceedings of the National Academy of Sciences of the Republic of Kazakhstan, Series of Physics and Mathematics, 1(305), 135-140.
Kabylbekov, K. A., Saydakhmetov, A. A., Omashova, G. Sh., Suttibayeva, D. I., Kozybakova, G. N. (2016c). The blank model for the organization of computer laboratory work on the study of the isobar process. Proceedings of the National Academy of Sciences of the Republic of Kazakhstan, Series of Physics and Mathematics, 2, 92-97.
Kabylbekov, K. A., Saydakhmetov, P. A., Omashova, G. Sh., Abekova, Zh. A., Nurullayev, M. A. (2016d). The blank model for the organization of the performance of research assignments in physics. Proceedings of the National Academy of Sciences of the Republic of Kazakhstan, 3, 67-73.
Kabylbekov, K. A., Saydakhmetov, P. A., Ashirbayev, Kh. A., Abdubayeva, F. I., Doskanova, A. E. (2016e). The study of the work of gas on the computer model. Proceedings of the National Academy of Sciences of the Republic of Kazakhstan, 2, 83-88.
Kabylbekov, K. A., Saydakhmetov, P. A., Omashova, G. Sh., Serikbayeva, G. S., Suyerkulova, Zh. N. (2016f). The blank model for the organization of computer laboratory work on the study of free mechanical vibrations. Proceedings of the National Academy of Sciences of the Republic of Kazakhstan, Series of Physics and Mathematics, 2, 84-91.
Kabylbekov, K. A., Madiyarov, N. K., Saydakhmetov, P. A. (2016g). The independent construction of research tasks for computer laboratory work on thermodynamics, Proceedings of the IX International Scientific and Methodic Conference, Teaching of natural sciences (biology, physics, chemistry), mathematics and computer science, Tomsk, 93-99.
Kabylbekov, K. A., Saydakhmetov, P. A., Omashova, G. Sh. (2017a). Aynymaly current tizbegindegi inductive coil reaktivi kedergіsіnің current zhilіgіne tәuеldіgіn zertteuge arnalғan computer izerthanalyұ zhmyysty ұyymdastyru. Proceedings of the National Academy of Sciences of the Republic of Kazakhstan, 1, 77-82.
Kabylbekov, K. A., Saydakhmetov, P. A., Omashova, G. Sh., Ashirbayev, Kh. A., Abekova, Zh. A. (2017b). Organization of computer laboratory work on the study of real-gas isotherms. Proceedings of the National Academy of Sciences of the Republic of Kazakhstan, 1, 77-83.
Kavtrev, A. F. (2001). Laboratory work for the computer course "Open Physics". Uniform motion. Simulation of inelastic collisions. Newspaper "Physics", 20, 5-8.
Kavtrev, A. F. (2002). The experience of using computer models in physics lessons. Issues of Internet Education, 3.
Kirillin, V. A., Sychev, V. V., Sheindlin, A. E. (1983). Technical thermodynamics, 4th ed. Moscow: Energoatomizdat, 416 p.
Kormiltseva, L. A. (2011). Lesson-project "Atomic physics". Issues of Education, 97, 23-34.
Krutova, V. I. (1981). Technical thermodynamics. Textbook for high schools, 2nd ed. Moscow: Vysshaya Shkola, 493 p.
Kvasnikov, I. A. (1991). Thermodynamics and statistical physics. Theory of equilibrium systems. Moscow: MGU, 800 p.
Leonov, N. F. (2001). The use of computers for teaching physics. Issues of Internet Education, 2. http://archive.1september.ru/fiz/2001/20/no20_02.html
Nashchokin, V. V. (1980). Technical thermodynamics and heat transfer, 3rd ed. Moscow: Vysshaya Shkola, 469 p.
Orir, J. (1981). Physics. Trans. from English. Moscow: Mir, 336 p.
Petryakova, L. L. (2013). Efficiency coefficient. Summary of the physics lesson, 7th grade. Issues of Education, 114, 31-45.
Sviridenko, O. V. (2011). "Fundamentals of thermodynamics". Developing a physics lesson (10th grade) using electronic learning resource. Issues of Education, 88, 11-22.
Zhukovskiy, V. S. (1983). Thermodynamics. Moscow: Energoatomizdat, 304 p.
1. M.Auezov South Kazakhstan State University, Department of Theory and Methods of Teaching Physics, Kazakhstan
2. M.Auezov South Kazakhstan State University, Department of Physics for Technical Specialties, Kazakhstan
3. M.Auezov South Kazakhstan State University, Department of Theory and Methods of Teaching Physics, Kazakhstan
4. M.Auezov South Kazakhstan State University, Department of Physics for Technical Specialties, Kazakhstan
5. M.Auezov South Kazakhstan State University, Department of Theory and Methods of Teaching Physics, Kazakhstan
6. M.Auezov South Kazakhstan State University, Department of Water resources, Land Use and Agricultural Technology, Kazakhstan