

 Vol. 38 (Nº 45) Año 2017. Pág. 18
Vol. 38 (Nº 45) Año 2017. Pág. 18
Fernando Francisco PEREIRA 1; Maria Lucia de Carvalho FONTANINI 2; Armando Paulo da SILVA 3
Recibido: 28/05/2017 • Aprobado: 25/06/2017
RESUMO: Este artigo resulta de uma pesquisa qualitativa cujo objetivo foi analisar as compreensões dos futuros professores de um curso de licenciatura em Matemática acerca da Metodologia de Resolução de Problemas. Neste artigo se apresenta os resultados referentes as compreensões desses professores acerca das potencialidades e limitações do uso da Metodologia de Resolução de Problemas. Os dados foram coletados a partir de entrevistas semiestruturadas e analisados através da análise qualitativa livre, embasado em alguns pressupostos teóricos da análise textual discursiva. |
ABSTRACT: The article in question is results from a qualitative research that had as main objective to analyze the understanding of future teachers of a degree course in Mathematics about the Problem-Solving Methodology. In this article will be presented the results related the understanding of these future teachers about the potentials and limitations of using the Problem-Solving Methodology. The data were obtained from a semi-structured interview and analyzed through free qualitative analysis, based on some theoretical assumptions of discursive textual analysis. |
A educação tanto no contexto mundial como no brasileiro evoluiu com uma diversidade de pesquisas que são realizadas e aplicadas nas escolas visando contribuir com a formação dos professores e com novas metodologias que podem ser utilizadas, no intuito de tornar a sala de aula mais atrativa. Mas, a existência de novas metodologias de ensino não garante que os problemas que surgirem serão sanados em todas as escolas, e que, as pesquisas desenvolvidas serão propícias para aplicação em qualquer realidade de educação vivenciada, as metodologias, por si, não tem o potencial de garantir a aprendizagem dos alunos, é a ação do professor em sala de aula, a sua compreensão sobre a metodologia e do gerenciamento desta, em sala, que permite que uma determinada metodologia atinja os objetivos educacionais que se esperam ou não. Cyrino, Passerini (2009), Santos-Wagner, Nasser e Tinoco (1997) afirmam que, para muitos, o rendimento insatisfatório dos alunos em avaliações de aprendizagem escolar, está associado à má qualidade de ensino e ao despreparo dos professores para a prática letiva, assim segundo Garcia (2002) a formação de professores é definida como um fator decisivo na melhoria do ensino e, portanto, com grande influência no conhecimento social, jurídico, político e pedagógico de seu trabalho.
Em virtude do contexto apresentado, acredita-se que, a formação inicial de professores é uma etapa do processo de desenvolvimento profissional, o qual deve se estender ao longo de todo o período de atuação, além de que o conjunto de conhecimentos adquiridos durante essa etapa juntamente com os conhecimentos que esses futuros professores trazem de suas experiências quando estudantes, servirá de referência para sua prática em sala de aula. Assim, surge a necessidade de conhecer melhor as compreensões dos futuros professores que estão nas etapas finais de conclusão do Curso de Licenciatura em Matemática, acerca de uma metodologia em especifico, a Resolução de Problemas.
Procedente da pesquisa, neste artigo, será apresentado o referencial teórico, a metodologia utilizada na pesquisa, bem como a análise dos dados e os resultados obtidos acerca das potencialidades e limitações do uso da Metodologia de Resolução de Problemas em sala de aula, segundo a visão desses futuros professores.
A resolução de problemas, em sala de aula, pode ser vista como um recurso muito eficiente para promover o aprendizado dos alunos. Além do aprendizado dos conceitos matemáticos, a resolução de problemas é capaz de promover nos alunos aspectos atitudinais como cooperação, liderança, responsabilidade, entre outros.
Segundo Carlini (2004) apud Proença (2012) a resolução de problemas
(...) proporciona condições para realizar objetivos conceituais (organização relação e registro de informações diante de um problema concreto), [objetivos] procedimentais (busca de novas informações, formulação e testagem de hipóteses, elaboração de um plano de ação) e [Objetivos] atitudinais (responsabilidade, cooperação, autoconfiança). (Carlini, 2004 apud Proença, 2012)
Segundo Dante (2003), na Metodologia de Resolução de Problemas o professor aproxima-se dos alunos com uma proposta de trabalho que os desafia e torna as aulas de Matemática mais dinâmicas e motivadoras, fazendo o aluno sentir o prazer de aprender Matemática quando consegue resolver um problema por si próprio, mais do que o clássico esquema de explicar, repetir e fixar o conteúdo. A Metodologia de Resolução de Problemas espera desenvolver nos alunos a capacidade de se tornarem críticos e autônomos, capazes de desenvolver métodos e estratégias para resolver os problemas e de serem sujeitos ativos em sua formação
Mais do que nunca precisamos de pessoas ativas e participantes, que deverão tomar decisões rápidas e, tanto quanto possível, precisas. Assim, é necessário formar cidadãos matematicamente alfabetizados, que saibam como resolver, de modo inteligente, seus problemas de comércio, economia, administração, engenharia, medicina, previsão do tempo e outros da vida diária. E, para isso, é preciso que a criança tenha (...) a resolução de problemas como parte substancial, para que desenvolva desde cedo sua capacidade de enfrentar situações-problema. (Dante, 2003, p. 15).
A resolução de problemas como proposta metodológica tem por objetivo promover nos alunos diversas capacidades quando eles estão diante de situações problemas, essas capacidades seriam elaborar estratégias, desenvolver planos, a fim de enfrentar tais situações, despertando a prática da interpretação e o espírito de exploração, a capacidade de raciocinar, experimentar e validar soluções. Essa proposta também tem como foco promover a construção do conhecimento matemático de forma dinâmica envolvendo os alunos. Nesse processo, são abandonadas as formas de aprendizagem maçantes, ou seja, aquelas que desenvolvem apenas o hábito de reproduzir o conteúdo e aplicar fórmulas generalizadas. Essa forma de trabalhar pode contribuir para que o aluno encontre satisfação em estudar Matemática.
De acordo com as ideias de Boavida (1993)
Ensinar Matemática via resolução de problemas [cria] na sala de aula, dá um clima de suporte que [encoraja] a participação voluntária dos alunos, [estimula] sua curiosidade. Ensinar Matemática via resolução de problemas [cria] condições para que haja um justo equilíbrio entre o trabalho individual, o trabalho em pequeno grupo e o trabalho com toda a turma. (Boavida, 1993, p. 145-146).
Soares e Pinto (2001), tratando da Metodologia de Resolução de Problemas afirmam que
Quando se ensina através da resolução de problemas, ajuda-se os alunos a desenvolver sua capacidade de aprender a aprender, habituando-os a determinar por si próprios respostas às questões que os inquietam, sejam elas questões escolares ou da vida cotidiana, ao invés de esperar uma resposta já pronta dada pelo professor ou pelo livro-texto. (Soares e Pinto, 2001, p.1).
Segundo Onuchic e Allevato (2005) uma das vantagens de se usar a resolução de problemas em sala de aula é a ligação entre os conteúdos presentes nos currículos de Matemática. O problema é o ponto de partida e orientação para a aprendizagem e os professores através e durante a resolução dos problemas, devem fazer conexões entre diferentes ramos da Matemática, gerando novos conceitos e novos conteúdos.
Ainda de acordo com Onuchic e Allevato (2011)
[..] a resolução de problemas desenvolve o poder matemático nos alunos, ou seja, a capacidade de pensar matematicamente, utilizar diferentes e convenientes estratégias, permitindo aumentar a compreensão dos conteúdos e conceitos matemáticos, (...) desenvolve a crença de que os alunos são capazes de fazer Matemática e de que a Matemática faz sentido. [Ainda] a construção de conhecimentos, relacionados a conceitos e conteúdos matemáticos, se realiza de forma mais significativa e efetiva pelos alunos. (Onuchic e Allevato, 2011, p. 82)
Além de todas as contribuições que puderam advir do uso desta metodologia é preciso que o professor esteja também ciente das dificuldades e limitações que poderá vir a encontrar ao trabalhá-las em sala de aula.
O quadro 1 apresenta uma síntese dos resultados obtidos em uma pesquisa desenvolvida por Reis e Zuffi (2007) com relação as dificuldades e desdobramentos ao se trabalhar com a Metodologia de Resolução de Problemas, em uma escola pública de Ensino Médio, do estado de São Paulo.
Situações |
Dificuldade |
Desdobramento |
Sala Numerosa |
Não era possível dar atenção total a todos os grupos. |
Os alunos se habituaram e desenvolveram tentativas de resolver os problemas sozinhos. |
Alunos inexperientes com a resolução de problemas |
Resistência e reclamação. |
Contato frequente com a resolução de problema amenizou a situação. |
Defasagem de conhecimento |
Lacuna na formação aritmética e algébrica, dificultou os cálculos na resolução dos problemas. |
Incentivou a estudarem mais, proporcionando-lhes momentos para exercitarem suas habilidades metacognitivas. |
Quadro 1 Resultados obtidos da pesquisa - situações enfrentadas, dificuldades e desdobramentos.
Fonte Adaptado de Reis e Zuffi (2007, p.134-135).
Outro fator que limita o uso da resolução de problemas consiste na carga horária dos professores. Professor com carga horária cheia representa um cenário negativo para implantação da resolução de problemas, uma vez que, para tal, o docente necessita se preparar. Tal preparação pressupõe estudo de temas relevantes, leitura de artigos de Educação Matemática, reunião com outros professores para propor trabalhos interdisciplinares em equipes, elaboração de problemas significativos para os alunos, etc. (Rodrigues e Magalhaes, 2011).
Ainda sobre os professores, Beatriz D’Ambrósio (2008) afirma que
É comum o professor “estragar” o problema, eliminando todo o desafio para o aluno. O problema resolvido pelo professor não tem o mesmo efeito daquele resolvido pelos alunos, sem muita intervenção do professor. Professores que alteram a demanda cognitiva de um problema não o fazem por mal, mas em geral o fazem para evitar o desânimo do aluno. [Os professores devem] confiar nas atividades dos alunos, [a desconfiança] no processo de construção do conhecimento, inevitavelmente resulta na eliminação (ou diminuição) das oportunidades oferecidas aos alunos para resolverem problemas. (D’ambrosio, 2008, p. 6).
Ainda, se tratando das limitações relacionadas aos professores e a Metodologia de Resolução de Problemas, Redling (2011) afirma
(...) os professores quando questionados a respeito das dificuldades em se trabalhar com problemas, relataram que a falta de tempo e o compromisso de cumprir ou seguir o cronograma, limita a utilização da resolução de problemas. (Redling, 2011, p. 123)
Borba e Penteado (2001) apud Romanatto (2012) afirmam que, em geral, professores optam por trabalhar no que eles chamam de zona de conforto, na qual quase tudo é previsível, conhecido e, por decorrência, controlável nas aulas. Para os autores, na resolução de problemas, os professores entram, quase sempre, no que eles denominam zona de risco, na qual impera a imprevisibilidade e a incerteza e por isso gera a necessidade constante de avaliação das consequências das ações propostas.
Afim de analisar qualitativamente as compreensões dos futuros professores acerca das potencialidades e limitações do uso da metodologia de resolução de problemas em sala de aula, é que se optou por coletar os dados por meio de uma entrevista semiestruturada, cujo roteiro fora pré-estabelecidos anteriormente, segundo Bogdan e Biklen (1994) esta forma de entrevista tem como objetivo registrar as descrições, conversas e diálogos, bem como seus apontamentos por escrito com o intuito de preservar os dados a serem analisados. Quanto aos sujeitos, optou-se por trabalhar com alunos que estavam cursando as disciplinas de Estágio Supervisionado B, C e D, do Curso de Licenciatura em Matemática, da Universidade Tecnológica Federal do Paraná, Câmpus Cornélio Procópio, o motivo se deu por considerar que ao cursar essas disciplinas, os alunos já tiveram contato com várias disciplinas da área de Educação Matemática, nas quais fizeram reflexões a respeito da resolução de problemas e é de se esperar que possuam alguns conhecimentos sobre essa metodologia. Ao chegar aos estágios de regências o aluno deve preparar as aulas que ministrará, o que envolve um estudo não só do conteúdo matemático, mas a decisão sobre qual metodologia ele utilizará para abordar este conteúdo. Os conhecimentos que ele traz das disciplinas anteriores, projetos em que participou, observação dos trabalhos de outros professores em sala de aula, poderão, então, subsidiar esta escolha e a experiência vivida no estágio. No total, 15 alunos aceitaram ser entrevistados, passando a serem identificados por meio de uma codificação de acordo com o estágio ao qual estava matriculado (B, C ou D) acrescido do número representando sua posição de entrevistado.
Por meio de uma investigação qualitativa livre (Bogdan; Biklen,1994), construiu-se um processo de análise dos dados que utilizou alguns elementos da Análise Textual Discursiva segundo Moraes e Galiazzi (2016).
Após a transcrição e leitura das entrevistas gerou-se um quadro com o intuito de agrupar as respostas dos entrevistados referentes a uma mesma pergunta. Neste processo foram percebidos alguns pontos em comum entre algumas respostas. Procurou-se reordenar o quadro, colocando-se próximas as respostas que possuíssem alguma similaridade a fim de destacar informações importantes, para criar as unidades de análise.
A criação das categorias e subcategorias se deu a priori, levando-se em consideração os objetivos da pesquisa. A categoria resolução de problemas foi escolhida em função do objetivo geral. E as subcategorias forma pensadas considerando os objetivos específicos da pesquisa.
A categoria escolhida foi: resolução de problemas. As subcategorias são mais especificas e elas se referem a quais aspectos sobre resolução de problemas são investigados. A saber: as potencialidades e limitações do uso da Metodologia de Resolução de Problemas em sala de aula.
Criando-se as categorias e subcategorias tendo em consideração os objetivos da pesquisa atende-se o critério de validade, colocado por Moraes e Galiazzi (2016). Segundo estes autores as categorias têm validade se elas são uteis a pesquisa. Ressalta-se também que as subcategorias têm validade teórica” pois elas se referem a aspectos ligados a metodologia de resolução de problemas, que são abordados em diversas pesquisas. Outra característica das categorias segundo os autores, é a homogeneidade, ou seja, a sua organização deve se dar a partir de um único critério. Isso ocorre, pois, cada subcategoria se refere a apenas um aspecto da resolução de problemas: as potencialidades e limitações do uso da Metodologia de Resolução de Problemas em sala de aula.
Neste trabalho as categorias também atendem ao aspecto da exaustão. Segundo Moraes e Galiazzi (2016), o fato da categoria ser exaustiva, não tem a ver com se utilizar todo o material coletado, mas sim implica que as informações tenham sido classificadas em função do objetivo da pesquisa. O que ocorre, pois buscou-se nos materiais coletados selecionar justamente os trechos que iam ao encontro dos objetivos da pesquisa.
Não se pretendeu neste trabalho que as categorias fossem excludentes, pois entendem-se que um mesmo sujeito devido a várias leituras feitas e diferentes experiências, pode enxergar diferentes potencialidades e limitações para utilizar a metodologia em sala de aula.
No Quadro 1 apresenta-se a estrutura de análise da pesquisa.
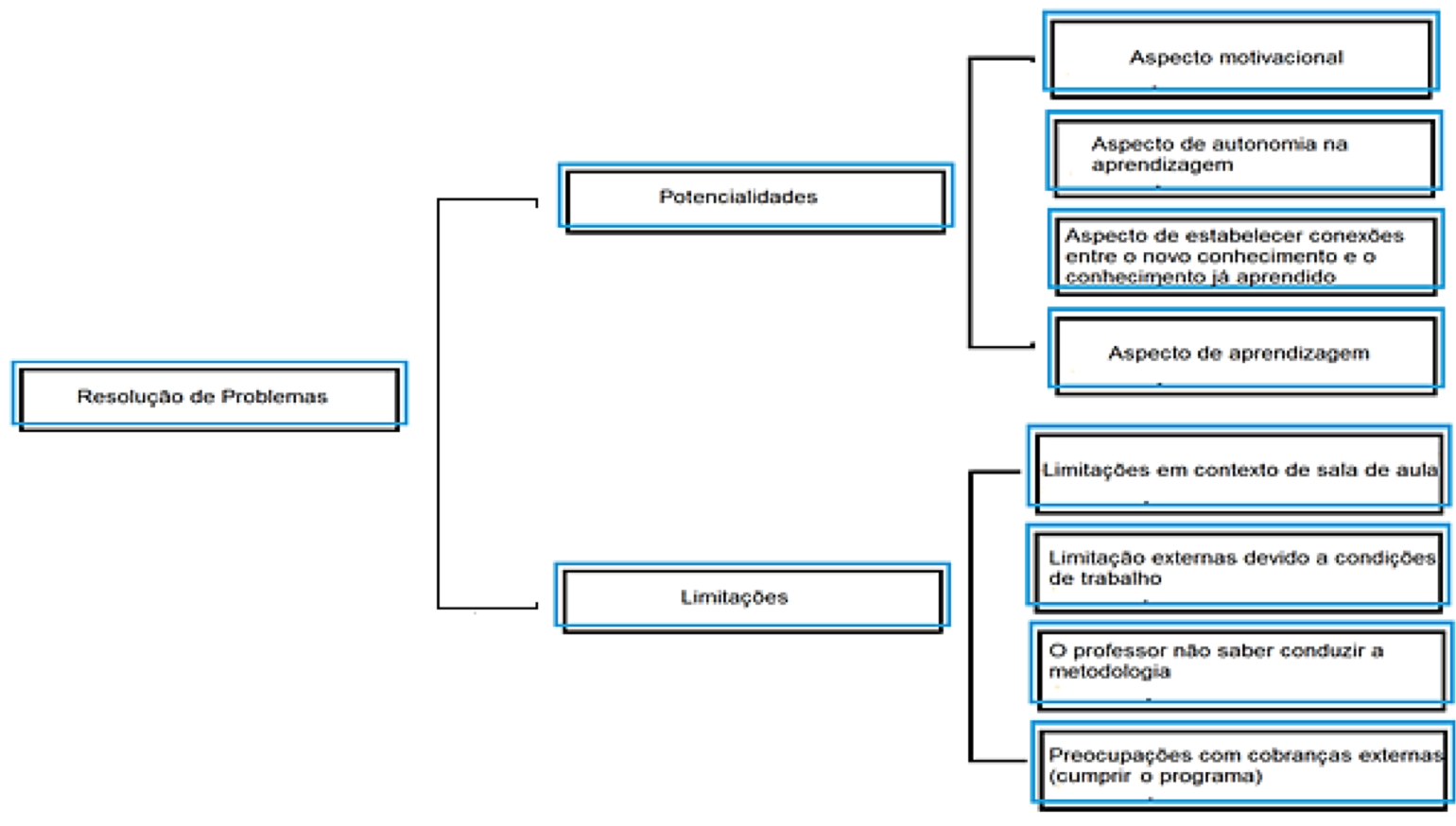
Figura 1 - Categoria, subcategorias e unidades de análise
Fonte: Dados da pesquisa
Após a definição da estrutura iniciou-se o processo de análise das transcrições afim de identificar a compreensão dos futuros professores acerca das potencialidades e limitações.
Os quadros apresentados referem-se a cada subcategoria. Em cada quadro são explicitados os critérios da classificação de cada subcategoria e de suas subunidades de análise. São também apresentados trechos dos referencias teóricos utilizados para definir cada unidade de análise. Cada unidade recebe um nome, que sintetiza as suas características. Nos quadros são também apresentados os trechos classificados em cada uma das unidades de análise, acompanhados do código do entrevistado.
Após cada quadro é apresentada uma tabela em que se procura indicar que percentagem dos participantes da pesquisa mencionou em suas respostas, aspectos que podem ser identificados em cada uma das unidades de análise. Com estas tabelas pretendia-se visualizar melhor, se haviam aspectos quanto a resolução de problemas, que eram percebidos pela maioria dos alunos e também aqueles que eram menos destacados.
Após a apresentação de cada tabela há um pequeno texto apresentado a análise do autor sobre as informações presentes no quadro e na tabela.
As informações contidas no quadro 2 referem-se ao perfil dos entrevistados. Essas informações além de serem uteis na análise, foram utilizadas para, compor o código utilizado na identificação dos entrevistados, durante a pesquisa.
Faz-se necessário uma sucinta explicação quanto à codificação de cada entrevistado. A letra “A” no início de cada código refere-se ao “aluno”, na sequência, o algarismo refere-se à ordem de entrevista, a letra “E” faz referência à palavra “estágio” e, por fim, cada letra ao final da codificação refere-se a um dos três estágios (B, C e D). A título de exemplo, o código A1EB refere-se ao “primeiro aluno da disciplina de Estágio B” submetido a entrevista.

Quadro 2 - Perfil dos alunos entrevistados.
Fonte: Dados da pesquisa
Na subcategoria Potencialidades, emergiu que, os vários participantes desta pesquisa e futuros professores não tem clareza quando se trata da utilização da Metodologia de Resolução de Problemas (para que serve), bem como dos passos que devem ser utilizados para aplicá-la em sala de aula.
A primeira análise apresentada no quadro 3 refere-se à subcategoria Potencialidades para se trabalhar em sala de aula com a Metodologia de Resolução de Problemas.
Subcategoria: Potencialidades Descrição: Nesta subcategoria procurou-se constatar quais as potencialidades de se trabalhar a Metodologia de Resolução de Problemas em sala de aula. Para isso, fez-se a seguinte pergunta aos entrevistados: quais são os pontos fortes de se usar essa metodologia em contexto de sala de aula? Procurou-se confrontar a visão dos entrevistados com as unidades de análise construídas a partir do referencial teórico. As ideias utilizadas para a análise desta unidade foram dos seguintes autores: Dante (2003), Boavida (1993) / Soares e Pinto (2001), Onuchic e Allevato (2005), Onuchic e Allevato (2011).
|
|
Unidades de Análise |
Respostas dos Entrevistados |
Aspecto motivacional |
“É ser algo que instiga os alunos a quererem descobrir a solução do problema (...)” A3EC “Acho que tornar a aula mais interessante, sei lá, e o conhecimento ser mais válido (...) A2EC “(...) seja uma maior interação do aluno, (...) ele sai do papel passivo para ativo, diferente de dar um exercício de resolva simplesmente, então o aluno tem que pensar e encontrar a saída, a solução para aquele problema (...)” A1ED (TEB) “(...) instigar o aluno a querer chegar a resposta (...)” A4ED (PEI) |
Aspecto de autonomia na aprendizagem |
“Acho que ajuda o aluno andar sozinho, descobrir sozinho o que tem que fazer, que fórmula ou conhecimento ele irá usar, por exemplo” A1EB (TEB/PEI) “Na Resolução de Problemas o aluno tem que aprender a caminhar usando seus próprios pés, por conta própria construindo o conhecimento (...)” A3EB (TEB/PEI) “Fazer o aluno ser um ser pensante, com seu próprio conhecimento e inteligência de buscar algum conceito já aprendido, assim, sem ajuda conseguir resolver o problema. ” A5EC (TEB/PEI) “(...) instigar o aluno a querer chegar à resposta. (...) o problema faz com que o aluno busque, lá no fundo, um conhecimento que ele já tem para traçar os objetivos e estratégias para que ele possa chegar à resposta (...)” A4ED (PEI) “(...) tentar aproxima o conteúdo e o aluno. E a Resolução de Problemas faz essa aproximação do conteúdo com o cotidiano do aluno. Então, assim, se aproximar do cotidiano dos alunos, faz com eles enxerguem a aplicação da Matemática e a interação (...)” A2ED (PEI) |
Aspecto de estabelecer conexões entre o novo conhecimento e o conhecimento já aprendido |
“(...) quando você trabalha com a Resolução de Problemas, não é só um conteúdo específico, aborda muito mais conteúdo que a criança precisa saber. Há uma diversidade de conteúdo que se pode trabalhar, por meio dessa metodologia (...)” A2EB (TEB) “(...) a metodologia de problemas pode resgatar outros conteúdos já aprendidos e outros conceitos que estão envolvidos naquele problema, não necessariamente algo específico, essa metodologia te dá um leque de opções de conceitos e conteúdo que se pode trabalhar. ” A6EC (TAB/PEI) “A resolução de problema não serve só para ensinar um tópico, e sim ensinar uma ampla quantidade de conteúdo. (...) faz com que o aluno busque lá no fundo, um conhecimento que ele já tem para traçar os objetivos e estratégias para que ele possa chegar à resposta (...)” A4ED (PEI) |
Aspecto de aprendizagem |
“(...) levar o aluno a raciocinar, levar o aluno chegar na resposta, sem dar a resposta a ele, mas fazer ele ter que pensar na resposta. Com certeza levar o aluno a entender e a resolver do jeito dele um problema de Matemática, no caso (...)” A1EC (PEI) “(...) não adianta levar o conteúdo todo mastigado ao aluno, a Resolução de Problemas faz com que o aluno pense, raciocine (...) o poder de contextualizar a Matemática e situações diárias e trabalhar o raciocínio dos alunos na busca por técnicas, e elaboração de estratégias para resolver o problema. ” A3ED (TEB/PEI) “Desde que seja de forma coerente. A resolução de exercício não seja encarado como uma resolução de problema. A resolução de problemas tem que ter um tipo de enredo, não que o aluno chegue a uma resposta, mas o caminho que ele fez, como ele chegou até aí, o que ele fez, o que ele usou (...)” A4EC (PEI) “(...) o aluno consegue aprender de uma certa maneira que ele não aprende no modo tradicional, (...) o aluno é capaz de realmente aprender o conteúdo e não decorá-lo (...)” A4EB (TEB) “(...) problematizar o conceito, faz com que os alunos não “ganhem” o conceito tão fácil, eles começaram a entender melhor como surge o conceito de determinada matéria. ” A5EB (TEB) |
Unidade: Aspecto motivacional – as respostas desta unidade baseiam-se nas ideias de Dante (2003), pois tornar a aula interessante e instigar o aluno a chegar a solução é deixar a aula dinâmica e motivadora. Ainda aparece, nas respostas dos entrevistados a ideia de deixar o aluno dar seus próprios passos, chegando à resposta por si só. Unidade: Aspecto de autonomia na aprendizagem – as respostas desta unidade estão de acordo com Boavida (1993) / Soares e Pinto (2001), haja visto que, nas respostas destaca-se a ideia do desenvolvimento da autonomia do aluno na busca pela resposta e soluções para o problema, sejam eles conhecimentos matemáticos ou de outras áreas e ligadas ao cotidiano. Unidade: Aspecto de estabelecer conexões entre o novo conhecimento e o conhecimento já aprendido – as respostas desta unidade estão de acordo com as ideias de Onuchic e Allevato (2005), onde são destacadas a necessidade de estabelecer conexões entre o novo conhecimento e os conhecimentos já aprendido. Unidade: Aspecto de aprendizagem – percebe-se nas respostas desta unidade uma aproximação às ideias de Onuchic e Allevato (2011), onde destaca-se o desenvolvimento do raciocínio e de estratégias e métodos para resolução dos problemas. Nota-se, ainda, a capacidade de compreender os conceitos matemáticos e como eles surgem, dando significado a eles. |
|
Quadro 3 – Potencialidades
Fonte: Dados da pesquisa
Na tabela 1 é apresentada a síntese dos resultados desta subcategoria com intuito de auxiliar a sua análise. Nesta tabela estão identificados os sujeitos de cada categoria de análise, bem como as frequências e as porcentagens.
Tabela 1 - Síntese dos resultados: Subcategoria Potencialidades
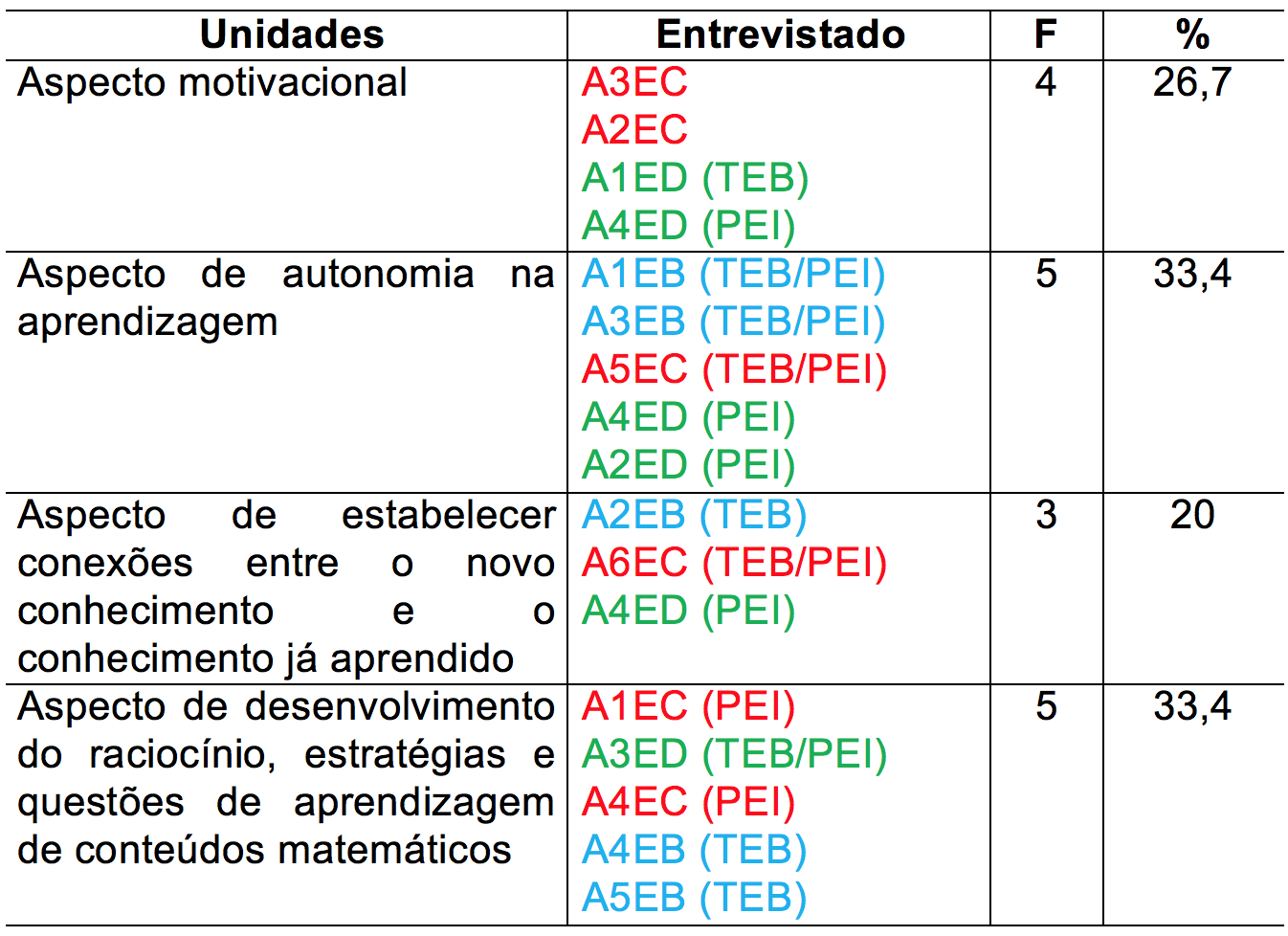
Fonte: Dados da pesquisa
Os resultados desta subcategoria apresentam que, conforme quadro 3 e tabela 1, todos os entrevistados tiveram suas falas em uma ou mais unidades de análise definidas, sendo que a fala do entrevistado A4ED está de acordo com 3 unidades de análise. Além disso, 33,4% dos entrevistados disseram que o potencial da Metodologia de Resolução de Problemas está ligado a aspectos de autonomia na aprendizagem e parte destes já haviam utilizado em algum momento do seu projeto de extensão e iniciação essa Metodologia.
Outro fato, é que as falas dos dois entrevistados que não tiveram experiência com a Educação Básica e/ou participaram de projetos de extensão e iniciação em relação às potencialidades desta metodologia, ficaram restritas ao aspecto motivacional.
No quadro 4, apresenta-se a subcategoria Limitações para se trabalhar em sala de aula com a Metodologia de Resolução de Problemas.
A partir da análise dessa subcategoria procurou-se as limitações de se trabalhar na sala de aula a Metodologia de Resolução de Problemas percebidas pelos futuros professores e para isso qual(is) o(s) ponto(s) fraco(s) de se trabalhar em sala de aula a Metodologia de Resolução de Problemas.
Subcategoria: Limitações Descrição: Nesta subcategoria procurou-se constatar quais as limitações de se trabalhar a Metodologia de Resolução de Problemas em sala de aula. Para isso, fez-se a seguinte pergunta aos entrevistados: quais são os pontos fracos de usar a Metodologia de Resolução de Problemas em contexto de sala de aula? Procurou-se confrontar a visão dos entrevistados com as unidades de análise construídas a partir do referencial teórico. As ideias utilizadas para a análise desta unidade foram as dos seguintes autores: Reis e Zuffi (2007), Rodrigues e Guimarães (2011), D’Ambrosio (2008), Redling (2011).
|
|
Unidades de Análise |
Respostas dos Entrevistados |
Limitações em contexto de sala de aula |
“Eu acho que é a falta de vontade dos alunos de pensar (...) não é comum os alunos terem contato com a resolução de problemas (...) algumas vezes os alunos podem não querer pensar e atrapalhar o professor.” A5EC (TEB/PEI) “Talvez a falta de um conceito ou de ideia do aluno para conseguir resolver o problema. Seria também as dificuldades que alguns alunos tem em alguns conteúdos.” A3EB (TEB/PEI) “(...)a maior dificuldade que eu sinto dos alunos, é a questão de interpretar o problema (...)” A2ED (PEI) “(...) sala numerosa, o que é a realidade da Educação Básica. A sala numerosa é uma dificuldade para o professor trabalhar com essa metodologia.” A4EB (TEB) É, eu acho que talvez na prática, na sala de aula, é o número de alunos (...)A1EC (PEI) |
Limitações externas devido a condições de trabalho |
“(...) não é fácil ter problemas para apresentar toda aula, e isso requer do professor que vai usar essa metodologia uma preparação, então o professor tem que primeiro ter resolvido o problema antes de apresentar para que ele saiba contornar qualquer situação que ocorra. O professor tem que se preparar para essa metodologia e ter um tempo disponível para preparar a aula, diferente de uma aula comum.” A1ED (TEB) “(...) a dificuldade de encontrar conteúdo ou elaborar um problema. Alguns temas são difíceis de trabalhar com a Resolução de Problemas e para achar problemas na internet ou em livros é difícil, (...) tem que pegar uns exercícios e dar uma modificada para se tornar Resolução de Problemas.” A2EB (TEB) |
O professor não saber conduzir a metodologia |
“(...) levar algo mastigado, pronto e simples de ser resolvido como um exercício. E o professor saber diferenciar problemas de exercícios, pois ele pode levar uma situação problema e acabar trabalhando como uma resolução de exercício.” A3ED (TEB/PEI) “O professor saber direcionar para o que ele exatamente quer, para ensinar determinado conteúdo. (...) o professor pode dar uma determinada situação e trabalhar de maneiras diferentes, (...) pode também não saber direcionar para o objetivo que ele quer, e eu acho que a dificuldade em ser o mediador, (...) tem que ter um jeito ou uma prática para poder conduzir do jeito que ele quer.” A2EC “(...) depende do professor (...) vai que o professor não sabe aplicar, aí ele acaba atrapalhando.” A3EC “(...) a maior dificuldade é criar esse tal problema para começar a matéria. Deve ser algo bem pensado para não virar somente um problema comum e simples que não servirá para introduzir nada, somente uma solução normal. A5EB (TEB) |
Preocupações com cobranças externas (cumprir com o programa) |
“Eu acho que perde muito tempo, por que o aluno fica lá pensando, as vezes à toa, pode ser que ele não consiga fazer de primeira então não vai ficar pensando e lendo de novo todo o texto.” A1EB (TEB/PEI) “Acredito também que falta de tempo, por que tem que dar aquele conteúdo e limitar à aquilo, talvez você tente levar algo novo mais você sempre vai pelo livro, mais é sempre assim.” A4EC (PEI) “A Resolução de Problemas não pode ser trabalhada com pouco tempo, pois é necessário que o aluno pense e reflita sobre o que ele está fazendo, e no final do semestre ou bimestre os professores tem que ter uma meta de conteúdo e, às vezes impede de utilizar esses mensagens de conteúdo e as vezes impede de utilizar essas metodologias.” A4ED (PEI) |
Unidade: Limitações em contexto de sala de aula – as respostas desta unidade estão de acordo com os relatos de Reis e Zuffi (2007). Pode-se identificar nas respostas do grupo a sala numerosa, a inexperiência dos alunos com a resolução de problemas e a defasagem de conhecimentos dos alunos em alguns conteúdos matemáticos. Unidade: Limitações externas devido a condições de trabalho – nas respostas desta unidade é possível ver a relação com as ideias de Rodrigues e Guimarães (2011). A falta de tempo do professor para se preparar é a principal limitação do uso da Resolução de Problemas segundo a resposta do grupo. Unidade: O professor não saber conduzir a metodologia - as respostas desta unidade identificam-se com as ideias de Beatriz D’Ambrosio (2008), quanto ao fato de o professor ter cautela quando conduzir uma resolução de problema e saber direcionar para o real objetivo. Unidade: Preocupações com cobranças externas (cumprir com o programa) - nota-se nas respostas dessa unidade, o tempo como fator negativo para se trabalhar com a Resolução de Problemas, haja visto que se deve cumprir um programa definido e limitar-se a trabalhar com a Metodologia de Resolução de Problemas demandaria tempo, assim como destacou Redling (2011). |
|
Quadro 4 – Limitações
Fonte: Dados da pesquisa
Na tabela 2 é apresentada a síntese dos resultados desta subcategoria com intuito de auxiliar a sua análise. Nesta tabela estão identificados os sujeitos de cada categoria de análise, bem como as frequências e as porcentagens.
Tabela 2 - Síntese dos resultados: Subcategoria Limitações
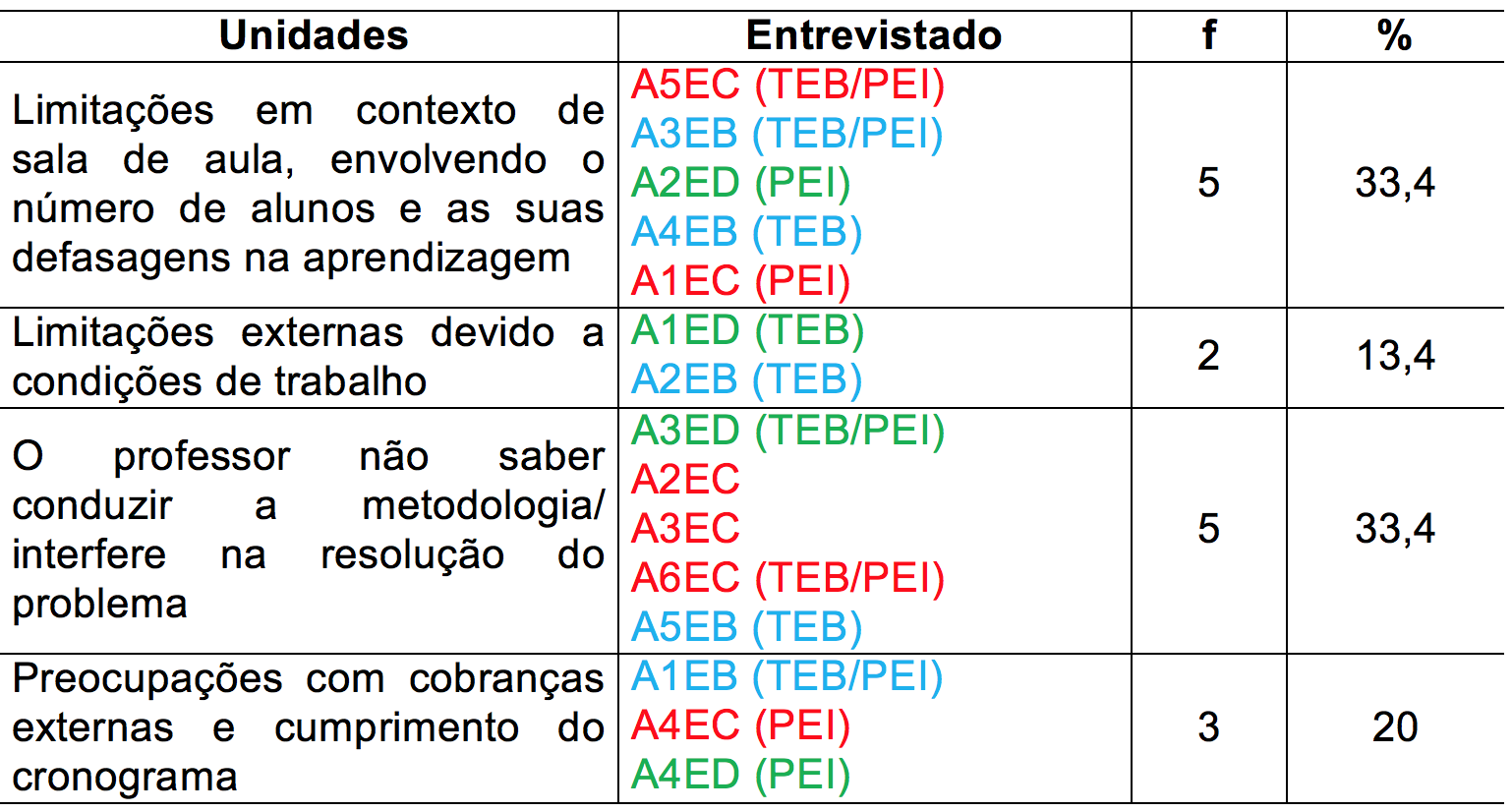
Fonte: Dados da pesquisa
Os resultados desta subcategoria apresentam que, conforme quadro 4 e tabela 2, todos os entrevistados tiveram suas falas classificadas em uma das unidades de análise definidas.
Percebe-se que parte dos entrevistados que trabalharam na Educação Básica atentam às limitações ligadas a problemas comuns enfrentados pelos professores, como salas numerosas, defasagem na aprendizagem e com ampla carga horária, com horas atividades não suficientes para se preparar para trabalhar com a Metodologia de Resolução de Problemas. Os entrevistados que não tiveram essa experiência somente consideram que a limitação desta metodologia está restrita ao fato do professor não saber conduzi-la, isso pode ser entendido que a falta de contato com a realidade vivenciada como professor possibilita que suas percepções estejam relacionadas somente a fatores ligados ao contexto de que ele não sabe direcionar ou aplicar essa metodologia.
Esta pesquisa teve como objetivo analisar as compreensões dos futuros professores acerca da Metodologia de Resolução de Problemas. Por meio de uma metodologia de análise livre, submeteu-se 15 alunos do Curso de Licenciatura em Matemática a uma entrevista buscando analisar quais as compreensões dos futuros professores acerca das potencialidades e limitações do uso desta metodologia em contexto de sala de aula.
Desta maneira conclui-se que o potencial da Metodologia de Resolução de Problemas, segundo a visão dos entrevistados vai ao encontro das ideias explicitadas no referencial teórico: a Metodologia de Resolução de Problemas, tornam as aulas de Matemática mais dinâmicas e motivadoras (Dante, 2003); contribuem para o desenvolvimento da autonomia do aluno, no processo de aprendizagem, levando-o a buscar suas próprias respostas (Boavida, 1993; Soares e Pinto, 2001); contribuem para o estabelecimento de conexões entre o conhecimento novo e o já aprendido (Onuchic e Allevato, 2005) e contribuem para a aprendizagem, aumentando a compreensão do conteúdo (Onuchic e Allevato, 2011). Quanto as limitações, esperava-se que os entrevistados vinculassem as limitações de se utilizar essa metodologia a contextos ligados aos conteúdos e processos matemáticos, porém verificou-se que grande parte dos entrevistados associam as limitações, à problemas peculiares aos enfrentados por professores da Educação Básica, como, sala numerosas, tempo hábil para preparação das aulas, entre outros.
Esta pesquisa, embora não envolvendo todos os alunos estagiários conseguiu traçar um retrato sobre as compreensões dos futuros professores, concluintes do Curso de Licenciatura em Matemática sobre a Metodologia de Resolução de Problemas bem como as potencialidades e limitações do seu uso em sala de aula.
Cyrino, M. C. C. T. (2006). Preparação e emancipação profissional na formação inicial de professores. En: Nacarato, A. M., y Paiva, M. A. V. P. (org.), A formação do professor que ensina Matemática, perspectiva e pesquisa (pp. 77-88). Belo Horizonte: Autêntica.
Bogdan, R. C., y Biklen, S. K. (1994). Investigação qualitativa em educação: uma introdução à teoria e aos métodos. Portugal: Porto.
Boavida, A. M. D. R. L. (1993). Resolução de problemas em educação Matemática: contributo para uma análise epistemológica e educativa das representações pessoais dos professores. (Tesis de Maestría). Universidade Nova de Lisboa - Faculdade de Ciências e Tecnologia. Lisboa.
D’Ambrósio, Beatriz. (2008). A evolução da resolução de problemas no currículo matemático. En: I Seminário de Resolução de problemas. Rio Claro. Recuperado de http://files.adrivargas.webnode.com.br/2000003427fdf080d90/linguagem_resolu%C3%A7%C3%A3o%20deproblemas.pdf.
Dante, L. R. (2003). Didática da resolução de problemas de Matemática. 1ª a 5ª séries. Para estudantes do curso de Magistério e professores do 1º grau. 12a ed. São Paulo: Ática.
Garcia, J. P. O. (2002). Breves notas para pensar à docência na perspectiva profissional. En: Cunha, E. R., y SÁ, P. F. de. (org.). Ensino e Formação docente: propostas, reflexões e práticas (pp. 17-25). Belém: A2 comunicações.
Moraes, R., y Galiazzi, M. do C. (2016). Análise textual discursiva. 3ª ed. rev. e ampl. Ijuí: Ed. Unijuí.
Onuchic, L. R., y Allevato, N. S. G. (2005). Novas reflexões sobre o ensino-aprendizagem de Matemática através da resolução de problemas. En: Bicudo, M. A. V., y Borba, M. C. (org.). Educação Matemática: pesquisa em movimento. (pp. 213-231).3 ed. São Paulo: Cortez.
(2011). Pesquisa em resolução de problemas: caminhos, avanços e novas perspectivas. Bolema, v. 25, n. 41, pp. 73-98.
Proença, M. C. de. (2012). A resolução de problemas na Licenciatura em Matemática: análise de um processo de formação no contexto do estágio curricular supervisionado. (Tesis de Doctorado). Universidade Estadual Paulista. Faculdade de Ciências. Bauru.
Santos-Wagner, V. M. P. dos., y Nasser, L., y Tinoco, L. (1997). Formação inicial de professores de Matemática. Zetetiké, v.5, n.7, pp. 37-49.
Soares, M. T. C., y Pinto, N. B. (2001). Metodologia da resolução de problemas. En: 24º Reunião Anual da ANPEd. Caxambu. Recuperado de http://24reuniao.anped.org.br/tp1.html.
Redling, J. P. (2011). A metodologia de Resolução de Problemas: concepções e práticas pedagógicas de professores de Matemática do Ensino Fundamental. (Tesis de Maestría) Universidade Estadual Paulista. Faculdade de Ciências, Bauru.
Reis, M. M. V., y Zuffi, E. M. (2007). Estudo de um Caso de Implantação da Metodologia de Resolução de Problemas no Ensino Médio. BOLEMA, Rio Claro, v. 20, n. 28, pp.113-138.
Rodrigues, A., y Magalhães, S. C. (2011). A Resolução de problemas nas aulas de Matemática: diagnosticando a prática pedagógica. FEOL, Oliveira, v.1, n.1.
Romanatto, M. C. (2012). Resolução de problemas nas aulas de Matemática. Reveduc, São Carlos, v. 6, n. 1, pp.299-311.
1. Universidade Tecnológica Federal do Paraná. Câmpus Cornélio Procópio – UTFPR – CP. Mestrando em Ensino de Matemática. Email: f.nando93@hotmail.com
2. Universidade Tecnológica Federal do Paraná. Câmpus Cornélio Procópio – UTFPR – CP. Mestre em Ensino de Ciências e Educação Matemática. Email: mariafontanini@utfpr.edu.br
3. Universidade Tecnológica Federal do Paraná. Câmpus Cornélio Procópio – UTFPR – CP. Doutor em Educação para a ciência. Email: armando@utfpr.edu.br