

 Vol. 38 (Nº 45) Año 2017. Pág. 1
Vol. 38 (Nº 45) Año 2017. Pág. 1
P. FREITAS-LEMES 1; D. VILELA 2; J.S.E. GERMANO 3; R. SANTOS 4; J. SAKURAGI 5
Recibido: 01/06/2017 • Aprobado: 15/06/2017
2. A tecnologia no ensino da geometria
RESUMO: Devido aos grandes avanços tecnológicos dos últimos anos o ensino tradicional tornou-se limitado e os próprios educandos exigem as alternativas digitais. Este trabalho tem como objetivo apresentar os resultados da intervenção pedagógica em 100 alunos do Ensino Fundamental, utilizando o software Wingeom como ferramenta de ensino da Geometria. O ganho educacional e o D de Cohen foram mensurados usando um pré e um pós-teste. O resultado indica que a |
ABSTRACT: This paper contribute to the pedagogical practice using Wingeom software as a teaching tool for Geometry. Due to the great technological advances of the last years the traditional education has become limited and the students themselves demand the digital alternatives. After conceptual classes on geometry with 100 students of the Elementary School, they explored the Wingeom tool in geometry classes. The educational gain was measured using a pre and post-test, as well as Cohen's statistical analysis. The results indicate that the Wingeom tool contributed positively to student’s improvement. |
A aprendizagem de geometria é uma importante ferramenta para a formação dos alunos. A resolução de problemas é umas das principais características da área de Ciências da Natureza, Matemática e suas Tecnologias e a utilização de ferramentas que auxiliem na resolução de tais problemas é fundamental para o entendimento do aluno nas diversas situações problemas que encontramos no ensino da matemática.
Ao educador cabe proporcionar meios para que o ensino seja significativo. A construção do conhecimento matemático deve ser contínua, a solução de pequenas dúvidas é um caminho para a verdadeira aprendizagem. De acordo com Paulo Freire (2002) ensinar não é transferir conhecimentos, mas criar as possibilidades para a sua própria produção ou a sua construção.
Os conceitos matemáticos não são compreendidos de modo desconexo. Ao longo do convívio com a matemática se criam condições de estabelecer uma lógica entre um assunto e outro. Cada área do ensino tem como objetivo auxiliar o aluno a compreender melhor o mundo em que ele está inserido, e auxiliá-lo futuramente em sua vida profissional.
Segundo o PCN (1999), ao se denominar uma área de estudo como sendo não só de Ciências e Matemática, mas também de suas tecnologias, sinaliza-se claramente que, em cada uma das suas disciplinas, pretende-se promover competências e habilidades que sirvam para o exercício de intervenções e julgamentos práticos.
A matemática é um importante meio de obtenção de conhecimento científico e de tecnologia que cada vez mais se expande, contribuindo assim na vida cotidiana do aluno para que ele compreenda e transforme sua realidade. Ensinar Matemática sem contextualizar o que se está explicando é construir no vazio, sendo assim, torna-se inconcebível que o conhecimento matemático seja abordado como um conhecimento em si mesmo sem referências consistentes com as diversas dimensões da realidade, portanto, indispensável que seja compreendido numa perspectiva sociopolítica (Souza, 2010).
Segundo os Parâmetros Curriculares Nacionais (1999) o ensino de matemática costuma provocar duas sensações contraditórias, tanto por parte de quem ensina como por parte de quem aprende: de um lado, a constatação de que se trata de uma área de conhecimento importante; de outro, a insatisfação diante dos resultados negativos obtidos com muita frequência em relação a sua aprendizagem.
Utilizando-se das novas tecnologias em sala há um movimento de avaliação permanente por parte do professor em relação ao aluno. A avaliação deve constituir de diversas condições e ritmos diferenciados, já que depende do avanço de cada aluno. Isso dá uma característica dinâmica à avaliação. O processo avaliativo acompanha o caráter dinâmico e espiralado da construção do conhecimento, assumindo diferentes dimensões e significado a cada etapa dessa construção. A relação professor/ aluno, via avaliação, é complexa e multidimensional à medida que representa, permanentemente, enviar e traduzir mensagens por ambas as partes. Cada um deles estará sempre interpretando o que ouve e o que observa do outro, tanto em relação ao processo de aprender, quanto ao próprio conteúdo de aprendizagem (Hoffmann, 2002).
É objetivo desse trabalho avaliar o ensino-aprendizagem da Geometria pelos alunos do ensino fundamental com o auxílio do software Wingeom. A presente proposta foi aplicada em 100 alunos do nono ano do curso fundamental de um colégio particular de São José dos Campos, SP, Brasil. Para avaliar o ganho educacional alcançado pelos alunos após essa intervenção, usamos o parâmetro D de Cohen (Cohen, 1992). Para se mensurar esse parâmetro, usando a técnica do pré-teste e do pós-teste (Gery, 1972).
O coeficiente D de Cohen (Cohen, 1977) é usado para estimar o tamanho do efeito da intervenção fornecida para os participantes do grupo experimental (COHEN, 1977; HALLAHAN et al., 1996; LOO KANG et al., 2015). O ganho educacional alcançado é calculado pelo método:

Com isso, é objetivo deste trabalho apresentar os resultados obtidos com a aplicação de uma proposta de ensino de geometria para a série final do Ensino Fundamental. A eficiência da intervenção didática foi medida usando os parâmetros D de Cohen e o <g> ganho educacional.
Com a evolução dos TICs - tecnologias da informação e comunicação, a sua inserção no ambiente escolar é inevitável. Nos tempos modernos necessita-se de informação rápida, atual e eficiente. Na era dos computadores, os alunos sentem essa mesma necessidade de informação, com isso surge à importância de unir educação e o ensino de novas tecnologias.
A prática educativa está se adaptando ao grande e rápido avanço tecnológico que está acontecendo no século XXI. Aos alunos é muito convidativa a tecnologia em geral. E a aula expositiva, muitas vezes acaba se tornando desinteressante. Nesse contexto, deve-se usar a tecnologia em favor do ensino. Segundo Ione (2002), o uso dos computadores deve ser associado ao conteúdo de matemática. As novas tecnologias representam uma transformação no modo de pensar e agir das pessoas, implicando numa mudança mais ágil, transparente e autônoma.
A escola precisa integrar-se no processo de modernização em que o mundo está passando e, muito mais que isso, criar oportunidades ao estudante de estabelecer uma relação de intimidade e confiança com essas novas tecnologias.
A informática em sala de aula exige do professor e do aluno certas habilidades em relação às novas tecnologias. Faz-se de extrema importância a formação continuada de educadores, para que haja maior entrosamento entre o computador e a matéria a ser aplicada. O computador na escola: mesmo que a informática já seja uma realidade irreversível, os educadores se sentem assustados e incertos. Sobre suas cabeças passam muitas falsas revoluções que embaralham os quadros de referência cultural, consolidados ao longo de décadas (Ione, 2002).
De acordo com o PCN (1999), esse impacto da tecnologia, cujo instrumento principal é o computador, exigirá do ensino de Matemática um redirecionamento sob uma perspectiva curricular que favoreça o desenvolvimento de habilidades e procedimentos com os quais o indivíduo possa se reconhecer e se orientar nesse mundo do conhecimento em constante movimento.
Ferreira (2013) aponta diversos resultados da aplicação de TICs no ensino da geometria. Um dos professores que aplicou esses recursos diz que isso torna as aulas dinâmicas e, principalmente na geometria, ilustra claramente determinados tópicos. Outro professor ressalta que os TICs facilita a realização de cálculos repetitivos, proporciona uma melhor visualização de gráficos e de figuras geométricas, os objetos de aprendizagem podem estimular o aluno a responder e fazer conjecturas.
Dentre os softwares criados para servirem de ferramenta do ensino da geometria encontram-se os desenvolvidos pela Peanut Software. O professor Richard Parris desenvolveu uma família de nove softwares, todos com o objetivo de auxiliar o ensino da geometria. Os softwares desenvolvidos apresentam uma boa resolução gráfica, em português e são disponíveis na internet inteiramente grátis e pode ser baixados (download) através do site http://math.exeter.edu/rparris.
A família é composta pelos seguintes programas:
http://www.gregosetroianos.mat.br/softwinplot.asp
Este trabalho abordará as características do software Wingeom como ferramenta no ensino da geometria.
A pesquisa foi desenvolvida com cem alunos do último ano do ensino fundamental (nono ano) de uma escola particular de São José dos Campos. Durante nove semanas, os alunos tiveram acompanhamento semanal durante as aulas de geometria.
A primeira parte da pesquisa foi realizada na sala de informática que dispõe de vinte computadores. Durante as três primeiras semanas, os alunos conheceram o software e desenvolveram atividades com os conceitos básicos de geometria, como construção de retas, semirretas, segmentos de reta, polígonos convexos, polígonos côncavos, cálculo de perímetro, área e etc.
As três primeiras aulas, no laboratório de informática, tiveram como tema:
I. Apresentação do software, utilização dos comandos básicos e uma atividade de identificação de arestas, faces e vértices em polígonos regulares.
II. Construção na tela 2D polígonos e cálculo de área, perímetro e a construção de diagonais de um polígono regular.
III. Construção de um poliedro através de suas coordenadas, criando assim os vértices, as arestas e por fim as faces.
Após três aulas com o Wingeom, foi realizado o pré-teste, onde o objetivo foi identificar a familiarização do aluno com a geometria. O teste foi composto de treze exercícios e os alunos tiveram cinquenta minutos para a realização do mesmo.
Após o teste, aulas teóricas foram expostas no decorrer de três semanas, onde foram revistos conceitos geométricos e apresentado outros inéditos, resolução de problemas geométricos e etc. Nas aulas teóricas, que tiveram como conteúdo desde os elementos de um polígono regular, a soma dos ângulos internos, o número de diagonais, o perímetro de polígonos inscritos em circunferências e cálculo de apótemas. No desenvolvimento dessas aulas a utilização do Wingeom não foi suspensa, foi utilizado para criar os polígonos que eram descritos em sala.
O segundo teste foi aplicado após as aulas conceituais e teve como objetivo identificar a construção de conceitos, a identificação de figuras geométricas e a sua representação. Esse teste foi composto por oito exercícios e os alunos também tiveram cinquenta minutos para concluí-lo. O cronograma é apresentado na Tabela 1.
Tabela 1 – Cronograma da aplicação da metodologia.
Semana Atividade |
1ª |
2ª |
3ª |
4ª |
5ª |
6ª |
7ª |
8ª |
9ª |
Aulas com o Wingeom |
|
|
|
|
|
|
|
|
|
Pré-Teste |
|
|
|
|
|
|
|
|
|
Aulas Teóricas |
|
|
|
|
|
|
|
|
|
Pós-Teste |
|
|
|
|
|
|
|
|
|
Na correção dos testes aplicados três classificações quanto às respostas foram consideradas: certa, errada ou meio certa. A questão será considera certa quando o aluno conseguir atingir os objetivos; errada quando não conseguir; e, meio certa quando atingir parte dos objetivos. Durante todo o desenvolvimento da pesquisa, as aulas do Wingeom continuaram de acordo com a atividade desenvolvida em sala, visualizavam-se as imagens com o auxílio do Wingeom.
Os resultados dos testes aplicados em duas etapas foram compilados, tabelados e sintetizados na forma de gráficos e estão apresentados adiante. Para comparação entre os testes, uma equivalência entre as questões foram estabelecidas para estimar a evolução do aprendizado. Essa equivalência é apresentada na Tabela 2.
Tabela 2 – Equivalências dos testes aplicados em duas etapas.
|
TESTE 1 |
TESTE 2 |
Figura 1 |
1 e 2 |
1 |
Figura 2 |
3 |
7 |
Figura 3 |
4 |
5 |
Figura 4 |
5 |
3 |
Figura 5 |
10 e 11 |
6 |
Figura 6 |
7 e 13 |
8 |
Figura 7 |
9 |
4 |
Outras questões que não apresentavam equivalência significativa foram analisadas individualmente. Isso ocorreu com as questões seis, oito e doze do primeiro teste e com a questão dois do segundo teste.
Na Figura 1 foi analisado o resultado das questões um e dois do teste um, essas questões tinham como tema figuras planas e/ou espaciais. Os resultados indicam que os alunos já possuíam uma boa base (Teste 1) e que com as aulas teóricas tiveram um singela melhora.

Fig. 1 – Identificação de figuras planas ou espaciais.
Na Figura 2 é apresentada o resultado das questões três do primeiro teste com a questão sete do segundo. Estas questões eram de caráter conceitual onde os alunos deveriam ser capazes de calcular o número de lados de polígonos ou poliedros ou determinar o número de diagonais dos mesmos.
Nessas questões os alunos deveriam utilizar um conceito já estruturado para resolver o problema. Após as aulas teóricas, os alunos demonstram maior aptidão nos conceitos geométricos.
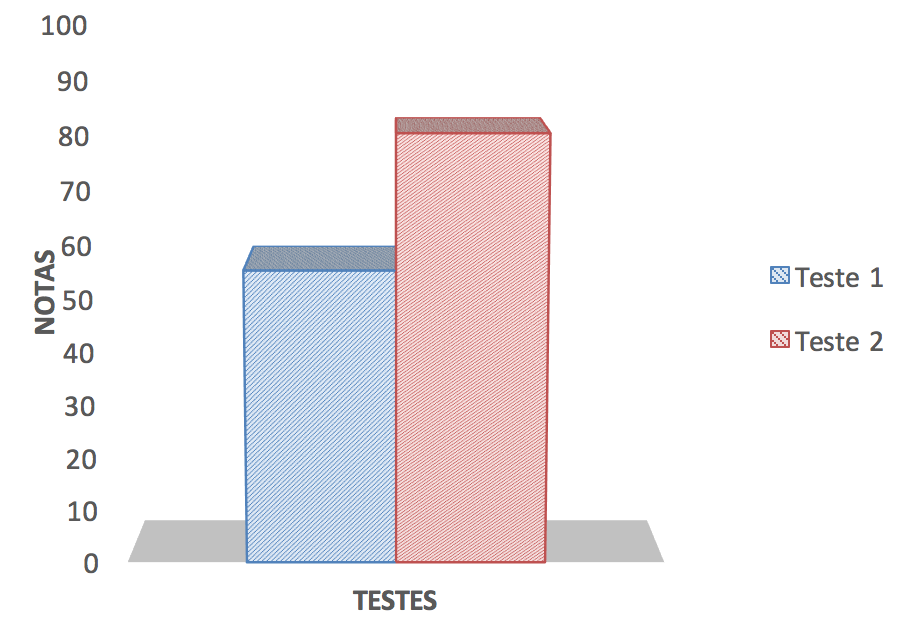
Fig. 2 – Assimilação de conceitos geométricos.
Na Figura 3 três foi analisado as questões quatro do primeiro teste e cinco do segundo teste. Estas questões eram de caráter visual, ou seja, era necessário que o aluno identificasse através da imagem do poliedro ou do polígono o que se pedia para a solução do problema. Com o auxílio do Wingeom, os alunos tiveram maior aproveitamento devido à facilidade em visualizar a figura em três dimensões. Contudo, após o embasamento teórico, os alunos apresentaram maior progresso neste aspecto.

Fig. 3 - Visualização de Polígonos ou poliedros.
A Figura 4 apresenta a relação entre a questão cinco do primeiro teste com a três do segundo. Estas questões eram de caráter conceitual, o aluno deveria ser capaz de nomear os polígonos ou poliedros corretamente. Outro critério analisado foi a de determinar ou identificar o polígono através de algumas características como o número de diagonais. A melhora foi considerável.

Fig. 4 – Absorção de conceitos geométricos
As questões dez e onze do primeiro teste relacionam-se com a questão seis do segundo teste e são apresentados como resultado na Figura 5. Eram questões de caráter conceitual na qual o aluno deveria ser capaz de determinar a área e o perímetro de determinados polígonos. Com o Wingeom, os alunos tiveram maior facilidade de visualização e cálculo através do próprio programa. Entretanto, nas questões efetuadas pelo aluno ocorreram erros algébricos. Aqui desponta uma interrogação, o quanto é verdadeiro esse progresso se no cálculo algébrico erros forma cometidos?
Após as aulas teóricas, os alunos conseguiram um avanço significativo, grande parte proveniente das dúvidas sanadas quanto à parte algébrica.
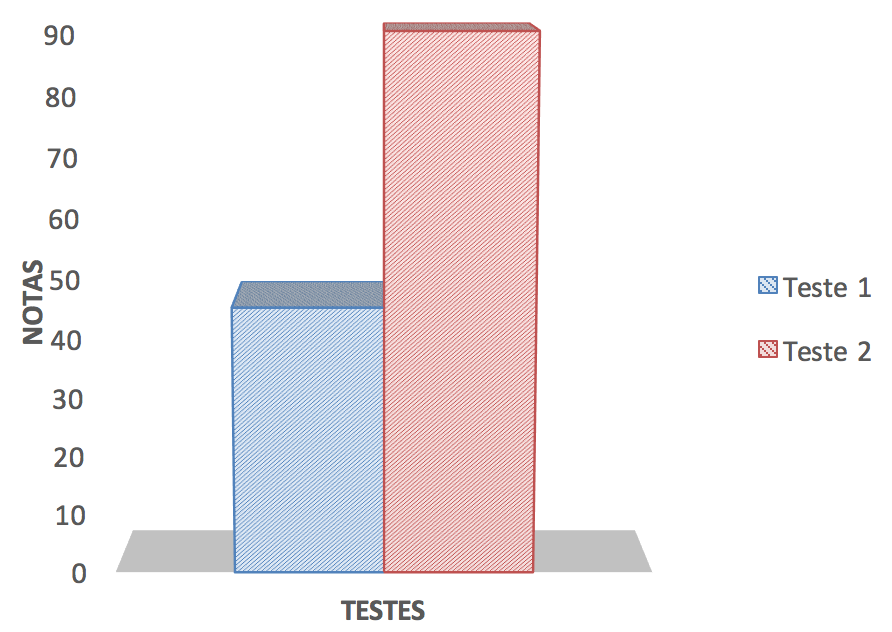
Fig. 5 – Cálculo de perímetro e áreas
Na Figura 6 são apresentados os resultados das questões sete e treze do primeiro teste com a questão oito do segundo teste. Estas questões são de caráter usual, ou seja, o aluno deveria ser capaz de utilizar a geometria para identificar situações do cotidiano.
Na questão do primeiro teste, os alunos não atingiram todos os objetivos da questão como, por exemplo, desenhar os lados ocultos de um tijolo ou a base circular de uma lata de refrigerante. Esses objetos poderiam ser associados respectivamente a um prisma de base quadrada e a um cilindro. Nessa questão deve-se também levar em consideração as habilidades artísticas de cada aluno. Entretanto, os resultados foram positivos após a intervenção com o software e com as aulas teóricas.
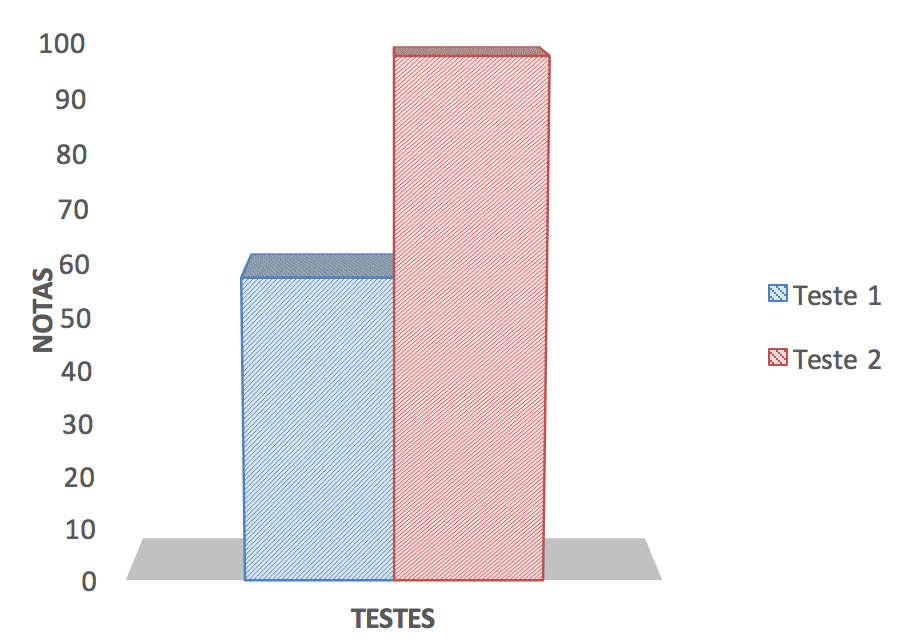
Fig. 6 – Utilização da geometria no cotidiano.
Na Figura 7 são apresentados os resultados da questão nove do primeiro teste em relação à questão quatro do segundo teste. Estas questões eram consideradas de caráter conceitual na qual o aluno deveria ser capaz de construir retas paralelas e diagonais. No primeiro teste, muitos erros derivaram de conceitos mal estruturados.
Na segunda parte da pesquisa com as aulas teóricas somadas com o Wingeom, os alunos conseguiram contextualizar os conceitos expostos em sala.

Fig. 7 – Contextualização dos conceitos geométricos.
A seguir serão apresentadas as questões que foram analisadas individualmente por não possuírem equivalência entre os testes.
Na Figura 8 é apresentado o resultado da questão seis do primeiro teste, que consiste em dar as coordenadas de pontos dispersos em um sistema cartesiano. A maioria dos alunos teve sucesso nessa questão, os erros ocorreram na maior parte por falha na contagem da escala nos eixos “x” e “y”.
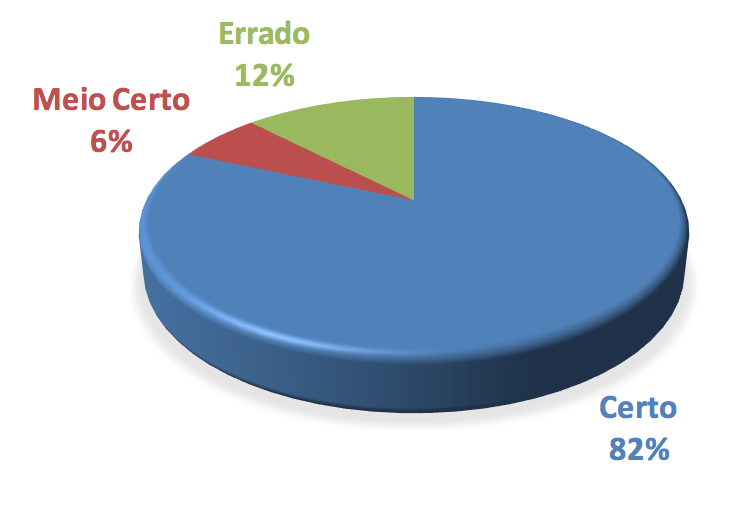
Fig. 8 – Identificação de pontos do Sistema Cartesiano
A Figura 9 apresenta o resultado da questão oito do primeiro teste, era solicitado aos alunos que representassem (desenhar) um cubo. Foi considerada uma questão errada os desenhos de outros poliedros (cone ou cilindros) ou alunos que desenharam uma figura plana (quadrado). Alguns alunos não atingiram todos os objetivos, desenhando de forma errônea as arestas ocultas deste cubo (10%). 60% dos alunos desenharam corretamente o cubo e 30% dos alunos atingiram parcialmente o objetivo da questão.
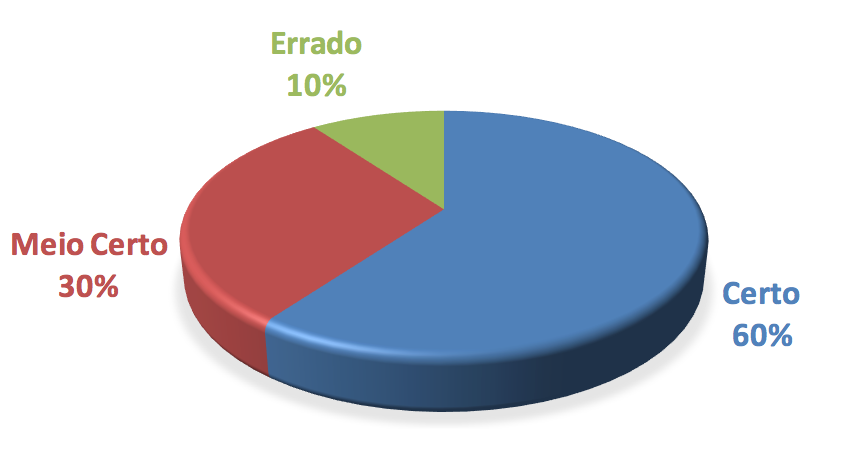
Fig. 9 – Representação do cubo
Na Figura 10 é apresentado o resultado na análise da questão doze do primeiro teste, onde foi solicitado aos alunos que construíssem a bissetriz de um ângulo qualquer. Foi considerada como questão correta todas as que apresentaram características de uma reta que “cortassem” o ângulo ao meio, mesmo que não fosse de modo exato. Boa parte dos alunos obteve êxito nesse quesito.

Fig. 10 – Construção de uma bissetriz
Na Figura 11 é apresentada o resultado da questão dois do segundo teste, os alunos deveriam ser capazes de identificar qual a medida do ângulo interno e a soma dos ângulos internos de um polígono regular. Ocorreram dois tipos de erros, primeiro os algébricos no qual os alunos erravam na efetuação dos cálculos e, os erros de características conceituais, errando nas fórmulas. Boa parte dos alunos realizaram corretamente os procedimentos (70%).

Fig. 11 – Calculo da Soma dos ângulos internos e medida dos ângulos internos.
A fim de avaliar a intervenção pedagógica aplicada, mensuramos o ganho educacional <g> e o parâmetro D de Cohen. Para o pré-teste, obtivemos médias ![]() para o pré-teste e pós-teste, respectivamente.
para o pré-teste e pós-teste, respectivamente.
Para a análise da evolução educacional obtida pelos alunos ao longo da prática de laboratório, usamos o parâmetro D de Cohen (Cohen, 1992), que com base nos dados obtidos corresponde a 1,2, que corresponde a um ganho educacional grande segundo Cohen. O ganho educacional <g> mensurado para essa pesquisa foi de 0,56, que está avaliado como sendo um ganho médio.
Na Figura 12 é apresentada a distribuição de frequência de notas dos alunos no pré e pós-teste. Podemos observar pelo gráfico que houve uma evolução das notas após a combinação dos trabalhos teóricos com o do software Wingeom.

Fig. 12 – Diagrama de correlação entre o ganho educacional e os testes aplicados.
Em um contexto geral, o Wingeom se mostrou uma importante ferramenta no ensino e aprendizagem dos alunos, que ao fim do projeto se apresentaram com uma melhora significativa em diversas categorias da geometria.
O Wingeom auxiliou os alunos na visualização dos polígonos e poliedros, fixando os conceitos vistos em sala de aula. Com a facilidade da visualização em três dimensões, os erros eram minimizados o que em uma aula tradicional seria dificultado.
A construção de conceitos através do software não era assimilada com eficácia, talvez pelo fato de o uso do computador facilitar a realização dos exercícios. Essas lacunas na aprendizagem dos alunos foram supridas com as aulas teóricas, indicando a necessidade das aulas formais (tradicionais).
A melhora dos alunos na construção de conceitos e identificação de polígonos e poliedros é atribuída a diversos fatores, entre eles a construção de conceitos na aula tradicional somados com a facilidade de visualização oferecidos pelo Wingeom.
O software se comportou como uma ferramenta no ensino-aprendizagem dos alunos, isso contribuiu para que os alunos conseguissem transportar os conhecimentos geométricos para o seu dia-a-dia e torna-se assim a geometria usual.
A métrica D de Cohen e o ganho educacional <g> refletiram a evolução dos alunos com valores: 1,2 e 0,56 respectivamente.
P. FREITAS-LEMES agradece a CAPES pelo apoio financeiro.
COHEN, J. Statistical power analysis for the behavioral sciences (rev. ed.). Academic Press. New York, p. 357-410, 1977.
_________ A power primer. New York University. Psychological Bulletin, 112, 155‐159. 1992.
FERREIRA, F. P. O Uso das TIC’s nas aulas de matemática na perspectiva do professor. TCC. FEG-GUARATINGUETÁ. 2013.
FREIRE, P. Pedagogia do Oprimido. Rio de Janeiro: Paz e Terra, Freire, 2002.
GERY, F. W. Does mathematics matter? Research papers in economic education, p. 142-157, 1972.
HAKE, R. R. Interactive-engagement versus traditional methods: A six-thousand-student survey of mechanics test data for introductory physics courses. American journal of Physics, v. 66, n. 1, p. 64-74, 1998.
_________Relationship of individual student normalized learning gains in mechanics with gender, high-school physics, and pretest scores on mathematics and spatial visualization. Physics Education Research Conference (Boise), ID, 2002.
HALLAHAN, M.; ROSENTHAL, R. Statistical power: Concepts, procedures, and applications. Behaviour research and therapy, v. 34, n. 5, p. 489-499, 1996. ISSN 0005-7967.
HOFFMANN, Jussara. Avaliar para promover: as setas do caminho. Porto Alegre: Mediação, 2002.
LOO KANG, W. et al. Using Tracker to understand ‘toss up’ and free fall motion: a case study. Physics Education, v. 50, n. 4, p. 436, 2015.
PARRIS, R. Softwares do Peanut. Disponível em HTTP://math.exeter.edu/rparris. Acessado em 15 de setembro de 2012.
________. Parâmetros Curriculares Nacionais. Brasília MEC/ SEMTEC, 1999.
SOUZA, N. F. Roseira, N. A. F. A contextualização no processo de ensino aprendizagem da matemática. XVI Jornada Regional de Educação matemática. UPF. 2010.
1. ITA - Instituto Tecnológico de Aeronáutica, UNIVAP – Universidade do Vale do Paraíba, 12244-000 - São José dos Campos – SP. Email: piprisc@gmail.com
2. ITA - Instituto Tecnológico de Aeronáutica, 12228-900 - São José dos Campos - SP
3. ITA - Instituto Tecnológico de Aeronáutica, 12228-900 - São José dos Campos - SP
4. UNIVAP – Universidade do Vale do Paraíba, 12244-000 - São José dos Campos – SP
5. UNIVAP – Universidade do Vale do Paraíba, 12244-000 - São José dos Campos – SP