

Vol. 38 (Nº 41) Año 2017. Pág. 16
Gabriel Alberto AGUDELO-Torres 1; Luis Ceferino FRANCO-Arbeláez 2; Luis Eduardo FRANCO-Ceballos 3; Nora GAVIRA Durón 4
Recibido: 06/04/2017 • Aprobado: 12/05/2017
2. Condición de Hamilton – Jacobi – Bellman, programación dinámica determinista
3. Condición de Hamilton – Jacobi – Bellman, programación dinámica determinista actuarial
RESUMEN: El objetivo principal de un consumidor racional que cuenta con una dotación inicial de riqueza, es la asignación de esos recursos al consumo y a la inversión distribuida entre los diferentes activos disponibles en los mercados financieros. En este artículo se utiliza la técnica de programación dinámica en tiempo continuo, basada en la ecuación de Hamilton-Jacobi-Bellman (H-J-B), para resolver dicho problema de optimización tanto en su forma determinista como en su forma determinista actuarial. Se demuestra que no es necesario el supuesto tradicional de vida infinita del consumidor, o su equivalente: una preocupación por la maximización del consumo futuro propio y de sus generaciones futuras, ya que, sin esa condición, los resultados son idénticos utilizando el valor presente del consumo y utilizando el valor presente actuarial del mismo. |
ABSTRACT: The main goal of a rational consumer with an initial endowment of wealth is the allocation of these resources to consumption and investment distributed among different assets available in financial markets. This paper uses the Continuous-Time Dynamic Programming technique based on the Hamilton-Jacobi-Bellman (H-J-B) equation for solving said optimization problem both in its deterministic and actuarial-deterministic form. It is demonstrated that the traditional assumption of customer’s infinite lifetime —or its equivalent, a concern for the maximization of his/her future consumption and the consumption of his/her future generations—, is irrelevant, since, without that condition, results remain identical using the current consumption and actuarial values. |
El objetivo principal de un consumidor racional que cuenta con una dotación inicial de riqueza, es la asignación de esos recursos al consumo y a la inversión distribuida entre los diferentes activos disponibles en los mercados financieros. En este artículo se utiliza la técnica de programación dinámica en tiempo continuo, basada en la ecuación de Hamilton-Jacobi-Bellman (H-J-B), para resolver dicho problema de optimización tanto en su forma determinista como en su forma determinista actuarial. Se demuestra que no es necesario el supuesto tradicional de vida infinita del consumidor, o su equivalente: una preocupación por la maximización del consumo futuro propio y de sus generaciones futuras, ya que, sin esa condición, los resultados son idénticos utilizando el valor presente del consumo y utilizando el valor presente actuarial del mismo.
La literatura sobre decisiones de consumo y portafolio bajo el criterio de maximización de utilidad tiene su origen en los artículos de Merton (1969) y (1971) en los cuales el movimiento browniano se utiliza para modelar el riesgo de mercado.
En cuanto a las preferencias por consumo e inversión de los agentes, Lucas (1978) y Breeden (1979) suponen que dichas preferencias tienen una representación igual a la utilizada por Von-Neummann y Morgenstern (1944). Posteriormente, Harrison y Kreps (1979), y Harrison y Pliska (1981) relacionan el concepto de martingala con el problema de decisión de un consumidor-inversionista racional, permitiendo que la solución del problema de optimización se presente a través de un proceso de precios.
Por otra parte, Lions (1983) analiza los problemas de control estocástico óptimo general y las ecuaciones Hamilton-Jacobi-Bellman asociadas a ellos, desarrollando una noción general de soluciones débiles llamadas soluciones de viscosidad y agrega una demostración de la estabilidad de estas soluciones.
Dolcetta (1983) propone una aproximación de la ecuación de Hamilton-Jacobi-Bellman relacionada con el problema de control óptimo del horizonte infinito con descuento, lo cual coincide con el problema del consumidor inversionista con vida infinita. Además, muestra que las soluciones aproximadas convergen uniformemente a la solución de viscosidad planteada por Lions (1983), en el sentido de Crandall-Lions (1983).
Peng (1992) estudia la ecuación diferencial parcial estocástica no lineal, donde introduce coeficientes y resultados aleatorios. La ecuación clásica Hamilton-Jacobi-Bellman (HJB) puede considerarse como un caso especial de este problema.
En las últimas décadas varios investigadores han avanzado en la solución de la ecuación de Hamilton-Jacobi-Bellman. Zariphopoulou (1994) examina un problema general de inversión y consumo para un solo agente que consume e invierte en activos libres de riesgo y en activos con riesgo; agrega restricciones de negociación, endeudamiento limitado y la no bancarrota, y formula el problema de optimización como un problema de control estocástico con restricciones de estado y control. Li, Zhou y Lim (2002), trabajan en los problemas de selección de cartera de media varianza en tiempo continuo bajo la restricción de que la venta corta de acciones está prohibida y Schmidli (2002) desarrolla una solución para el caso en el que el consumidor puede invertir en un reaseguro.
En cuanto a la modelación del precio de los activos, múltiples investigaciones han abordado el estudio de fenómenos financieros considerando su dinámica estocástica. Algunos trabajos seminales con este tipo de este enfoque son Black y Scholes (1973), Merton (1973), Vasicek (1977), y Cox Ingersoll y Ross (1985a) y (1985b). Venegas-Martínez, Agudelo, Franco y Franco (2016) analizan el comportamiento de un activo conducido en varias regiones por Procesos de Itô Económicamente Ponderados. Otros trabajos que generalizan los Procesos de Itô para el modelamiento del precio de activos se encuentran en Grinols y Turnovsky (1993) y Schmedders (1998). Como lo plantean Agudelo, Franco, Franco y Olivares (2016), cada vez se tienen nuevos y más complejos instrumentos financieros, para los cuales es necesario modelar sus potenciales comportamientos, y tener herramientas útiles como soporte para diversas decisiones financieras sujetas a la incertidumbre y al riesgo.
La Función de Gasto en Consumo es introducida por Keynes (1936) al considerar que el nivel de consumo está directamente relacionado con la renta. Duesenberry (1949) sostiene que la función de consumo no es proporcional al ingreso, pues al paso del tiempo el consumo reacciona de forma más suave a la variación del ingreso, debido a que el consumo depende tanto del ingreso actual como del ingreso obtenido en el pasado reciente; la formalización de este concepto fue llamada Función de Gasto en Consumo Relativo. Modigliani y Brumberg (1954) introducen la función de Renta del Ciclo Vital, sosteniendo que el consumo depende de todo el ciclo de vida del individuo, no solo del pasado reciente. Por su parte, Friedman (1957) para el análisis incluye la renta que los individuos pueden obtener en el futuro en su Función de Consumo de Renta Permanente.
En años recientes, Hernández-Núñez (2014) utiliza el concepto de curvas de indiferencia de la utilidad para mostrar que a medida que aumenta el ingreso, el nivel de consumo no aumenta al mismo ritmo (saciedad), y concluye que el consumo es una función creciente a tasas decrecientes. Por lo tanto, las funciones más adecuadas para analizar el consumo son las que tienen utilidad logarítmica.
Después de esta introducción, en la Sección 2, se resuelve el problema intertemporal de decisión de consumo en un ambiente determinista. En la Sección 3, se resuelve el mismo problema, pero en un ambiente determinista actuarial; es decir, incluyendo en su solución la probabilidad de vivir del individuo en cada instante. Finalmente, se presentan las conclusiones y futuras líneas de investigación.
Para resolver el problema intertemporal de decisión de un consumidor racional, preocupado por su bienestar y el de su descendencia, o bien de un consumidor racional con vida infinita, se considera la siguiente función de utilidad

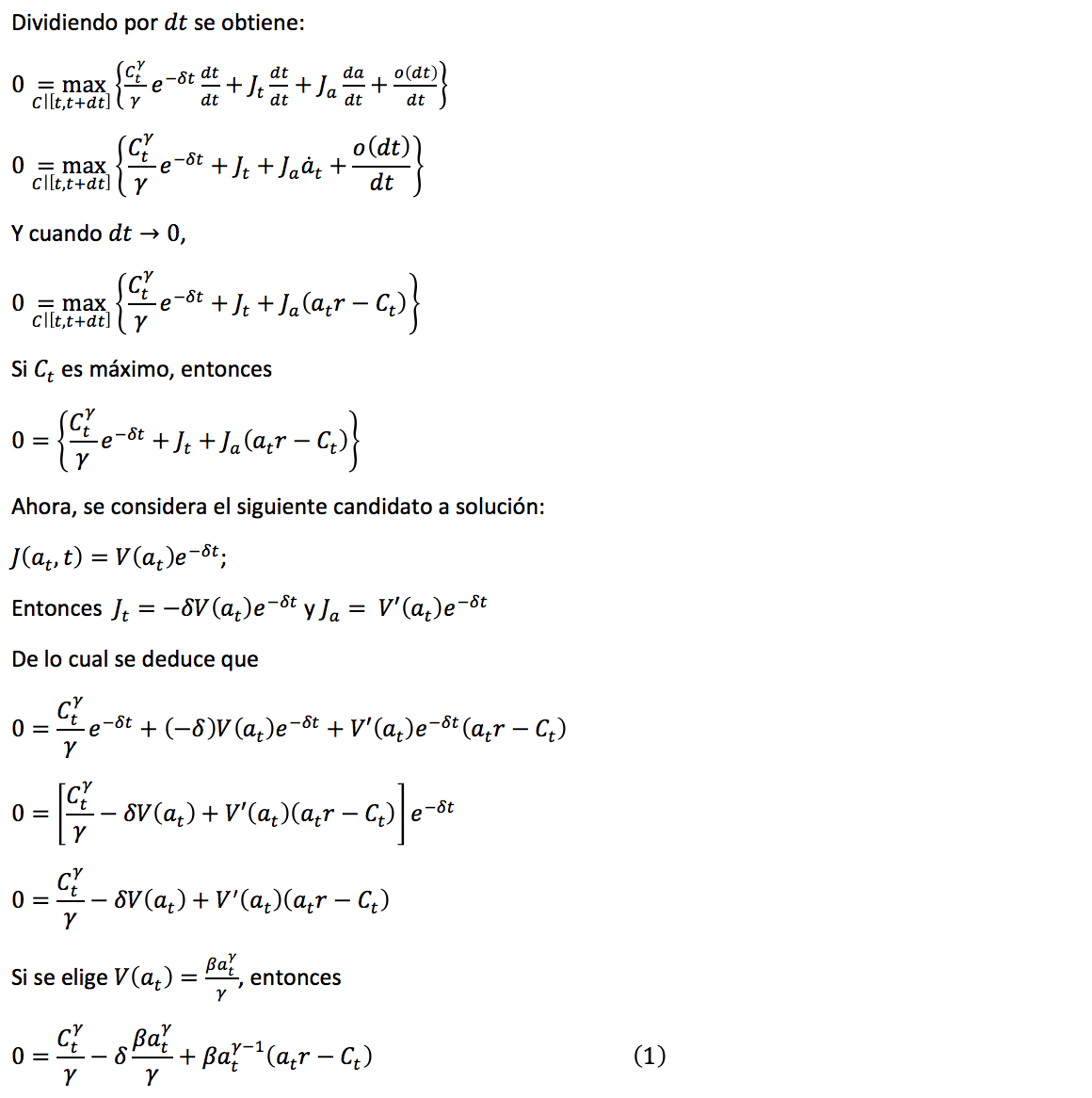


En esta sección se considera el problema de optimizar el valor presente actuarial de la función de consumo utilizada en la sección anterior, pero corregida por la probabilidad de que el individuo de edad x alcance una determinada edad en el futuro; es decir, se evalúa el valor presente actuarial de los consumos futuros.


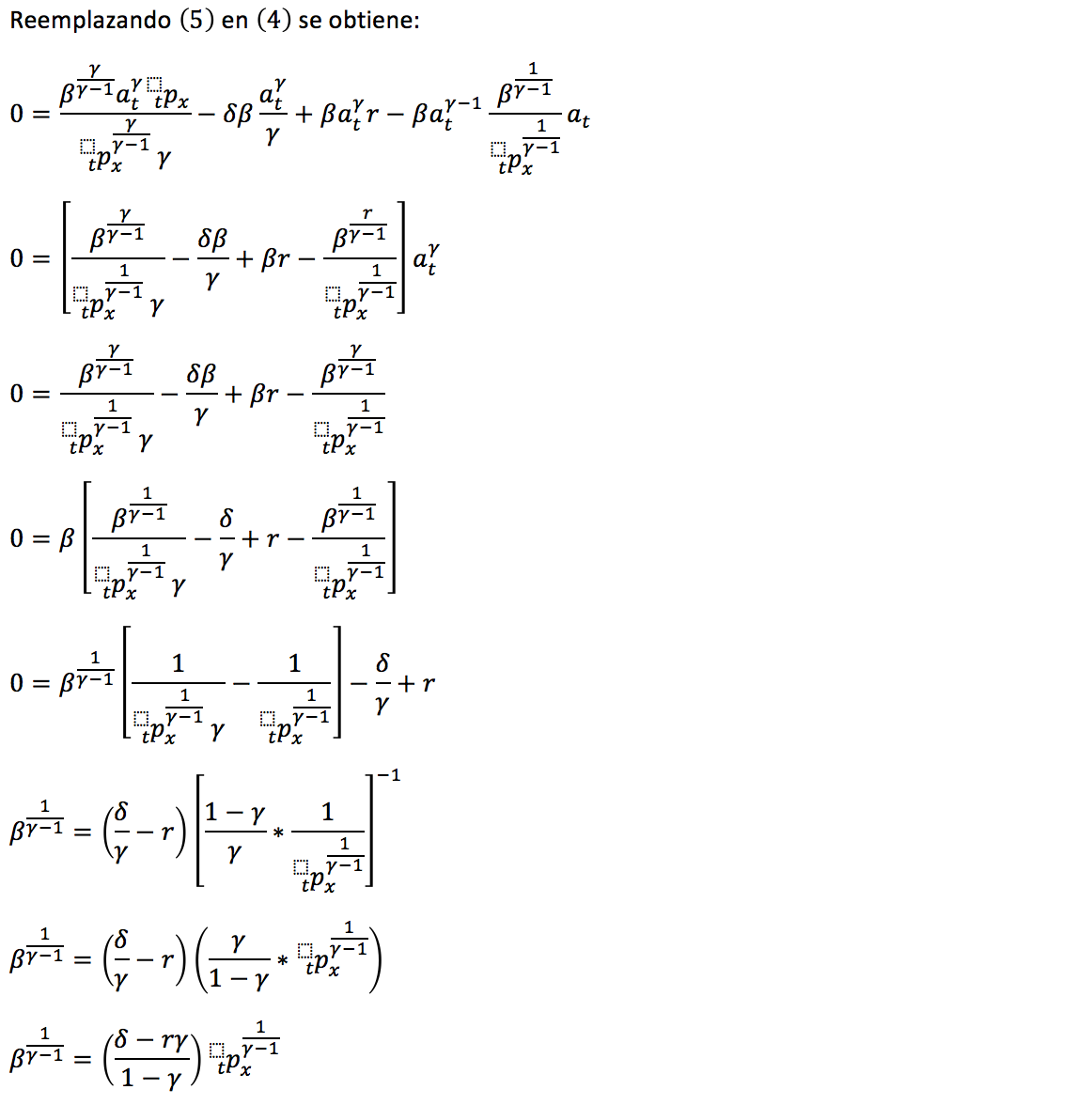

Tradicionalmente el problema referente a la asignación de recursos al consumo y a la inversión de un individuo racional que cuenta con una dotación inicial de riqueza, incluye el supuesto de vida infinita del consumidor o una preocupación por la maximización del consumo propio y de sus generaciones futuras. En esos modelos ignorar ese supuesto implica un conocimiento previo del momento de muerte del individuo o del fin de su consumo.
En este artículo se utiliza la técnica de programación dinámica en tiempo continuo, basada en la ecuación de Hamilton-Jacobi-Bellman, para resolver dicho problema de optimización tanto en su forma determinista como en su forma determinista actuarial. Se demuestra que los supuestos antes mencionados no son necesarios, pues los resultados son idénticos utilizando el valor presente del consumo y utilizando el valor presente actuarial del mismo.
Investigaciones futuras pueden estar orientadas a determinar la relevancia de este supuesto al resolver el problema mediante la Utilidad Diferencial Recursiva Estocástica (UDRE), técnica utilizada, en la especificación, para separar la aversión al riesgo y la sustitución intertemporal al consumo.
Agudelo, G.A., Franco, L.C., Franco, L.E., Olivares, H, A. (2016). Cálculo Estocástico Aplicaciones en Finanzas. Colombia: Optimal Research SAS. ISBN: 978-958-95363-5-3, 1 ed.
Black, F. and M. Scholes (1973). The Pricing of Option and Corporative Liabilities. Journal of Political Economy, Vol. 81, No 3, pp. 637-654.
Breeden, D. (1979). An Intertemporal Asset Pricing Model with Stochastic Consumption and Investment Opportunities. Journal of Financial Economics, Vol. 7, pp. 265-296.
Cox, J., J. Ingersoll y S. Ross (1985a). An Intertemporal General Equilibrium Model of Asset Prices, Econometrica, Vol. 53, No. 2, pp. 385-467.
Cox, J., J. Ingersoll y S. Ross (1985b). A theory of the term structure of interest rates, Econometrica, Vol. 53, No. 2, pp. 385-467.
Crandall, M. G. y Lions, P. L.(1983). Viscosity solutions of Hamilton-Jacobi equations, Trans. Amer. Math. Soc., 277, 1-42.
Dolcetta, I. C. (1983). On a discrete approximation of the Hamilton-Jacobi equation of dynamic programming. Applied Mathematics & Optimization, 10(1), 367-377.
Duesenberry, J. S. (1949). Income. Saving and the Theory of Consumer Behavior, Harvard: Cambridge.
Friedman, M. (1957). The permanent income hypothesis. In A theory of the consumption function (pp. 20-37). Princeton University Press.
Grinols, E. L. y S. J. Turnovsky (1993). Risk, the Financial Market, and Macroeconomic Equilibrium, Journal of Economic Dynamics and Control, Vol. 17, No. 1-2, pp. 1-36.
Harrison, J. M. and D. M. Kreps (1979), Martingales and Arbitrage in Multiperiod Security Markets, Journal of Economic Theory, Vol. 20, No. 3, pp. 381-408.
Harrison J. M. and S. R. Pliska (1981), Martingales and Stochastic Integrals in The Theory of Continuous Trading, Stochastic Processes and their Applications, Vol. 11, No. 3, pp. 215-260.
Hernández Núñez, R.J. (2014). La Función de Gasto en consumo.
Keynes, J. M. (1936). The general theory of employment, interest and money. London, 1936. KeynesThe General Theory of Employment, Interest and Money1936.
Li, X., Zhou, X. Y., & Lim, A. E. B. (2002). Dynamic mean-variance portfolio selection with non-shorting constraints. SIAM Journal on Control and Optimization, 40(5), 1540-1555.
Lions, P. L. (1983). Optimal control of diffusion processes and hamilton-jacobi-bellman equations. Communications in Partial Differential Equations, 8(11), 1229-1276.
Lucas, R. (1978). Asset Prices in an Exchange Economy. Econometrica, Vol. 46, pp. 1429-1445.
Merton, R. C. (1969). Lifetime Portfolio Selection under Uncertainty: the Continuous-time Case, Review of Economics and Statistics, Vol. 51, No. 3, pp. 247-257.
Merton, R. C. (1971). Optimum Consumption and Portfolio Rules in a Continuous-Time Model, Journal of Economic Theory, Vol. 3, No. 4, pp. 373-413.
Merton, R. (1973). Theory of Rational Option Pricing. Bell Journal of Economics, Vol. 4, No. 1, pp. 141-183.
Modigliani, F., & Brumberg, R. (1954). Utility analysis and the consumption function: An interpretation of cross-section data. Franco Modigliani, 1.
Peng, S. (1992). Stochastic Hamilton-Jacobi-Bellman equations. SIAM Journal on Control and Optimization, 30(2), 284-304.
Schmedders, K. (1998). Computing Equilibria in the General Equilibrium Model with Incomplete Asset Markets. Journal of Economic Dynamics and Control, Vol. 22, No. 8-9, pp. 1375-1401.
Schmidli, H. (2002). On minimizing the ruin probability by investment and reinsurance. Annals of Applied Probability, 12(3), 890-907.
Vasicek O. (1977). An equilibrium characterization of the term structure. Journal of Financial Economics 5: 177-188.
Zariphopoulou, T. (1994). Consumption-investment models with constraints.SIAM Journal on Control and Optimization, 32(1), 59-85.1. Instituto Tecnológico Metropolitano, Medellín, Colombia. Email: albertoagudelo@itm.edu.co
2. Instituto Tecnológico Metropolitano, Medellín, Colombia. Email: luisfranco@itm.edu.co
3. Instituto Tecnológico Metropolitano, Medellín, Colombia. Email: luisefranco@itm.edu.co
4. Universidad de las Américas Puebla, Cholula, México. Email: nora.gavira@udlap.mx