

Vol. 38 (Nº 39) Año 2017. Pág. 16
Sonia JARAMILLO-VALBUENA 1; Jorge Mario LONDOÑO-PELÁEZ 2; Sergio AUGUSTO CARDONA 3
Recibido: 26/03/2017 • Aprobado: 23/04/2017
2. Concept drift detection methods
ABSTRACT: Many real-world applications generate massive amount of data that are continuous. This kind of data is known as streams. Sensor data, web logs, smart devices, phone records, social networks and ATM transactions are examples of sources of data streams. Typically, data streams evolve over time; this is referred to as concept drift. This phenomenon creates new challenges not present in classical machine learning techniques. In this paper, we compare 4 different methods to detect concept drift from data streams and determine their robustness in the presence of noisy data. We conducted a set of experiments on synthetic and real-world datasets. Finally, we present the results and suggest possible directions for future work. |
RESUMEN: Muchas aplicaciones del mundo real generan gran cantidad de datos que son continuos. Este tipo de datos se conoce como streams. Los datos de sensores, registros web, dispositivos inteligentes, registros telefónicos, redes sociales y transacciones ATM son ejemplos de fuentes de streams de datos. Típicamente, los streams de datos evolucionan con el tiempo; esto se conoce como concept drift. El concept drift crea nuevos desafíos que no están presentes en las técnicas clásicas de aprendizaje automático. En este trabajo, se comparan 4 diferentes métodos para detectar concept drift en streams de datos y se determina su robustez en presencia de ruido. Se realizan experimentos sobre datasets sintéticos. Finalmente, se presentan los resultados y se sugieren posibles direcciones para trabajos futuros. |
Big data generates million data per day in streamed manner. Streaming data pose challenging research problems in order to respond to tasks such as statistics maintenance, storage, real time querying and pattern discovery (Gama J. ). The real time processing poses important challenges. The classical machine algorithms have to be adapted to analyze huge amounts of streaming data on-the-fly and consider the presence of noise and the evolving nature of the stream (Fang Chu, 2005) (Le, Stahl, Gomes, Medhat Gaber, & Di Fatta, 2014). The latter will be referred to as concept-drift.
The term “concept drift” means that the statistical properties of the target concept change arbitrarily over time (Widmer & Kubat, 1996) (Wang, Yu, & Han, 2010) (Minku & Yao, 2012), causing the previously constructed model become less accurate and requiring an update or to be replaced with a new one (Wang, Yu, & Han, Mining Concept-Drifting Data Streams, 2010) (Dongre & Malik, 2014). In (Kelly, Hand, Adams, & M., 1999) indicate that depending on the nature of the concept drift, it can occur in three different ways:
An important challenge for Concept Drift Detection algorithms is to distinguish the occurrence of noise (random deviations or statistical anomalies) in the data from concept drift (Chandola, Banerjee, & Kumar, 2009). There are several approaches designed to identify concept drift. In this paper, we evaluate the performance of 4 of them in the presence of noise. We choose the Drift Detection Method (DDM) (Gama J. , Medas, Castillo, & Rodrigues, 2004), the Early Drift Detection Method (EDDM) (Baena-Garcia, et al., 2006), a drift detection method based on Geometric Moving Average Test (Roberts, 2000) and the Exponentially Weighted Moving Average Chart Detection Method (EWMAChartDM) (Del Castillo, 2001) (Ross, Adams, Tasoulis, & Hand, 2012).
The paper is organized as follows. Section 2 describes the methods evaluated. Section 3 reviews related works on performance evaluation of concept drift detection techniques in the presence of noise. Section 4 describes the experiments and analysis carried out in this study. The last section provides a summary of the findings in this work.
In this section we describe 4 known algorithms to detect concept drift: DDM, EDDM, GeometricMovingAverageDM and EWMAChartDM.
The Drift Detection Method (DDM) proposed in (Gama J. , Medas, Castillo, & Rodrigues, 2004) uses a binomial distribution to describe the behavior of a random variable that gives the number of classification errors in a sample of size n. DDM calculates for each instance i in the stream, the probability of misclassification (pi) and its standard deviation ; where . If the distribution of the samples is stationary, pi will decrease as sample size increases. A stationary process (on mean and variance) is one whose statistical properties do not change over time (Nason, 2010). If the error rate of the learning algorithm increases significantly, it suggests changes in the distribution of classes, causing the current constructed model to be inconsistent with current data, and thus providing the signal to update the model.
DDM calculates the values of pi and for each instance and when pi+si reaches its minimum value, it stores pmin and smin. Then, DDM checks two conditions to detect whether the system is in the warning or drifting level:
- The warning level is activated when pi+si≥ pmin +2smin. Beyond of this level, it stores the instances anticipating a possible change of context.
- The drift level is triggered when pi+si≥ pmin +3smin. In this level, DDM resets the variables (pmin and smin) and the induced model. Later a new model is learnt using the instances stored since the warning level was triggered.
DDM shows good performance for detecting gradual changes (if they are not very slow) and abrupt changes, but has difficulties detecting drift when the change is slowly gradual is possible that many samples are stored for a long time, before the drift level is activated and there is the risk of overflowing the sample storage space (Baena-Garcia, et al., 2006).




Performance evaluations of concept drift detection techniques presented in the literature generally consider the prequential error of the classifier and total number of changes detected by each method. In (Gama, Sebastiao, & Rodrigues, Issues in evaluation of stream learning algorithms) define the prequential error as the error obtained using each new instance arrival to test the model before it is used for training . This way the accuracy of the model can be incrementally updated.
Noise and outliers may increase false alarm rates in drift detection algorithms. Few evaluations regarding this problem are available in the literature. Sebastião and Gama (Sebastiao & Gama, 2009) present a study on Change Detection Methods. The experimental evaluation considers 5 different methods for concept drift detection (Statistical Process Control (Gama J. , Medas, Castillo, & Rodrigues, 2004), ADaptive WINdowing (Bifet & Gavalda, 2007), Fixed Cumulative Windows Model (Sebastiao & Gama) and Page Hinkley Test (Page) (Mouss, Mouss, Mouss, & Sefouhi)) and 4 fundamental aspects: to be able to detect and react to drift, not to exhibit miss detections, to be resiliant to false alarms in stationary environments, and to require few samples to detect a change. The experimental evaluation uses the dataset called SEA Concepts and calculates the error rate (computed using a naive-Bayes classifier), for the different methods. Assessing measures such as: false alarm rates, number of examples until a change is detected, and miss detections rates. This analysis is used to choose the more appropriated algorithms for detecting changes (Page Hinkley Test and the ADaptive WINdowing). The analysis also shows that for the chosen technique there is a trade-off between the rate of false alarms, the miss detections, and the delay until detection. Unlike (Sebastiao & Gama, 2009), our assessment considers the effect of noise on the evaluation of the various methods to determine their robustness in the presence of noisy data.
This section describes the evaluation of the different approaches to detect concept drift from data streams described above. These methods are implemented on top of the Massive On-line Analysis (MOA)framework ( The University of Waikato, 2015), a widely known framework for data mining evolving data streams written in Java.
The experiments focus on assessing the accuracy of the methods to correctly identify concept drift in the presence of noise. To test the different algorithms under the same conditions, we generated several synthetic datasets with RandomRBFGeneratorEvents and saved them to files. This way, the same dataset could be used as input to the different methods. RandomRBFGeneratorEvents is a generator based on the random Radial Basis Function that adds drift to samples in a stream (Bifet A. , RandomGeneratorDrift, 2012). The random radial basis function ( described in (Bifet, Holmes, Pfahringer, & Gavalda, 2009) ) generates a fixed number of random centroids. Each centroid has a random position, a class label, a standard deviation and a weight. The instances are generated by selecting a centroid at random. For this process, the weights of the centroids are taken into consideration, so centroids with larger weight are more likely to be chosen. The chosen centroid determines the class label of the instance. The r andom radial basis function gives rise to a normally distributed hypersphere of instances enclosing each centroid. Drift is added by moving the centroids at a constant rate.
For the evaluation, we use DriftDetectionMethodClassifier (Baena, 2012), a class for detect concept drift with a wrapper on a classifier. The chosen classifier is a Naive Bayes classifier and the Concept Drift Detection Technique can be any of the 4 methods (DDM, EDDM, GeometricMovingAverageDM and EWMAChartDM).
We configure the RandomRBFGeneratorDrift, so that it creates five centroids of which 2 have no movement (speedOption=0) and 3 do have. In a same execution, a cluster with movement can change its speed (speedOption may take 3 different values: 0.01/500, 0.001/500 and 0.1/500).
For the evaluation, we calculate 2 classification quality indices, accuracy (Rijsbergen, 1979) and Youden's J. The accuracy, see (19), is the ratio of true results among the total quantity of examples observed (Metz, October 1978). Youden's J, see (20), is a single statistic that corresponds to the best combination of sensitivity and specificity in the prediction and takes values between from -1 to 1 (Youden, 1950).

In the equations, TP is the number of true positives, FP the number of false positives, TN the number of true negatives and FN the number of false negatives. We identified that 23% is a good percentage to report a drift alert.
Figures 1 to 5 report the experimental results for noise level between 0 % and 20%.
Figure 1: Performance comparison for concept drift detection, noise level=0%.
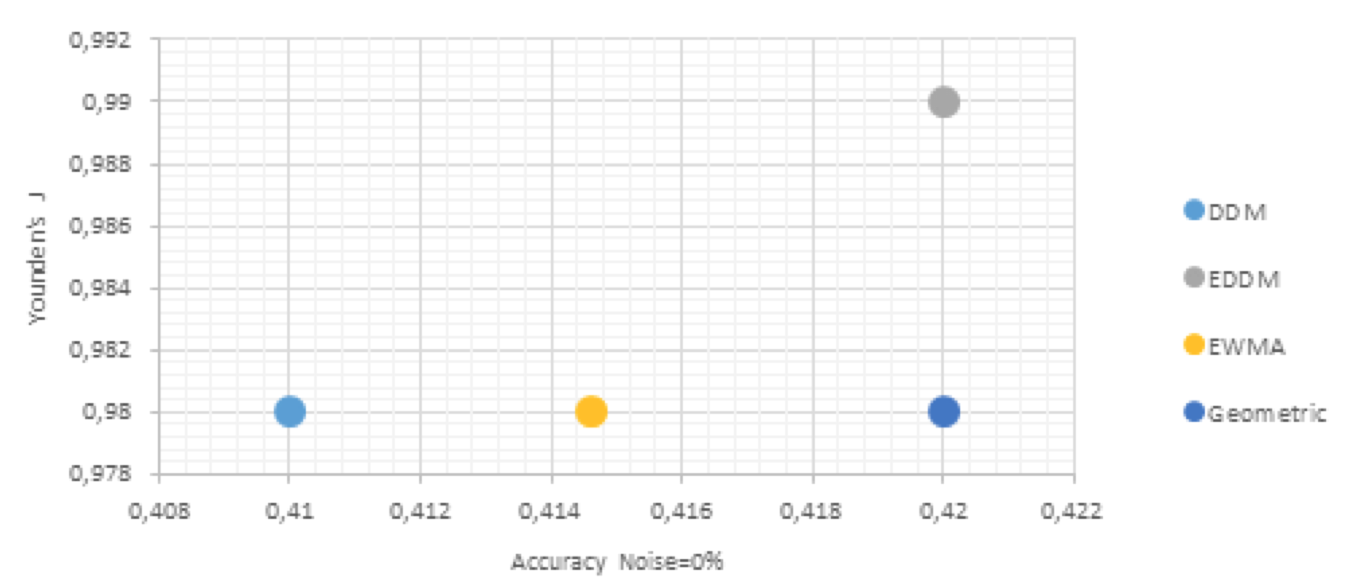
Source: Own image
Figure 2: Performance comparison for concept drift detection, noise level=5%.

Source: Own image
Figure 3: Performance comparison for concept drift detection, noise level=10%.
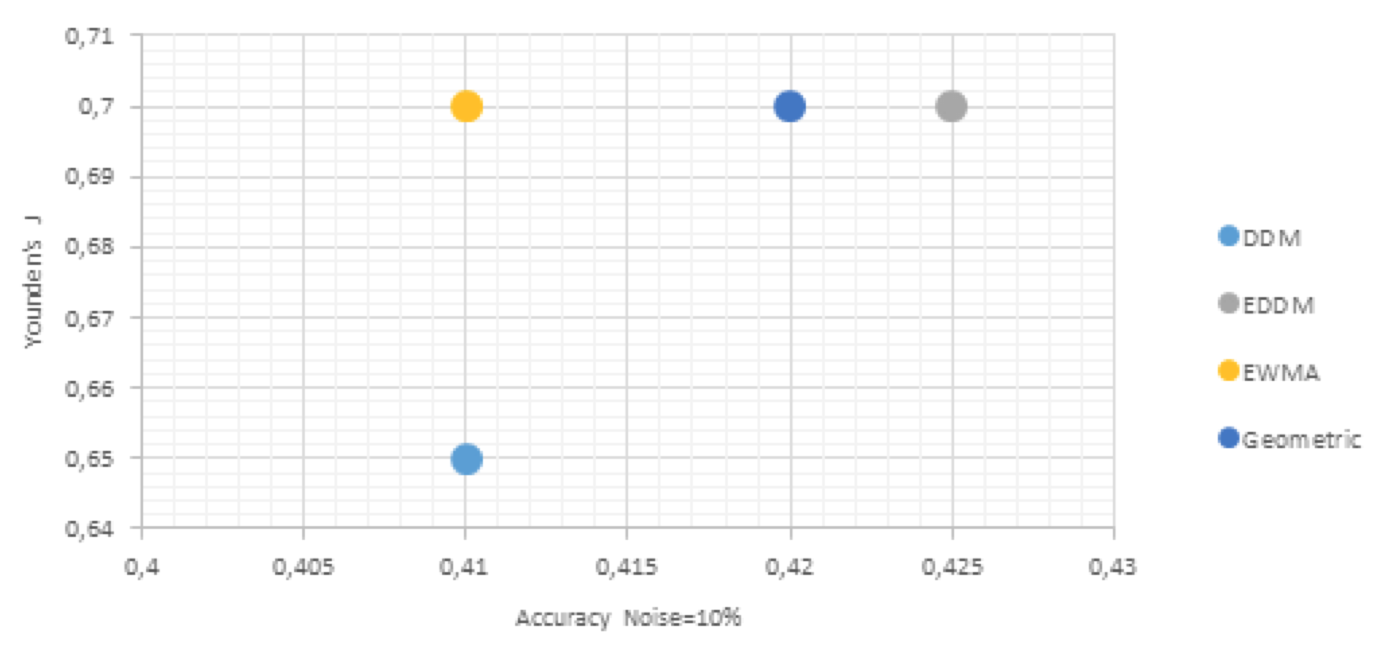
Source: Own image
Figure 4: Performance comparison for concept drift detection, noise level=15%.

Source: Own image
Figure 5: Performance comparison for concept drift detection, noise level=20%.
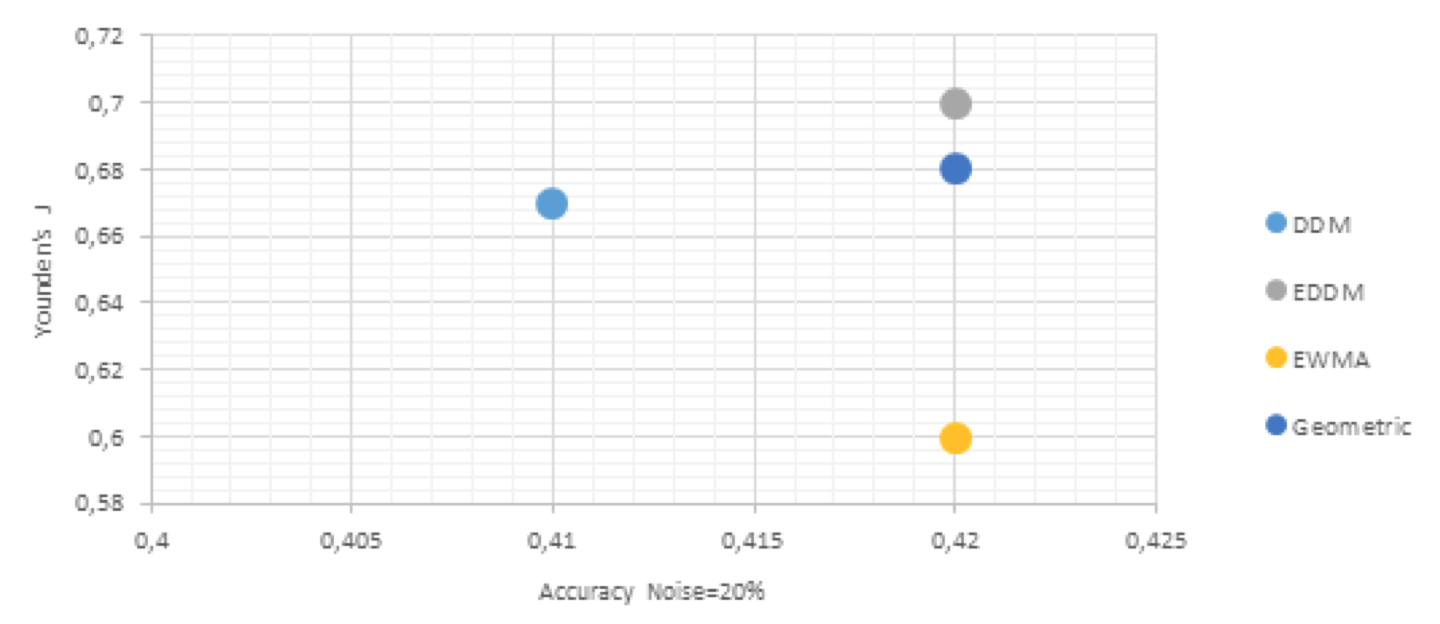
Source: Own image
From the observation of Figures 1-5, we can find that the classification accuracy and Youden’s J is always higher with EDDM, than with the 3 others methods of drift detection.
DriftDetectionMethodClassifier sends the result of the prediction obtained, with Naive Bayes classifier, to the drift detection approach. If it detects drift, a new model is induced by applying the classification algorithm in the samples stored since the warning level triggered.
In this paper, we evaluate 4 different algorithms for concept drift detection in the presence of noise. The experimental results show that the classification accuracy of Naive Bayes classifier is higher with EDDM for 5 levels of noise.
Directions for future work include exploring the 4 approaches in datasets with imbalance of classes and new emergent classes and implementing multivariate EWMA to report the occurrence of drift.
ANDRIENKO, G., ANDRIENKO, N., MLADENOV, M., MOCK, M., & POELITZ, C.Extracting Events from Spatial Time Series, (pp. 48-53), 2010.
BAENA, M. DriftDetectionMethodClassifier. From https://github.com/Waikato/moa/blob/master/moa/src/main/java/moa/classifiers/drift/DriftDetectionMethodClassifier.java, Retrieved april 5, 2016
BAENA-GARCIA, M., CAMPO-AVILA, J. D., FIDALGO, R., BIFET, A., GAVALDA, R., & MORALES-BUENO, R. Early drift detection method. Fourth International Workshop on Knowledge Discovery from Data Streams. 2006.
BASSEVILLE, M., & NIKIFOROV, I. V. Detection of Abrupt Changes. Upper Saddle River, NJ, USA: Prentice-Hall. Retrieved marzo 11, 2016, from ftp://ftp.irisa.fr/local/as/mb/k11.pdf, 2012.
BIFET, A. (2012). RandomGeneratorDrift. From http://www.cs.waikato.ac.nz/~abifet/MOA/API/_random_r_b_f_generator_drift_8java_source.html, Retrieved abril 5, 2016.
BIFET, A. (2012). RandomRBFGenerator. From http://www.cs.waikato.ac.nz/~abifet/MOA/API/classmoa_1_1streams_1_1generators_1_1_random_r_b_f_generator.html, Retrieved april 5, 2016.
BIFET, A., & GAVALDA, A. Learning from Time-Changing Data with Adaptive Windowing. Proceedings of the 7th SIAM International Conference on Data Mining. 2007.
BIFET, A., HOLMES, G., PFAHRINGER, B., & GAVALDA, R.. Improving Adaptive Bagging Methods for Evolving Data Streams. (Z.-H. Zhou, & T. Washio, Eds.) Advances in Machine Learning: First Asian Conference on Machine Learning, ACML 2009, Nanjing, China, November 2-4, 2009: Springer Berlin Heidelberg. Retrieved from http://dx.doi.org/10.1007/978-3-642-05224-8_4, 2009.
BRZEZIŃSKI, D. (2010). Mining data streams with concept drit. From http://www.cs.put.poznan.pl/dbrzezinski/publications/ConceptDrift.pdf. Retrieved december 02, 2015.
CHANDOLA, V., BANERJEE, A., & KUMAR, V. Anomaly Detection: A Survey. ACM Computing Surveys (CSUR), 41(3), 15:1-15:58. Retrieved from http://doi.acm.org/10.1145/1541880.1541882, 2009.
CHAUDHRY, N., SHOW, K., & ABDELGUERFI, M. Stream data management. Advances in Database system . Vol. 30. Springer, 2005.
DEL CASTILLO, E. Some properties of ewma feedback quality adjustment schemes for drifting disturbances. Journal of Quality Technology, 33(2), 2001.
DONGRE, P. B., & MALIK, L. G. Stream Data Classification and Adapting to Gradual Concept Drift. International Journal of Advance Research in Computer Science and Management Studies, 2 (3). 2014.
DONGRE, P., & MALIK, L. A review on real time data stream classification and adapting to various concept drift scenarios. Advance Computing Conference (IACC), IEEE International , (pp. 533-537), 2014.
FANG CHU, A. Doctoral Dissertation Mining Techniques for Data Streams and Sequences. Retrieved from http://wis.cs.ucla.edu/old_wis/theses/chu_thesis.pdf, 2005.
GAMA, J. Knowledge Discovery from Data Streams. From http://www.liaad.up.pt/area/jgama/DataStreamsCRC.pdf. Retrieved marzo 11, 2016.
GAMA, J., MEDAS, P., CASTILLO, G., & RODRIGUES, P. Learning with drift detection. Lecture Notes in Computer Science 3171, 2004.
GAMA, J., MEDAS, P., CASTILLO, G., & RODRIGUES, P. Learning with Drift Detection. Advances in Artificial Intelligence - SBIA 2004, Vol.3171 of Lecture Notes in Computer Science(Springer Verlag), 286-295, 2004.
GAMA, J., SEBASTIAO, R., & RODRIGUES, P.. On evaluating stream learning algorithms. Machine Learning, 90(3) , 317–346, 2013.
GAMA, J., SEBASTIAO, R., & RODRIGUES, P. P. Issues in evaluation of stream learning algorithms. Proceedings of KDD, 329-338.
GAMA, J., ZLIOBAITE, I., BIFET, A., PECHENIZKIY, M., & BOUCHACHIA, A. A Survey on Concept Drift Adaptation. (ACM Computing Surveys, Vol. 1, No. 1, Article 1, Publication date: January 2013.
HOENS, T., POLIKAR, R., & CHAWLA, N. Learning from streaming data with concept drift and imbalance: an overview. Progress in Artificial Intelligence, 1(1), 89-101. Retrieved from http://dx.doi.org/10.1007/s13748-011-0008-0, 2012.
JIAWEI, H., & KAMBER, M. Data Mining: Concepts and Techniques. Elsevier. 2011.
KELLY, M. G., HAND, D. J., ADAMS, & M., N. The impact of changing populations on classifier performance. KDD '99 Proceedings of the fifth ACM SIGKDD international conference on Knowledge discovery and data mining, 367–371. 1999
LE, T., STAHL, F., GOMES, J. B., MEDHAT GABER, M., & DI FATTA, G.. Computationally Efficient Rule-Based Classification for Continuous Streaming Data. Springer International Publishing Research and Development. Switzerland, 2014.
METZ, C. Basic principles of ROC analysis. Semin Nucl Med. , 8 (4): 283–98, October 1978
MINKU, L., & YAO, X. DDD: A New Ensemble Approach for Dealing with Concept Drift. Knowledge and Data Engineering, IEEE Transactions on, 24(4), 619-633, 2012.
MOUSS, H., MOUSS, D., MOUSS, N., & SEFOUHI, L. Test of Page-Hinkley, an Approach for Fault Detection in an Agro-Alimentary Production System. Proceedings of the 5th Asian Control Conference. Vol.2, pages: 815-818, 2004.
NARASIMHAMURTHY, A., & KUNCHEVA, L. I. A Framework for Generating Data to Simulate Changing Environments. AIAP'07 Proceedings of the 25th conference on Proceedings of the 25th IASTED International Multi-Conference: artificial intelligence and applications (pp. 384-389). Anaheim, CA, USA: ACTA Press. Retrieved from http://dl.acm.org/citation.cfm?id=1295303.1295369, 2007.
NASON, G. P. Stationary and non-stationary time series. From http://www.cas.usf.edu/~cconnor/geolsoc/html/chapter11.pdf, 2010. Retrieved marzo 14, 2016
OZA, N., & RUSSELL, S. Experimental Comparisons of Online and Batch Versions of Bagging and Boosting. ACM SIGKDD Int’l Conf. Knowledge Discovery and Data Mining, 359-364. 2001
PAGE, E. S. Continuous Inspection Schemes. Biometrika, 41:100-115, 1954.
RIJSBERGEN, C. Information Retrieval. Retrieved from http://www.dcs.gla.ac.uk/Keith/Preface.html, 1979.
ROBERTS, S. W. Control chart tests based on geometric moving average. Technometrics, 42(1):97. 2000.
ROSS, G. J., ADAMS, N. M., TASOULIS, D. K., & HAND, D. J. Exponentially Weighted Moving Average Charts for Detecting Concept Drift. Pattern Recognition Letters, 33(2) 191-198, 2012.
SADHUKHA. (2003). Change detection algorithms. From http://www.research.rutgers.edu/~sadhukha/file2.pdf, Retrieved marzo 14, 2016.
SEBASTIAO, R., & GAMA, J. (2009). A Study on Change Detection Methods. 4th Portuguese Conf. on Artificial Intelligence, 353-364. Retrieved marzo 09, 2016, from epia2009.web.ua.pt/onlineEdition/353.pdf
SEBASTIAO, R., & GAMA, J. Monitoring Incremental Histogram Distribution for Change Detection in Data Streams. Lecture Notes in Computer Science (LNCS).
THE UNIVERSITY OF WAIKATO. MOA. Retrieved december 04, 2015, from http://moa.cms.waikato.ac.nz/details/, 2015.
WANG, H., YU, P., & HAN, J. Mining Concept-Drifting Data Streams. In O. Maimon, & L. Rokach (Eds.), Data Mining and Knowledge Discovery Handbook (pp. 789-802). Springer US. Retrieved from http://dx.doi.org/10.1007/978-0-387-09823-4_40. 2010
WANG, H., YU, P., & HAN, J. Mining Concept-Drifting Data Streams. In O. Maimon, & L. Rokach (Eds.), Data Mining and Knowledge Discovery Handbook (pp. 789-802). Springer US. Retrieved from http://dx.doi.org/10.1007/978-0-387-09823-4_40. 2010
WIDMER, G., & KUBAT, M. Learning in the Presence of Concept Drift and Hidden Contexts. Journal Machine Learning archive, Volume 23 Issue 1, (pp. 69-101). USA, 1996
YEH, A., MCGRATH, R., SEMBOWER, M., & SHEN, Q. EWMA control charts for monitoring high-yield processes based on non-transformed observations. International Journal of Production Research 46 (20), 5679-5699. 2008
YOUDEN, W. J. Index for rating diagnostic tests. Cancer, 3(1), 32-35. Retrieved from http://dx.doi.org/10.1002/1097-0142(1950)3:1<32::AID-CNCR2820030106>3.0.CO;2-3
1. PhD candidate in Engineering. Computer Engineering Dept., Universidad del Quindío, UQ. Armenia, (Colombia), Email: sjaramillo@uniquindio.edu.co
2. PhD in Computer Science. Engineering Dept. Universidad Pontificia Bolivariana, UPB. Medellín, (Colombia), Email: jorge.londono@upb.edu.co
3. PhD candidate in Engineering. Computer Engineering Dept., Universidad del Quindío, UQ, Armenia, (Colombia), Email: sergio_cardona@uniquindio.edu.co