ISSN 0798 1015

Vol. 38 (Nº 33) Año 2017. Pág. 25

Properties of Complex Dispersion and Standard Deviation

Propiedades de Dispersión Compleja y Desviación Estándar

Sergey Gennadievich SVETUNKOV 1; Amina Fanisovna CHANYSHEVA 2

Received: 30/05/2017 • Approved: 15/06/2017

Content

1. Introduction

2. Method

3. Results

4. Discussion

5. Conclusion

Acknowledgements

References

1. Introduction

Econometrics today is one of the sections of economic-mathematical modeling which is highly developed and demanded by economic practice. The problems of description, explanation and forecasting of diverse tendencies of social and economic dynamics or interrelations between factors continuously arise before the economist at all stages of his/her activity – from macro- to microlevel. And though today the number of the econometric models used in practice is quite big, it is hard to describe all types of economic processes using them. Therefore the problem of expansion of the models range that can be used in econometrics remains relevant.

Functions of complex variables solve this problem as they represent the tool which describes the relationship between economic variables in another way than the real variables models do. Various functions of complex variables with rare exception allow the economist to model such nonlinear interrelations which have no analogues in real variables econometrics or such analogues are too complicated for practical use. Thus, using the complex variables models significantly expands the instrumental base of the econometric researches (Svetunkov, 2012, Chanysheva, 2009 & 2013).

In mathematical statistics there are some practices concerning statistics of random complex variable that should be used to the extent that they are suitable for the tasks. Judging by scientific literature available at our disposal, interest to statistical processing of observations for variation of a complex variable arose in the 50-60-ies of the XX century (Wooding ,1956; Arens, 1957; Reed, 1962; Goodman, 1963; Feller, 1966; Rukhin, 1967). Further some other properties of statistics of a random variable were also found out, but these developments are scarce and insufficient for the purposes of econometrics of a complex variable.

2. Method

First of all, some basic information on the statistical characteristics of the complex random variable will be introduced.

2.1. Population mean

Firstly, we will give the standard concept of statistics of a complex variable — its population mean.

Population mean of a complex random variable

is the complex number:

 (1)

Since any complex number can be presented as a couple of real numbers, mathematical statistics considers that complex representation of stochastic functions is no more than a mathematical form of their display convenient for the analysis which can be always transferred to a form of material functions. For this reason, the functions of dispersion, correlation and covariance in mathematical statistics are represented as unambiguous and nonrandom material characteristics of casual processes and functions, irrespective of a form of their mathematical representation.

2.2. Dispersion

Dispersion of a complex random variable represents (Ventzel, 2010, p. 460): "population mean of a square of the absolute value of the corresponding centered value":

(2)

where

(3)

, (4)

The key phrase here is the phrase "absolute value" as the absolute value of complex variable is a real value. Dispersion of a complex random variable, considering (2), is equal to the sum of dispersions of its real and imaginary parts.

The important characteristic used in mathematical statistics is the correlation moment. According to the definition used in mathematical statistics, the correlation moment is a real number. For that reason, the population mean of product of two random complex numbers:

could not be considered as the correlation moment because the product of two complex variables will be a complex number.

In addition, the correlation moment of two equal random variables in mathematical statistics of real variables is equal to dispersion, and it could not be derived from the above formula. Therefore in mathematical statistics the correlation moment of a complex random variable is considered as a population mean of product of one variable to conjugate value of another one:

, (5)

Carrying out multiplication and grouping the summands, we get:

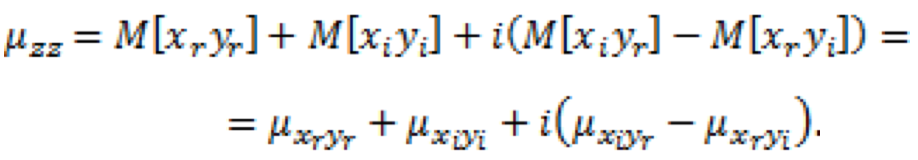, (6)

In the case when z1=z2=z, the last item in (6) becomes equal to zero and the correlation moment is equal to dispersion (2), that was important to get for a perfect analogy to statistics of real random variables.

Basing on these ideas of a random complex variable, it is possible to develop them further and to apply a least-squares method to assess interrelation between two random complex variables (Tavares, 2007).

We will show a fallibility of the assumption that variability measures of complex variables are real values.

We will consider a couple of random complex variables changing in time: (yrt+iyit) и (xrt+ixit). In economy it can be, for example, such couple: price of oil unit and gas unit, or couple: the dollar-ruble and euro-ruble exchange rate, or any other couple representing different aspects of the same phenomenon. To avoid bulky calculations and records, we will use the values of complex variables centered relatively to their arithmetical means.

2.3. The coefficient of pair correlation

It is known that the coefficient of pair correlation for the real variables can be found by means of the correlation moment as follows (Kremer and Putko, 2002; Eliseeva, 2003):

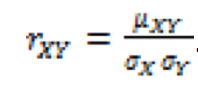, (7)

If we substitute random complex variables and their selective values of the correlation moment and standard deviation instead of random real variables in this formula, we will get a formula for complex coefficient of pair correlation.

With the use of the variables centered relatively to their arithmetical means, it will look like (Svetunkov, 2011, p. 8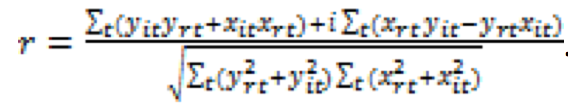8):

, (8)

It is easy to find out that the coefficient (8) is a complex value that obviously contradicts the aprioristic desire to have real values as the measures characterizing complex random variables.

In addition, as we know, the coefficient of pair correlation is defined as the geometric mean of the regressions coefficients of y on x and x on y (Slutsky, 2010):

, (9)

Operating with that variant of least-squares method which follows from the assumption that the dispersion of a complex variable (2) is a real number, and substituting estimates of this least-squares method in (9), we will get such formula for complex coefficient of pair correlation (Svetunkov, 2011, p. 104):

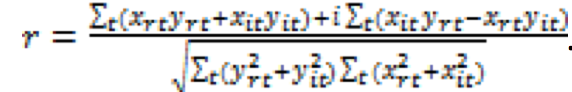, (10)

The denominators of formulas (8) and (10) coincide but their numerators are fundamentally different from each other. We got the contradictory variant and it means that the a priori assumption that all main indicators characterizing casual process (dispersion, correlation moment, covariance, etc.) are real values, is incorrect.

3. Results

3.1 Complex dispersion

In the paper (Svetunkov, 2011) it is proved that all statistical characteristics of complex random variables must be complex. This statement allowed to establish the foundation of the new research field– econometrics of complex variables. But the paper does not consider the properties of one of the fundamental characteristics, namely – complex dispersion. We will amend this flaw.

We will introduce a new concept — complex dispersion of a complex random variable. It will be the population mean of a square of the corresponding centered value (Svetunkov, 2012, p. 102):

, (11)

where

, (12)

, (13)

Using this new concept of complex dispersion, it is easy to get consistent result if we deduce a formula of complex coefficient of pair correlation through (7) and (9).

Really, the complex correlation moment in this case will look like:

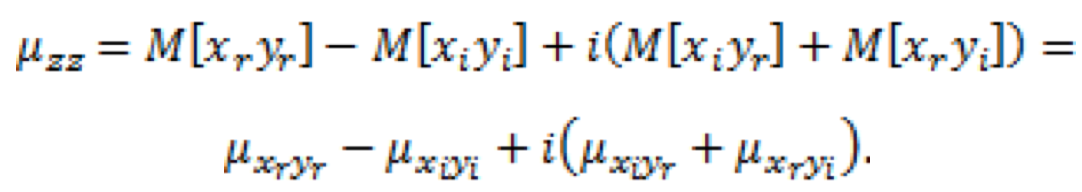, (14)

Substituting this value in (7), we will get for the centered variables:

, (15)

It is easy to notice that formula (15) doesn't coincide with (8), nor with (9).

We will find now complex coefficient of pair correlation through the geometrical mean of the regression coefficients (9) if these coefficients are found by means of complex least-squares method with the use of complex dispersion (Svetunkov, 2012, p. 112):

, (16)

Apparently, the same formula of complex coefficient of pair correlation as in case of its calculation through the correlation moment (15) is got. So, consistent result is got, and it means that it is necessary to use complex dispersion in statistics of complex random variables instead of its real analog as it is approved today. We will consider now the properties of complex dispersion in more detail.

It follows from (11) that complex dispersion can be complex number, or real negative value, or maybe imaginary value — a variety of its values corresponds to variety of properties of a complex variable. Such possible values of complex dispersion are quite normal — since in Minkowski's geometry, for example, distances can be negative or even imaginary (Ilyin, 2014; Thompson, 1996), there is nothing strange in the result that we got — it should be like this for complex variables if we consider them in corpore.

The real part of dispersion of a complex random variable (11) characterizes the measure of difference of dispersion of real part of the complex random variable from dispersion of imaginary part of the complex random variable.

If these dispersions are equal to each other, the real part of complex dispersion (11) will be equal to zero.

If dispersion of real part of a random variable is more than dispersion of imaginary part of this variable, the real part of complex dispersion will have positive sign. In the other case it will have negative sign.

Since the correlation moment of two independent variables is equal to zero, the meaning of the imaginary part of complex dispersion is clear. The imaginary part of complex dispersion will characterize the measure of independence of the real and imaginary parts of a complex variable from each other. If they are independent, the imaginary part of complex dispersion will be equal to zero. However, it will also be equal to zero in certain cases which we will consider below on concrete examples.

In order to identify patterns in the behavior of complex dispersion, a number of conditional examples were analyzed. As the values of the complex variable yr+iyi, two time series of indicators yr and yi were used. Different variants of relation between yr and yi were thus considered - both functional and correlation. To identify the existence of linear dependence between indicators and the measure of influence of this dependence on complex dispersion, the usual coefficient of correlation r was used.

We will designate for convenience the real part of complex dispersion as dr and the imaginary part as di:

(17)

The calculations led to the following results.

3.2. Properties of complex dispersion

The imaginary part of complex dispersion of di is close to zero in the cases:

1) there is no linear functional relation between the real and imaginary parts of complex value. The correlation coefficient is thus equal or very close to zero.

In Figures 1, 2 and 3 there are examples of some relations of variables on the complex plane which has the imaginary part of complex dispersion close to zero. The linear trend describing these relations is also represented (it is almost parallel to abscissa axis).. The abscissa axis and the axis of ordinates show the values of yr and yi respectively.

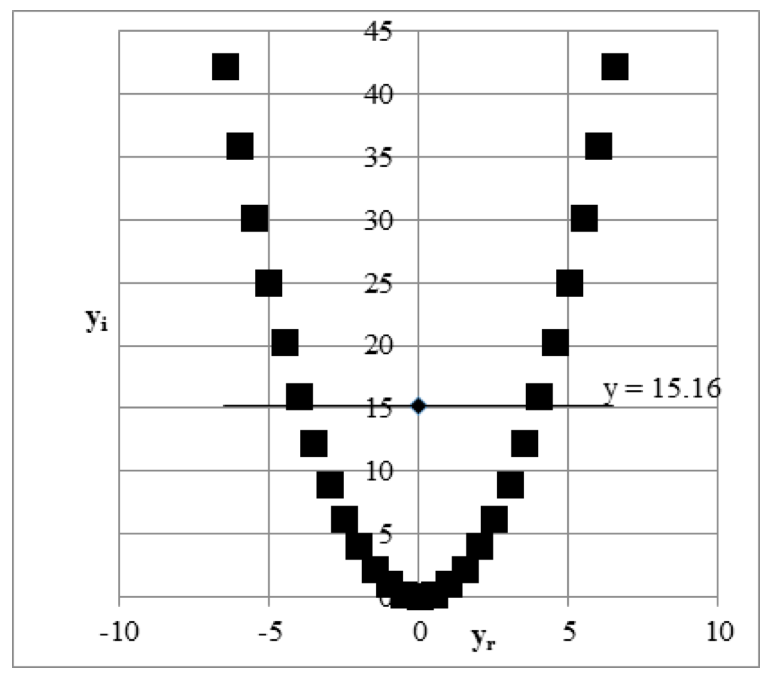
Figure 1. Parabolic relation between yr and yi, r=0.
D= –168.09+i0,00= –168.09

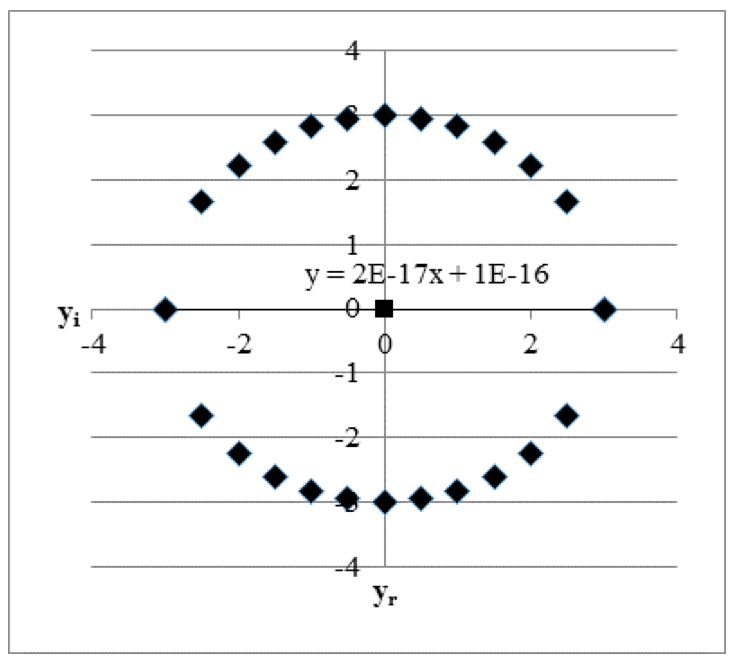
Figure 2. Relation of yi on yr is described by the circle equation, r=0.
D= –2.00+i0.00= –2

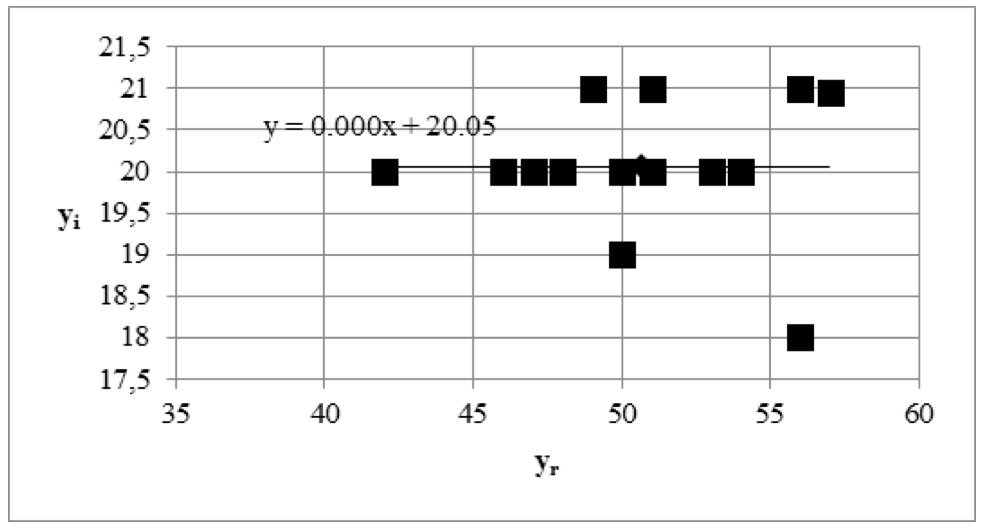
Figure 3. Statistical relation between yi and yr, r=0.0007.
D= 15.1+i0.00425

2) there is a linear functional relation between the real and imaginary parts of the complex variable yr+iyi, and the regression function is parallel to one of coordinate axes (Figure 4). It is impossible to calculate the correlation coefficient r in this case since there is a division by zero. Covariance between the real and imaginary parts of a complex variable is thus equal to zero that is obvious since the imaginary part di represents the doubled covariance between yr and yi (see formula 11).

Figure 4. Linear functional relation.

In case the imaginary part of complex dispersion di is other than zero, we will be interested in two characteristics — the sign and the value of di.

1. The sign of an imaginary component is positive if the tendency between the factors considered on the complex plane has a positive angle of inclination, and is negative otherwise (Figures 5, 6). This can be also confirmed by the value of pair correlation coefficient r calculated for two datasets of yr and yi. The sign of imaginary part of complex dispersion di corresponds to the sign of correlation coefficient r for any kind of relations between yr and yi.

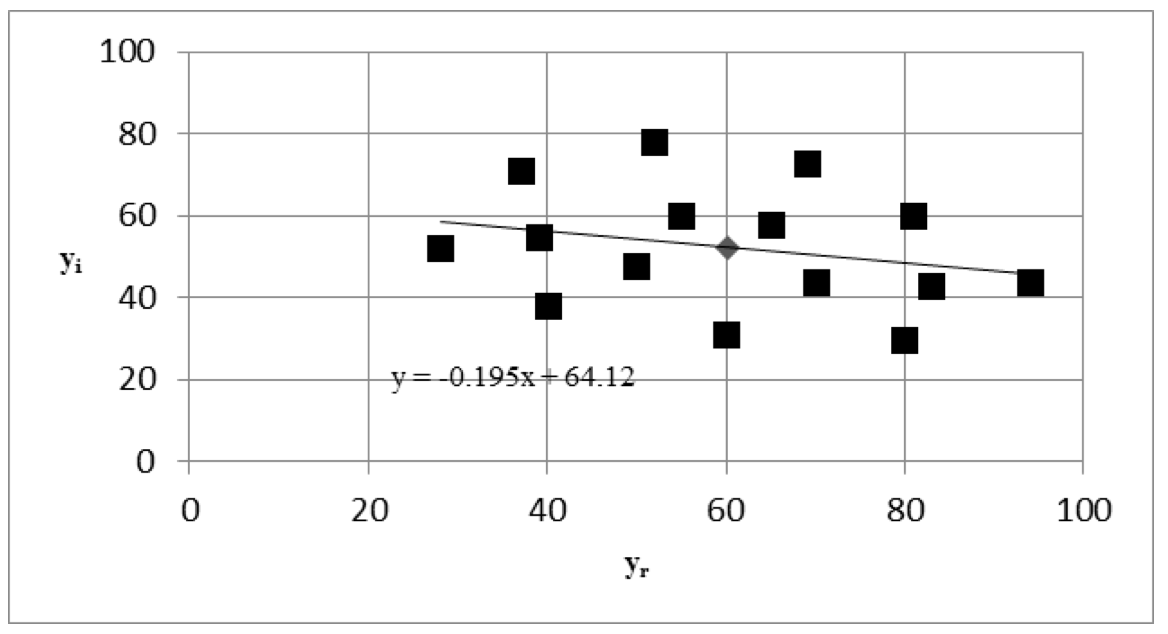
Figure 5. Statistical relation between yi and yr, r = -0.2609.
D=154.61 – i138.8

Figure 6. Statistical relation between yi от yr, r = 0.4028.
D=9.3+i8.04

2. Since the value di represents the linear modification of covariance between yr and yi, and covariance is the average of products of deviations for each couple of points of the analyzed data:

, (18)

the value di will depend on basic data scattering around its’ mean. While the scatter of values of yr and yi around its’ mean increase the value of di also increases.

The real part of complex dispersion becomes equal to zero for the case of linear functional relation between yr and yi when the dispersions of both values are equal. There is a special case when the regression function on the complex plane represents a straight line with inclination angle of or .

In case the real part of complex dispersion dr differs from zero, we consider again two characteristics — the sign and the value of dr.

1. The sign of dr is determined by values of dispersions of yr and yi – if the dispersion of yr is more that the dispersion of yi, dr will have positive values, and vice versa. That is, the sign of the real part of complex dispersion shows which indicator (yr or yi) has bigger scatter of values around its’ mean value. For a special case of linear functional relation between yr and yi, the following regularity was revealed: dr is positive if the inclination angle of straight line  belongs to the interval , and is negative if

2. The value of indicator dr is obviously determined by the measure of distinction of dispersions of yr and yi. The greater this distinction is, the greater the absolute value of an indicator dr will be.

So, the meaning of the components of complex dispersion – its real and imaginary parts — is clear. It is also clear that the use of the new characteristic — complex dispersion – along with dispersion of a complex variable (2), significantly expands the conception of the researcher about the variation of a complex random variable.

3.3. The standard deviation

The standard deviation is one more widespread characteristic in mathematical statistics describing the value of a variation of characteristic in population. It can be considered as the square root of dispersion (Eliseeva, 2002):

. (19)

In complex-valued economy we will consider the similar indicator S=sr+isi that is equal to the square root of complex dispersion:

, (20)

where S is the complex standard deviation.

Calculation of complex standard deviation, in fact, means raising complex dispersion to a power ½:

, (21)

whereRD is the complex dispersion module, ,

θ is the polar angle of complex dispersion,

It means that the module of complex dispersion decreases when calculating standard deviation and the polar angle characterizing the ratio of the real and imaginary parts is halved.

The sign si corresponds to the sign di, i.e. indicates increase (decrease) of the trend line. In case when complex dispersion has the real part equal to zero and the imaginary part not equal to zero, complex standard deviation, as appears from (21), will have equal absolute values of the real and imaginary parts. For example, if dispersion equals D=0+i16, complex standard deviation will be S=4+i4, characterizing the symmetry of dispersions of the real and imaginary parts of a complex variable.

4. Discussion

We will show the above on a simple example analyzing a dataset of daily prices for Brent crude oil and gas. The general trend of these values becomes apparent in long-term dynamics, but in a short-term perspective we can observe fluctuations around some constant.

Data which can be used for the analysis of properties of complex dispersion of this dataset are provided in Table 1. One thousand cubic meters of natural gas contains 35.8 million BTU.

The world price for oil and the world price for gas reflect the demand of world economy for energy sources. Evaluating forecasts for oil is very important because the world prices for oil and gas largely affect the Russian economy, since about 40% of the Russian budget consists of oil and gas revenues. The price for gas is calculated from the price for oil and is directly dependent on it (Kruk and Nikulina, 2016; Nikulina and Kruk, 2016).

Table 1. Statistical data for oil and gas prices

Since oil and gas are the most widespread energy sources reflecting global trends, they can be represented as a complex variable (reduced to dimensionless form):

. (22)

This complex variable changes its values around certain quantity; the assessment for that quantity can be the arithmetic mean:

. (23)

Fluctuations of real values relatively to this arithmetic mean are reflected by complex selective dispersion:

. (24)

According to the obtained values of complex dispersion it is possible at once to draw conclusions on a studied dataset of a complex random variable.

First of all, the real part of complex dispersion is positive and rather big. It testifies that dispersion of the oil price is higher than gas price dispersion. If we consider that the oil price in Table 1 is measured by hundreds, and the gas price by units, this conclusion is clear. Therefore, for more careful analysis it would be necessary to bring these two variables to one scale, for example, in relation to the initial values.

The second conclusion which can be made studying the complex dispersion is that there is a close linear interrelation between the real and imaginary parts of it — the imaginary part of complex dispersion in comparison with its real part is rather small and close to zero.

We will consider now an assessment of possible values of a complex random variable (22). For this purpose, we need to calculate the standard deviation which will be a complex value basing on the value of complex dispersion. Really, the square root of complex selective dispersion (24) gives such value of standard deviation:

. (25)

We do not pose the problem of getting certain practical conclusions and recommendations, but we review this example as an argument in favor of using the complex dispersion and its characteristics. Therefore we will use in this case Student’s t-statistics for 0.8 percentage probability which equals 1.363:

. (26)

Then the actual values of a complex variable will lie in the limits:

or

. (27)

It is obvious that with increase in number of observations on this complex variable dispersion will decrease, and confidence interval will contract.

Thus, it is possible to draw an unambiguous conclusion — in econometrics of complex variables all characteristics and measures of variability have to be complex, dispersion first of all.

5. Conclusion

In conclusion it should be said that complex-valued economics is a new and perspective field of economics. Construction of economic models both in macro- and microeconomics is always relevant and should be done with the aim of evaluating any kind of forecasts. As the authors show in their works, using of the complex variables in such models can substantially increase the quality of such forecasts. Future research can be devoted to the construction of non-linear econometric models with the use of complex variables and the evaluation of the complex statistical characteristics for them. Obviously, such models should be applied to the real economic processes.

Acknowledgements

Work is performed with financial support of the Russian Fund for Fundamental Researches, grant No. 13-06-00316 " Development of complex analysis of the efficiency of mineral resources of Russia"

References

Arens, R. (1957).Complex Processes for Envelopes of Normal Noise. IRE Trans. Inform. Theory, IT-3, 204-207.

Chanysheva, A.F. (2009). Confidence estimations of economic indicators forecasts using complex variables regressions. Proceedings of the St. Petersburg University of Economics and Finance, 4 (60), 162-164.

Chanysheva, A.F. (2013). Confidence Ranges in Complex Variables Econometrics. Business Inform, 8, 110–116.

Eliseeva, I.I. (2003). Econometrics: a Textbook. Moscow: Finance and Statistics.

Feller, W. (1966). An Introduction to Probability Theory and its Applications. (Vol. II). New York: Wiley.

Goodman, N.R. (1963).Statistical Analysis Based on a Certain Multivariate Complex Gaussian Distribution. Ann. Math. Statist., 34, 152-176.

Ilyin, V.A. (2014). Linear Algebra and Analytic Geometry: a Textbook. (3rd ed.). Rev., Moscow: Prospect.

Kruk, M.N. & Nikulina, A.Y., (2016).Economic Estimation of Project Risks when Exploring Sea Gas and Oil Deposits in the Russian Arctic. International Journal of Economics and Financial Issues, 2(6), 138 - 150.

Kremer, N.SH. & Putko, B.A., (2002). Econometrics: a Textbook. Moscow: Uniti-Dana.

Nikulina, A.Y. & Kruk, M.N., (2016). Impact of Sanctions of European Union and Unites States of America on the Development of Russian Oil and Gaz Complex. International Journal of Economics and Financial Issues, 4 (6), 1379 - 1382.

Nikulina, A.Y. & Kruk, M.N., (2016). Organizational and Economic Mechanism of Oil and Gas Projects in the Russian Arctic Shelf. Journal of Internet Banking and Commerce, 6 (21), 1 - 12.

Reed, I.S. (1962).On a Moment Theorem for Complex Gaussian Processes. IRE Trans. Inform. Theory, IT-8, 194-195.

Ruhin, A. L. (1967).The Complex Normal Law and the Admissibility Mean as an Estimator of the Shift Parameter. Theory of Probability and its Applications, 12(4), 762-764.

Slutsky, E.E. (2010). Correlation Theory and Elements of the Doctrine of Distribution Curves. Slutsky E.E. Economic and statistical work: Selected. Moscow: Penguin Books, pp. 1152.

Svetunkov, S. G. (2011). Fundamentals of Complex-Valued Economy. St.-Petersburg: IP Vasilkina M.N.

Svetunkov, S. G.(2012). Complex-Valued Modeling in Economics and Finance. New York: Springer Science + Business Media, pp. 318.

Tavares, G. N., and Tavares, L. M. (2007).On the Statistics of the Sum of Squared Complex Gaussian Random Variables. IEEE Transactions on Communications, 55(10), pp. 1857-1862.

Thompson, A.C. (1996). Minkowski Geometry. Cambridge: Cambridge University Press, pp. 364.

Ventzel, E.S. (2010). Probability Theory: a Textbook. Moscow: KNORUS.

Wooding, R. A. (1956).The Multivariate Distribution of Complex Normal Variables. Biometrika, 43, 212-215.

1. National Research University Higher School of Economics, 194100, Saint-Petersburg, Kantemirovskaya Street, 3 building 1, litera A

2. Saint-Petersburg Mining University, 199106, Saint-Petersburg, Vasilevsky island, line 21, 2; Email: aminusha@yandex.ru