ISSN 0798 1015

Vol. 38 (Nº 29) Año 2017. Pág. 30

Reprogramación de producción en cadenas de suministro colaborativas: Una revisión de la literatura

Reactive scheduling in collaborative supply chain: A literature review

ACEVEDO-CHEDID, Jaime 1; SALAS-NAVARRO, Katherinne 2; OSPINA-MATEUS, Holman 3; SANTANDER-MERCADO, Alcides 4

Recibido: 16/01/2017 • Aprobado: 21/02/2017

Contenido

1. Introducción

2. Metodología

3. Clasificación de los problemas de reprogramación de la producción en cadenas de suministro colaborativas

4. Conclusiones

Referencias bibliográficas

1. Introducción

Establecer una cadena de suministro implica enmarcar relaciones de algún grado de integración operacional que conllevan a que los eslabones estén comunicados, a fin de poder establecer un programa de producción local, que debe determinar la mejor asignación y ordenamiento en el tiempo de los recursos disponibles y/o compartidos, considerando las restricciones del sistema y minimizando determinados objetivos de fabricación, sin sacrificar niveles de servicio al cliente (Rodammer et al. 1988). Dichas asignaciones y secuencias deben obedecer a un conjunto de reglas o restricciones, establecidas en un esquema que sirva de referente para el eslabón en cuestión (Baudin, 1990). Así mismo y teniendo en cuenta la variabilidad intrínseca de un mundo globalizado, que se evidencia en las perturbaciones y modificaciones de las condiciones, parámetros y restricciones iniciales del programa de producción (Díaz y Bejarano, 2009) -por ejemplo llegada de nuevas órdenes, averías de máquina, cambios es las especificaciones de los productos, mantenimientos de máquinas, alistamientos etc.- la gestión de la cadena de suministro requiere que los programadores y los sistemas de programación local reaccionen haciendo una reprogramación de lo planeado (Dorn et al.1995). En la actualidad las empresas compiten en un mercado global con múltiples desafíos de apertura de nuevos mercados, clientes, productos, servicios, entre otros. Los cuales hacen necesario la generación permanente de nuevas estrategias que permitan adaptarse a las condiciones cambiantes del entorno y sobrevivir un mercado cada vez más competitivo (Salas et al., 2016).

La programación y reprogramación de producción en la cadena de suministro es uno de los procesos que requieren mayor eficiencia si se desea obtener un sistema altamente sincronizado y coordinado (Rodammer et al. 1988). La reprogramación de producción en una cadena de suministro es el proceso de actualización del programa de producción existente en respuesta a unas alteraciones determinadas (Vieira et al. 2003; Song, 2001; Morton y Pentico, 1993), debe enfocarse como un proceso dinámico que debe responder rápidamente a las alteraciones de las condiciones de programación y por ende cobra un papel de importancia si se desean desarrollar operaciones exitosas en el sistema de fabricación (Bean et al. 1991).

Ante la necesidad, que se les presenta a las cadenas de suministro de la pequeña y mediana industria de ofrecer conjuntamente óptimos niveles de servicio, se hace necesario la implementación de eficientes sistemas de distribución de los productos hasta los clientes finales, la entrega de la mayor cantidad de órdenes a los clientes en las fechas requeridas y minimización de los costos (Bustamante, 2009); y ante la ausencia de coordinación y sincronización entre los eslabones de la cadena de suministro, se ha convertido en prioridad establecer políticas y metodologías que permitan integrar y unir esfuerzos para obtener una mayor utilización de las capacidades conjuntas (Croom et al. 2000; Agnetis et al. 2001; Felix et al. 2006), entre otros beneficios y como resultado lograr una red colaborativa en la cadena de suministro (Herrmann, 2001). Las estrategias de colaboración en cadenas de suministro surgen como respuesta para aprovechar diversas oportunidades de mejora que presenta la gestión de las cadenas de suministro (Kogut, 1988) y a fin de incrementar la eficiencia de los procesos a través la reducción de costes, mejoría de la calidad y agilización de las operaciones. La orientación hacia la integración y colaboración, supone eliminar barreras no sólo entre los procesos de negocios de la empresa sino entre las empresas para simplificar las actividades, hacerlas más eficientes y eliminar las tareas duplicadas (Hammer, 2001).

Las redes colaborativas pueden definirse como acuerdos por medio del cual dos o más empresas autónomas trabajan conjuntamente para planear y ejecutar operaciones de la cadena de suministro a la que pertenecen (Arshinder et al. 2008; Simatupan y Sridharan, 2002; Sana et al., 2014; Salas Navarro et al., 2016), dicho acuerdo supone negociar decisiones de índole estratégico -planeación de producción y distribución- y de índole operativo -programación y reprogramación de producción- (Lin H.W. et al. 2009; Bustamante, 2009), dichas empresas se unen con el objetivo de atender proyectos que demanden una elevada capacidad de respuesta, la cual no podría ser soportada individualmente por alguno de los elementos de la cadena, estas entidades colaboran para alcanzar objetivos comunes o compatibles de una mejor manera. La programación y reprogramación de producción de la red colaborativa, usualmente es generada por una o varias de las firmas que actúa (n) como coordinador (es) (Fisher, 1994; Lee et al. 1997; Horvath, 2001). De hecho, diversos autores debaten sobre la necesidad de establecer estructuras de centralización en diversas decisiones, antes de iniciar la implementación de estrategias de colaboración total, así mismo la centralidad en una cadena de suministro puede darse con el fin de implementar coordinación de tareas de cierto tipo y ello no implica asignación total de responsabilidades a los agentes centrales (Kjenstad, 1998).

Las técnicas y modelos aplicados en la programación y reprogramación de producción en la red colaborativa deben tener en cuenta variables y parámetros del sistema de manera integral para obtener la solución óptima para todas las entidades participantes de la red colaborativa (Kalwani y Narayandas, 1995). Este proceso es por lo general muy complejo debido al gran número de objetivos en conflicto, las variaciones impredecibles de rendimiento y sus posibles soluciones alternativas. Con el uso de técnicas convencionales de optimización global a menudo no es fácil llegar a una solución conveniente para problemas tan complejos, ya que es difícil de modelar todos los objetivos y las limitaciones. Estas tareas se complican aún más cuando se dispone de un período de tiempo limitado e incompleto de acuerdo a las perspectivas de todas las entidades involucradas en la red (Simón, 1977).

En este artículo se hace una revisión de la literatura en la reprogramación de la producción en cadenas de suministro colaborativas. En la siguiente sección se presenta una revisión de las investigaciones relacionadas con la gestión en cadenas de suministro, haciendo especial énfasis en los problemas y metodologías de solución para la reprogramación de la producción en ambientes colaborativos. De igual forma, se presenta un análisis Cienciométrico de las publicaciones, investigaciones, autores e instituciones que se destacan en el ámbito de estudio.

La metodología de este trabajo busca minimizar los posibles sesgos del observador en una revisión sistemática de la literatura. Para esto se han definido unas preguntas orientadoras de trabajos de referencia (Ovallos-Gazabón et al., 2016; Viana-Ruiz & Montes Hincapié, 2015).

2.1. Preguntas orientadoras

Pregunta 1: ¿Qué es la reprogramación de la producción?

Pregunta 2: ¿Cómo se lleva a cabo la reprogramación de la producción en cadenas de suministro en ambientes colaborativos?

Pregunta 3: ¿Cómo se clasifican los modelos de programación y reprogramación de la producción de acuerdo a su objetivo, técnica heurística o meta-heurística utilizada o estructura de la cadena de suministro?

Pregunta 4: ¿`Como son los esquemas de reprogramación de la producción en cadenas de suministro colaborativas?

Pregunta 5: ¿Cuáles son los autores, instituciones y países más destacados en la temática?

2.2. Estrategia de búsqueda, recolección y análisis de la información

La presente revisión se hace en las bases de datos científicas Scopus, ScienceDirect, Emeralrd, Taylor and Francis. Para el análisis de la información se emplean las herramientas que proveen las bases de datos mencionadas; la recolección de información se llevó a cabo entre los meses de enero a octubre de 2016.

Es posible clasificar los modelos de programación y reprogramación de producción de acuerdo a los siguientes aspectos: i) objetivo del modelo, ii) técnica heurística o meta-heurística utilizada, iii) estructura de la cadena de suministro colaborativa.

El primer criterio de clasificación está relacionado con los objetivos del modelo de programación/reprogramación en cuestión. El objetivo puede ser único o puede plantearse un modelo multiobjetivo. Hoogeveen (2005) considera como los principales criterios de optimización en modelos de programación y reprogramación de producción los siguientes: la minimización del tiempo máximo de finalización de los trabajos (makespan), minimización la tardanza ponderada, minimización de la tardanza total, minimización del retardo ponderado, minimización del retardo máximo y minimización del número de trabajos retrasados. Se puede afirmar que un buen horario suele ser un programa que es capaz de cumplir o equilibrar una amplia cantidad de objetivos y preferencias conflictivas (Sadeh et al. 1995).

Los objetivos de las empresas involucradas en una red colaborativa orbitan entorno a generar óptimos niveles de servicio, lo que implica disponer de eficientes sistemas de distribución de los productos hasta los clientes finales, la entrega de la mayor cantidad de órdenes a los clientes en las fechas requeridas y minimización de los costos asociados (Bustamante, 2009). Sobre el particular la mayoría de las redes colaborativas y demás sistemas de negocio establecen una penalización por entregas tardías o, bien sobrecostos por productos terminados antes de la fecha estipulada o adelantados. Por esa razón muchos esquemas de programación están diseñados para minimizar la tardanza o el adelanto de los pedidos o ambos al tiempo -multiobjetivo- por medio de lo cual se busca minimizar el impacto de las penalizaciones antes mencionadas (Valente y Alves (2007). Este enfoque es compatible con estructuras centralizadas y estructuras basadas en la cultura justo a tiempo, la cual plantea que los productos deben ser entregados cuando “se requiera” lo que va en contravía con la presencia de tardanza y adelanto de trabajos (Agnetis et al. 2001). Los modelos de programación y reprogramación de redes colaborativas pueden o no castigar equitativamente la tardanza y el adelanto, por ejemplo, algunos autores plantean castigar más fuertemente el retraso, con la intención de evitar horarios en los que un trabajo o sólo unos pocos aporten la mayor parte de los costos (Valente y Alves (2007).

Otro enfoque es el que plantea modelos de programación y reprogramación de producción que buscan minimizar el llamado makespan o el tiempo máximo de finalización de los trabajos, dicho tiempo de finalización desde un enfoque de red colaborativa no solo incluye el tiempo consumido por el trabajo en el eslabón productivo, sino también el tiempo destinado al transporte del producto, es decir mide el tiempo que va desde el inicio de la producción en el primer eslabón de la red colaborativa, hasta la entrega final del mismo al cliente final (Sha y Hsu, 2006; Zhang y Wu, 2006). Otros modelos se decantan por minimizar el tiempo de inactividad de las máquinas y recursos, hecho que se presenta principalmente cuando los costos de operación son elevados y la demanda es superior a la capacidad instalada (Korman, 2002; Landis, 1993).

El segundo criterio de clasificación esta relación con la heurística o metaheurística utilizada en el desarrollo del modelo de programación/reprogramación de la red colaborativa. La ineficiencia para encontrar una solución óptima al problema en instancias moderadamente grandes por parte de los métodos exactos (programación matemática), da origen a la utilización de los métodos o algoritmos de aproximación (heurísticas y metaheuristicas) los cuales aunque no garantizan la obtención de una solución óptima, usan estrategias que permiten encontrar de modo eficiente una solución factible (que satisfaga las restricciones del problema) cercana a un óptimo o inclusive algunas veces encontrar una solución óptima, en caso de que dicha solución exista (Rivera, 2007).

Dentro de las razones que llevarían a utilizar un método aproximado dentro de un problema de programación y reprogramación de producción en cadenas de suministro colaborativas están: la no existencia de un método exacto que atienda el problema en cuestión, la inviabilidad de uno existente, la no necesidad de determinar la solución optima del problema, cuando encontrar la misma es muy difícil, cuando los datos son poco fiables, necesidad de tiempos cortos de ejecución y la no existencia de recursos para implementar la metodología exacta (Martí, 2003).

Los procedimientos metaheurísticos se sitúan conceptualmente por encima de los heurísticos clásicos (o de propósito general) en el sentido de que guían el diseño del algoritmo. Así al enfrentar un problema de optimización, puede escogerse cualquiera de estos métodos para diseñar un algoritmo específico que lo resuelva de manera aproximada (Osman y Nelly, 1996). Algunos de los metaheurísticos más utilizados recientemente para la programación y reprogramación de producción en redes colaborativas son los siguientes: búsqueda local, recocido simulado, búsqueda tabú, búsqueda en vecindarios variables, algoritmos genéticos, sistemas de colonias de hormigas y métodos híbridos. Los métodos híbridos reciben un gran interés entre los métodos heurísticos/metaheurísticos y en general en optimización. Los mejores resultados encontrados para muchos problemas de optimización prácticos o académicos se han obtenido con algoritmos híbridos (Talbi, 2002). La idea principal de la construcción de métodos híbridos es aprovechar las fortalezas y compensar las debilidades de dos o más métodos de búsqueda complementarios (Sait y Youssef, 1999).

El tercer criterio de clasificación está relacionado con la estructura o configuración de los elementos de la red colaborativa. Las cadenas de suministro colaborativas a menudo integran diversas entidades productoras con otras que se encargan de la distribución, por lo que el abanico de posibles estructuras de cadenas de suministro es bastante grande (Brockhoff y Hauschildt, 1993; Wildemann, 1997; Steven, 2001). Podemos hablar de estructuras constituidas por un eslabón dedicado a la fabricación de los bienes (eslabón productivo) y un sistema de transporte que envía los productos a uno o varios destinos, así como varios eslabones productivos comunicados por un sistema de transporte intermedio, entre otras (Sarmiento y Nagi, 1999; Erenguc et al. 1999; Tseng y Jiao, 1996). Por lo general entre las etapas de producción y distribución existe un inventario intermedio, a menudo estas estructuras están vinculadas a decisiones de inventario. La coordinación puede lograrse mediante la programación integrada de la producción y la distribución y el objetivo debe ser el de alcanzar el nivel más alto de servicio y alcanzar un equilibrio entre el costo total del inventario de cadena de suministro, los tiempos de entrega, los gastos de envío y los demás gastos de producción y de distribución (Fei et al. 2009).

Las redes colaborativas que implican un solo eslabón productivo pueden parecer poco comunes, sin embargo, son muy comunes en sectores como el químico y el farmacéutico (Valente y Alves (2007). Además, a menudo el rendimiento de una red colaborativa depende de la calidad de la programación que se ejecuta en los eslabones críticos o cuellos de botella. El enfoque de programación de una o varias máquinas ayuda a proporcionar una visión más completa en problemas de programación que implican la sincronización y coordinación de eslabones de una cadena de suministro. De hecho, diversos problemas de programación coordinada de redes colaborativas implican la resolución de subproblemas de programación de una sola maquina (Wagner, 2002).

Los modelos implementados en estructuras que integran producción y distribución por lo general tratan de sincronizar el orden de producción en la planta con la programación de las entregas, teniendo en cuenta los ingresos, los costos y los niveles de servicio al cliente (Chen, 2010). Desde el punto de vista de la colaboración la integración de la producción y distribución a nivel individual de cada empresa, es tan importante como los acuerdos de integración celebrados globalmente entre las mismas, Chen y Vairaktaris (2005) y Pundoor y Chen (2006) muestran que hay un beneficio significativo mediante el uso óptimo de la producción integrada de distribución  tanto a nivel interno como a nivel externo, producto en parte a la exigente competencia en el mercado global de hoy y las crecientes expectativas de los clientes. Además, si las tareas de programación y reprogramación de producción y decisiones de transporte se llevan a cabo al mismo tiempo es posible generar un entorno de programación mucho más realista, obtener un mayor rendimiento y una mayor productividad dentro del sistema de fabricación (Chen, 2000).

Dentro de los esquemas de colaboración en cadenas de suministro diferentes autores lo han abordado a través de la teoría de juegos para determinar si es estable la colaboración y razonable compartir beneficios que conjuntamente se obtienen. Nash (1950) y Shapley (1953) desarrollaron el concepto de teoría de juegos que permite determinar la forma razonable de compartir beneficios que conjuntamente se obtienen de ella. Dentro de la teoría de juegos la planificación colaborativa en la cadena de suministro permite los procesos de toma de decisiones con diferentes jugadores, tácticas, roles y escenarios (Stewart & Fenn, 2006).

3.1. Metodologías aplicadas en la reprogramación de la producción en redes colaborativas

Los esquemas de reprogramación de la producción en una cadena de suministro colaborativa deben enfrentarse a diversos factores de variabilidad tales como nuevos pedidos, retraso en el suministro de materiales, averías en máquinas y fallas en la producción, además deben ser capaces de actualizar los horarios de acuerdo a restricciones y supuestos cambiantes (Dorn, 2001). En la práctica los esquemas de programación reactiva intentan resolver los problemas generados por las perturbaciones de manera local, sin embargo, cuando los problemas no pueden resolverse localmente o el calendario modificado influye de manera negativa en los de las demás empresas -de la red colaborativa-, se inicia un proceso de programación reactiva en el nivel superior o en el agente central perteneciente a la red (Sauer et al. 2001).

Vergara et al. (2002) estudian la coordinación entre diferentes miembros de las cadenas de suministro y desarrollan un algoritmo evolutivo para la sincronización óptima de las cadenas de suministro utilizando un modelo económico y de programación. Moon et al. (2002) proponen un proceso de planificación integrada y la programación de una cadena de suministro para minimizar el adelanto total de los pedidos y desarrollan un algoritmo genético para el modelo. Lee et al. (2002) estudian problemas de selección de la máquina simultáneamente a la secuenciación y la externalización de decisiones en un modelo integrado para minimizar el makespan para lo cual desarrollan un enfoque basado un algoritmo genético para resolver el modelo. Ortiz et al. (2015) estudian el problema de programación de flexible job shop incluyendo el throughput para minimizar la tardanza en la asignación de órdenes a las máquinas. En la Tabla 1 se presentan las principales investigaciones que abordan la reprogramación de la producción en redes o cadenas de suministro colaborativas.

Tabla 1. Investigaciones destacadas en reprogramación de la producción en cadenas de suministro colaborativas.

3.2. Análisis Cienciométrico

Al revisar las principales bases de datos de publicaciones científicas se encuentra que el término: “Reactive Scheduling in Collaborative Supply Chain” aparece a partir del año 1988 y se ha venido incrementando en número de publicaciones en los últimos años. En el gráfico 1 se presentan el número de publicaciones relacionadas con el tema en bases de datos científicas como Scopus, Science Direct, Emerald y Taylor & Francis, en las cuales se identifica una tendencia de aumento del número de trabajos generados en los últimos años. Se observa que Scopus y Science Direct presentan un mayor número de trabajos del tema, debido a que concentran a las revistas que más publican en “reactive scheduling” o reprogramación de la producción, tales como International Journal of Production Research, International Journal of Production Economics, Computers and Chemical Engineering, Expert Systems with Applications y European Journal of Operational Research.

Gráfico 1. Número de Publicaciones por año. Fuente: Bases de Datos Bibliográficas.

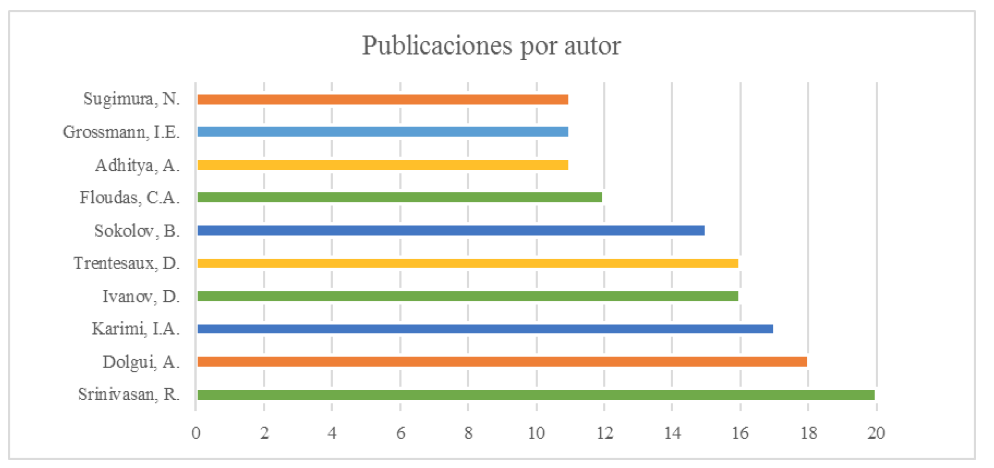
Al revisar las diferentes bases de datos se encuentra que muchos autores han realizado entre once o veinte publicaciones referente a la gestión del riesgo en cadenas de suministro colaborativas, como se observa en el gráfico 2.

Gráfico 2. Publicaciones por autor. Fuente: Scopus®.

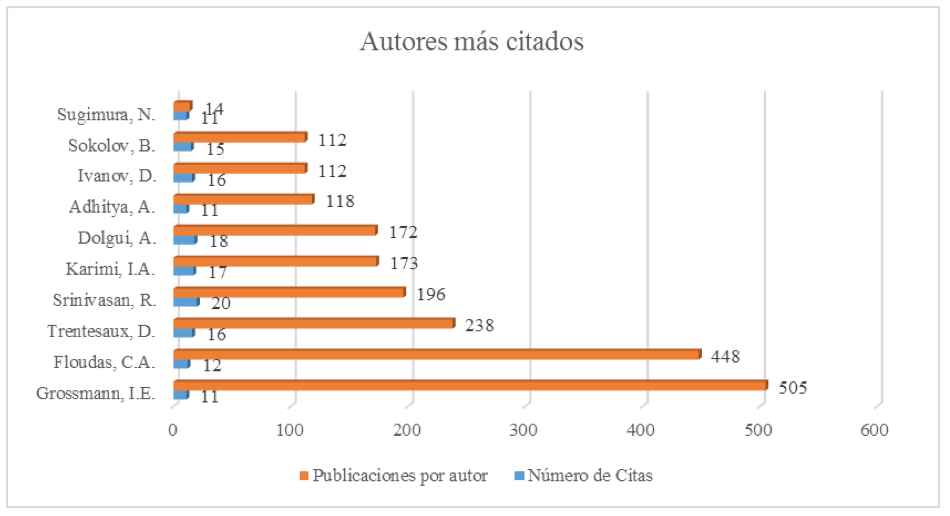
Al ser un tema que ha tomado interés en lo últimos años, los artículos publicados han sido citados muchas veces; por lo que se destacan publicaciones como la de Battaia & Dolgui (2013) con 129 citas, Verderame et al. (2010) con 96 citas, Trentesaux (2009) con 88 citas, Van Den Heever & Grossmann (2003) con 71 citas y Li et al. (2007) con 49 citas. En el gráfico 3 se presentan las citas que ha recibido los trabajos publicados por los principales autores en la temática de reprogramación de la producción de cadenas de suministro colaborativas.

Gráfico 3. Autores más citados por sus trabajos en el área. Fuente: Scopus®

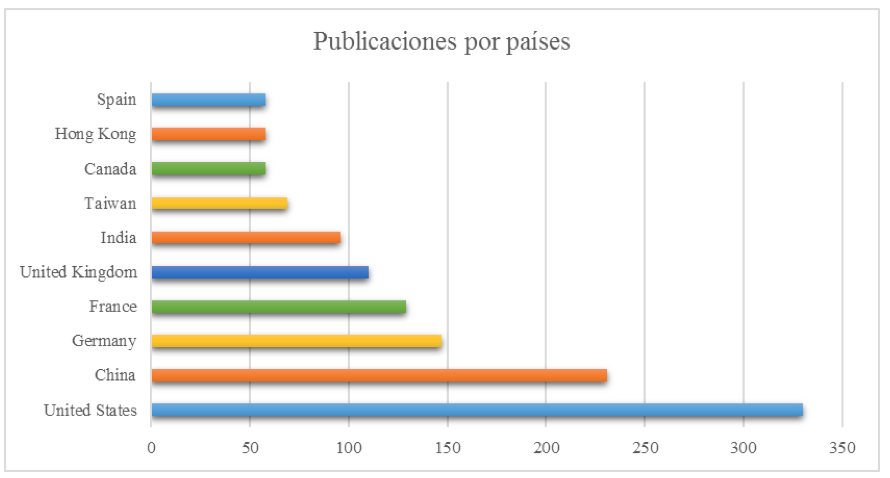
La reprogramación de la producción en cadenas de suministro colaborativas se publica con frecuencia en países como Estados Unidos, China, Alemania, Francia y United Kingdom. En el gráfico 4 se presentan los países que lideran la producción de publicaciones científicas relacionadas con la temática objeto de estudio.

Gráfico 4. Países que más publican la temática. Fuente: Adaptación de Scopus®.

Las cinco primeras instituciones en cuanto a producción científica relacionada con el tema de reprogramación de la producción en cadenas de suministro colaborativas son: Hong Kong Polytechnic University, National University of Singapore, Universite de Valenciennes et du Hainaut Cambresis, Carnegie Mellon University y The University of Hong Kong (Ver Gráfico 5).

Gráfico 5. Producción por Instituciones. Fuente: Adaptación de Scopus®

En una cadena de suministro tradicional la volatilidad de los mercados y de las decisiones de los demás miembros de la cadena hace que resulte inevitable que se produzcan cambios en los parámetros, en consecuencia, se debe garantizar que el programa de producción sea capaz de aportar una respuesta de una manera flexible y ágil. Sin embargo, el intercambio de información entre diferentes agentes para gestionarse de una manera colaborativa que beneficie a toda la cadena de suministro, permite reducir los niveles de indeterminación de los parámetros del modelo de programación/reprogramación, lo que conlleva a que dichos programas puedan ofrecer resultados con una mayor precisión.

El uso de heurísticas y metaheuristicas para programar cadenas de suministro colaborativas o redes colaborativas es un campo de investigación en pleno crecimiento, demostrado en la poca literatura relacionada al tema (en comparación con otros temas derivados). Sin embargo, podemos encontrar como dichos esquemas son construidos para lidiar con una visión global -y no local- de la red de suministro, determinando estrategias para manejar posibles conflictos operativos entre los diferentes eslabones y entre los sistemas de planificación y programación/reprogramación. Las heurísticas y metaheuristicas permiten construir modelos que integren eslabones productivos de diverso patrón de fabricación y de distribución, generándose funciones objetivo que deben tener en cuenta no solo los tiempos de producción, sino también tiempos de transporte, de entrega final, consideraciones en cuanto a alistamientos y los costos totales.

Se observa como las heurísticas y metaheuristicas permiten desarrollar planteamientos de funciones objetivo de maneras que sería difícilmente solucionables por métodos exactos, principalmente cuando se trabajan enfoques multicriterio. Además planteamientos de algoritmos genéticos, recocido simulado, búsqueda tabú, búsqueda local, optimización por nube de partículas, optimización por colonia de hormigas entre otros, son aplicados en diversas configuraciones o esquemas de producción caracterizándose por la posibilidad que brindan de obtener, además de las secuencia de fabricación, aspectos adicionales como ruta que debe seguir el producto en la planta de producción, tamaño de los lotes, programación de tiempos de alistamientos, programación de tiempos muertos, así mismo encontramos esquemas que pueden secuenciar hasta 1000 trabajos al tiempo demostrando la gran potencia de los mismos.

El avance más significativo en cuanto a heurísticas y meta heurísticas, aplicadas a programación y reprogramación e producción, son los llamados enfoques híbridos, esto se debe a que cada técnica parece tener unas bondades especiales identificables por ejemplo la capacidad de muestreo estadístico del recocido simulado, la potencial memoria adaptativa del esquema búsqueda tabú y la potencia de búsqueda del algoritmo genético, pueden combinarse con algunas características específicas de otros algoritmos para construir uno que sea superior en robustez y eficiencia. Investigar como estos enfoques híbridos pueden ayudar a generar programas con una mayor eficiencia puede ser un campo de investigación a futuro.

Adhitya, A., Srinivasan, R., Karimi, I.A. (2004). A heuristic reactive scheduling strategy for recovering from refinery supply chain disruptions, Laboratory for Intelligent Applications in Chemical Engineering Department of Chemical and Biomolecular Engineering, National University of Singapore.

Agarwal, R., Ergun, O., Orlin, J., Potts, C. (2004). Solving Parallel Machine Scheduling Problems with Variable Depth Local Search, ÄOzlem Ergun, oergun@isye.gatech.edu, 404-894-2369.

Aggoune, R. (2004). Minimizing the makespan for the flow shop scheduling problem with availability constraints, European Journal of Operational Research, Vol. 153, pp. 534-543.

Agnetis, A., Detti, P., Meloni, C., Pacciarelli, D. (2001). Set-up coordination between two stages of a supply chain. Annals of Operations Research, Vol. 107(1-4), pp. 15-32.

Akrami, B., Karimi, B., Moattar-Hosseini, S.M. (2006). Two metaheuristic methods for the common cycle economic lot sizing and scheduling in flexible flow shops with limited intermediate buffers: the finite horizon case. Applied Mathematics and Computation, Vol. 183, pp. 634-45.

Anand, Mendelson, H. (1997). Information and Organization for Horizontal Multimarket Coordination. Management Science. Vol. 43(12), pp. 1609-1627.

Anghinolfi, D., Paolucci, M. (2007). Parallel machine total tardiness scheduling with a new hybrid metaheuristic approach, Computers & Operations Research, Vol. 34, pp. 3471-3490.

Anis Allouche, M. (2010). Manager’s Preferences Modeling Within Multi-Criteria Flowshop Scheduling Problem: A Metaheuristic Approach. Unité de Recherche en Gestion Industrielle et Aide à la Décision, Faculté des Sciences Economiques et de Gestion, Université de Sfax, Sfax. Tunisia.

Armentano, V.A., Arroyo, J.E.C. (2004). An Application of a Multi-Objective Tabu Search Algorithm to a Bicriteria Flowshop Problem. Journal of Heuristics, Vol. 10: pp. 463-481.

Arshinder, Kanda,A., Deshmukh, S. G. (2008). Supply chain coordination: Perspectives, empirical studies andre search directions. International Journal of Production Economics, Vol. 115, pp. 316-335.

Battaia, O., Dolgui, A. (2013). A taxonomy of line balancing problems and their solution approaches. International Journal of Production Economics. Vol. 142 (2), pp. 259-277.

Behnamian, J., Ghomi, F. (2010). Parallel Machines Scheduling with Dual Criteria and Sequence-dependent Setups: Cooperative Metaheuristics, Proceedings of the 2010 IEEE IEEM.

Ben-Daya, M., Al-Fawzan, M. (1998). A tabusearch approach for the flow shop scheduling problem. European Journal of Operational Research, Vol. 109, pp. 88-95.

Berning, G., Brandenburg, M., Gürsoy, K., Kussi, J.S., Mehta, V., Tölle, F. (2004). Integrating collaborative planning and supply chain optimization for the chemical process industry (I) - methodology. Computers and Chemical Engineering, Vol. 28 (6–7), pp. 913-927.

Binato, S., Hery, W.J., Loewenstern, D.M., Resende, M.G.C., (2002). A GRASP for Job Shop Scheduling. In: Essays and Surveys in Metaheuristics, Ribeiro, Celso C., Hansen, Pierre (Eds.), Kluwer Academic Publishers.

Blazewicz, J., Pesch, E., Sterna, M., Werner, F. (2005). Metaheuristic Approaches for the Two-Machine Flow-Shop Problem with Weighted Late Work Criterion and Common Due Date.

Brandimarte, P. (1993). Routing and scheduling in a flexible job shop by tabu search. Annals of Operations Research, Vol. 41, pp. 157-183.

Britto, R., Delgadillo, G., Caballero, J. (2007). Production Programming in Manufacturing Systems (Workshop Type) with a Combined Mobile Bottleneck and Taboo Search Algorithm, Ing. Univ. Bogotá (Colombia), Vol. 11 (2), pp. 203-224.

Cai, B., Wang, S., Hu, H. (2011). An Effective Hybrid Genetic Algorithm for Job Shop Scheduling Problem, World Academy of Science, Engineering and Technology, Vol. 58.

Chambers, J.B., Barnes, J.W. (1996). Flexible job shop scheduling by tabu search .graduate program in operations research and industrial engineering. The University of Texas at Austin, technical report series ORP96-09.

Chambers, J.B., Barnes, J.W. (1996). Reactive search for flexible job shop scheduling. graduate program in operations research and industrial engineering. The University of Texas at Austin, technical report series ORP98-100.

Chan, F.T.S., Chung, S.H., Chan, P.L.Y. (2005). An adaptive genetic algorithm with dominated genes for distributed scheduling problems. Expert Systems with Applications, Vol. 29 (2), pp. 364-371.

Chang, Y., Lee, C. (2004). Machine scheduling with job delivery coordination. European Journal of Operational Research, Vol. 158 (2), pp. 470-487.

Chen, F. (1999). Decentralized Supply Chains subject to Information Delays, Management Science, Vol. 45(8), pp. 1076-1090.

Chen, J.M., Chen, T.H. (2005). The Multi-item Replenishment Problem in a Two-Echelon Supply Chain: The Effect of Centralization versus Decentralization. Computers & Operations Research, Vol. 32, pp. 3191-3207.

Chen, P. (2000). Integrating production and transportation scheduling in a make-to-order environment. Ph.D. thesis, University of Cornell.

Chen, Z.-L., Pundoor, G. (2006). Order assignment and scheduling in a supply chain. Oper. Res, Vol. 54, pp. 555-572.

Chen, Z.-L., Vairaktarakis, G. L. (2005). Integrated scheduling of production and distribution operations, Management Sci, Vol. 51, pp. 614-628.

Cheng-Hsiang Liu, Bor-Yuh Leu, Sheng-Yuan Hsu. (2012). Scheduling of parallel machines with job delivery coordination, International Journal of Innovative Computing, Information and Control, Volume 8, Number 1(B).

Cheng-Hsiang Liu, Tzu-Ling Wu, Pei-Shiun Lin (2010). A Hybrid Genetic Algorithm-based Approach to Solve Parallel Machine Scheduling with Job Delivery Coordination, Proceedings of the International MultiConference of Enfineers and Computer Scjentists, Vol. 3, Hong Kong.

Ching-Jong Liao, Cian-Ci Shyu, Chao-Tang Tseng. (2009). A least flexibility first heuristic to coordinate setups in a two- or three-stage supply chain, Int. J. Production Economics, Vol. 117, pp. 127–135.

Chiou, C., Chen, W., Liu, C., Wu, M. (2012). A genetic algorithm for scheduling dual flow shops. Expert Systems with Applications. Vol. 39, pp. 1306-1314.

Chi-Shiang Su, Jason Chao-Hsien Pan, Tsung-Shin Hsu (2009). Theoretical Computer Science, Vol. 410, pp. 2581-2591.

Chung-Lun Li, Jinwen Ou. (2006). Coordinated Scheduling of Customer Orders with Decentralized Machine Locations, Department of Logistics The Hong Kong Polytechnic University Hung Hom, Kowloon, Hong Kong.

Cochran, J.K., Horng, S.M., Fowler, J.W. (2003). A multipopulation genetic algorithm to solve multi-objective scheduling problems for parallel machines” Computers and Operations Research, Vol. 30, pp.1087-1102.

Crauwels, H. (1995). Local search heuristics for single-machine scheduling with batching to minimize the number of late jobs, European Journal of Operational Research, Vol. 90, pp. 200-213.

Crauwels, H. (1995). Local search heuristics for single-machine scheduling with batching to minimize the number of late jobs, European Journal of Operational Research, Vol. 90, pp. 200-213.

Dannenbring, D., (1977). An evaluation of flow shop sequencing heuristics. Management Science, Vol. 23, pp. 1174-1182.

Dorn, J., (1995). Iterative Improvement Methods for Knowledge-based Scheduling. AI Comunications, Vol. 8(1), pp. 20-34.

Duan, J., Pan, Q., Li, J., Bao, K. (2010). Harmony Search Algorithm. Sixth International Conference on Natural Computation.

Durfee, E. H. (1999). Distributed problem solving and planning, in Multi-Agent Systems: A Modern Approach to Distributed Artificial Intelligence. Cambridge, MA: MIT Press, ch. 3.

Erenguc, S. S., Simpson, N. C., Vakharia, A. J. (1999). Integrated production/ distribution planning in supply chains: An invited review. Eur. J. Oper. Res. Vol. 115, pp. 219-236.

Feldmann, M., Biskup, D. (2003). Single-machine scheduling for minimizing earliness and tardiness penalties by meta-heuristic approaches, Computers & Industrial Engineering, Vol. 44, pp. 307-323.

Fernandes, S., Lourenço, H. (2007). A simple optimized search heuristic for the job-shop scheduling problem, Universidade do Algarve, Faro, Portugal - Univertitat Pompeu Fabra, Barcelona, Spain.

Fowler, J.W., Horng, S., Cochran, J.K. (2003). A hybridized genetic algorithm to solve parallel machine scheduling problems with sequence dependent setups. International Journal of Industrial Engineering, Vol. 10(3), pp. 232-43.

Framinan, J.M., Leisten, R. (2008). A multi-objective iterated greedy search for flowshop scheduling with makespan and flowtime criteria. OR Spectrum, Vol. 30(4), pp. 787-804.

Franca, P., Gendreau, M., Laporte, G., Mnller, F. (1996). A tabu search heuristic for the multiprocessor scheduling problem with sequence dependent setup times. International Journal of Production Economics, Vol. 43, pp. 79-89.

Gagne, C., Gravel, M., Price, W.L. (2005). Using Metaheuristic Compromise Programming for the Solution of Multiple Objective Scheduling Problems”. Journal of the Operational Research Society, Vol. 56(6), pp. 687-698.

Gangadhran, R., Rajendran, C. (1994). A Simulated Annealing Heuristic for Scheduling in a Flow-Shop with Bicriteria. Computers and Industrial Engineering, Vol. 27, pp. 473-476.

Gao, J., Sun, L., & Gen, M. (2008). A hybrid genetic and variable neighborhood descent algorithm for flexible job shop scheduling problems. Computers & Operations Research, Vol. 35, pp. 2892-2907.

Gendreau, M., Laporte, G., Morais-Guimaraes, E. (2001). A divide and merge heuristic for the multiprocessor scheduling problem with sequence dependent setup times. European Journal of Operational Research, Vol. 133, pp. 183-189.

Gomez A., Cuevas R., De la Fuente D., Parreno J., Priore P. (2008). New Metaheuristic for the Job Shop Scheduling Problem with PSO, Department Administration de Empresas, Oviedo University, Asturias, Spain.

Gonçalves, J., de Magalhães, J., Resende, M. (2002). A Hybrid Genetic Algorithm for the Job Shop Scheduling Problem,

Gong, H., Tang, L. (2008). Two-machine flowshop scheduling problem with transportation and blocking features, Chinese control and decision conference (CCDC, 2008), National 863 High-Tech Research and Development Program of China through approved.

Gordon, V., Strusevich, V. (2009). Single machine scheduling and due date assignment with positionally dependent processing times, European Journal of Operational Research Vol. 198, pp. 57-62.

Gravel, M., Price, W.L., Gagne C. (2000). Scheduling jobs in an alcan aluminium foundry using a genetic algorithm. International Journal of Production Research, Vol. 38, pp. 3031-41.

Grosan, C. (2009). A Multiobjective Metaheuristic For Job-Shop Scheduling, Studia Univ. Babes Bolyai, Informatica, Volume LIV, Number 1.

Guinet, A. (1993). Scheduling sequence-dependent jobs on identical parallel machines to minimize completion time criteria. International Journal of Production Research, Vol. 31, pp. 1579-1594.

Gupta, J., (1971). A functional heuristic algorithm for the flow shop scheduling problem. Operations Research Quarterly, Vol. 22, pp. 39-47.

Haddock, J., O’Keefe, R. M., (1990). Using artificial intelligence to facilitate manufacturing systems simulation. Computers and Ind. Engng, Vol. 18(3), pp. 275-283.

Hall, N. G., Potts, C. N. (2003). Supply chain scheduling: Batching and delivery. Operations Research, Vol. 51, pp. 566-584.

Hall, R. W. (1983). Zero Inventories. Dow Jones-Irwin, 1983, ISBN 0-87094-461-4.

Handfield R. B., Eenest, L. N. (1999). Introduction to supply chain management, Prentice-Hall, Upper Saddle River.

Holweg, M., Disney, S., Holmstro, J., Smaros, J. (2005). Supply Chain Collaboration. Making Sense of the Strategy Continuum. European Management Journal.  Vol. 23, No. 2, pp. 170-181.

Hongyan, X., Hong, H. (2010). Research on Job-Shop Scheduling Problem Based on Self-Adaptation Genetic Algorithm, School of Management, Harbin University of Commerce, Harbin 150070, China.

Hoogeveen, H., (2005). Multi-criteria scheduling. European journal of operational research

Hsu, C., Sha, D. (2006). A hybrid particle swarm optimization for job shop. Computers & Industrial Engineering, Vol. 51(4), pp. 791-808.

Hurink, E., Jurisch, B., Thole, M. (1994). Tabu search for the job shop scheduling problem with multi-purpose machine. Operations Research Spektrum, Vol. 15, pp. 205-215.

Hurink, J., Knust, S. (2001). List scheduling in a parallel machine environment with precedence constraints and setup times. Operations Research Letters, Vol. 29, pp. 231-239.

Husseinzadeh, A., Karimi, B., Jenabi, M. (2008). A hybrid genetic heuristic for scheduling parallel batch processing machines with arbitrary job sizes, Computers & Operations Research, Vol. 35, pp. 1084-1098.

Jain, A.S., Meeran, S. (1999). A State-of-the-Art Review of Job-Shop Scheduling Techniques. European Journal of Operational Research, Vol. 113, pp. 390-434. AT&T Labs Research Technical Report TD-5EAL6J.

Janiak, A., Kozan, E., Lichtenstein, M., Oguz, C. (2007). Metaheuristic approaches to the hybrid flow shop scheduling problem with a cost-related criterion, Int. J. Production Economics, Vol. 105, pp. 407-424.

Jenabi, M., Fatemi-Ghomi S., Torabi, S., Karimi B. (2007). Two hybrid meta-heuristics for the finite horizon ELSP in flexible flowlines with unrelated parallel processors. Applied Mathematics and Computation, Vol. 186(1), pp. 230-45.

Jia Hua Weng, Hiroki Okubo, Hisashi Onari. (2000). Flexible Assembly Job Shop Scheduling Based on Tabu Search, Dept. of Industrial & Management Systems Engineering, Waseda University.

Johnson, S.M., (1954). Optimal two- and three stage production schedules with set up times included. Naval Research Logistics Quarterly, Vol. 1, pp. 61-68.

Jou, C. (2005). A genetic algorithm with sub-indexed partitioning genes and its application to production scheduling of parallel machines. Computers & Industrial Engineering, Vol. 48, pp. 39-54.

Jula, P., Rafey, A. (2010). Coordinated scheduling of a single machine with sequence dependent setup times and time window constraints, International Journal of Production Research, Vol. 00, No. 00.

Kaczmarczyk, W., Sawik, T., Schaller, A., Tirpak, TM. (2004). Optimal versus heuristic scheduling of surface mount technology lines. International Journal of Production Researc, Vol. 42(10), pp. 2083-110.

Kelly, J.D., Zyngier, D., (2008). Hierarchical Decomposition Heuristic for Scheduling: Coordinated Reasoning for Decentralized And Distributed Decision-Making Problems. Computers and Chemical Engineering, Vol. 32, pp. 2684-2705.

Kerr, R. M., Ebsary, R. W. (1998) Implementation of an expert system for production scheduling. European journal of operational research, Vol. 33, pp.17-29.

Khalouli, S., Ghedjati, F., Hamzaoui, A. (2010). The meta-heuristic approach to solve a JIT scheduling problem in hybrid flow shop, Engineering Applications of Artificial Intelligence, Vol. 23, pp. 765-771.

Kim, C., Shin, H. (2003). Scheduling jobs on parallel machines: a restricted tabu search approach. International Journal of Advanced Manufacturing Technology, Vol. 22, pp. 278-287.

Kim, D., Kim, K., Jang, W., Chen, F. (2002). Unrelated parallel machine scheduling with setup times using simulated annealing. Robotics and Computer Integrated Manufacturing, Vol. 18, pp. 223-231.

Kjenstad, D. (1998). Coordinated supply chain scheduling, Norwegian university of Science and Technology, Department of Production and Quality Engineering.

Krishnan, M., Karthikeyan, T., Chinnusamy, T. R., Venkatesh Raja, K. (2012). A Novel Hybrid Metaheuristic Scatter Search-Simulated Annealing Algorithm for Solving Flexible Manufacturing System Layout, European Journal of Scientific Research, Vol.73 No.1, pp. 52-61.

Kumar, R., Tiwari, M. K., Shankar, R. (2008). Scheduling of flexible manufacturing systems: an ant colony optimization approach, Proc. Instn Mech. Engrs Part B: J. Engineering Manufacture, Vol. 217.

Kunpeng Li, Appa Iyer Sivakumar, Viswanath Kumar Ganesan. (2008). Analysis and algorithms for coordinated scheduling of parallel machine manufacturing and 3PL transportation. Int. J. Production Economics. Vol. 115, pp. 482-491.

Kurz, M., Askin, R. (2001). Heuristic scheduling of parallel machines with sequencedependent set-up times. International Journal of Production Research, Vol. 39, pp. 3747-3769.

Kurz, M.E., Askin, R.G. (2004). Scheduling flexible flow lines with sequence-dependent setup times. European Journal of Operational Research, Vol. 159, pp. 66-82.

Lapierre, S.D., Ruiz, A.B. (2007). Scheduling logistic activities to improve hospital supply systems. Computers and Operations Research, Vol. 34 (3), pp. 624-641.

Lee, C.Y. (1997). Minimizing the makespan in the two-machine flow-shop scheduling problem with an availability constraint, Operational Research Letters, Vol. 20, pp. 129-139.

Lee, C.Y., Chen, Z.L. (2001). Machine scheduling with transportation considerations, Journal of Scheduling, Vol. 4, pp. 4-24.

Lee, H. L., Whang, S. (1999). Decentralized Multi-Echelon Supply Chains: Incentive and Information, Management Science, Vol. 45(5), pp. 633-640.

Lee, H., Billington, C. (1992). Managing Supply Chain Inventory: Pitfalls and Opportunities. Sloan management review.

Lee, Y. H., Jeong, C. S., Moon, C. (2002). Advanced planning and scheduling with outsourcing in manufacturing supply chain. Computers & Industrial Engineering, Vol. 43, pp. 351-374.

Lee, Y., Pinedo, M. (1997). Scheduling jobs on parallel machines with sequence dependent setup times. European Journal of Operational Research, Vol. 100, pp. 464-474.

Lejeune, M.A. (2006). A variable neighborhood decomposition search method for supply chain management planning problems. European Journal of Operational Research, Vol. 175 (2), pp. 959-976.

Li, D. C., She, I. S. (1994). Using unsupervised learning technologies to induce scheduling knowledge for FMSs. Int. J. Prod. Res., Vol. 32(9), pp. 2187-2199.

Li, J., Li, W., Karimi, I.A., Srinivasan, R. (2007). Improving the robustness and efficiency of crude scheduling algorithms. AIChE Journal, Vol. 53 (10), pp. 2659-2680.

Li, K. P., Ganesan, V. K.,  Sivakumar, A. I. (2005). Synchronized scheduling of assembly and multi-destination air transportation in a consumer electronicssupply chain. International Journal of Production Research, Vol. 43, pp. 2671-2685.

Li, K. P., Ganesan, V. K.,  Sivakumar, A. I. (2006). Scheduling of single stage assembly with air transportation in a consumer electronic supply chain. Computers and Industrial Engineering, Vol. 51, pp. 264-278.

Li, K. P., Sivakumar, A. I., Ganesan, V. K. (2008). Complexities and algorithms for synchronized scheduling of parallel machine assembly and air transportation in consumer electronic supply chain. European Journal of Operational Research, Vol. 187, pp. 442-455.

Li, K. P., Sivakumar, A. I., Mathirajan, M., Ganesan, V. K. (2004). Solution methodology for synchronizing assembly manufacturing and air transportation of consumer electronics supply chain. International Journal of Business, Vol. 9, pp. 361-380.

Li, k., Appa Iyer, S., Fu, Q., Jin, X. (2007). A Case Study for Synchronized Scheduling of manufacturing and air transportation in Consumer Electronics Supply Chain, Proceedings of the 2007 IEEE IEEM.

Li, Q., Liang, L., Qiao, W. (2011). A Hybrid Robust Scheduling for Single Machine Subject to Random Machine Breakdown. Fourth International Workshop on Advanced Computational Intelligence Wuhan, Hubei, China.

Lin, C.H., Liao, C.J. (2003). Makespan minimization subject to flowtime optimality on identical parallel machines, Computers and Operations Research, Vol. 31, pp. 1655-1666.

Liouane, N., Saad, I., Hammadi, S., Borne, P. (2007). Ant systems & Local Search Optimization for flexible Job Shop Scheduling Production, International Journal of Computers, Communications & Control Vol. II (2007), No. 2, pp. 174-184.

Logendran, R., McDonell, B., Smucker, B. (2007). Scheduling unrelated parallel machines with sequence-dependent setups. Computers & Operations Research, Vol. 34, pp. 3420-3438.

Luh, P., Feng, W. (2003). From Manufacturing Scheduling to Supply Chain Coordination: The Control of Complexity and Uncertainty, The Fourth International Conference on Control and Automation (ICCA'03), 10-12 June 2003, Montreal, Canada.

Ma Fei，Wu Meng-Na, Sun Bao-Feng，Yang Hua. (2009). The Coordination of Production and Distribution Scheduling in Mass Customization, 2009 International Conference on Management Science & Engineering (16th) September 14-16, Moscow, Russia.

Majazi, V., Mohammadi, G. (2012). Two meta-heuristic algorithms for solving multi-objective flexible job-shop scheduling with parallel machine and maintenance constraints, Computers and Mathematics with Applications.

Mansouri, S. (2006). A simulated annealing approach to a bi-criteria sequencing problem in a two-stage supply chain, Computers & Industrial Engineering, Vol. 50, pp. 105-119.

Martí, R. (2003) (a). Procedimientos metaheurísticos en optimización combinatoria. Matemátiques, Vol. 1.

Martí, R. (2003). Algoritmos heurísticos en optimización combinatoria. Universidad de Valencia, Departamento de Estadística e Investigación Operativa.

Mastrolilli, M., Gambardella, L. M. (2000). Effective neighborhood functions for the flexible job shop problem. Journal of Scheduling, Vol. 3(1), pp. 3-20.

Mazzini, R., Armentano, V. (2001). A heuristic for single machine scheduling with early and tardy costs, European Journal of Operational Research, Vol. 128, pp. 129-146.

Mendes, A., Muller, F., Franca P., Moscato, P. (2002). Comparing meta-heuristic approaches for parallel machine scheduling problems. Faculdade de Engenharia Elétrica e de Computação Universidade Estadual de Campinas - UNICAMP C.P. Campinas - SP - Brazil.

Mendes, A., Muller, F., Franca P., Moscato, P. (2002). Comparing meta-heuristic approaches for parallel machine scheduling problems. Faculdade de Engenharia Elétrica e de Computação Universidade Estadual de Campinas - UNICAMP C.P. Campinas - SP - Brazil.

Mezmaz, M., Melab, N., Talbi, E.G. (2006). A Parallel Exact Hybrid Approach for Solving Multi-Objective Problems on the Computational Grid, Laboratoire d’Informatique Fondamentale de Lille UMR CNRS 8022, INRIA Futurs - DOLPHIN Project, IEEE.

Monahan, J. P. (1984). A Quantity Discount Pricing Model to Increase Vendor Profits, Management Science, Vol. 30(6), pp. 720-726.

Monch, L., Balasubramanian, H., Fowler, J., Pfund, M. (2005). Heuristic scheduling of jobs on parallel batch machines with incompatible job families and unequal ready times, Computers & Operations Research, Vol. 32, pp. 2731-2750.

Moon, C., Kim, J., Hur, S. (2002). Integrated process planning and scheduling with minimizing total tardiness in multi-plants supply chain. Computers & Industrial Engineering, Vol. 41, pp. 331-349.

Moon-Won Park, Yeong-Dae Kim. (1997). Search Heuristics for a Parallel Machine scheduling Problem with Ready Times and Due Dates, Computers ind. Engng, Vol. 33, pp. 793-796.

Naderi, B., Fatemi Ghomi, S., Aminnayeri, M. (2010). A high performing metaheuristic for job shop scheduling with sequence-dependent setup times, Applied Soft Computing, Vol. 10, pp. 703-710.

Naso, D., Surico, M., Turchiano, B., Kaymak, U. (2007). Genetic algorithms for supply-chain scheduling: a case study in the distribution of ready-mixed concrete. European Journal of Operational Research, Vol. 177 (3), pp. 2069-2099.

Nash, J. (1050) “The bargaining problem. Econometrica”, Vol. 18, pp. 155-162.

Nowicki, E., Smutncki, C. (1996). A fast Tabu search algorithm for the permutation flow-shop problem. European Journal Operational Research, Vol. 91, pp. 160-175.

Nowicki, E., Smutncki, C. (1996). A fast Tabu search algorithm for the permutation flow-shop problem. European Journal Operational Research, Vol. 91, pp. 160-175.

Ogbu, F.A., Smith, D.K. (1990). The application of the simulated annealing algorithm to the solution of the n/m/cmax flow shop problem. Computers & Operations Research, Vol. 17 (3), pp. 243-253.

Ogbu, F.A., Smith, D.K. (1991). Simulated annealing for the permutation flow-shop problem. Omega, Vol. 19, pp. 64-67.

Ortiz, M., Neira, D., Jimenez, G., Hernández, H. (2016). Solving flexible Job-Shop Scheduling Problem with Transfer barches, Set up times and multiple resources in Apparel Industry. Lecture Notes in Computer Science, Vol. 9713, pp. 47-58

Osman, I. H., Kelly, J. P. (1996). Meta-Heuristics: Theory and Applications. 39 Kluwer Academic Publishers.

Osman, I.H., Potts, C.N. (1989). Simulated annealing for permutation flow-shop scheduling. Omega 17 (6), 551-557.

Ovallos-Gazabón, D., Villalobos-Toro, B., De la Hz-Escorcia, S., Maldonado-Pérez, D. (2016). Gamificación para la gestión de la innovación a nivel organizacional. Una revisión del estado del arte. Revista Espacios, Vol. 37(8), pp. 2.

Ow, P.S., Morton, T.E. (1989). The single machine early/tardy problem. Management Science, Vol. 35, pp. 177-191.

Palmer, D., (1965). Sequencing jobs through a multi-stage process in the minimum total time-a quick method of obtaining a near optimum. Operations Research Quarterly, Vol. 16, pp. 101-107.

Parviz Fattahi, Mohammad Saidi Mehrabad, Mir B. Aryanezhad (2006). An Algorithm for multi-objective job shop scheduling problem, Journal of Industrial Engineering International, Islamic Azad University, South Tehran Branch, Vol. 2, No. 3, pp. 43-53.

Pauli, J. (1995). A hierarchical approach for the FMS schduling problem. European Journal of Operational Research, Vol. 86(1), pp. 32-42.

Piersma, N., Van Dijk, W. (1996). A Local Search Heuristic for Unrelated Parallel Machine Scheduling with Efficient Neighborhood Search, Mathl. Comput. Modelling, Vol. 24, No. 9, pp. 11-19.

Pinedo, M. (2002). Scheduling: Theory, Algorithms and Systems. Prentice Hall, Englewood Cliffs, NJ.

Ping, Y., Minghai, J. (2011). An Improved PSO Search Method for the Job Shop Scheduling Problem, Chinese Control and Decision Conference (CCDC).

Ping, Y., Minghai, J. (2011). An Improved PSO Search Method for the Job Shop Scheduling Problem, IEEE.

Quadt, D., Kuhn, H. (2007). Batch scheduling of jobs with identical process times on flexible flow lines. International Journal of Production Economics, Vol. 105, pp. 385-401.

R. Zhang, Wu, C. (2006). A hybrid immune simulated annealing algorithm for the job shop scheduling problem, Applied Soft Computing, Vol. 10, no. 1, pp. 79-89.

Reeves, C. (1993). Improving the efficiency of tabu search for machine sequencing problems, Journal of the operational research society, Vol. 44, pp. 375-382.

Reeves, C. (1995). Heuristics for scheduling a single machine subject to unequal job release times, European Journal of Operational Research, Vol. 80, pp. 397-403.

Reeves, C.R. (1995). A genetic algorithm for flow shop sequencing. Computers and Operations Research, Vol. 22 (1), pp. 5-13.

Restrepo, J. (2010). Application the palmer´s heuristic for sequencing n jobs trough m machines: a study case. Scientia et Technica Año XVII, No 46. Universidad Tecnológica de Pereira.

Rivera, J.C. (2007). Estrategias heurísticas adaptativas para la solución del problema de programación de proyectos con recursos limitados (rcpsp). Universidad Nacional de Colombia - Sede Medellín.

Ruiz-Torres, A.J., Ho, J.C., Lopez, F.J. (2006). Generating Pareto schedules with outsource and internal parallel resources. International Journal of Production Economics, Vol. 103 (2), pp. 810-825.

Saharidis, G. (2011). Supply Chain Optimization: Centralized vs Decentralized Planning and Scheduling. University of Thessaly, Department of Mechanical Engineering.

Sait  Sadiq, M., Youssef, H. (1999). Iterative Computer Algorithms with Applications in Engineering. Solving Combinatorial Optimization Problems. IEEE computer Society.

Salas, K., Acosta Villa, C., Sandoval Cortés, L., Pacheco, G., Mercado Caruso, N. (2016). Análisis estratégico de cluster de servicios logísticos. Revista Espacios, Vol. 37 (28), pp. 5.

Salas Navarro, K., Chedid, J.A., Caruso, N.M., Sana, S.S. (2016). An Inventory model of three-layer supply chain of Wood and furniture industry in the Caribbean region of Colombia. International Journal of Systems Science: Operations and Logistics, Vol 4, pp. 1-18.

Sana, S.S., Chedid, J.A., Navarro, K.S. (2014). A three layer supply chain model with multiple suppliers, manufacturers and retailers for multiple items, Applied Mathematics and Computation, Vol. 229, pp. 139-150

Sarmiento, A. M., Nagi, R. (1999). A review of integrated analysis of production-distribution systems. IIE Trans, Vol. 31, pp. 1061-1074.

Selvarajah, E., Steiner, G. (2005). Batch scheduling in a two-level supply chain A focus on the supplier. European Journal of Operational Research.

Sevaux, M., Orensen, K. (2005). VNS/TS for a parallel machine scheduling problem, MEC-VNS: 18th Mini Euro Conference on VNS.

Sevkli, M., Aydin, M. (2006). Variable Neighbourhood Search for Job Shop Scheduling Problems, Journal Of Software, Vol. 1, No. 2.

Shahvari, O., Salmasi, N., Logendran, R. (2009). A Meta-Heuristic Algorithm for Flexible Flow Shop Sequence Dependent Group Scheduling Problem, Proceedings of the 2009 International Conference on Value Chain Sustainability.

Shapley, L. (1953) Avalue for n-person games in Kuhn, W., Tucker, W., editors, “Contributions to the Theory of Games II”, Princeton University Press, Princeton, pp. 307-317.

Shi, D., He, J., Wang, L. (2009). Job Shop Scheduling Problem with an Novel Particle Swarm Optimization based on Tabu Search, International Conference on Artificial Intelligence and Computational Intelligence.

Smith, R. G. (1980). The Contract Net Protocol: High-level Communication and Control in the Distributed Problem Solver, IEEE Transactions on Computers, Vol. C-29, No. 12, pp. 1104-1113.

Sortrakul, N., Nachtmann, H.L., Cassady, C.R. (2005). Genetic algorithms for integrated preventive maintenance planning and production scheduling for a single machine, Computers in Industry, Vol. 56, pp. 161-168.

Stewart, I., Fenn, P. (2006). Strategy: the motivation for innovation. Construction Innovation, Vol. 6, pp, 173-185.

Stutzle, T. (1998). An ant approach to the flow shop problem. In: Proceedings of the Sixth European Congress on Intelligent Techniques and Soft Computing, Aachen, Germany, Verlag Mainz, pp. 1560-1564.

Suresh, V., Chaudhuri, D. (1996). Bicriteria scheduling problem for unrelated parallel machines” Computers & Industrial Engineering, Vol. 30, pp. 77-82.

Taillard, E. (1990). Some efficient heuristic methods for the flow shop sequencing problem. European Journal of Operational Research, Vol. 47, pp. 65-74.

Tang, J., Zhang, G., Lin, B. (2010). Hybrid Genetic Algorithm for Flow Shop Scheduling Problem, International Conference on Intelligent Computation Technology and Automation.

Tang, L., Wang, X. (2010). An Improved Particle Swarm Optimization Algorithm for the Hybrid Flow-shop Scheduling to Minimize Total Weighted Completion Time in Process Industry. IEEE transactions on control systems technology, Vol. 18, N°. 6.

Tavakkoli-Moghaddama, R., Safaei, N., Sassani, F. (2009). A memetic algorithm for the flexible flow line scheduling problem with processor blocking, Computers & Operations Research, Vol. 36, pp. 402-414.

Thomas, D. J., Griffin, P. M. (1996). Coordinated supply chain management. European Journal of Operational Research, Vol. 94, pp. 1-15.

Toloie, A., Ahmad, S. (2011). Scheduling in flexible job-shop manufacturing system by improved tabu search, African Journal of Business Management, Vol. 5(12), pp. 4863-4872.

Torabi, S. A., Fatemi Ghomi, S. M. T., Karimi, B. (2005). A hybrid genetic algorithm for the finite horizon economic lot and delivery scheduling in supply chains. European Journal of Operational Research.

Torabi, S., Jenabi, M., Mansouri, A. (2008). Hybrid Genetic Algorithms for the Lot Production and Delivery Scheduling Problem in a Two-Echelon Supply Chain, A. Fink and F. Rothlauf (Eds.): Advances in Computational Intelligence, SCI 144, pp. 253-275.

Trentesaux, D. Distributed control of production systems. Engineering Applications of Artificial Intelligence, Vol. 22 (7), pp. 971-978.

Tseng M M, Jiao (1996). Design for mass customization?. Annals of the CIRP, Vol. 45(1), pp. 153-6.

Valente, J. (2008). Beam search heuristics for the single machine early/tardy scheduling problem with no machine idle time, Computers & Industrial Engineering, Vol. 55, pp. 663-675.

Valente, J., Alves, R. (2007). Heuristics for the single machine scheduling problem with quadratic earliness and tardiness penalties, Computers & Operations Research, Vol. 35, pp. 3696-3713.

Valente, J., Schaller, J. (2011). Dispatching heuristics for the single machine weighted quadratic tardiness scheduling problema, Computers & Operations Research, Vol. 39, pp. 2223-2231.

Van Den Heever, S.A., Grossmann, I.E. (2003). A strategy for the integration of production planning and reactive scheduling in the optimization of a hydrogen supply network. Computers and Chemical Engineering, Vol. 27 (12), pp. 1813-1839.

Varadharajan, T.K., Rajendran, C. (2005). Amulti-objective simulated-annealing algorithm for scheduling in flowshop to minimize the makespan and total flowtime of jobs”. European Journal of Operational Research, Vol. 167(3), pp. 772-795.

Velez, M., López, J. (2011). A variable neighborhood search algorithm to minimize the total weighted tardiness on a batch processing machine, 1PDepartamento de Ingeniería de Production, Universidad EAFIT, Ingeniería Industrial-Año. Vol. 10, Nº1: pp. 5-18, Medellín, Colombia.

Verderame, P.M., Elia, J.A., Li, J., Floudas, C.A. (2010). Planning and scheduling under uncertainty: A revire across multiple sectors. Industrial Engineering Chemistry Research, Vol. 49 (9), pp. 3993-4017.

Vergara, F. E., Khouja, M., Mickalewicz, Z. (2002). An evolutionary algorithm for optimizing material flow in supply chains. Computers & Industrial Engineering, Vol. 43, pp. 407-421.

Vianna, Y., Vianna, M., Medina, B., & Tanaka, S. (2014). Gamificacion, Inc - Recreating Companies Through Games. MJV Press.

Wang Xu, Jia Yan-Min, Yu Tian-Lai (2008). Research on Dynamic Scheduling Operation Method in Supply Chain Based on Ant Colony Optimization, The IEEE International Conference on Industrial Informatics, DCC, Daejeon, Korea.

Wang, L., Zheng, D. (2001). An effective hybrid optimization strategy for job-shop scheduling problems, Computers & Operations Research, Vol. 28, pp. 585-596.

Wang, W., Cheng, T. C. E. (2009). Production Scheduling with Supply and Delivery Considerations to Minimize the Makespan, School of Economics and Management, Nanjing University of Science and Technology, Nanjing, China Department of Logistics, The Hong Kong Polytechnic University, Hung Hom, Kowloon, Hong Kong.

Witt, A., Voß, S. (2007). Job Shop Scheduling with Buffer Constraints and Jobs Consuming Variable Buffer Space, W. Dangelmaier et al. (Eds.), LNBIP, Vol. 46, pp. 295-307.

Woeginger, G.J. (1994). Heuristics for parallel machine scheduling with delivery times, Acta Informatica, Vol. 31, pp. 503-512.

Xu, D., Yin, Y. (2011). On single-machine scheduling with flexible maintenance activities. Int J Adv Manuf Technol. Vol. 56, pp. 1139-1145.

Yamada, T., Reeves, C. (1997). Permutation flowshop scheduling by genetic local search. Proceedings of the 2nd IEE/IEEE International Conference on Genetic Algorithms in Engineering Systems (GALESIA ‘97), London, UK:IEE, pp. 232-238.

Yun-Chia Liang, Yu-Ming Hsiao, Chia-YunTien (2011). Metaheuristics for drilling operation scheduling in Taiwan PCB industries, Int. J. Production Economics, Department of Industrial Engineering and Management, Yuan Ze University.

Yun-Chia Liang, Yu-Ming Hsiao,Chia-Yun Tien. (2012). Metaheuristics for drilling operation scheduling in Taiwan PCB industries, SciVerse ScienceDirect.

Zhang, C. Y., Li, P. G., Rao, Y. Q., Guan, Z. L. (2008). A very fast TS/SA algorithm for the job shop scheduling problem, Computers & Operations Research, Vol. 35, no. 1, pp. 282-294.

Zhi-Long Chen. (2010). Integrated Production and Outbound Distribution Scheduling: Review and Extensions, Operations Research, Vol. 58, No. 1, pp. 130-148.

Zhong, W., Dosa, G., Tan, Z. (2007). On the machine scheduling problem with job delivery coordination. European Journal of Operational Research, Vol. 182 (3), pp. 1057-1072.

Zobolas, G.I., Tarantilis, C.D., Ioannou, G. (2009). Minimizing makespan in permutation flow shop scheduling problems using a hybrid metaheuristic algorithm, Computers & Operations Research, Vol. 36, pp. 1249-1267.

Zribi, N., El Kamel, A., Borne, P. (2006). Total Tardiness in a Flexible Job-shop, IMACS Multiconference on Computational Engineering in Systems Applications (CESA), October 4-6, 2006, Beijing, China.

1. Ingeniero Industrial, Magíster en Ingeniería Industrial, Candidato a Doctor en Ingeniería Industrial de la Universidad del Norte. Profesor Tiempo Completo de la Universidad Tecnológica de Bolívar. Cartagena de Indias, Colombia. jacevedo@unitecnologica.edu.co

2. Ingeniera Industrial, Magíster en Ingeniería, Estudiante de Doctorado en Ingeniería de la Universidad Pontificia Bolivariana. Profesor Tiempo Completo de la Universidad de la Costa. Barranquilla, Colombia. ksalas2@cuc.edu.co

3. Ingeniero Industrial, Magíster en Ingeniería. Profesor Tiempo Completo de la Universidad Tecnológica de Bolívar. Cartagena de Indias, Colombia. hospina@unitecnologica.edu.co

4. Ingeniero Industrial, Especialista en Logística Empresarial, Magíster en Ingeniería Industrial, Magíster en Comercio Internacional, Doctor en Ingeniería Industrial. Profesor Tiempo Completo de la Universidad del Norte. Barranquilla, Colombia. asantand@uninorte.edu.co