ISSN 0798 1015

Vol. 38 (Nº 24) Año 2017. Pág. 33

Influencia de un parque en los cánones de arrendamiento de vivienda en Laureles en 2015: Una aplicación de regresión de geográficamente ponderada en el contexto de precios hedónicos

Influence of a park in the rents of housing in Laureles in 2015: An application of geographically weighted regression in the context of hedonic pricing

Jorge Enrique AGUDELO Torres 1; Diego Fernando MARTÍNEZ Montoya 2; Oscar Alonso OSPINA Espinoza 3

Recibido: 24/11/2016 • Aprobado: 14/01/2017

Contenido

1. Introducción

2. Metodología

3. Caso de estudio

4. Resultados

5. Conclusiones

Referencias

1. Introducción

A partir de la década del setenta del siglo pasado y gracias a la “Nueva aproximación de la teoría del consumidor” propuesta por Lancaster (1966), los trabajos relacionados con el sector inmobiliario comenzaron a asociar el precio de los bienes inmuebles con sus características, como lo hizo posteriormente Rosen (1974) quien se convirtió en un pionero de esta línea.

En las décadas siguientes, autores como Can (1992), Sheppard (1999), Basu y Thibodeau (1998) se preocuparon por clasificar los atributos de los inmuebles, con el fin de evitar sesgos de especificación provocados por la omisión de variables relevantes en los modelos. Sin embargo, la utilización de la metodología econométrica tradicional en este tipo de análisis, permitió la aparición de problemas relacionados con la asociación espacial de los datos del mercado inmobiliario y con la heterogeneidad espacial, según la cual los parámetros obtenidos a partir de datos espaciales varían en el espacio. Anselin (1988).

Fotheringham, Brundson y Charlton (2002) propusieron una técnica denominada regresión geográficamente ponderada (GWR), que permite la generación de múltiples ecuaciones, con múltiples coeficientes, de manera que cada característica posee un parámetro cuya estimación varía en función de la ubicación del inmueble en el espacio. De esta manera los problemas asociados a la heterogeneidad espacial y a la asociación espacial de los datos, son minimizados. Por ejemplo, gracias a la técnica GWR, en el mercado inmobiliario es posible obtener diferentes estimaciones de un parámetro relacionado con el valor de un parqueadero en distintas zonas de la ciudad, mientras que con la econometría tradicional sólo puede obtenerse un valor promedio de todos los parqueaderos, dificultando el análisis puntual para una zona específica.

A partir de la técnica GWR se han publicado varios estudios relacionados con el mercado inmobiliario. Yu (2004) estudió el precio de las viviendas en Milwaukee y encontró que la edad de construcción de las viviendas reduce su valor en la mayoría de los casos; sin embargo, éste puede incrementarse como consecuencia del valor histórico de las mismas. Bitter, Mulligan y Dall´erba (2007) especificaron un modelo de precios hedónicos para las viviendas de Tucson, Arizona, obteniendo como resultado un mayor poder de predicción del modelo GWR, frente a los modelos econométricos tradicionales. Lu, Charlton y Fotheringham (2011) emplearon modelos GWR para estudiar los precios de las viviendas en Londres, incluyendo distancias euclidianas y no euclidianas en sus modelos, obteniendo que estas últimas mejoran sus estimaciones levemente, al compararse con las primeras.

El empleo de la técnica GWR en el estudio del mercado inmobiliario ha sido poco, en particular en Colombia, ya que la obtención de datos es complicada, como consecuencia de la situación de seguridad del país, entre otras razones, lo que induce a los individuos a ocultar información relacionada con su patrimonio.

En este trabajo se utilizan regresiones geográficamente ponderadas para buscar evidencia empírica acerca de la influencia del parque, en los cánones de arrendamiento de las viviendas ubicadas en el barrio, de manera que dicha cercanía constituye una externalidad positiva para las viviendas de la zona.

Después de esta introducción, en este artículo se presenta la metodología de regresión geográficamente ponderada. Luego se explican las características del caso de estudio y de los datos utilizados; finalmente se presentan los resultados, su interpretación, y algunas conclusiones relevantes.

2. Metodología

En los modelos econométricos tradicionales usualmente se considera una regresión del tipo:

O en forma matricial:

En donde:

y: Vector de dimensión de n observaciones de la variable endógena.

X: Matriz de dimensión, donde k-1 es la cantidad de variables exógenas del modelo.

b: Vector de dimensión de parámetros de las variables exógenas.

U: Vector de dimensión de perturbaciones aleatorias ruido blanco.

Utilizando el método de mínimos cuadrados ordinarios o el de máxima verosimilitud se puede obtener un estimador adecuado del vector de parámetros b:

Sin embargo, para variables que presentan el fenómeno de dependencia espacial debe utilizarse otro tipo de modelos llamados modelos econométricos espaciales, entre los cuales se encuentran los obtenidos por medio de regresiones geográficamente ponderadas, las cuales permiten estimar modelos locales para cada una de las observaciones:

Donde (ui, vi) representan las coordenadas que describen la ubicación geográfica de la observación.

Mediante métodos de estimación tales como el de máxima verosimilitud o el de mínimos cuadrados ordinarios es posible estimar el vector de parámetros:

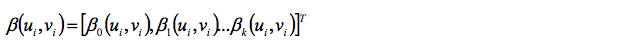
Como se describe a continuación.

En el modelo lineal general 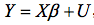,  premultiplicando por una matriz de ponderaciones Tno singular, se obtiene:

3. Caso de estudio

3.1. Contexto

Laureles es un barrio de estrato medio alto ubicado en la comuna Laureles Estadio, situada en el centro occidente de la ciudad de Medellín, Colombia, que según datos de la alcaldía de la ciudad para 2.010 contaba con 5.683 viviendas, de las cuales el 97% estaban catalogadas como estrato cinco y el restante porcentaje como estrato cuatro. Los datos más recientes indican que en la comuna 11, en donde se ubica el barrio, habitan 41.376 hogares, de los cuales  12.219 ocupan una vivienda en arriendo o subarriendo.

La estructura urbana del barrio es bastante heterogénea y está conformada principalmente por viviendas multifamiliares y en menor medida por viviendas bifamiliares y trifamiliares antiguas. Con el paso del tiempo por estar ubicado en la zona central de la ciudad, el barrio ha desarrollado una cantidad importante de comercio en los primeros niveles de las edificaciones así como de edificios de oficinas. El barrio limita al norte con los barrios Lorena y Bolivariana, al occidente con el barrio Las Acacias, al sur con la comuna Belén y al oriente con el barrio Bolivariana y con la Universidad Pontificia Bolivariana.

El barrio Laureles cuenta dentro de su entorno con la avenida Bolivariana que permite una buena movilidad vehicular en el occidente de la ciudad, adicionalmente el barrio limita con la avenida 33 que es una de las vías más transitadas de la ciudad y permite la conexión del occidente con el centro de la ciudad. Laureles cuenta una buena dotación de servicios de estrato medio alto, entre los cuales se incluyen colegios privados, universidades,  zonas verdes, zonas deportivas, iglesias y zonas comerciales como la ubicada alrededor del segundo parque de Laureles, lo que favorece la demanda de vivienda para compra y alquiler, de forma que según la Lonja de Propiedad Raíz de Medellín y Antioquia, es una de las zonas en las que más rápidamente se alquila o vende una vivienda usada en la ciudad, con un promedio de sesenta días.

La motivación del estudio radica en presentar un modelo de regresión geográficamente ponderada para el mercado de arrendamientos del barrio Laureles, que permita predecir el número de días que va tomarle a un apartamento arrendarse dadas las características básicas del mismo como su área o distancia al parque principal del barrio.

3.2. Datos utilizados

Para desarrollar  el estudio se emplearon datos correspondientes a 140 cánones de arrendamiento de viviendas que se alquilaron durante 2015 en el barrio Laureles. La muestra representa el 2.46% del total de viviendas del barrio, aunque no todas las viviendas del barrio estaban alquiladas y tampoco todas estaban en oferta de arrendamiento durante 2015.

Los datos utilizados en el trabajo fueron aportados por la Lonja de Propiedad Raíz de Medellín y Antioquia y fueron obtenidos a partir de un recorrido de campo que realiza la empresa en los principales barrios de la ciudad, dado que por la difícil situación de seguridad del país ni los propietarios ni los arrendatarios dan a conocer estas cifras. La metodología de recolección de los datos está basada en un recorrido de campo que se hace mensualmente por todos los barrios, detectando los anuncios de ofertas de venta y arrendamiento de vivienda. Una vez se tiene el dato, se contacta telefónicamente a la empresa o persona que ofrece el inmueble y se indaga por aspectos relacionados con el inmueble en oferta. Cada mes se verifica si el inmueble continúa en oferta o si ya ha sido comercializado. Esta metodología permite obtener datos primarios de buena calidad para realizar un seguimiento al mercado inmobiliario de la ciudad.

Grafico 1. Plano de la zona

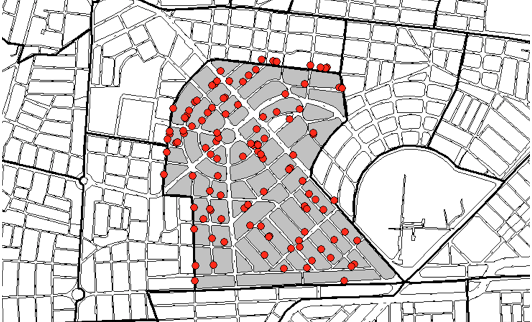
Fuente: elaboración propia con base en el software Mapinfo.

En el Gráfico 1 se observa el plano de la zona, resaltando en un color más oscuro las manzanas que hacen parte del barrio Laureles. Cada punto representa un dato de un inmueble arrendado.

Las estadísticas descriptivas de la tabla 1 muestran la diversidad de las viviendas en arrendamiento de la zona, que tienen cánones que oscilan entre $450.000 mensuales para apartamentos de 25 metros cuadrados sin parqueadero y $4.000.000 mensuales para una vivienda de 346 metros cuadrados con dos parqueaderos.

Tabla 1. Descripción de la muestra de viviendas.

Fuente: elaboración propia.

3.3. Definición de variables

Las variables utilizadas en la modelación son las siguientes:

Canon: Es el valor del arrendamiento del inmueble en pesos colombianos.

Piso: Corresponde al nivel del edificio en que se encuentra ubicada la vivienda. Mientras mayor es el piso mayor es el canon de arrendamiento

Área: Se refiere al número de metros cuadrados con que cuenta la vivienda. Mientras mayor es el área de la vivienda mayor es el canon de arrendamiento.

Garajes: Hace referencia al número de parqueaderos con que cuenta una vivienda. Mientras más garajes tenga la vivienda mayor es el canon de arrendamiento en el mercado más posibilidades tiene de alquilarse el inmueble.

Distancia: Esta variable hace referencia a la distancia lineal que hay entre la vivienda y el  parque de Laureles. Habitualmente los hogares prefieren ubicarse cerca del segundo parque. Se espera que mientras más cercanas sean las viviendas al parque mayores sean los cánones de arrendamiento.

A continuación se presentan los resultados obtenidos empleando la metodología de regresiones ponderadas geográficamente, a partir de las cuales se realizan comparaciones y se obtienen las conclusiones.

4. Resultados

Al emplear datos espaciales es necesario verificar la existencia de autocorrelación espacial, para lo cual se utiliza el estadístico conocido como I de Moran. Como se presenta en el Gráfico 2, con un valor p de 0.001, es posible afirmar con un 95% de confianza, que no existe evidencia de la existencia de no autocorrelación espacial de los datos; es decir, deben tenerse en cuenta los efectos espaciales de los datos para realizar el análisis. Para ellos se emplea una matriz de pesos espaciales W, generada con el método K-Nearest neighborhood igual a 4, ya que se asume que cada vivienda considerada tiene cuatro viviendas vecinas, en la muestra, con características similares a ella.

Gráfico 2. Valor p y función de densidad de probabilidad

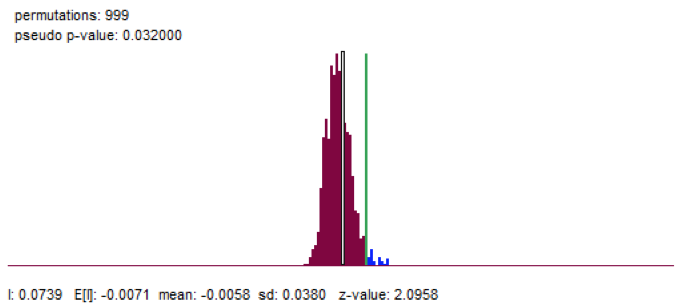
Fuente: elaboración propia con base en el software GeoDa.

Una vez verificada la existencia relaciones espaciales entre las variables utilizadas, se empleó el programa GWR3 para estimar una regresión ponderada geográficamente. Luego de siete iteraciones, se obtuvo el siguiente criterio de minimización de Akaike:

Tabla 2. Ancho de Banda

A partir del modelo de regresión geográficamente ponderada se especificaron 140 ecuaciones, todas con coeficientes de determinación que oscilan entre el 80% y el 89%.

Grafico 3. Resultados

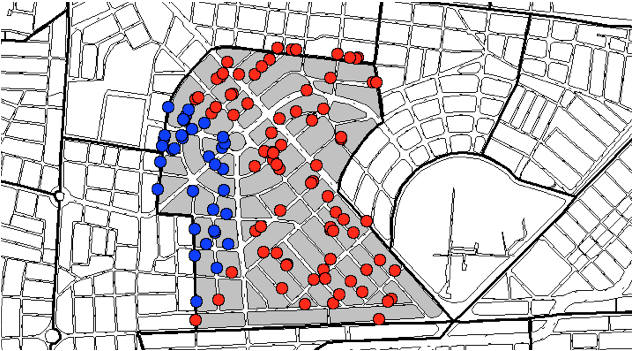
Fuente: elaboración propia con base en el software Mapinfo.

En el gráfico 3 se representan con color rojo aquellas viviendas que muestran coeficientes negativos de la variable distancia, que corresponde al trayecto medido en metros lineales entre la ubicación de la vivienda y el segundo parque de Laureles. El 70% de las viviendas analizadas, presentan un coeficiente negativo de la variable distancia indicando – ceteris paribus - que mientras más alejadas se encuentren del parque, menores son sus cánones de arrendamiento. Sin embargo, es particularmente llamativo que las viviendas ubicadas más al occidente del barrio y cruzando la carrera 76 presentan coeficientes positivos para la variable distancia, posiblemente porque el mercado reconoce que estar más lejos del parque, pero más cerca del mall Laureles y del complejo comercial VIVA Laureles, es considerado beneficioso y por ende pueden cobrarse cánones de arrendamientos un poco mayores.

Comparando los resultados del modelo GWR  con un modelo OLS clásico, se observa la mayor capacidad predictiva de GWR, como se deduce de las predicciones obtenidas en una muestra de cinco datos: 

Resultados que son consistentes con la mayor capacidad predictiva y de ajuste que usualmente tienen los modelos de la familia GWR.

5. Conclusiones

En este trabajo se utilizaron regresiones geográficamente ponderadas para analizar la influencia que tiene el parque de Laureles en los cánones de arrendamiento del barrio. Este tipo de modelos se consolidan como los más apropiados para analizar la influencia que tienen sobre los cánones arrendamiento de las viviendas elementos de infraestructura pública como vías, parques y estaciones de sistemas masivos de transporte.

La variable correspondiente a la distancia entre la vivienda y el parque resultó ser significativa y muestra una influencia positiva en los cánones de arrendamiento del barrio, con excepción de aquellas viviendas ubicadas al occidente del barrio y cercanas a zonas comerciales consolidadas en donde la influencia del parque muestra ser menor.

Futuros trabajos relacionados con el tema, se enfocarán en la influencia que tiene sobre los valores de venta de un inmueble la cercanía a elementos de infraestructura como vías, estaciones de sistemas de transporte masivo o aeropuertos.

Referencias

AGUDELO, J. E.; Agudelo, G. A.; Franco, L. C.; Franco, L. E. (2015). Efecto de un estadio deportivo en los precios de arrendamiento de viviendas: una aplicación de regresión ponderada geográficamente (GWR). Ecos de Economía, 19(40), 66-80.

ALCALDÍA DE MEDELLÍN. (2010). Viviendas residenciales estratificadas por comuna y barrio, según estrato. Recuperado de: https://www.medellin.gov.co

ANAS, A. (1990). Taste heterogeneity and urban spatial structure: The logit model and monocentric theory reconciled. Journal of Urban Economics, 28(3), 31 8-335.

AUGUSTIN, N. H.; Cummins, R. P.; French, D. D. (2001). Exploring spatial vegetation dynamics using logistic regression and a multinomial logit model. Journal of Applied Ecology, 38(5), 991-1006.

AUTANT-BERNARD, C. (2006). Where do firms choose to locate their R&D? A spatial conditional logit analysis on french data. European Planning Studies, 14(9), 1187-1208.

BHAT, C. R.; Sener, I. N. (2009). A copula-based closed-form binary logit choice model for accommodating spatial correlation across observational units. Journal of Geographical Systems, 11(3), 243-272.

BASU, S.; Thibodeau, TG. (1998). Analysis of spatial autocorrelation in house prices. The Journal of Real Estate Finance and Economics, 17:61-85.

BEATY, J. (1952). Rental real estate often a good investment. Med Econ. 5(6): 93 – 94.

BITTER, C.; Mulligan, G.; Dall'erba, S. (2007). Incorporating spatial variation in housing attribute prices: a comparison of geographically weighted regression and the spatial expansion method. Journal of Geographical Systems, 9(1): 7-27.

CARL, G., & Kühn, I. (2007). Analyzing spatial autocorrelation in species distributions using gaussian and logit models. Ecological Modelling, 207(2-4), 159-170.

DEWEY, L.; DeTuro, P. (1950). Should I invest in real estate? Med Econ. 28(3): 85 – 93.

LANCASTER, K. (1966). A new approach to consumer theory. Journal of Political Economy. 74(1):132 – 157.

LEE, H. L.; Cohen, M. A. (1985). A multinomial logit model for the spatial distribution of hospital utilization. Journal of Business and Economic Statistics, 3(2), 159-168.

LI, M.; Wu, J.; Deng, X. (2013). Identifying drivers of land use change in china: A spatial multinomial logit model analysis. Land Economics, 89(4), 632-654.

LU, B.; Charlton, M.; Fotheringham, A. S. (2011) Geographically Weighted Regression Using a Non-Euclidean Distance Metric with a Study on London House Price Data. Procedia Environmental Sciences, 7, 92-97.

ROSEN, S. (1974). Hedonic prices and implicit markets: product differentiation and pure competition. Journal of Political Economy. 82: 34 – 55.

SELIM, H. (2009). Determinants of house prices in Turkey: Hedonic regression. Expert Systems with Applications, 36 (2), pp. 2843–2845.

SHEPPARD, S. (1999). Hedonic analysis of housing markets. En: P.C. Cheshire, E.S. Mills (Eds.), Handbook of regional and Urban Economics, vol. 3, pp. 1595–1635 North Holland, Amsterdam.

VENEGAS-MARTÍNEZ, F.; Agudelo, G.A.; Franco, L.C.; Franco, L.E. (2016). Precio del dólar estadounidense en el mundo Procesos de Itô económicamente ponderados en un análisis espacial. Economía y Sociedad. 42 (20). 83-105. México.

YU, D. (2004). Modeling housing market dynamics in the city of Milwaukee: a geographically weighted regression approach. En internet: http://www.ucgis.org/ucgisfall2004/studentpapers/files/danlinyu.pdf

ZHOU, B.; Kockelman, K. M. (2008). Neighborhood impacts on land use change: A multinomial logit model of spatial relationships. Annals of Regional Science, 42(2), 321-340.

1. Departamento de Finanzas, Instituto Tecnológico Metropolitano – ITM. Correo electrónico: agudelotorres@hotmail.com

2. Departamento de Finanzas, Instituto Tecnológico Metropolitano – ITM

3. Departamento de Finanzas, Instituto Tecnológico Metropolitano – ITM