

Vol. 38 (Nº 22) Año 2017. Pág. 19
Jesús R. COHEN JIMÉNEZ 1; Nohora MERCADO-CARUSO 2; Harold PÉREZ OLIVEIRA 3; Tito Jose CRISSIEN- BORRERO 4; Jairo R. CORONADO-HERNÁNDEZ 5
Recibido: 17/11/16 • Aprobado: 15/12/2016
RESUMEN: En este trabajo se presentan modelos para crear planes CSP de muestreo por aceptación a través de modelos matemáticos estadísticos apoyado de las teorías de markov, cadenas de estados de markov y los diferentes planes de muestreo. De esta manera, se diseña un modelo matemático-estadístico bajo los lineamientos de las teorías bayesiana y markoviana de estados probabilísticos aplicados a los planes CSP de muestreo por aceptación en producción continua. Este modelo funciona como medio de control para la reducción de productos no conformes en la entrega a clientes con el propósito de mejorar la productividad y competitividad de la empresa. |
ABSTRACT: In this work presents models of statistical sampling plans for acceptance CSP supported Marcov theories, states of Markov chains and different sampling plans in this way to design a mathematical-statistical model under the guidance of the Bayesian theory and applied probabilistic Markov state CSP plans for acceptance sampling in continuous production function as control means for reducing non-conforming products delivery to customers by the company with production lines of this type, capable of improving competitiveness in international organizations and national and international markets, supported both in the technology resulting in reduced costs and increased productivity. |
En este artículo se presenta la conceptualización y las herramientas que permiten la realización de modelos matemáticos estadísticos para planes CSP de muestreos por aceptación. Los planes de muestreo de aceptación se han utilizado principalmente para la inspección de lotes salientes y entrantes. Estos planes, proporcionan reglas efectivas a los vendedores y compradores para tomar decisiones sobre la aceptación o el rechazo de un lote (Lee & Wu, 2016). Los planes de muestreo constituyen parte del control estadístico de procesos, el cual es considerado como un conjunto de herramientas para la gestión de la calidad para la mejora de procesos y productos (Ortíz & Felizzola, 2014). Por lo general, la característica de calidad se considera como límite inferior de especificación de un lote y se distribuye normalmente con una desviación estándar conocida y una media desconocida (Chung-Ho, 2016) .
Para el desarrollo de los modelos matemáticos presentados en este trabajo, se recopiló información concerniente con procesos markovianos, planes de muestreo de calidad saliente promedio (CSP) para producción en serie, por lotes y teoría bayesiana de probabilidad a través de artículos, textos, bases de datos. El procesamiento de la herramienta consiste en la aplicación sistematizada de los modelos estadístico-matemáticos para así, con base en la información proporcionada por el usuario, se pueda determinar el valor de los parámetros necesarios para el diseño del plan de inspección.
Para este artículo de investigación se analizó la problemática desde una perspectiva descriptiva, argumentativa, propositiva y cuantitativa con el apoyo de las teorías de markov y cadenas de estados markovianos, y los diferentes planes de muestreo, realizando un rediseño estadístico de las tablas CSP ya que los planes de muestreo CSP para la producción continua y por lotes están operacionalizados debido que al desarrollar el modelo, se simularon para observar y comparar los resultados obtenidos por el modelo matemático – estadístico; tomando los parámetros, variables y restricciones del caso.
Para una mejor comprensión de los modelos estadísticos para planes CSP, de muestreo por aceptación se define la Probabilidad condicional, como la Probabilidad de que se presente un evento, dado que otro evento ya se ha presentado (Malaver Rodríguez & Vargas Pérez, 2003). teniendo en cuenta que los Lote son el conjunto de recipientes primarios, o unidades de muestras, del mismo tamaño, tipo y forma de presentación, que contienen productos fabricados o elaborados en condiciones esencialmente análogas; en los planes CSP la Muestra son una o más unidades de producto extraídas de un lote o embarque, seleccionadas al azar sin importar su calidad. El número de unidades de producto en la muestra es el tamaño de muestra, diferente al Muestreo por variables la cual se utiliza para medir el monto de un universo. Para propósitos de auditoria, el objetivo del muestreo por variables es medir el monto verdadero del error de un saldo de cuentas. (Duncan, 2001)
Los aárboles de decisión, son particiones secuenciales del conjunto de datos realizadas para maximizar las diferencias de la variable dependiente o criterio base (Hair, Anderson, Tatham & Black, 1999, p. 718; Román & Lévy, 2003); conllevan, por lo tanto, la división de las observaciones en grupos que difieren respecto a una variable de interés (Armando, Aristizabal, & Velasquez Ceballos, 2010) señalan que mediante diferentes índices y procedimientos estadísticos se determina la partición que produce la mejor discriminación de acuerdo con unos criterios seleccionados. Teniendo en cuenta que los Proceso estocástico, en planes CSP estudian la interdependencia y el comportamiento límite de un conjunto de variables aleatorias del modelo y Proceso Markoviano son procesos estocásticos de decisión que se basan en el concepto de que la acción a formar en un estado determinado, en un instante determinado, depende solo del estado en que se encuentre el sistema al momento de tomar la decisión (Barbosa, 2005). En (Choy, yu, & Yeh, 2016) se estudia un plan de muestreo con variables secuenciales donde se hace la suposición que la calidad de un elemento de un lote se es una variable aleatoria con distribución exponencial. Para determinar el plan con el mínimo costo, se utiliza un enfoque markoviano combinado con redes bayesianas. En (Safe, Kazemzadeh, & Gholipour Kanani, 2016) se presenta una aplicación en el control de calidad por medio de cartas de control cartas que se obtienen a través del uso de las cadena de Markov.
En primera instancia, es importante entender que un proceso estocástico es un tipo de proceso aleatorio que evoluciona con el tiempo y se representa por un conjunto de funciones aleatorias x (t) donde t es el variable tiempo y a x (t) le corresponde una distribución de probabilidad (Barbosa, 2005).
F(x,t) = P { x (t) ≤ x } (1)
(Helfes & Lucantoni, 2006) demuestra que el número de llegadas en intervalos de tiempo adyacente, resultan de la superposición de múltiples fuentes homogéneas, tratadas mediante modelos de procesos de renovación. Naveas Ginno, Hernández Gastón (Millán Naveas & Lefranc Hernández, 2010)
Para el control estadístico de procesos, una de las etapas primordiales es la del muestreo por aceptación, el muestreo se realiza a los dos tipos de características de calidad manejadas estadística y matemáticamente: Variables y atributos. En (Franco Cardona, Velasquez Henao, & Olaya Morales, 2008) se encuentra que la serie presenta un patrón estacional deterministico de periodo anual y una tendencia estocástica; los modelos no lineales de regresión (Warren , 1994) pueden aproximar cualquier función continua definida en un dominio compacto (Cybenko, 1989 ; Ken-ichi , 1989; Hornik, 1989). Las revisiones realizadas por (Zhang y Patuwo 1997) demuestran que estos modelos han sido ampliamente usados en la predicción de series de tiempo. Los autores (VELÁSQUEZ, FRANCO & GARCÍA, 2009) señalan que una de las falencias importantes de este método es que no existe una metodología que se acepte de forma generalizada por la comunidad científica, si no una serie de pasos que son adaptados apartar de la hermenéutica según el conocimiento particular que se tenga de la serie. A en continuación se describe los planes CSP- 1, CSP- 2, CSP- 3, CSP de Nivel Múltiple que son los modelos a estudiar en la investigación.
Este plan empieza por una inspección del 100% del producto, de acuerdo con el orden de producción hasta que se logre encontrar cierta cantidad de unidades sucesivas sin defectos o no conformidades (Besterfield 1995). Al obtener esta cantidad, se interrumpe la inspección del 100% y se inicia la inspección por muestreo. La muestra es una fracción del flujo de producto y se escoge de manera que se reduzca al mínimo cualquier tendencia. Si se produce alguna no conformidad o defecto se interrumpe la inspección por fracción y se regresa a la inspección 100%. El número clave para la aprobación “i” es la cantidad de unidades conformes encontradas en una inspección de 100% y la frecuencia de muestreo es el cociente de unidades inspeccionadas se describe el funcionamiento del plan CSP–1 y el procedimiento a seguir para la implementación que es el mismo para el CSP – F, en la figura 1.

Figura1: Procedimiento para los planes csp – 1 y csp – f. Tomado de (Besterfield , 1995)
El plan de muestreo CSP – 2 es una modificación del plan CSP – 1 y su única diferencia es que una vez se inicia la inspección muestra de las unidades (una fracción “f” de ellas), la inspección 100% no se restablece al encontrar la primera unidad defectuosa, sino solamente en el caso que se presente una segunda unidad defectuosa en las siguientes “k” o menos unidades muéstrales inspeccionadas, donde k es el mismo numero de “i” unidades inspeccionadas, el procedimiento se muestra en la figura 2.
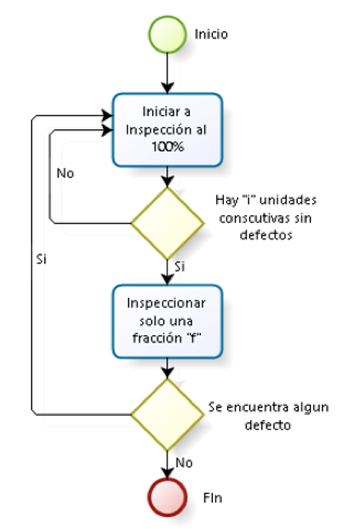
Figura2: procedimiento para los planes csp – 2. Tomado de (Besterfield , 1995)
Es un refinamiento del plan CSP – 2, y busca suministrar mayor protección contra un desmejoramiento de la calidad. Para esto cuando se encuentra la primera unidad defectuosa, deberán inspeccionarse las siguientes cuatro unidades de la línea de producción. Si ninguna de estas cuatro unidades consecutivas resulta defectuosa, el procedimiento de muestreo se continúa como el plan CSP-2. Si alguna de estas cuatro resulta defectuosa se restablece de inmediato la inspección 100% y se continúa bajo las reglas del CSP-2, como se muestra en la figura 3.
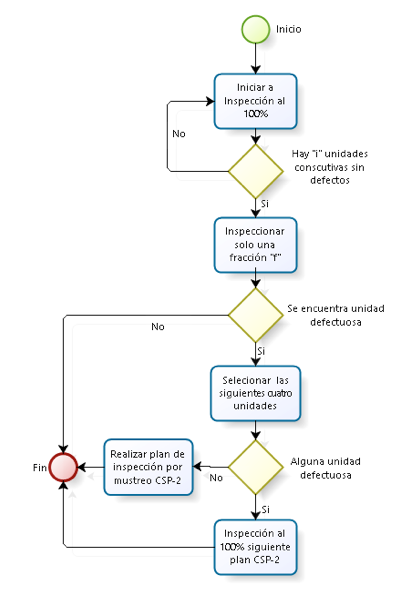
Figura 3: Procedimiento para los planes csp-3. Fuente: producción del autor
A continuación se describirán los modelos obtenidos, con base en la metodología antes expuesta, para los planes de inspección CSP-1 y CSP-2.
Modelo matemático-estadístico para los planes de inspección CSP-1
A continuación en la figura describe el funcionamiento del plan CSP-1. (Besterfield 1995) Y el procedimiento a seguir para la implementación, se muestra en la figura 1.
En el proceso del diseño del plan de muestreo CSP-1, intervienen varios parámetros, y el modelo se desarrolló para que al utilizarlo se pueda tener tres posibilidades de diseñar el plan de muestreo CSP-1, dependiendo de los parámetros que se deseen manipular.
Los parámetros que se utilizan en el diseño de CSP-1 son los siguientes:
Las tres posibilidades de diseñar el plan de muestreo CSP-1 dependiendo de los parámetros que se deseen manipular son las siguientes:
Se tiene como primera opción que se desee conocer el número de unidades conformes (i), tendiendo o fijando el límite de calidad promedio saliente, la fracción a inspeccionar y la fracción no conforme del proceso. Como lo muestra la figura 5.

Figura 5: Matriz de transición para CSP – 1. Fuente: producción del autor
E1: Inspección 100%.
E2: Inspección Fracción.
Donde:
P´: fracción no conforme del proceso, que es la proporción productos no conforme que entregue el proceso.
I: número de unidades conforme consecutiva.
De la matriz de transición se puede afirmar que las probabilidades Pij son las llamadas probabilidades de transición de la cadena de Markov X. es común disponer las Pij en una matriz cuadrada, llamada matriz de transición de la cadena de Markov X, el valor de P es no negativo, y la suma de las fila suman uno.
Y de esta matriz de transición resulta:

Donde:
X1*= Probabilidad de permanecer en estado inspección 100%.
X2*= Probabilidad de permanecer en estado de inspección fracción.

Es la probabilidad de permanecer en el estado E1 del plan, Inspección 100%.

Es la probabilidad de permanecer en el estado E2 del plan, Inspección fracción. Al tener las probabilidades de transición, se puede calcular el número de Unidades Inspeccionada y el número de unidades no conforme detectadas, para de este modo comprobar la eficiencia del plan CSP-1 como medio de control para la reducción de productos no conformes en la entrega a clientes por parte de la empresa con líneas de producción en serie y por lotes. Específicamente, se está hablando de hallar el número de unidades conformes (i), tendiendo o fijando el límite de calidad promedio saliente, la fracción a inspeccionar y la fracción no conforme del proceso. De la matriz de transición y sus probabilidades con los parámetros que se desean fijar, que se encuentran involucrados en el diseño del plan CSP-1, al realizar los despejes respectivos resultan las siguientes fórmulas que fueron utilizadas para el diseño de la herramienta.
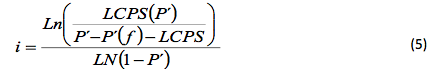
La segunda opción es que se desee conocer cual será la fracción a inspeccionar (f), teniendo o fijando el limite de calidad promedio saliente “LCPS”, el número de unidades a inspeccionar (i) y la fracción no conforme del proceso P´.

La tercera opción es que se desee conocer cual es su limite calidad promedio saliente “LCPS”, teniendo estipulados el numero de unidades conformes (i), la fracción a inspeccionar (f), y la fracción no conforme del proceso P´.

El funcionamiento del plan CSP-2 a diferencia del proceso del diseño del plan CSP-1, en el proceso del diseño del plan de muestreo CSP-2, interviene un nuevo parámetro, ya que se tiene una parte del proceso en la que la inspección al 100% no volverá a implantarse, cuando la producción esté bajo inspección del muestreo, hasta que se hayan encontrado dos unidades defectuosas dentro del espacio de k unidades de muestras entre ellas. Los parámetros que se utilizara en el diseño de CSP-2 son los siguientes:
Ha encontrado una no conforme, no se regrese al sistema 100% (k). Las cuatro posibilidades de diseñar el plan de muestreo CSP-2 dependiendo de los parámetros que se deseen manipular son las siguientes:
La primera opción es que se desee conocer cuál seria el numero de unidades consecutivas conformes (i), tendiendo o fijando el limite de calidad promedio saliente, la fracción a inspeccionar (f), la fracción no conforme del proceso, y el número de unidades consecutivas conformes (k) requeridas para que, dado que se ha encontrado una no conforme, no se regrese al sistema 100%.
Para lo anterior lo primero que tuvo en cuenta fue identificar los estados, ya que se debía diseñar la matriz de transición que se tendría como base para el diseño del modelo matemático a utilizar.
E1: Inspección 100%.
E2: Inspección Fracción. Donde esta incluido la inspección de las K unidades consecutivas conformes inspeccionadas requeridas para que, dado que se ha encontrado una no conforme, no se regrese al sistema 100%, como lo muestra la figura 6.

Figura 6: Matriz de transición de transición para CSP-2. Fuente: Producción del autor
Donde:
P´: fracción no conforme del proceso que es la proporción productos no conforme que entregue el proceso.
i: número de unidades conforme consecutiva.
k: Número de unidades consecutivas conformes requeridas para que, dado que se ha encontrado una no conforme, no se regrese al sistema 100% (k).
De la matriz de transición se puede afirmar que las probabilidades Pij son las llamadas probabilidades de transición de la cadena de Markov X. es común disponer las Pij en una matriz cuadrada P llamada matriz de transición de la cadena de Markov X, toda entrada de una matriz de transición P es no negativo, y los términos de cualquier fila suman uno.
Y de esta matriz de transición resulta:

Es la probabilidad de permanecer en el estado E2 del plan, Inspección Fracción.
Al tener las probabilidades de transición, se puede calcular el número de Unidades Inspeccionada y el número de unidades no conforme detectadas. Para de este modo comprobar la eficiencia del plan CSP-2 como medio de control para la reducción de productos no conformes en la entrega a clientes por parte de la empresa con líneas de producción en serie y por lotes.
Para hallar el número de unidades consecutivas conformes (i), tendiendo o fijando el limite de calidad promedio saliente “LCPS”, la fracción a inspeccionar (f), la fracción no conforme del proceso P´, y el número de unidades consecutivas conformes (k) requeridas para que, dado que se ha encontrado una no conforme, no se regrese al sistema 100%, al realizar los despejes respectivos resultan las siguientes formulas que fueron utilizadas para el diseño de la herramienta.

La segunda opción es que se desee conocer cual será la fracción a inspeccionar (f), teniendo o fijando el limite de calidad promedio saliente “LCPS”, el numero de unidades consecutivas conformes (i), la fracción no conforme del proceso P´ y el número de unidades consecutivas conformes (k) requeridas para que, dado que se ha encontrado una no conforme, no se regrese al sistema 100%.
La tercera opción es que se desee conocer cual es número de unidades consecutivas conformes requeridas para que, dado que se ha encontrado una no conforme, no se regrese al sistema 100% (k). Teniendo estipulados el número de unidades consecutivas conformes (i), la fracción a inspeccionar (f), la fracción no conforme del proceso P´ y el límite de calidad promedio saliente LCPS.
La cuarta opción es que se desee conocer cual es su limite calidad promedio saliente “LCPS”, teniendo estipulados el numero de unidades consecutivas conformes (i), la fracción a inspeccionar (f), la fracción no conforme del proceso P´ y el número de unidades consecutivas conformes (k) requeridas para que, dado que se ha encontrado una no conforme, no se regrese al sistema 100%.
En el proceso del diseño del plan de muestreo CSP-3, el modelo se desarrolló para que, al utilizarlo, se pudiera contar con cuatro posibilidades para el diseño del plan de muestreo CSP-3, dependiendo de los parámetros que se deseen manipular. Los parámetros que se utilizan en el diseño de CSP-3 son los siguientes:
Las posibilidades de diseñar el plan de muestreo CSP-3 dependiendo de los parámetros que se deseen manipular son las siguientes:
La primera opción es cuando se desee conocer cuál sería el número de unidades consecutivas conformes (i), tendiendo o fijando el límite de calidad promedio saliente, la fracción a inspeccionar, la fracción no conforme del proceso, y el número de unidades consecutivas conformes (k) requeridas para que, dado que se ha encontrado una no conforme, no se regrese al sistema 100%.
Para lo anterior lo primero que se debe tener en cuenta es identificar los estados, ya que se debe de diseñar la matriz de transición que sirve como base para el diseño del modelo matemático a ser utilizado para el funcionamiento de la herramienta. Se identifican de los conceptos dos estados.
E1: Inspección 100%.
E2: Inspección Fracción.
E3: Inspección de las k unidades consecutivas conformes inspeccionadas requeridas para que, dado que se ha encontrado una no conforme, no se regrese al sistema 100%.
E4: Inspección de las 4 unidades siguientes de la línea de producción.
Realizando la matriz de transición para CSP – 3 en donde:
P´: fracción no conforme del proceso que es la proporción productos no conforme que entregue el proceso.
i: Número de unidades conforme consecutiva.
k: Número de unidades consecutivas conformes requeridas para que, dado que se ha encontrado una no conforme, no se regrese al sistema 100% (k).
De la matriz de transición se puede afirmar que las probabilidades Pij son las llamadas probabilidades de transición de la cadena de Markov X. es común disponer las Pij en una matriz cuadrada llamada matriz de transición de la cadena de Markov X, el valor de P es no negativo, y la suma de las fila suma uno.
Al tener las probabilidades de transición, se puede calcular el número esperado de unidades inspeccionada y el número esperado de unidades no conforme detectadas, para de este modo comprobar la eficiencia del plan CSP-3 como medio de control para la reducción de productos no conformes en la entrega a clientes por parte de la empresa con líneas de producción en serie y por lotes.
La segunda opción es que se desee conocer cuál sería la fracción a inspeccionar (f), teniendo o fijando el límite de calidad promedio saliente “LCPS”, el numero de unidades consecutivas conformes (i), la fracción no conforme del proceso P´ y el número de unidades consecutivas conformes (k) requeridas para que, dado que se ha encontrado una no conforme, no se regrese al sistema 100%.
La tercera opción es que se desee conocer cuál es número de unidades consecutivas conformes requeridas para que, dado que se ha encontrado una no conforme, no se regrese al sistema 100% (k), teniendo estipulados el número de unidades consecutivas conformes (i), la fracción a inspeccionar (f), la fracción no conforme del proceso P´ y el límite de calidad promedio saliente LCPS.
La cuarta opción es que se desee conocer cuál es el límite de calidad promedio saliente “LCPS”, teniendo estipulados el número de unidades consecutivas conformes (i), la fracción a inspeccionar (f), la fracción no conforme del proceso P´ y el número de unidades consecutivas conformes (k) requeridas para que, dado que se ha encontrado una no conforme, no se regrese al sistema 100%.

A través del análisis realizado de los modelos matemáticos, se pudo apreciar hasta qué punto se podría perder dinero por tomar decisiones erróneas al considerar ciento por ciento correctas las predicciones de los inspectores, máquinas inspectoras o métodos de inspección. En este sentido, los errores en las decisiones del inspector conllevan a la retención injusta de unidades conformes y cuyo costo asociado está representado por el costo de fabricación de dichas unidades que debieron haber sido despachadas pero fueron retenidas por error tipo I del inspector. Por otro lado, se tiene el caso de las unidades no conformes despachadas, las cuales implican gastos innecesarios de envío y podrían ocasionar penalidades por parte de los clientes. Cuando un cliente elige un proveedor siempre se tiene en cuenta las referencias sobre la organización y su comportamiento dentro del mercado, en el momento de que el cliente escoja a su proveedor. Por otro lado también se debe tener en cuenta aquellas certificaciones de calidad que las empresas obtienen para demostrar al cliente, que por medio de entes especializados que demuestran de una forma legal la calidad de una empresa, con la ayuda de los planes de muestreo CSP. Para hacer posible la implementación de estos planes dentro de una empresa, se hace necesario que cada miembro de esta se involucre, sabiendo que el buen funcionamiento de los planes de muestreo harán posible los propósitos planteados anteriormente. Se puede concluir que aplicar los planes CSP dentro de las empresas permiten dar más seguridad en cuanto a la mejora de calidad de los despachos, y de esta forma el cliente estará más satisfecho y nuestra imagen ante el mercado será mejor calificada.
Helfes, H., & Lucantoni. (2006). A Markov Modulated Characterization of Packetized Voice and Data Traffic and Related Statistical Multiplexer Performance. IEEE Journal on Selected Areas in Communications (4), 856 - 868.
Millán Naveas, G., & Lefranc Hernández, G. (2010). INCLUSIÓN DE CORRELACIONES TEMPORALES CON DEPENDENCIA A LARGO PLAZO Y PATRONES AUTOSIMILARES EN MODELOS DE REDES IEEE 802.3. Ingeniare. Revista chilena de ingeniería , 18, 95-104.
Franco Cardona, C. J., Velasquez Henao, J. D., & Olaya Morales, Y. (2008). Caracterizacion de la demanda mensual de electricidad en Colombia usando un modelo de componentes no observables. Cuaderno de administraciòn , 221-235.
Warren , S. (1994). Neural networks and statistical models. SAS Institute Inc., Cary, NC, USA , 1538-1550.
Cybenko, M. (1989). Approximation by superpositions of a sigmoidal function. 2, 303–314.
Ken-ichi , F. (1989). the approximate realization of continuous mappings by neural networks. Neural Neworks. Neural Networks , 183–192.
Hornik, K. (1989). Multilayer feedforward networks are universal approximators. Neural Network , 359-366.
Barbosa. (2005). Notas de Clase “CSP con MARKOV".
ARMANDO LENIN , T. A., ARISTIZÁBAL VELÁSQUEZ, R. E., & HERMILSON , V. C. (07 de 2010). Estimación de las provisiones esperadas en una institución financiera utilizando modelo logit y probit. Revista ciencias estratégicas , 259-270.
Duncan, A. (2001). CONTROL DE CALIDAD Y ESTADISTICA INDUSTRIAL. 1088.
DAVID VELÁSQUEZ, J., FRANCO, C. J., & ALONSO GARCÍA, H. (2009). UN MODELO NO LINEAL PARA LA PREDICCIÓN DE LA DEMANDA MENSUAL DE ELECTRICIDAD EN COLOMBIA. 25.
Besterfield , D. (1995). Control de Calidad. PRENTICE HALL HISPANOAMERICANA S.A.
Araya. (1994). Induction of decision Tree when Examples are Described with Noisy Measurements and with Fuzzy Class Membership.
Zhang, G., & Patuwo, E. (1997). Forecasting with artificial neural networks: The state of the art. International Journal of Forecasting , 35-60.
H. I. Lee, A., & Wei Wu, C. (2016). A modified variables repetitive group sampling plan with the consideration of preceding lots information. Annals of Operations Research , 355–373.
Ortíz Barrios, M. A., & Felizzola Jiménez, H. A. (2014). Metodología miceps para control estadístico de procesos: caso aplicado al proceso de producción de vidrio templado. Prospect , 12 (2), 73-81.
Chung-Ho, C. (2016). Optimum process mean setting with specified average outgoing quality limit protection for variable single sampling plan. Journal of Statistics and Management Systems , 19, 499-508.
Choy, B., yu, P., & Yeh, l. (2016). A sequential sampling plan for exponential distribution. Sequential Analysis,. Sequential Analysis , 35, 331-336.
Safe, H., Kazemzadeh, R., & Gholipour Kanani, y. (Octubre de 2016). A Markov Chain Approach for Double-Objective Economic statistical Design of the Variable Sampling Interval X‾ Control Chart. Communications in Statistics - Theory and Methods .
1. Doctor (e) en Ingeniería Industrial, Magister en Ingeniería Industrial, Ingeniero Industrial, Docente Asociado Universidad. Barranquilla, Colombia ,jesuscohenjimenez@gmail.com
2. Máster en Ingeniería de Sistemas. Profesor Adjunto. Universidad de la Costa. Barranquilla, Colombia. nmercado1@cuc.edu.co
3. Magister en Ingeniería Industrial, Ingeniero Industrial, Decano Facultad de Ingenierías Corporación Universitaria Americana, Barranquilla, Colombia, hperez@coruniamericana.edu.co
4. Magister en Educación. Magister en Administración. Administrador de Empresas. Rector de la Universidad de la Costa (CUC). Docente – Investigador de la Facultad de Educación y Ciencias Económicas de la Universidad de la Costa (CUC) (Barranquilla, Colombia). E – mail: rectoría@cuc.edu.co
5. Doctor Ingeniero Industrial. Profesor Titular del Departamento de Ingeniería Industrial. Líder grupo de investigación PRODUCOM. Universidad de la Costa. Barranquilla, Colombia. jcoronad18@cuc.edu.co