

Vol. 38 (Nº 21) Año 2017. Pág. 26
Thiago Floriani STEPKA 1; Gilvan Alberto ZENY JUNIOR 2; Gerson dos Santos LISBOA 3; Clebson Lima CERQUEIRA 4; Vagner Alex PESCK 5; Mailson ROIK 6
Recibido: 12/11/16 • Aprobado: 26/12/2016
RESUMO: Realizou-se a modelagem volumétrica de árvores com diâmetro médio quadrático (dg) e dominantes (ddom) de um povoamento multiâneo de Pinus taeda L. localizado na região dos Campos Gerais no estado do Paraná, Brasil. Realizou-se a modelagem volumétrica com uso de três modelos matemáticos tradicionais (Schumacher, Spurr e Berkhout) e o ajuste de três funções de afilamento (Kozak, Prodan e Hadetzky). Observou-se um fator de forma artificial médio foi de 0,4555, enquanto que para as árvores médias quadráticas (dg) e dominantes (ddom), foram, respectivamente, 0,4617 e 0,4493. O modelo de afilamento e volumétrico que melhor se ajustaram aos dados foram, respectivamente o Polinômio de Potências Fracionárias de Hadetzky e o modelo de Schumacher. |
ABSTRACT: Was performed volumetric modeling trees with quadratic average diameter (dg) and dominant (ddom) a all-aged forest of Pinus taeda L. located in the Campos Gerais region in the state of Paraná, Brazil. It was performed volumetric modeling with use of three traditional mathematical models (Schumacher, Spurr and Berkhout) and adjusting three functions tapering (Kozak, Prodan and Hadetzky). There was an average artificial form factor was 0.4555, while for average quadratic trees (dg) and dominant (ddom) were, respectively, 0.4617 and 0.4493. The taper and volumetric model that best fit the data were respectively the polynomial of fractional of Hadetzky and model of Schumacher. |
As técnicas de mensuração florestal são importantes ferramentas utilizadas no manejo de povoamentos florestais, permitindo obter informações de variáveis dendrométricas, auxiliando no planejamento e na tomada de decisões.
Nos inventários florestais uma das principais funções do ponto de vista econômico é estimar o estoque de madeira do povoamento e sua produção a fim de direcionar a matéria-prima para diferentes usos. Existem várias formas de estimar o volume de uma árvore, dentre elas, pelo uso de um fator de forma (natural ou artificial), quociente de forma, equações de volume e/ou funções de afilamento.
O estudo detalhado de uma população exige a observação e análise de uma série de variáveis, sendo que algumas delas são fáceis de mensurar e outras de difícil obtenção como o diâmetro ao longo do tronco. Entretanto se forem correlatas, pode-se determinar, indiretamente, as variáveis difíceis a partir das variáveis de fácil obtenção (FINGER, 1992).
Conhecer o afilamento do tronco das árvores é importante para o planejamento e execução de atividades florestais, principalmente quando se deseja classificar a produção pelas toras de madeira, segundo as metas estabelecidas para o talhão. Ao associá-lo à função de crescimento, a descrição matemática do afilamento permite inferir na quantidade e dimensão das toras de forma dinâmica, simulando cenários de custo e renda os quais podem auxiliar na definição da rotação da floresta (COSTA et al., 2016).
Para proporcionar o uso múltiplo do tronco de uma árvore, faz-se necessário o conhecimento do afilamento do tronco, do volume e dimensão dos seus sortimentos, possibilitando, assim, o planejamento e o estudo da viabilidade econômica de um empreendimento florestal (PEREIRA et al., 2005).
Os estudos da exatidão das estimativas obtidas apontam que a modelagem com uso de funções de afilamento são ferramentas essenciais para maximizar a obtenção de produtos florestais de alto valor agregado em florestas produtivas. No Brasil, especialmente em povoamentos de Pinus spp., onde o destino final do produto são processos como serraria e laminação, essa ferramenta assume grande importância. Dessa forma, os estudos para o desenvolvimento de funções de afilamento são muito relevantes, pois permitem definir os diferentes produtos possíveis de serem obtidos a partir de um mesmo tronco para o processamento industrial, aumentando consequentemente seu aproveitamento (PIMENTEL, 2009).
A forma do tronco da árvore é a sua configuração externa, que a rigor não se identifica com a forma de um único sólido geométrico, mas sim com vários, segundo a porção do tronco considerada (HUSCH et al., 1982).
A forma das árvores possui uma variação muito grande dentro da floresta. Esta variação ocorre devido à diminuição do diâmetro em direção ao topo da arvore, que e conhecida como “taper” ou afilamento, afetando diretamente o volume e variando com a espécie, idade, espaçamento entre árvores e condições do sítio (MÜLLER, 2004).
Dentre as diversas técnicas estatísticas de modelagem empregadas para descrição do perfil de troncos, destacam-se os modelos polinomiais não-segmentados (EISFELD et al., 2004), que conseguem aliar eficiência a certa simplicidade de aplicação, quando comparados com os polinômios segmentados.
A estimativa do volume de madeira em povoamentos florestais é uma das principais preocupações para os gestores florestais como uma maneira de determinar o rendimento econômico. A estimativa do volume de árvore individual é preferida porque resulta em erros muito menores do que a estimativa por unidade de área (Teshome, 2005). Contudo, a estimativa do volume comercial determina as dimensões da madeira colhida e têm grande influência no rendimento econômico.
Para Müller (2004) a equação de forma de tronco permite conhecer o diâmetro a uma determinada altura ou comprimento de tora, bem como o comprimento em que se encontra um determinado diâmetro, permitindo direcionar a tora segundo sua mais rentável utilização. Segundo o mesmo autor, a utilização de equações de forma de tronco possibilita descrever o perfil do tronco e, por integração, obter a estimativa do volume total e parcial em diferentes seccionamentos com grande precisão, permitindo também a confecção das tabelas de sortimentos. Sendo a função de forma uma descrição matemática do perfil longitudinal de um tronco, e desenvolvida com o propósito de permitir estimativas de forma e volume de uma árvore, baseando-se somente no seu diâmetro a altura do peito e na altura total (MÜLLER, 2004).
Os modelos de afilamento são relações funcionais que permitem descrever o perfil longitudinal do tronco. São funções consideradas dinâmicas, porque possibilitam a estimativa do diâmetro (di) de dada altura (hi) e altura a qualquer diâmetro especificado, como também servem para fazer o sortimento e estudar a evolução da forma da árvore ao longo de sua vida (KOZAK et al., 1969).
Dada à importância dos estudos de modelagem, objetivou-se neste trabalho avaliar o desempenho de modelos de afilamento e volumétricos para a estimativa do volume individual de Pinus taeda L. para árvores médias quadráticas e dominantes na região dos Campos Gerais, no Estado do Paraná, Brasil.
A área de estudo está localizada na Fazenda do Lago, distrito de Guaragi no município de Ponta Grossa, PR entre as coordenadas geográficas 25º16’58” S e 50º10’34” W, pertencente a Montenegro Indústria, Comércio e Transporte de Madeira S.A. Trata-se de um plantio de 92,8 ha de Pinus taeda L. com 3 idades sendo elas: 9 anos (19,9 ha), 8 anos (35,2 ha) e 6 anos (37,7 ha) conforme pode ser observado na Figura 1. As idades são referentes à época da realização do inventário florestal ocorrida no ano de 2015.

Figura 1. Área de estudo, talhões, e suas respectivas idades.
Os plantios foram realizados com espaçamento de 2,5 X 2,5 m (1600 árvores/ha), não havendo intervenções no povoamento até a data da coleta das informações biométricas, ocorrendo apenas poda com retirada de 50% da copa verde quando as árvores possuíam três anos de idade.
No ano de 2015 realizou-se um inventário florestal com uso 33 unidades amostrais circulares de 400 m² cada, distribuídas sistematicamente, nas quais foram avaliadas as variáveis dendrométricas (diâmetro e alturas) e a localização das árvores com diâmetro médio quadrático (dg) e as árvores dominantes (ddom), seguindo a proposta de Assman (1970).
Em cada unidade amostral, foram abatidas duas árvores, sendo uma a árvore com diâmetro médio quadrático (dg) e a outra dominante (ddom). Para a obtenção do volume real, foram cubadas 66 árvores pelo método de Smalian. Sobre as seções foram medidos os diâmetros (di) com casca a 0,1 e 1,3 m e a partir deste ponto a cada 2,0 m até a altura total da árvore.
Após a cubagem rigorosa das 66 árvores (33 dg e 33 ddom), foram ajustados três modelos volumétricos e três modelos de afilamento (Tabela 1), além de serem obtidos os fatores de forma artificial para cada árvore cubada. O ajuste foi realizado, separadamente, para as árvores dg e árvores ddom e, ainda para todo o conjunto de dados, com o objetivo de verificar se existem diferenças entre as equações para representar as árvores médias e dominantes.
Ressalta-se que os “modelos três e quatro”, função de afilamento de Hadetzky, encontram-se apresentados após a seleção das variáveis independentes por meio do procedimento de Stepwise. Todos os demais ajustes foram desenvolvidos por meio de análise de regressão linear.
O procedimento Stepwise é, provavelmente, a técnica mais utilizada de seleção de variáveis. O procedimento constrói interativamente uma sequência de modelos de regressão pela adição ou remoção de variáveis em cada etapa. O critério para adicionar ou remover uma variável em qualquer etapa é geralmente em função de um teste parcial F. A regressão Stepwise começa formando um modelo com uma variável, usando a variável preditora que tenha a mais alta correlação com a variável de resposta.
Tabela 1. Modelos utilizados para expressar a forma e o volume das árvores.

Devido à flexibilidade das funções de afilamento para estimar volume, diâmetro e altura, dentre outros, foi selecionado o modelo de Kozak. Ressalta-se que este é o modelo mais difundido entre os profissionais da área florestal, devido a facilidade no ajuste e precisão das estimativas (KOZAK, et al., 1969).
No modelo de Kozak a variável dependente é expressa pelo quadrado da razão entre o diâmetro em determinada altura e o dap. As variáveis independentes são a razão entre a altura em determinado diâmetro e a altura total. O modelo é representado por:

Admitindo-se que a seção transversal em qualquer parte do tronco é circular, o volume pode ser obtido por integração matemática da área seccional ao longo do eixo do tronco. Considerando o volume (m³), o diâmetro (dap) em cm, podemos escrever a integral da seguinte forma:
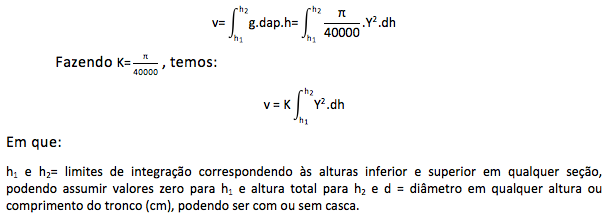
O volume da primeira tora foi obtido através da integração do modelo ajustado. A integração do modelo permite que se façam estimativas dos volumes na ponta fina das toras, ou seja, volume de toras com um comprimento e diâmetro pré-estabelecido para determinado fim. Portanto, permite estabelecer os multiprodutos da floresta como o volume para laminação, serraria, celulose e energia. Neste caso, mede-se di para classificar a tora dentro das classes de diâmetro, já que o volume é em função do dap, ht e hi. A equação ajustada e transformada algebricamente para a estimativa do volume é:
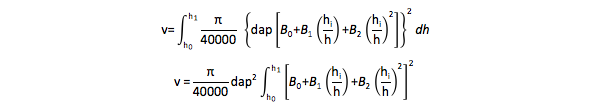
A integral da função está apresentada abaixo na qual pode ser utilizada para a estimativa do volume total ou para diferentes porções do tronco:

O procedimento para o polinômio do quinto grau (Prodan) segue o mesmo desenvolvimento. A curva de ajustamento dos diâmetros relativos em função das alturas relativas e representada pela função polinomial do quinto grau, expressa por:
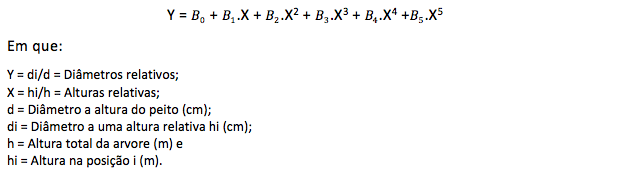
Substituindo as variáveis dependente e independente na equação original, obtém-se, desta forma, a nova equação, sendo expressa por:

A equação ajustada e transformada algebricamente para a estimativa do volume é:

O modelo de Hadetsky segue o mesmo desenvolvimento do modelo polinomial do 5º grau. A curva de ajustamento dos diâmetros relativos em função das alturas relativas e representada pela função polinomial, expressa por:

A equação ajustada e transformada algebricamente para a estimativa do volume das árvores dominantes e para a totalidade das árvores é:

A seleção da melhor equação baseou-se nas estatísticas de ajuste de precisão, como coeficiente de determinação ajustado (R² aj.), erro padrão da estimativa em porcentagem (Syx%) e pela análise dos resíduos.
Para todo o conjunto de dados, foi possível observar um fator de forma artificial médio de 0,4555. Analisando-se separadamente as árvores médias quadráticas (dg) e dominantes (ddom), verificou-se, respectivamente, fatores de forma artificial médio de 0,4617 e 0,4493, indicando que as árvores médias quadráticas tendem a ser mais cilíndricas que as árvores dominantes, possivelmente pelo fato das árvores dg serem mais afetadas no interior da florestal o que denota-se que o aumento do densidade da floresta pode aumentar o fator de forma dos indivíduos.
As estimativas dos coeficientes da regressão e as estatísticas de precisão obtidos nos ajustes dos modelos de afilamento para estimativa do volume total das árvores de Pinus taeda L. para os ajustes considerando as árvores médias quadráticas, dominantes e para todo o conjunto de dados, são apresentados na Tabela 2.
Observa-se que no ajuste dos modelos de afilamento para todo o conjunto de dados, os valores de coeficientes de determinação ajustados (R²aj.) variaram entre 0,90 e 0,98 e erro padrão da estimativa relativo (Syx%) entre 12,2% e 14,0%. Os ajustes realizados para as árvores médias quadráticas apresentaram coeficiente de determinação ajustado (R²aj.) variando entre 0,83 e 0,85, e erro padrão da estimativa relativo (Syx%) entre 13,1% a 14,3%. Para as árvores dominantes os ajustes apresentaram valores de coeficiente de determinação (R²aj.) de 0,87 a 0,89 com erro padrão da estimativa em torno de 11,4% a 13,1%. Esses resultados são semelhantes aos encontrados por Yoshitani Junior et al. (2011), e inferiores aos encontrados por Téo et al. (2013). Em estudos da forma do tronco para estimativa do volume de árvores do gênero Pinus na Região Sul do Brasil.
Tabela 2: Estatísticas e coeficientes dos modelos de afilamento ajustados.
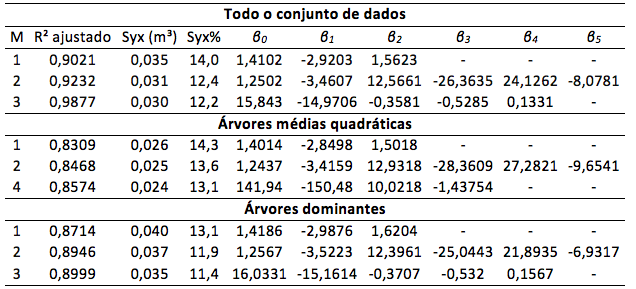
Dentre os três modelos de afilamento ajustados, o de Hadetzky (3) foi o que obteve melhor acurácia, em todas as situações de ajuste para a estimativa do volume, apresentando o menor valor de Syx (12,2%) e maior valor de R2aj. (0,98) para o banco de dados total. Para as árvores médias quadráticas foi encontrado o menor valor de Syx (13,1%) e maior valor de R2aj. (0,85), assim como para as árvores dominantes com o menor valor de Syx (11,4%) e maior valor de R2aj. (0,89).
No Brasil, a maioria dos trabalhos para o gênero Pinus tem sido realizado para as espécies Pinus elliottii e principalmente para Pinus taeda. Diversos autores têm desenvolvido trabalhos com o intuito de modelar a forma e estimar o diâmetro e volume ao longo do tronco dessas espécies. Destacam-se os trabalhos conduzidos por NOGUEIRA et al. (2008); YOSHITANI JUNIOR et al. (2011); KOHLER et al. (2013); TÉO et al. (2013); MÔRA (2015); SCHRODER et al. (2015); KOHLER et al. (2016) e SOUZA et al. (2016).
Yoshitani Junior et al.(2011) testando modelos de afilamento para Pinus taeda, entre eles o de Hradtezky, constatou que o modelo de Hradtezky foi o melhor para estimativa do volume, com valor de Syx (12,8%) e R²aj. (98,2%). Esse resultado é inferior ao encontrado no presente estudo para estimativa do volume de árvores do conjunto de dados total e dominantes, sendo superior apenas no ajuste realizado para as árvores médias quadráticas.
Téo et al.(2013) testando três modelos de afilamento, entre eles o de Hradetzky com melhor ajuste para Pinus elliottii em diferentes idades, encontraram valores de Syx (10,68%) e R²aj. (0,92). Resultado superior ao encontrado no presente estudo para Pinus taeda. Estes autores constataram que as funções de afilamento de melhor desempenho para estimativa do volume total foram o Polinômio de 2º Grau para 10 e 27 anos e o Polinômio de Potências Fracionárias de Hradetzky para 18 anos de idade. Kohler et al. (2016) ajustaram este mesmo modelo para evolução do afilamento do tronco em povoamentos de Pinus taeda e encontraram valores de Syx% (5,4 a 7,6) e R²aj. (0,98 a 0,99) satisfatórios em todas as classes de idades, concluindo que o modelo de Hradetzky representa adequadamente a evolução da forma do tronco das árvores.
Yoshitani Junior et al.(2011); Kohler et al. (2013); Teo et al.(2013) e Kohler et al. (2016), avaliaram diversas funções de afilamento para estimativa do diâmetro e volume de Pinus taeda, no estado do Paraná. Os referidos autores recomendaram o Polinômio de Potências Fracionárias (Hradetzky) para estimativa dos diâmetros e volume ao longo do tronco das árvores de Pinus taeda. Contudo, estes trabalhos corroboram o presente estudo, em que o modelo de Hadetzky também obteve melhor acurácia de ajuste para estimativa do volume total das árvores de Pinus taeda (Tabela 2).
Para a avaliação do desempenho de modelos estatísticos, faz-se necessário análises mais minuciosas e cuidadosas, que garantam a acurácia dos ajustes. Assim a análise gráfica de resíduos é fundamental, visto que erros grosseiros podem ocorrer em determinados cenários e não ser detectados pelas estatísticas de precisão, tais como o coeficiente de determinação (R²aj.), erro padrão da estimativa (Syx). Neste sentido, Draper; Smith (1966) destacam que nenhuma equação de estimativa deve ser usada antes de se proceder a análise gráfica de resíduos, mesmo os índices de ajuste (R² aj.) e de precisão (Syx) sendo considerados satisfatórios. Para o presente estudo foi realizado a análise gráfica de resíduos (%) dos modelos de volume e de afilamento, para verificação de eventuais tendenciosidades (Figura 2 e 3).

Figura 2: Dispersão dos resíduos dos modelos de afilamento para todo o conjunto de dados (Total),
árvores média quadráticas (dg) e árvores dominante (ddom).
Na Tabela 3, são apresentados os coeficientes da regressão e as estatísticas de precisão dos três modelos volumétricos ajustados para estimativa do volume total com casca para Pinus taeda L No ajuste realizado para todo o conjunto de dados, os valores de coeficiente de determinação ajustado (R2aj.) variaram de 0,84 a 0,94 com erro padrão da estimativa relativo variando entre 10,4% a 17,5%. O ajuste realizado para as árvores médias quadráticas apresentou valores de coeficiente de determinação ajustado (R2aj.) variando de 0,78 a 0,88 com erro padrão da estimativa relativo entre 11,7% a 16,1%. Para as árvores dominantes observou-se valores de coeficiente de determinação ajustado (R2aj.) entre de 0,80 e 0,94 e erro padrão da estimativa relativo variando de 8,6% a 16,2%.
Os modelos de dupla entrada (1 e 2), apresentaram estatísticas de ajuste superiores se comparado com o modelo (3) de simples entrada. Esses resultados corroboram os valores encontrados em trabalhos realizados por diversos autores, destacando-se os trabalhos de Thomas et al. (2006); Pelissari et al. (2011) e Silvestre et al. (2014).
Tabela 3: Estatísticas e coeficientes dos modelos volumétricos ajustados.

M.= Modelo; 1= Schumacher; 2= Spurr; 3= Berkout
Dentre as três equações de volume ajustadas, a de Schumacher obteve melhor acurácia com os valores das estatísticas de avaliação superiores em todas as situações de ajuste para estimativa do volume total com casca, apresentando o menor valor de Syx (10,4%) e maior valor de R2aj. (0,94) para conjunto de dados total. Para as árvores médias quadráticas foi encontrado menor valor de Syx (11,7%) e maior valor de R2aj. (0,88). As árvores dominantes apresentaram o menor valor de Syx (8,6) e maior valor de R2aj. (0,94). Campos e Leite (2013) afirmaram que esse modelo é um dos mais difundidos no meio florestal para expressar o volume de madeira em função do diâmetro e da altura total ou comercial, uma vez que resulta em estimativas geradas por esta equação quase sempre não tendenciosas.
Os resultados encontrados para o modelo volumétrico com melhor desempenho estatístico no presente trabalho estão coerentes em relação aos encontrados em outros trabalhos, com valores de coeficiente de determinação quase sempre se situando-se entorno de 0,9 e erro padrão da estimativa, que na maioria dos casos apresentam-se inferiores a 10% nos melhores ajustes (THOMAS et al. 2006; AZEVEDO et al., 2011; PELISSARI et al. 2011; SILVESTRE et al. 2014; LEAL et al., 2015). Isso demostra que a variação dos dados foi satisfatoriamente explicada pelo ajuste do modelo.
A análise gráfica dos resíduos (Figura 3) permitiu verificar a ausência de tendenciosidades no ajuste dos modelos volumétricos e de afilamento, demonstrando que a avaliação das estatísticas complementares proporciona a seleção de ajustes adequados para a estimativa da variável volume em função do diâmetro e altura pelas equações de volume e funções de afilamento.

Figura 3: Dispersão dos resíduos dos modelos volumétricos para todo o conjunto de dados (Total), árvores média quadráticas (dg) e árvores dominantes.
Os gráficos de resíduos em função do DAP para as três situações de ajuste do modelo de Schumacher, estão aproximadamente distribuídos em torno de zero, com variância constante ao longo da linha de regressão. Foi observado que os resíduos apresentam maior homogeneidade de variância quando o ajuste do modelo foi realizado para as árvores dominantes. Nota-se também nos gráficos de distribuição dos resíduos para as funções de afilamento uma distribuição em torno de zero, com variância constante ao longo da linha de regressão. No entanto, foi observado maior homogeneidade de variâncias para o modelo de Hadetzky, e principalmente no ajuste realizado para as árvores dominantes.
Considerando os critérios de avaliação dos modelos pelos valores das estatísticas Syx e R2aj. e análise gráfica dos resíduos, o melhor desempenho para a forma do tronco das árvores foi observado no ajuste do modelo de Hadetzky (3), e para estimativa do volume total foi a equação (1) de Schumacher, tanto para o conjunto de dados total, quanto para as árvores quadráticas médias e dominantes.
O polinômio de potências (Hadetzky) e a equação de Schumacher, foram selecionados como os mais adequados para estimativa do volume das árvores de Pinus taeda, por apresentarem maior coeficiente de determinação ajustado, menor erro padrão da estimativa e ausência de tendenciosidade na distribuição de resíduos. Neste sentido, o modelo de Hadetzky e Schumacher são recomendados para tal uso para a espécies de Pinus taeda na região de estudo.
Em relação as três diferentes formas de ajuste (banco de dados total, árvores médias quadráticas e árvores dominantes), foi observado que os ajustes realizados com o banco de dados das árvores dominantes apresentaram valores superiores se comparado com as outras formas de ajuste, tanto para as funções de afilamento quanto para as equações de volume. A altura dominante (hdom) tem sido largamente usada no setor florestal, caracteriza-se por ser independente e pouco influenciada pelos tratos silviculturais. Além disso, existe boa correlação com a produção total em volume do povoamento (FINGER 2011; MACHADO e FIGUEIREDO FILHO, 2014).
As equações de volume se mostraram mais eficientes do que as funções de afilamento para a estimativa do volume total de Pinus taeda na região dos Campos Gerais, estado do Paraná.
O Polinômio de Potências Fracionárias de Hadetzky apresentou as melhores estatísticas entre as funções de afilamento na estimativa do volume total de Pinus taeda em todas as situações de ajuste avaliadas;
Para estimativa de volume total com casca de Pinus taeda, pelas equações de volume, o modelo de Schumacher se mostrou mais adequado em todas as situações de ajuste avaliadas.
As equações de volume são mais eficientes na estimativa do volume total de Pinus taeda em relação as funções de afilamento, no entanto não permitem a obtenção do volume por sortimento.
As árvores dg apresentaram menor afilamento do que as árvores dominantes, possivelmente pelo fato das árvores dg serem mais afetadas no interior da florestal o que denota-se que o aumento do densidade da floresta pode aumentar o fator de forma dos indivíduos
ASSMAN, E. L. (1970) The principles of Forest yield study. New York, Pergamon Press. 506 p.
AZEVEDO, T. L.; MELLO, A. A. de; FERREIRA, R. A.; SANQUETTA, C. R.; NAKAJIMA, N. Y. (2011) Equações hipsométricas e volumétricas para um povoamento de Eucalyptus sp. localizado na FLONA do Ibura, Sergipe. Revista Brasileira de Ciências Agrárias. Recife, v.6, n.1, p.105-112.
CAMPOS, J.C.C.; LEITE, H.G. (2013) Mensuração florestal: perguntas e respostas. 4ª Edição Viçosa: UFV, 605p.
COSTA, E. A.; FINGER, C. A. G.; SCHNEIDER, P. R.; HESS, A. F. (2016) Função de afilamento e sortimentos de madeira para Araucaria angustifolia. Revista Ciência Florestal, Santa Maria, v. 26, n. 2, p. 523-533, abr.-jun.
DRAPER, N.; SMITH, H. (1966). Applied regression analysis. New York: JohnWiley e Sons. 709 p.
EISFELD, R. L.; MELLO, A. A.; SANQUETTA. C. R.; WEBER. K. S. (2004) Avaliação de modelos polinomiais na estimativa de volume total e por sortimento de Pinus taeda. Brasil Florestal, n. 79, p. 9-15.
FINGER, C. A. G. (2011) Biometria Florestal. Santa Maria. Universidade Federal de Santa. 2011.
FINGER, C. A. G. (1992) Fundamentos da Biometria Florestal. Santa Maria: Ed. da UFSM. 269 p.
HUSCH, B; MILLER, C.L.; BEERS, T.E. (1982) Forest mensuration. 3. ed. New York: J. Willey & Sons. 397p.
KOHLER, S. V.; KOEHLER, H. S.; FIGUEIREDO FILHO, A. (2013) Modelos de Afilamento para Pinus taeda por Classes de Idade. FLORAM - Revista Floresta e Ambiente, p. 470-479.
KOHLER, S. V.; KOEHLER, H. S.; FIGUEIREDO FILHO, AFONSO.; ARCE, J. E.; MACHADO, S. A. (2016) Evolution of tree stem taper in Pinus taeda stands. Ciência Rural, v. 46, p. 1185-1191.
KOZAK, A.; MUNRO D. D.; SMITH J. H G. (1969) Taper functions and their application in forest inventory. Forestry Chronicle, Ottawa, v.45, n.4, p.278-283.
LEAL, F.A.; CABACINHA, C.D.; CASTRO, R.V.O.; MATRICARDI, E.A.T. (2015) Amostragem de árvores de Eucalyptus na cubagem rigorosa para estimativa de modelos volumétricos. Revista Brasileira de Biometria, v. 33, n. 1, p. 91-103.
MACHADO, S. A.; FIGUEIREDO FILHO, A. (2014) Dendrometria. 2a.ed. Guarapuava: Unicentro Editora. v. 1. 316p.
MÔRA, R. (2015) Funções de afilamento de forma variável e modelagem de efeitos mistos em fustes de Pinus taeda e Eucalyptus saligna. 277 f. Tese (Doutarado em Engenharia Florestal) – Universidade Federal do Paraná. Curitiba, PR.
MÜLLER, I. (2004) Forma de Tronco e Sortimentos de Madeira para Eucalyptus grandis Hill ex Maiden., Manejado em Alto Fuste, na Região Sudeste do Estado do Rio Grande do Sul. 166 f. Tese de Doutorado. Programa de Pós-Graduação em Engenharia Florestal, Santa Maria, RS.
NOGUEIRA, G. S.; LEITE, H. G.; REIS, G. G.; MOREIRA, A. M. (2008) Influência do espaçamento inicial sobre a forma do fuste de árvores de Pinus taeda L. Revista Árvore, Viçosa, v.32, n.5, p.855-860.
PELISSARI, A. L.; LANSSANOVA, L. R.; DRESCHER, R. (2011) Modelos volumétricos para Pinus tropicais, em povoamento homogêneo, no Estado de Rondônia. Pesquisa Florestal Brasileira (Impresso), v. 2011, p. 173-181,
PEREIRA, J. E. S.; ANSUJ, A. P.; MÜLLER, I.; AMADOR, J. P. (2005) Modelagem do volume do tronco do Eucalyptus grandis Hill ex. Maridem. In: Simpósio de Engenharia de Produção. 12., Bauru. Anais... Bauru: SIMPEP, 2005.
PIMENTEL, A. (2009) Funções de afilamento para Pinus caribaea var. hondurensis. 123 f. Dissertação (Mestrado) - Universidade Federal do Paraná, Setor de Ciências Agrárias, Programa de Pós-Graduação em Engenharia Florestal.
SCHRODER, T.; COSTA, E. A.; VALERIO, A. F.; LISBOA, G. S. (2015) Taper Equations for Pinus elliottii Engelm. in Southern Paraná, Brazil. Forest Science, v. 61, p. 311-319.
SILVESTRE, R.; BONAZZA, M.; STANG, M.; LIMA, G.C.P.; KOEPSEL, D.A.; MARCO, F.T.; CIARNOSCHI, L.D.; SCARIOT, R.; MORÊS, D.F. (2014) Equações volumétricas em povoamentos de Pinus taeda L. no município de Lages-SC. Nativa, v. 02, n. 01, 01-05.
SOUZA R. R.; NOGUEIRA G. S.; MURTA JUNIOR L. S.; PELLI E.; OLIVEIRA M. L. R.; ABRAHÃO C. P.; LEITE H. G. (2016) Forma de fuste de árvores de Eucalyptus em plantios com diferentes densidades iniciais. Scientia Forestalis, 44 (109):33-40.
TEO, S. J.; MARCON, A.; EHLERS, T.; BIANCHI, J. C.; PELOSO, A. NAVA, P. R.; COSTA, R. H. (2013) Modelos de afilamento para Pinus elliottii em diferentes idades, na região de Caçador, SC. Floresta, Curitiba, v.43, n.3, p.439-452.
TESHOME, T. (2005). A ratio method for predicting stem merchantable volume and associated taper equations for Cupressus lusitanica, Ethiopia. For. Ecol. Manage. 204 (2–3): 171–179.
THOMAS, C. A. CESAR M.; SCHNEIDER, P. R.; FINGER, C. A. G. (2006) Comparação de equações volumétricas ajustadas com dados de cubagem e analise de tronco. Ciência Florestal, Santa Maria, v. 16, n. 3, p. 319-327, jul./set.
YOSHITANI JUNIOR, M.; NAKAJIMA, N. Y.; ARCE, J. E.; MACHADO, S. A.; DRUSZCZ, J. P.; HOSOKAWA, R. T.; MELLO, A. A. (2011) Funções de afilamento para plantios desbastados de Pinus taeda. Floresta, Curitiba, v.42, n.1, p.169-176.
1. Eng. Florestal, Dr., Professor Adjunto I do Departamento de Engenharia Florestal da Universidade do Estado de Santa Catarina (UDESC), Centro de Ciências Agroveterinárias (CAV), Lages, Santa Catarina, Brasil. thiago.stepka@udesc.br
2. Eng. Florestal, Montenegro Indústria, Comércio e Transporte de Madeira S.A., Ponta Grossa, Paraná, Brasil. gilvanzenyjr@hotmail.com
3. Eng. Florestal, Dr., Professor Adjunto do Departamento de Engenharia Florestal da Universidade Federal do Sul da Bahia (UFSB), Itabuna, Bahia, Brasil. gerson.lisboa@gmail.com
4. Eng. Florestal, Mestrando em Engenharia Florestal da Universidade Federal do Mato Grosso (UFMT), Cuiabá, Mato Grosso, Brasil. clebsonlima10@hotmail.com
5. Eng. Florestal, Dr., Professor Adjunto do Departamento de Engenharia Florestal da Universidade Estadual do Centro-Oeste (UNICENTRO), Irati, Paraná, Brasil. vagneralexp@yahoo.com.br
6. Eng. Florestal, Me. Doutorando em Engenharia Florestal da Universidade Federal Paraná (UFPR), Curitiba, Paraná, Brasil. mailsonroik@hotmail.com