ISSN 0798 1015

Vol. 38 (Nº 19) Año 2017. Pág. 27

Ajuste de modelos de séries temporais para o preço de venda do metro cúbico da Accacia mearnsii De Wild stand (Acácia Negra) no Rio Grande do Sul

Adjust series models for temporary price of cubic meter of sale Accacia mearnsii De Wild stand (Black Acacia) in Rio Grande do Sul

Cleiton TIBULO 1; Jorge Antônio de FARIAS 2 ; Diego Bergonsi DE FARIAS 3; Henrique Jorgielewicz ROGOVSCHI 4; Paulo Cézar CHITOLINA 5; Rafael da Silva RECH 6; Tainá Oliveira do AMARAL 7; Vaneza De CARLI Tibulo 8

Recibido: 05/11/16 • Aprobado: 03/12/2016

Conteúdo

1. Introdução

2. Matérias e métodos

3. Análise dos resultados

4. Considerações finais

Referências bibliográficas

1. Introdução

O plantio de Accacia mearnsii De Wild stand (Acácia Negra), no estado do Rio Grande do Sul, Brasil, expressa grande importância socioeconômica. Segundo a AGEFLOR (2016) o estado tem aproximadamente 100 mil hectares plantados, sendo o único estado brasileiro a cultivar esta espécie florestal em escala comercial.

Os povoamentos estão concentrados em pequenas propriedades rurais tipicamente relacionadas à agricultura familiar e também em propriedades de maior extensão, na maioria das vezes de propriedade de empreendedores ou das empresas florestais.

A acácia negra, dentro do estado do RS, é largamente utilizada para a produção de lenha, carvão vegetal e tanino, extraído da casca da árvore. Já em âmbito internacional, a espécie é exportada na forma de cavaco (lenha branca) pelas empresas Seta e Tanac para fabricação de celulose.

No inicio da década de 2000 houve grandes incentivos ao plantio de acácia negra no Rio Grande do Sul e milhares de produtores investiram na cultura, uma vez que a tendência indicava que as exportações aumentariam. Entretanto, no cenário atual percebe-se uma desvalorização no preço da acácia e o descontentamento dos acacicultores.

De acordo com FARSUL (2016) os problemas começaram com a crise econômica internacional de 2008, que abalou os mercados da madeira do Japão, grande importador da acácia negra e, além disso, a crise foi agravada ainda mais pelo tsunami de 2012.

O cenário econômico existente impactou o valor repassado aos produtores de acácia negra, gerando um cenário de total desencanto com a cultura, os valores pagos, após 7 anos, não eram capazes de cobrir os custos com o financiamento para o plantio florestal, transformando os povoamentos de acácia negra em florestas de baixíssimo valor financeiro.

Desta forma torna-se estratégico o uso de modelos matemáticos que possam auxiliar na maximização dos lucros, ou minimização dos custos, já que há perspectiva de pequena margem de lucro ou até mesmo prejuízo por parte dos produtores e da própria indústria para os setores ligados a produção e comercialização da acácia negra. Esses modelos estatísticos segundo BATISTA (2009) tem a capacidade de analisar e descrever o comportamento da série, investigar o mecanismo gerador da série, fazer previsões de valores futuros e procurar periodicidades relevantes nos dados.  

Este estudo tem por objetivo ajustar modelos estatísticos de séries temporais a série de dados histórica do preço de venda do metro cúbico da acácia negra.

2. Matérias e métodos

Os dados em análise referem-se à série histórica do preço de venda da acácia negra, coletados mensalmente, no período compreendido entre junho de 2003 a junho de 2013. Foram obtidos junto a empresa Seta, totalizando 121 observações.

Os modelos a serem testados são os modelos SARIMA e Holt-Winters. A escolha destes modelos para previsão do preço de venda da acácia negra deu-se pela necessidade da escolha de modelos que trabalhassem com a componente tendência e/ou sazonalidade corriqueiramente presentes na série. Cabe ressaltar que será testada a correlação entre o preço de venda da acácia negra, preço do óleo diesel, preço da celulose e valor do dólar para os mesmos períodos da série histórica em estudo, na busca de investigar causas e efeitos entre as variáveis. Caso seja comprovada a influência entre as variáveis, novos modelos mais sofisticados que permitam a inclusão de variáveis exógenas serão testados, na busca do melhor modelo que se ajuste a série.

Para aplicação e estimação dos modelos Holt-Winters será utilizado o Software livre R e o Statistic 9.1.

2.1 Modelos SARIMA

Segundo MORETTIN e TOLOI (2004), o modelo SARIMA é um caso geral dos modelos propostos por BOX e JENKINS (1976), para o ajuste de série temporais estacionárias. Entretanto, quando há presença da componente sazonal nos dados, a classe de modelos é denominada SARIMA (p,d,q)(P,D,Q), dado por:

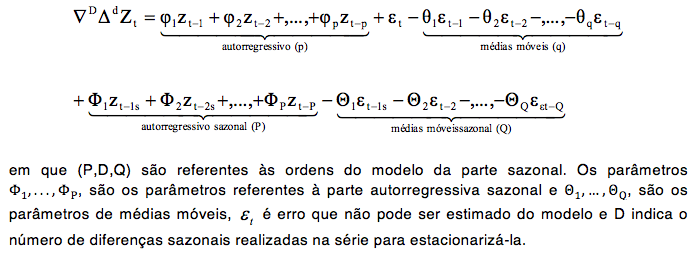
Segundo JUNIOR (2007), para um bom ajuste de um modelo de Box e Jenkins, é necessário que a estrutura residual seja um ruído branco, isto é, que o resíduo seja uma variável aleatória independente e identicamente distribuída,

Além disso, ACI (Akaike Information Criteria) e BIC (Bayesian Information Criterion) são utilizados para determinar a eficiência dos modelos ajustados.

Para determinar a eficiência dos modelos utilizar-se-á os critérios IAC e BIC. Os critérios de AIC proposto por AKAIKE (1974), e o BIC desenvolvido por AKAIKE (1978) são dados por:

Estes critérios levam em conta a variância do erro, o tamanho da amostra e os valores dos parâmetros estimados. Quanto menores forem estes valores melhor o ajuste do modelo e, por consequência, melhores serão as previsões.

2.2 Modelo de alisamento Holt-Winters

O modelo de alisamento exponencial de Holt-Winters pode ser divido em: modelo multiplicativo e modelo aditivo. A diferenciação do uso de um ou outro dependerá da componente sazonal da série.

Cada um dos procedimentos (aditivo ou multiplicativo) possui três constantes de alisamento diferenciadas (A, C e D), associadas a cada uma das componentes para sazonalidade, nível e tendência.

Os valores das constantes (A, C e D) são obtidos de modo que se obtenha a mínima soma dos quadrados dos erros de ajustamento das constantes de suavização.

Uma das vantagens do método é a aplicabilidade do processo sendo de fácil manipulação. Além de ser indicado para séries que apresentam tendências e sazonalidade.

2.2.1 Modelo aditivo

De acordo com VERÍSSIMO et al. (2012) e MORETTIN e TOLOI (2004), o modelo aditivo caracteriza-se pelo padrão sazonal não se alterar a medida que o nível da série muda. A equação geral do modelo é dada por:

para t=1, ..., N onde N é o tamanho da série.

As três equações de suavização são apresentadas abaixo:

onde A, C e D são as constantes de alisamento.

A equação de previsão(h) para o modelo aditivo é dada por:

2.2.2 Modelo multiplicativo

O modelo multiplicativo se caracteriza por ter a sazonalidade da série afetada pela tendência sendo o resultado do produto das componentes individuais e é representado pela seguinte equação, segundo VERÍSSIMO et al. (2012) e MORETTIN e TOLOI (2004):

para t=1,...,N onde N é tamanho da série.

As três equações de suavização são apresentadas abaixo:

onde A, C e D são as constantes de suavização, que são determinados pelos vetores (A, D, C), que minimiza os erros quadráticos de previsão, s corresponde ao valor de sazonal e N o número de observações.

A equação de previsão do modelo multiplicativo é dada por:

2.3 Critérios de seleção

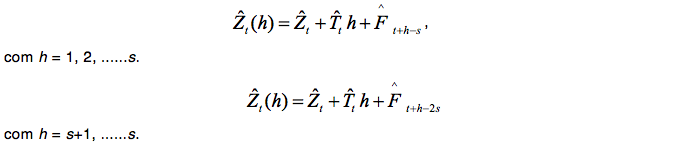
O ajuste e a escolha do melhor modelo visam possibilitar previsão de preços da acácia negra, que possa auxiliar produtores na comercialização do produto e demonstrar a necessidade de mais estudos na área. Entretanto, é de fundamental importância a utilização de critérios de seleção para a escolha dos melhores modelos.

Para isso serão reservadas as últimas seis observações da série histórica para fins de comparação com os valores previstos dos modelos ajustados.

Utilizar-se-á também dois critérios de avaliação: (MAD – mean absolute deviation) e (SSE – sum of square for forecast error).

3. Análise dos resultados

Para um melhor entendimento da variável valor de venda da acácia negra são apresentadas, na Tabela 1, algumas medidas descritivas.

O preço médio da acácia negra ao longo do tempo é de R$ 43,89 e apresenta um coeficiente de variação de 7,38%. Apesar de não possuir grandes oscilações em seu preço de venda como podemos perceber no valor do desvio-padrão. Esta variação pode significar a lucratividade para o produtor ou de agregar uma margem de lucro maior a seu produto final, trazendo maior rentabilidade a seu produto principalmente devido ao longo período de espera para a extração da madeira e subprodutos. Podemos perceber isso também na diferença entre o valor máximo e mínimo.

Tabela 1 - Medidas descritivas do preço de comercialização da acácia negra – RS, 2003 a 2013

De acordo com o previsto em metodologia testou-se a correlação entre as variáveis: Preço da Celulose, Valor do Dólar, Preço do Diesel e Preço da Acácia Negra.

A Tabela 2 mostra as correlações entre as variáveis. Onde pode-se observar que o Preço de Venda da Acácia Negra não está correlacionada com o preço da celulose, valor do dólar e preço do diesel. Já a celulose possui correlação positiva com o preço do diesel e correlação forte negativa com o preço do dólar indicando estudos futuros para esta variável.

Tabela 2: Correlação entre Preço Celulose x Dólar x Diesel x Acácia Negra

Como observado na Tabela 2, não se faz necessário utilizar as variáveis preço da celulose, dólar e diesel como variáveis exógenas aos modelos para a previsão do preço pago pelo metro cúbico da acácia negra. Confirmando as previsões inicias de ajustar modelos de suavização exponencial e os modelos SARIMA.

Para dar-se início ao ajuste do modelo, observa-se na Figura 1, o comportamento da série original buscando identificar suas componentes, como tendência e/ou sazonalidade.

Figura 1: Série Histórica do preço de venda do metro cúbico da acácia negra

Analisando-se a Figura 1, verifica-se que há indícios de que a série possui sazonalidade, não demonstrando presença de tendência, o que indica não ser necessário aplicar diferenciações na série original.

A decomposição da série original também permite identificar componentes importantes da série e confirmar se há presença de sazonalidade e/ou tendência. Considerando-se a Figura 2, pode observar-se, respectivamente, que a série não possui tendência, mas que possui sazonalidade.

Figura 2 - Decomposição da série temporal em componentes de sazonalidade, de tendência e de aleatoriedade

Os testes de Friedman e Kruskal Wallis, ambos com p-valor <0,05 comprovam a análise gráfica de que a série em estudo possui sazonalidade, justificando o uso dos modelos Holt-Winters e SARIMA.

Após esta etapa inicial foram construídos os gráficos das funções de autocorrelação amostral (ACF) e de autocorrelação parcial amostral (PACF), que estão apresentadas na Figura 3.

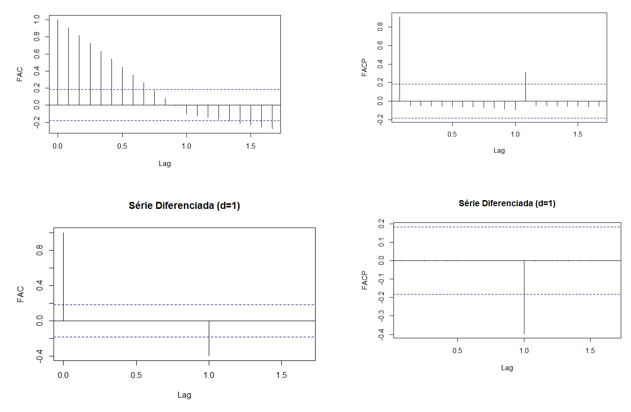
Figura 3 - Função de Autocorrelação (ACF) e Autocorrelação Parcial (PACF)

Os correlogramas apresentam as correlações seriais no domínio do tempo. Com base em suas frequências estimadas é possível verificar sazonalidades e ciclos na série. Na Figura 3 apresenta-se os correlogramas das séries, sem diferença, diferença de ordem 1. Os gráficos das ACF e PACF da série em nível apresentam correlação significativa nos primeiros lags decaindo exponencialmente, indicativos de um modelo autorregressivo.

Ao se analisar os ACF e PACF com diferença de ordem 1, percebe-se características de um modelo estacionário autorregressivo de ordem 1, não deixando claro a ordem da parte sazonal do modelo. Essa análise é sumária para dar início ao processo de modelagem. Cabe ressaltar que vários modelos de ordem diferentes aqui serão considerados e avaliados de acordo com os critérios de seleção sugeridos na metodologia.

Na Tabela 2 são apresentados alguns dos melhores modelos concorrentes ajustados para a série histórica do preço de venda do metro cúbico da acácia negra, com os respectivos valores de AIC e BIC.

Tabela 2 - Modelos concorrentes SARIMA e os respectivos critérios

Os parâmetros do modelo SARIMA ajustado para a série histórica estão na Tabela 3, com um parâmetro autorregressivo na parte ordinal e quatro parâmetro autorregressivo na parte sazonal e uma diferença na parte sazonal. Para estimar os parâmetros do modelo foi usado o software estatístico R.

Tabela 3 - Parâmetros do modelo selecionado

Reescrevendo o modelo SARIMA (p,d,q)(P,D,Q), e substituindo os valores dos coeficientes, temos:

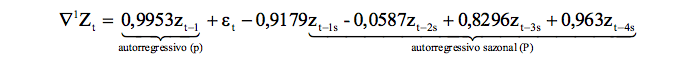
Após selecionado o modelo SARIMA (1,0,0)(4,1,0)12, por meio dos critérios de seleção AIC e BIC, analisou-se a condição de ruído branco (média zero, variância constante, erros descorrelacionados) do modelo.

Considerando-se a análise dos resíduos observou-se que média zero e variância constante. Nos gráficos de autocorrelação dos resíduos (Figura 4), é possível perceber que não há autocorrelação significativamente diferente de zero em nenhuma defasagem, indicando que os resíduos são independentes, concluindo-se que os pressupostos de ruído branco foram atendidos.

Figura 4 - Função de autocorrelação (ACF) e autocorrelação parcial dos resíduos (PACF)

Nesta etapa do trabalho foram traçadas previsões do preço de venda para o metro cúbico da acácia negra, para um horizonte de seis passos à frente, ou seja, meses que não foram considerados no ajuste do modelo. Na Figura 5 é demonstrada a série ajustada e a série real.

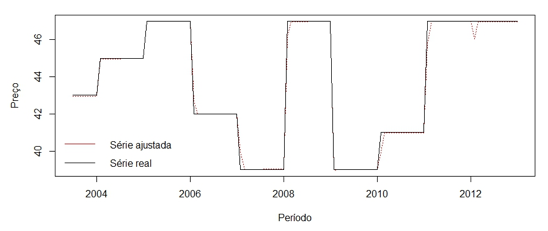
Figura 5 - Série ajustada (linha vermelha) dentro do período observado, e série observada (linha preta)

As previsões para o modelo ajustado SARIMA (1,0,0)(4,1,0)12 podem ser observadas na Tabela 5.

Tabela 5: Valores Previstos (h=6)

Na sequência conforme previsto na metodologia os modelos Holt-Winters Aditivo e multiplicativo serão ajustados a série histórica do preço do metro cúbico da acácia negra.

Considerando o modelo de alisamento exponencial de Holt-Winters, os valores das constantes de suavização que melhor se ajustaram para o modelo aditivo e multiplicativos estão expressos na Tabela 6.

Tabela 6: Constantes de Suavização

Tanto os modelos aditivo quanto multiplicativo atribuem maior peso a constante A, ligada ao fator sazonal.

Na Figura 6A, é possível observar os valores reais e previstos real e na Figura 6B a Série Ajustada e as previsões para o modelo aditivo. Os gráficos demonstram o bom ajuste do modelo, tanto no modelo aditivo quanto multiplicativo, as séries previstas e reais se subscrevem não sendo possível observar as duas em um mesmo gráfico.

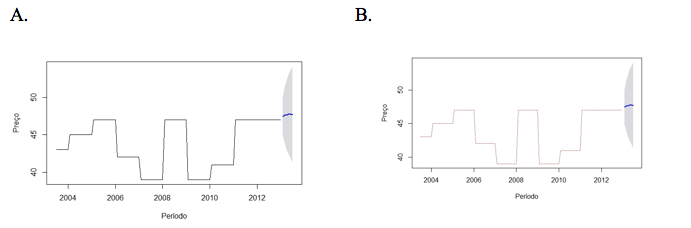
Figura 6: A. Série Real e Previsões Modelo Aditivo e B: Série Ajustada e Previsões Modelo Aditivo

A Figura 7, expressa os gráficos dos valores reais e ajustes e suas respectivas previsões do modelo multiplicativo.

Figura 7: A. Série Real e previsões Modelo Multiplicativo e B: Série Ajustada e Previsões Modelo Multiplicativo

Para o ajuste do modelo de alisamento exponencial Holt-Winters, foram testados os modelos aditivo e multiplicativo e comparados com a série real. Conforme previsto em metodologia foram reservados os últimos seis valores da série real para fins de comparação e verificação do ajuste do modelo. Os resultados da comparação entre o modelo aditivo e multiplicativo estão na Tabela 7, além dos respectivos valores para a série real.

Tabela 7: Valores Previstos (h=6)

O modelo Holt-hinters aditivo e multiplicativo se ajustam adequadamente a série Preço de venda da Acácia Negra conforme as (Figuras 6 e 7). Para escolha do melhor modelo será utilizado os critérios de avaliação MAD e SSE, os resultados encontrados estão expressos na Tabela 8.

Tabela 8: Comparação dos modelos

De acordo com os critérios utilizados para a escolha do melhor modelo, o modelo multiplicativo possui menores valores de MAD e SSE, demonstrando que a série prevista está mais próxima a série real em relação aos seus concorrente Holt-Winters aditivo e SARIMA (1,0,0)(4,1,0)12. Desta forma, o modelo multiplicativo apresenta melhores valores de previsão para a série histórica do preço de venda do metro cúbico da acácia negra.

4. Considerações finais

Observou-se que a série histórica do preço da acácia negra possui movimentos cíclicos com períodos em que os valores se aproximam do valor máximo R$ 49,00 e períodos próximos aos valores mínimos em torno de R$ 37,00. Estas oscilações apesar de ocorrem em períodos longos podem ocasionar enormes prejuízos aos acacicultores pois podem estar atrelados a períodos de entre safra. Apesar da série em estudo não possuir grande variabilidade, há de se considerar que os produtores estão trabalhando no limite entre o lucro e o prejuízo. Sendo assim, é de fundamental importância a estimação de valores futuros na busca de melhores resultados de venda e tomadas de decisão.

Quando a influência das variáveis preço do dólar, celulose e diesel, constatou-se que para essa série em análise essas varáveis não ocasionaram causa e efeito, desta forma não influenciam diretamente no preço pago para a acácia negra.

No ajuste de um modelo a série histórica verificou-se que os modelos (Holt-Winters) tanto aditivo, quanto multiplicativo, adequaram-se positivamente a série e apresentaram resultados satisfatórios de previsões. Por serem de fácil manipulação, entendimento e demonstrarem bons resultados devem ser considerados para previsão de valores futuros da acácia negra. O melhor modelo SARIMA (1,0,0)(4,1,0)12,  apesar de ajustar-se a série em estudo ficou aquém de seu concorrentes em estudos futuros será testado em outras séries históricas.

Fica evidente neste trabalho, que séries temporais podem ser usadas para previsão de preços de comercialização de produtos. Desta forma, não só para o mercado da acácia negra, mas também para outras culturas, esses modelos podem auxiliar na previsão de valores futuros, oferecendo condições ou embasando aos produtores em suas tomadas de decisões quanto ao melhor momento de comercializar os produtos.

Referências bibliográficas

AGEFLOR (Rio Grande do Sul). A Indústria de Base Florestal no RS: Dados e Fatos. 2016. Disponível em: <http://www.ageflor.com.br/noticias/wp-content/uploads/2016/09/AGEFLOR-DADOS-E-FATOS-2016.pdf>. Acesso em: 22 set. 2016.

Akaike, H. A. (1974); “A new look at the statistical model identification. IEEE Transactions on Automatic Control”, v.19, n.6, p.716-723.

Akaike, H. A (1978); “Bayesian analysis of the minimum AIC procedure”. Annals of the Institute of Statistical Mathematics, Tokyo, v.30, p.9- 14.

Batista, A. L. F. (2009); “Modelos de séries temporais e redes neurais na previsão de vazão”, 2009, 79 f. Dissertação de Mestrado (Mestrado em Engenharia de Sistemas) – Universidade Federal de Lavras, Lavras.

FARSUL, RIO GRANDE DO SUL . Farsul e Ageflor debatem mercado para acácia negra. Jornal em Formato HTML nº 396, 30 de setembro de 2016. Disponível em: <http://www.sulrural.com.br/edicoes_anteriores_html2.php?idjorhtml=3053&idjor=94>. Acesso em: 18 Set. 2016.

JUNIOR, A. M. (2007); “Análise de métodos de previsão de demanda baseados em séries temporais em uma empresa do setor de perfumes e cosméticos”, 2007, 100 f. Dissertação de Mestrado (Mestrado em Engenharia de Produção) – Pontifícia Universidade do Paraná, Curitiba.

Morettin, P. A.; Toloi, C. M. C. (2004); Análise de Séries Temporais. São Paulo: Edgard Blucher LTDA, 535 p.

VERÍSSIMO, A. J.; ALVES, C. C.; HENNING, E.; AMARAL, C. E.; CRUZ, A. C.(2012); Métodos estatísticos de suavização exponencial Holt-Winters para a previsão da demanda em uma empresa do setor metal mecânico. Revista Gestão Industrial, v.8, n.4, p. 154-171.

1. Pós-Graduando em Estatística e Métodos Quantitativos Universidade Federal de Santa Maria, Santa Maria-RS, Brasil. E-mail: tibulo_cleiton@hotmail.com

2. Prof. Dr. do Departamento de Ciências Florestais da Universidade Federal de Santa Maria, Santa Maria-RS, Brasil.

3. Granduando em Relações Internacionais da Universidade Federal de Santa Maria, Santa Maria-RS, Brasil

4. Granduando em Relações Internacionais da Universidade Federal de Santa Maria, Santa Maria-RS, Brasil;

5. Engenheiro Florestal da Empresa Seta S. A;

6. Graduando em Engenharia Florestal da Universidade Federal de Santa Maria, Santa Maria-RS, Brasil;

7. Graduanda em Ciências Econômicas da Universidade Federal de Santa Maria, Santa Maria-RS, Brasil;

8. Doutoranda em Educação em Ciências: Química da Vida e Saúde da Universidade Federal de Santa Maria, Santa Maria-RS, Brasil. E-mail: Vaneza_dc@yahoo.com.br