ISSN 0798 1015

Vol. 38 (Nº 15) Año 2017. Pág. 15

Abordagem contextualizada do método Runge-Kutta na disciplina de Cálculo Numérico para Engenharia

A physics approach with Runge-Kutta´s method in numerical calculus discipline

P. FREITAS-LEMES 1; D. C.VILELA 2; J.S.E. GERMANO 3

Recibido: 17/10/16 • Aprobado: 15/11/2016

Conteúdo

1. Introdução

2. O Runge-Kutta e a queda de uma partícula

3. Metodologia

4. Resultados

5. Considerações Finais

Agradecimentos

Referências

1. Introdução

O cálculo numérico é constituído de técnicas matemática utilizadas para solucionar problemas matemáticos que não podem ser resolvidos ou que são difíceis de resolver de forma analítica. Segundo Chapra (2010), o cálculo numérico é o conjunto de técnicas pelas quais os problemas matemáticos são formulados de modo que possam ser resolvidos com operações aritméticas. Embora existam muitos tipos de métodos numéricos, eles têm uma característica comum: invariavelmente, envolvem um grande número de cálculos aritméticos tedioso. Não é de admirar que, com o rápido e eficiente desenvolvimento dos computadores, o papel do cálculo numérico na resolução de problemas de engenharia aumentou drasticamente nos últimos anos.

Muitas das técnicas estudadas na disciplina de Cálculo Numérico foram desenvolvidas há muitos anos e implementadas com dificuldade devido aos recursos computacionais da época. Este fato limitava a quantidade de cálculos realizados, prejudicando assim a precisão da solução. Atualmente o acesso a eficientes computadores é fácil e as técnicas do Cálculo Numérico podem ser utilizadas em computadores rápidos e que produzem soluções precisas (Santos, 2010). De acordo com Wenjiang (2009) experiências ao longo dos anos, ministrando esta disciplina, mostraram que a aprendizagem do Cálculo Numérico se mostra mais eficiente e atrativa ao aluno quando contextualizada e resolvida com o auxílio de computadores.

Ensinar de modo eficiente, tornando a aprendizagem significativa e relacionando-a com aplicações na sua futura área de atuação deve ser uma preocupação constante, já que esses fatores estão estreitamente ligados com o índice de evasão nas universidades. Dentre os fatores que levam o aluno a evadir, são bem explicitados o baixo desempenho, o descontentamento com a didática, o currículo não condizente com as condições do mercado e problemas relacionados à falta de estrutura e de metodologias (Gaioso, 2006).

Gerab (2016) aponta que a evasão nos dois primeiro anos do curso de engenharia corresponde a mais de 60% da evasão do curso todo. Um dos pontos sugeridos pelos alunos evadidos é uma atenção maior na interação entre teoria e prática, aumentando as possibilidades de motivar os alunos por intermédio das práticas que aproximem a realidade do pensamento teórico (Freitas, 2016).

Entre as disciplinas tidas como teóricas, que estão nas séries iniciais da engenharia, encontramos o Cálculo Numérico, onde em muitos casos o ensino é descontextualizado e os métodos são apresentados com tabelas prontas, sem apresentar a importância ou a função em situações reais.

A disciplina de Cálculo Numérico habitualmente é ministrada em um curso de 72horas/ aula, ao longo do segundo ano do curso de engenharia. A ementa inicia em métodos para se encontrar o “zero da função” e chega a técnicas de resolução de uma Equação Diferencial, como o método do Runge-Kutta, por exemplo. Pensando em como aprimorar o ensino-aprendizagem desta disciplina, associando o uso de técnicas computacionais, a contextualização do tópico estudado, e se adequando a quantidade de aulas disponível para este tópico, criamos uma proposta de ensino usando o problema da queda livre.

O problema da queda é conhecido dos alunos, comumente estudado na disciplina de Física Teórica e Experimental, ao longo do primeiro ano da graduação. Nesta disciplina, como o aluno não sabe resolver uma equação diferencial, a resistência do ar é na maioria das vezes desprezada. Quando o aluno está cursando a disciplina de Cálculo Numérico e aprende o método de Runge-Kutta, ele adquire conhecimento suficiente para resolver esse problema de forma mais fidedigna, acrescentando a força resistiva do ar.

A presente proposta foi aplicada em 42 alunos do segundo ano do curso de Engenharia da Universidade do Vale do Paraíba - UNIVAP. Para avaliar o ganho educacional alcançado pelos alunos após essa intervenção, usamos o parâmetro D de Cohen (Cohen, 1992). Para se mensurar esse parâmetro, usando a técnica do pré-teste e do pós-teste (Gery, 1972).

O coeficiente D de Cohen (Cohen, 1977) é usado para estimar o tamanho do efeito da intervenção fornecida para os participantes do grupo experimental (COHEN, 1977; HALLAHAN et al., 1996; LOO KANG et al., 2015). O ganho educacional alcançado é calculado pelo método:

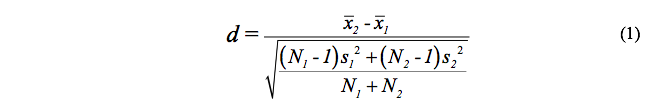
onde:

X₁: média de acertos das questões do pré-teste;

X₂: média de acertos das questões do pós-teste;

N₁: número de alunos que realizaram o pré-teste;

N₂: número de alunos que realizaram o pós-teste;

s1: desvio padrão dos acertos das questões do pré-teste;

s2: desvio padrão dos acertos das questões do pós-teste.

Outro parâmetro utilizado para se mensurar o ganho alcançado foi o <g> ganho educacional. Gery (1972) propôs o cálculo do ganho educacional medido como uma variável dependente das médias obtidas:

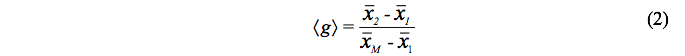
 é a nota máxima que o aluno pode alcançar. Os valores deste ganho foram analisados por Hake (1998, 2002) que classificou os seus valores em:

Ganho baixo <g> <0,30;

Ganho Médio 0,30 < <g> < 0,70; e

Ganho Alto: <g> > 0,70.

Com isso, é objetivo deste trabalho apresentar os resultados obtidos com a aplicação de uma proposta de ensino para Engenharia que mostra a aplicação do algoritmo de Runge-Kutta no problema da queda de uma partícula. A eficiência da intervenção didática foi medida usando os parâmetros D de Cohen e o <g> ganho educacional.

2. O Runge-Kutta e a queda de uma partícula

2.1. O Método de Runge-Kutta

O algoritmo de Runge-Kutta é um tópico fundamental abordado na disciplina de Cálculo Numérico para a Engenharia, é composto por métodos iterativos implícitos e explícitos empregados na resolução numérica de Equações Diferencias Ordinárias, Lineares e não lineares. Estas técnicas foram desenvolvidas por volta de 1900 pelos matemáticos C. Runge e M.W. Kutta (Chapra, 2010).

2.2. A Queda de uma partícula

Movimento de queda de uma partícula no ar é um tema vastamente trabalhado nas séries inicias da Engenharia, tanto do ponto de vista teórico quanto experimental.

Para a contextualização desse problema na perspectiva da utilização do Runge-Kutta, consideramos a seguinte situação: uma partícula de massa m é solta a partir de uma altura H, como ilustra a Figura 1, onde além da força peso iremos consideradar que a partícula sofre a influência de uma força resistiva proporcional a velocidade devido ao ar. Para analisar a situação proposta, vamos primeiro apresentar a bem conhecida solução do movimento sem considerar a força resistiva. Para esse situação podemos escrever a partir da segunda lei de Newton:

          Figura 1: Ilustração do problema.

Considerando agora que a partícula se move no ar, e que o ar produz uma força resistiva proporcional a velocidade que se opõe ao movimento, podemos reescrever a segunda lei de Newton da seguinte forma :

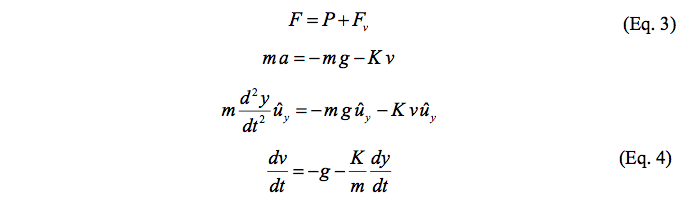
Assim, temos a equação diferencial linear, que será resolvida numericamente e sua solução comparada com o resultado experimental.

2.3. O Runge-Kutta aplicado ao problema da queda de uma partícula

Para solucionar o modelo descrito pela Equação 4, será utilizado o método numérico de Runge-Kutta de quarta ordem. Este método discretiza a função em passos de tempo (ℎ), repetindo-a até um instante pré determinado. A partir da solução o aluno consegue entender como se comporta a trajetória, velocidade e aceleração da partícula estudada.

3. Metodologia

Este projeto foi aplicado em 42 alunos do segundo ano do curso de Engenharia da Universidade do Vale do Paraíba – UNIVAP, situada em São José dos Campos, SP. A duração do projeto foi de 12 aulas, sendo o tempo dividido em três etapas: (I) 3 aulas teóricas, (II) 7 aulas experimentais e (III) 2 aulas utilizadas para a aplicação dos testes (veja Tabela 1)

Tabela 1: Cronograma das atividades.

Etapa I: Aulas teóricas: Foi apresentado aos alunos o método do Runge-Kutta através da demonstração da fórmula e os passos de resolução para uma equação diferencial qualquer. Após a explicação e a resolução de um exemplo pela professora, os alunos trabalharam em grupos para a resolução de diferentes equações diferenciais propostas usando os meios tradicionais, como mostra a Figura 2.

Figura 2: Alunos durante as aulas teóricas resolvendo as equações
diferenciais usando o método Runge-Kutta através dos meios tradicionais.

Etapa II: Aulas Experimentais: Nas aulas experimentais os alunos usaram o software Tracker® (BROWN, 2009) para fazer a captura dos dados e o software Microsoft Excel® para resolver o Runge-Kutta. Adotou-se o software Tracker®, por ser um software gratuito e que rastreia o movimento de qualquer objeto, possibilitando ao aluno estudar ponto a ponto a sua trajetória. Este software é gratuito, podendo ser instalado e executado em plataformas como Windows, Linux e Mac, disponível em alguns idiomas, inclusive em português. Possui resultados com design visual e não matemático, interatividade, feedback instantâneo e interpretação de videoanálises intuitivas.

Em um primeiro momento os alunos auxiliaram na parte experimental, isto é, a soltar uma bolinha de uma altura conhecida e analisar usando o Tracker® (veja Figura 3a). Depois os alunos deveriam plotar no mesmo gráfico o resultado experimental e o teórico sem considerar o efeito da força resisitiva, e comparar os resultados, como mostra a Figura 3b.

Figura 3: (a) Aluno soltando uma bolinha durante a aula experimental.
(b) Gráfico comparativo mostrando a diferença encontrada entre os pontos experimentais (Verde)
e o modelo teórico que despreza a resistência do ar (Vermelho).

Uma discussão sobre qual o valor que K (coeficiente de resistência do ar) deveria assumir foi realizada e um valor, previamente calculado, usando o software Mathematica® (WOLFRAM,2003), foi fornecido aos alunos.

Com todos os parâmetros que compõem a equação diferencial que descreve o problema, os alunos seguiram para o laboratório de informática e resolveram a equação usando o Excel®, veja na Figura 4 uma das soluções feita pelos alunos.

Etapa III: Testes: Na execução do projeto dois testes foram aplicados e o ganho educacional alcançado pela turma foi calculado usando o método desenvolvido por Cohen (1977, 1992), onde foi possível identificar o avanço dos alunos ao logo dessa proposta de ensino.

Ambos os testes (denominados pré-teste e pós-teste) tinham 5 questões, com a finalidade de avaliar o conhecimento dos alunos na parte teórica do problema da queda de uma partícula e, o ganho proporcionado pelas aulas experimentais.

As questões do pré-teste e do pós-teste eram similares. A primeira questão abordava o conhecimento do aluno sobre o comportamento gráfico das variáveis: trajetória, velocidade e aceleração. A segunda questão relacionava a posição de uma partícula lançada para cima e que retorna ao solo, sob o efeito da gravidade. A terceira questão contempla a relação entre a aceleração e o tempo de uma partícula que muda de sentido. A quarta questão apresenta um gráfico com duas trajetórias com uma tênue diferença, referente à ação da resistência do ar, ponto que os alunos deveriam identificar. A quinta, e última questão, era uma equação diferencial semelhante à Equação 4, onde os alunos deveriam resolver com h = 0,1 no pré-teste, usando meios tradicionais e com h = 0,01 no pós-teste com o auxílio do computador.

Figura 4: (a) Planilha do Excel® de um dos alunos com uma das soluções da Equação Diferencial
usando o método de Runge-Kutta de quarta ordem com passo de 0,01.
(b) Gráfico comparativo mostrando a solução da Equação Diferencial usando o Runge-Kutta (Azul).

4. Resultados

Com base nas notas obtidas no pré e pós-teste realizado com os alunos do curso de engenharia fizemos a análise do ganho educacional alcançado. Para o pré-teste a média alcançada foi de x₁= (3,167±1,308) e para o pós-teste foi x₂ = (3,813±1,012).

Para a análise do ganho educacional obtido pelos alunos ao longo da prática de laboratório, usamos o parâmetro D de Cohen (Cohen, 1992), que com base nos dados obtidos corresponde a D=0,55, que corresponde a um ganho educacional médio segundo Cohen. Na Figura 5 é apresentada a distribuição de frequência de notas dos alunos no pré e pós-teste. Podemos observar pelo gráfico que houve uma evolução das notas após a inserção dessas novas estratégias que usam outras tecnologias.

Wee (2015) aplicaram o uso das novas tecnologias no estudo de queda livre e lançamento vertical “toss up” para alunos do Ensino Médio. Durante três semanas eles fizeram a inserção do Tracker® nas aulas de física e o ganho educacional foi de D=0,79, considerado grande.

Para este projeto nós consideramos que o ganho educacional foi satisfatório e introduziu não só um avanço nas notas, mas também na relação dos alunos com a resolução do Runge-Kutta. A participação das aulas experimentais e a visualização da utilidade deste método trouxeram a disciplina de Cálculo Numérico uma maior aceitação por parte dos alunos, segundo os próprios alunos relataram em conversas informais após a aula.

A importância da utilização de laboratórios e de aulas experimentais não é algo novo, entretanto, na disciplina de Cálculo Numérico ainda são raros os casos de aplicação. Segundo Aguiar (1999), não se pode negar que o laboratório surgiu para complementar a teoria ou dar sentido à mesma e que a teoria não pode estar distante da prática, precisa haver uma união entre as duas.

Figura 5: Distribuição de frequência das notas do Pré e Pós-teste.

5. Considerações Finais

A realização desta proposta de ensino, apesar do pouco para a sua aplicação, nos mostrou um caminho interessante e viável de ser aplicado em uma disciplina de Cálculo Numérico. A associação da tecnologia oferecida pelo software Tracker® com a eficácia do algoritmo de Runge-Kutta se mostrou eficiente para fornecer ao aluno condições de: (1) mensurar a trajetória e a velocidade da partícula colocada em queda, o que o ajudou a compreender e sanar possíveis lacunas que ainda possam ter restado; (2) perceber a utilidade do método Runge-Kutta, mostrando a aplicabilidade em problemas simples e complexos tanto da Física como de áreas afins, e (3) tornar a aula mais dinâmica, sem perder o ganho educacional, como mostra a Figura 5.

Figura 6 – Diagrama de correlação entre o ganho educacional e os testes aplicados.

O gráfico tridimensional da Figura 6 apresenta a relação entre o Pré-Teste (x), o Pós-Teste (y) e o ganho educacional <g> (z) de cada aluno da turma analisada. A escala de cor mostra em branco os que tiverem maior ganho e em vermelho, os que tiveram menor avanço.

O resultado mostrou-se positivo com essa abordagem de ensino, nos apontando uma saída interessante para uma elaboração de propostas futuras que contemplem aulas práticas também nas disciplinas tidas como teóricas. Trabalhos semelhantes a esse podem ser aplicados, por exemplo, na disciplina de Equações Diferenciais usando o experimento do pêndulo simples, entre outros. Ou ainda, na própria disciplina de Cálculo Numérico, incorporando outras situações problema, já que o Runge-Kutta resolve todos os tipos de Equações Diferenciais.

Por fim, podemos observar que a combinação das aulas teóricas com a prática favorece o entendimento do assunto estudado pelos alunos, e, assim como relatado por Medeiros (2009), com a intervenção das aulas práticas os alunos despertam atitudes investigativas acerca do assunto e, consequentemente, apresentam melhora no seu rendimento acadêmico.

Agradecimentos

P. FREITAS-LEMES agradece a CAPES pelo apoio financeiro.

Referências

AGUIAR, M. Uma ideia para o laboratório de Matemática. Dissertação de Mestrado. São Paulo: USP, 1999.

BROWN, D. Videos Modeling with Tracker, presented at the American Association of Physics Teachers AAPT Summer Meeting, Ann Arbor, 2009.

CHAPRA, Steven C. Numerical methods for engineers. Hardcover. 6th ed. 2010.

COHEN, J. Statistical power analysis for the behavioral sciences (rev. ed.). Academic Press. New York, p. 357-410,  1977.  

_________ A power primer. New York University. Psychological Bulletin, 112, 155‐159. 1992.

FREITAS, B. CANUTO, E. PEREIRA, C. Fatores da evasão discente no curso de engenharia civil da universidade estadual da Paraíba. COBENGE, 2016.

GAIOSO, N. P. de L. O Fenômeno da evasão escolar na educação superior no Brasil. Brasília: 2005. Projeto Permanência e Êxito do educando no CEFET/SC. Florianópolis, dezembro de 2006.

GERAB, F. Cálculo da evasão e do índice de titulação em cursos usando uma abordagem probabilística. COBENG. 2016.

GERY, F. W. Does mathematics matter? Research papers in economic education, p. 142-157, 1972.  

HAKE, R. R. Interactive-engagement versus traditional methods: A six-thousand-student survey of mechanics test data for introductory physics courses. American journal of Physics, v. 66, n. 1, p. 64-74,  1998. 

_________Relationship of individual student normalized learning gains in mechanics with gender, high-school physics, and pretest scores on mathematics and spatial visualization. Physics Education Research Conference (Boise), ID, 2002.

HALLAHAN, M.; ROSENTHAL, R. Statistical power: Concepts, procedures, and applications. Behaviour research and therapy, v. 34, n. 5, p. 489-499, 1996. ISSN 0005-7967.

LOO KANG, W.  et al. Using Tracker to understand ‘toss up’ and free fall motion: a case study. Physics Education, v. 50, n. 4, p. 436,  2015.

MEDEIROS, E. Importância Das Aulas Experimentais No Ensino De Química. 14ºEPQA. 2009.

SANTOS, R. Álgebra Linear e Aplicações. Belo. Horizonte: Imprensa Universitária da UFMG, 2010.

WENJIANG, L. DONG, N. e FAN, T. “Application of Scilab in teaching of engineering numerical computations”. In: Open-source software for Scientific Computation (OSSC), IEEE International Workshop on. IEEE. 2009, pp. 88–90.

WEE L. K., TAN, S., LEONG, T. K., TAN, C. Using Tracker to understand ‘toss up’ and free fall motion: a case study. Phys. Educ. 50. 436. 215

WOLFRAM, S. The Mathematica® Book. Wolfram Media. ISBN1-57955-022-3, 2003.

1. ITA - Instituto Tecnológico de Aeronáutica. UNIVAP – Universidade do Vale do Paraíba - São José dos Campos – SP. Email: piprisc@gmail.com

2. ITA - Instituto Tecnológico de Aeronáutica - São José dos Campos – SP.

3. ITA - Instituto Tecnológico de Aeronáutica - São José dos Campos – SP.