ISSN 0798 1015
ISSN 0798 1015
Vol. 38 (Nº 10) Año 2017. Pág. 1
Eduardo Alexander DUQUE Grisales 1; Juan David GONZALEZ Ruíz 2; John Dairo RAMÍREZ Aristizabal 3
Recibido: 09/09/16 • Aprobado: 25/10/2016
4. Resultados y validez del modelo
RESUMEN: Un aspecto importante en la gestión operativa universitaria es la correcta utilización de sus recursos académicos en la programación de clases durante cada semestre. Para ello, es indispensable contar con un sistema confiable de asignación de aulas para los distintos cursos que ésta ofrece. Este trabajo se centra en la aplicación de un modelo de programación lineal para la asignación de aulas que minimice los costos ociosos de la Institución Universitaria Esumer y optimice los recursos académicos a utilizar. Para ello, es implementado y evaluado un modelo de programación lineal a través del software @Risk, y este se compara con el método manual de asignación de aulas de la institución. El modelo propuesto permite obtener soluciones eficientes en un tiempo de cálculo corto cumpliendo con todas las restricciones del modelo y minimizando la capacidad ociosa de las aulas. |
ABSTRACT: An important aspect in university operational management is the correct use of academic resources in programming classes each semester. It is therefore essential to have a reliable system for allocation of classrooms for different courses offered. This paper focuses on the application of a linear programming model for the allocation of classrooms to minimize Institución Universitaria Esumer´s idle costs and optimize its resource use. To do this, a linear programming model through @Risk software is implemented and evaluated. Then, it is compared with the manual method of classroom assignment in the institution. The proposed model helps obtaining efficient solutions in a short calculation time meeting all the limitations of the model and minimizing idle capacity in the classrooms. |
La asignación de aulas en una Institución de Educación Superior es un problema complejo debido a la cantidad de restricciones que presenta y el criterio con el que se aplican. Estas tareas por lo general requieren de mucho tiempo y en ocasiones genera pérdidas para la institución al asignarlas de una manera no sistémica o programada. Este trabajo busca principalmente la resolución de un problema práctico para la asignación de aulas en la Institución Universitaria Esumer de la ciudad de Medellín, con el fin de disminuir los costos ociosos que se presentan al interior de la misma, debido a la falta de una programación eficiente y acertada de los espacios disponibles en la institución.
El artículo se ha estructurado de la siguiente manera: una primera parte correspondiente a esta introducción. Posteriormente, se presenta una revisión literaria en la que se abordan los conceptos básicos de modelos de programación lineal y su uso en la asignación de recursos académicos. Posteriormente se presenta la metodología de estudio, en donde se describe el procedimiento para calcular las variables del modelo y su aplicación en el caso de estudio. Seguidamente se presentan los resultados de la investigación y las conclusiones obtenidas.
La literatura existente sobre el problema de asignación de aulas en instituciones de educación superior ha sido bastante amplia y bien documentada por diversos autores. Dammak, Elloumi y Kamoun (2007), Daskalaki, Birbas y Housos (2004), Hernández, Miranda y Rey (2008), Saldaña, Oliva y Pradenas (2007), Yakoob y Sherali (2007), y Soria‐Alcaraz, et al. (2011) resaltan el diseño y uso de modelos de programación lineal que permiten optimizar el problema de la asignación de espacios, a través de una función objetivo basada en el costo y el cumplimiento de ciertas restricciones específicas según el caso de estudio.
La utilización de modelos más complejos para la solución del problema en cuestión también ha sido objeto de estudio; Smith, Abramson y Duke (2003) desarrollaron un modelo a partir de redes neuronales, Caballero (2008) propuso un modelo mediante algoritmos evolutivos, Shiau (2011) aplicó el algoritmo de enjambre de partículas y Crovo, San Martín, & Rojas (2007) desarrollaron un modelo de programación entera para la asignación de aulas y horarios de clases universitarias.
La programación ha sido uno de los enfoques cuantitativos utilizado para la toma de decisiones en la administración. Se han reportado numerosas aplicaciones en ingeniería industrial y en sectores como educación, industrias químicas, del aerotransporte, del acero, del papel, del petróleo, entre otras.
A continuación, se describe el modelo de Programación Lineal a utilizar:
Variables
m = cantidad de aulas disponibles en cada jornada
n = cantidad de grupos a programar en cada jornada
Ki = capacidad del aula i en términos de sillas disponibles 
Cj= cantidad de alumnos del grupo j 
La capacidad disponible de cada aula (en # sillas) se puede obtener del área que administra los recursos en la institución, y la cantidad de alumnos de cada grupo, al igual que el número de grupos a programar se obtiene mediante un estimado que realiza el coordinador de programa, con esto establecemos una función de costos representada por las sillas ociosas que quedan en una determinada aula cuando se le asigna un determinado grupo, y se puede representar por la siguiente expresión
2.2. Función Objetivo
La función objetivo consiste en minimizar el número de sillas disponibles en la asignación y esto se representa con la siguiente expresión
Para la realización del proceso de asignación de aulas, se utilizó la información suministrada por la Institución Universitaria Esumer concerniente al número de aulas que dispone con su respectiva capacidad expresada en número de sillas. En la tabla 1 se muestra el listado de aulas con su codificación interna y la capacidad considerando el número de sillas disponibles que tiene cada aula.
Tabla 1: Aulas disponibles con su respectiva codificación y capacidad.
AULA |
CODIFICACION INSTITUCIONAL |
CAPACIDAD (# DE SILLAS) |
1 |
2-301 |
30 |
2 |
2-302 |
30 |
3 |
2-303 |
30 |
4 |
2-304 |
30 |
5 |
2-305 |
30 |
6 |
2-306 |
30 |
7 |
2-307 |
30 |
8 |
2-308 |
30 |
9 |
2-309 |
30 |
10 |
2-401 |
30 |
11 |
2-402 |
30 |
12 |
2-403 |
30 |
13 |
2-404 |
30 |
14 |
2-405 |
30 |
15 |
2-406 |
30 |
16 |
2-407 |
30 |
17 |
2-408 |
30 |
18 |
2-409 |
30 |
19 |
3-101 |
40 |
20 |
3-102 |
40 |
21 |
3-103 |
40 |
22 |
3-104 |
40 |
23 |
3-201 |
40 |
24 |
3-202 |
40 |
25 |
3-203 |
35 |
26 |
3-204 |
35 |
27 |
3-205 |
40 |
28 |
3-206 |
40 |
29 |
3-207 |
40 |
30 |
3-208 |
40 |
31 |
3-209 |
20 |
32 |
3-301 |
40 |
33 |
3-302 |
40 |
34 |
3-303 |
40 |
35 |
3-304 |
30 |
36 |
3-305 |
30 |
37 |
3-306 |
30 |
38 |
3-307 |
40 |
39 |
3-308 |
40 |
40 |
3-309 |
20 |
41 |
3-401 |
40 |
42 |
3-402 |
40 |
43 |
3-403 |
35 |
44 |
3-404 |
40 |
45 |
3-405 |
40 |
46 |
3-406 |
35 |
En esta tabla se muestra el número de aulas disponibles, la codificación interna y respectiva capacidad expresada en número de sillas con las que cuenta cada uno de los espacio. Fuente: Elaboración propia.
La Institución cuenta actualmente con tres jornadas académicas, la jornada diurna, nocturna y sabatina. En la tabla 2 se presentas las tres jornadas con sus respectivos horarios.
Tabla 2: Jornadas académicas con su codificación y horario.
# DE JORNADA |
CODIFICACION |
HORARIO |
1 |
Diurna |
Lunes a viernes de 06:00 a 12:00 horas |
2 |
Nocturna |
Lunes a viernes de 18:00 a 22:00 horas |
3 |
Sabatina |
Sábados de 06:00 a 18:00 horas |
En esta tabla se muestra el número de jornadas académicas que ofrece la Institución Universitaria Esumer en su sede de pregrados, su respectiva codificación o identificación y el horario. Fuente: Elaboración propia.
En cada una de las jornadas se ofrecen los diferentes programas académicos de pregrado, en el actual estudio solo se trabaja con la sede de pregrados, los posgrados de la Institución Universitaria Esumer se ofrecen en otra sede y no serán considerados en la aplicación del modelo. En la tabla 3 se muestra el detalle de los programas que se ofrecen, duración y la codificación que utilizaremos para simplificar el proceso de asignación.
Tabla 3: Programas académicos ofrecidos en la sede de pregrados.
# DE PROGRAMAS |
NOMBRE DEL PROGRAMA |
DURACION EN SEMESTRES |
CODIFICACION |
1 |
Tecnología en Comercio Internacional |
6 |
TCI |
2 |
Tecnología en Gestión Logística |
6 |
TGL |
3 |
Tecnología en Mercadeo |
6 |
TM |
4 |
Tecnología en Administración y Finanzas |
6 |
TAF |
5 |
Negocios Internacionales |
3 |
NI |
6 |
Administración Logística |
3 |
AL |
7 |
Nivelatorio de Administración Comercial y de Mercadeo |
1 |
NACM |
8 |
Administración Comercial y de Mercadeo |
3 |
ACM |
9 |
Administración Financiera |
3 |
AF |
En esta tabla se muestra el número de programas académicos que ofrece la Institución Universitaria Esumer en su sede de pregrados, su respectivo nombre o identificación, la duración en semestres y la codificación resumida. Fuente: Elaboración propia.
En nuestro caso particular y para efectos prácticos desarrollaremos el modelo aplicándolo a la jornada nocturna para realizar la asignación del segundo semestre del año 2015.
Se utilizó la siguiente codificación institucional para identificar los grupos:
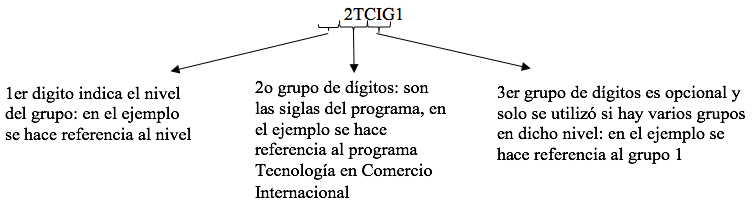
En la tabla 4 se muestra el detalle de los grupos que se planearon ofrecer en el segundo semestre del año 2015 en la jornada nocturna, la codificación que utiliza la Institución y la cantidad de alumnos esperada en cada grupo.
Tabla 4: Grupos a ofrecer y número de alumnos esperados para el segundo semestre del año 2015.
# DE GRUPO |
CODIFICACION INSTITUCIONAL |
# DE ALUMNOS |
1 |
1TCI |
30 |
2 |
2TCI |
30 |
3 |
3TCI |
30 |
4 |
4TCI |
30 |
5 |
5TCI |
30 |
6 |
6TCI |
40 |
7 |
7NIG1 |
25 |
8 |
7NIG2 |
25 |
9 |
8NIG1 |
25 |
10 |
8NIG2 |
25 |
11 |
9NI |
35 |
12 |
1TGL |
15 |
13 |
2TGL |
0 |
14 |
3TGL |
11 |
15 |
4TGL |
18 |
16 |
5TGL |
10 |
17 |
6TGL |
12 |
18 |
7AL |
30 |
19 |
1TM |
33 |
20 |
2TM |
33 |
21 |
3TM |
33 |
22 |
4TM |
33 |
23 |
5TM |
40 |
24 |
6TM |
40 |
25 |
NACM |
10 |
26 |
7ACMG1 |
15 |
27 |
7ACMG2 |
15 |
28 |
8ACMG1 |
15 |
29 |
8ACMG2 |
15 |
30 |
9ACM |
25 |
31 |
1TAF |
20 |
32 |
2TAF |
15 |
33 |
3TAF |
20 |
34 |
4TAF |
17 |
35 |
5TAF |
22 |
36 |
6TAF |
19 |
37 |
7AF |
25 |
38 |
8AF |
18 |
39 |
9AF |
24 |
40 |
1AE |
15 |
41 |
3AE |
6 |
En esta tabla se muestra el número grupos a ofrecer por la Institución Universitaria Esumer en su sede de pregrados durante el segundo semestre del año 2015, la codificación institucional y el número de alumnos que se esperan en cada grupo. Fuente: Elaboración propia.
A continuación, se describe el modelo de Programación Lineal a utilizar en forma particular aplicándolo a la jornada nocturna del segundo semestre de año 2015 de la Institución Universitaria Esumer.
Variables
m = cantidad de aulas disponibles (41 aulas)
n = cantidad de grupos a programar (41 grupos)
Ki = capacidad del aula i en términos de sillas disponibles. Ver Tabla 1 
Cj = cantidad de alumnos del grupo j. Ver Tabla 4
La variable 
está representada matemáticamente por la ecuación (1) y corresponde a una matriz de costos que contiene el número de sillas ociosas en una determinada asignación y si la capacidad del aula es menor al tamaño del grupo se asigna una penalización de 50, a continuación se muestra la figura 1 con la representación en una hoja de cálculo de esta variable.
Figura 1: Representación en una hoja de cálculo de la variable
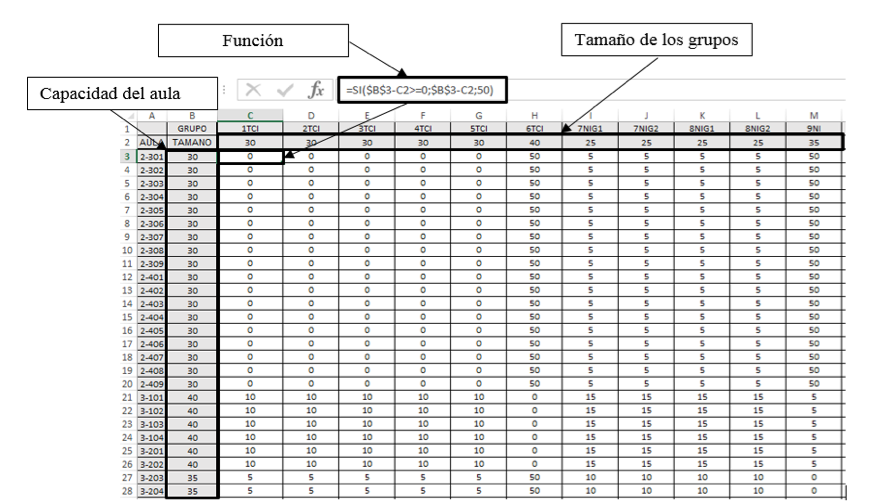
En esta figura se muestra la representación en una hoja de cálculo de la variable , la capacidad del aula y los tamaños de los grupos se expresan en sus respectivas filas y columnas. Fuente: Elaboración propia.
La variable de decisión 
está representada matemáticamente por la ecuación (2) y corresponde a una matriz de asignaciones que contiene ceros o unos en el lugar donde el modelo asigna a un grupo un aula, a continuación se muestra la figura 2 con la representación en una hoja de cálculo de esta variable.
Figura 2: Representación en una hoja de cálculo de la variable
En esta figura se muestra la representación en una hoja de cálculo de la variable 
. Fuente: Elaboración propia.
La restricción que garantiza que a todo grupo se le asigne un aula, está representada por la ecuación (3) y corresponde a la sumatoria de cada una de las columnas de la matriz que representa la variable y que fue explicada en la figura 2.
La restricción que garantiza que a toda aula se le asigne un grupo, está representada por la ecuación (4) y corresponde a la sumatoria de cada una de las filas de la matriz que representa la variable y que fue explicada en la figura 2.
La función objetivo que consiste en minimizar el número de sillas ociosas en la asignación total de la jornada nocturna y esto se representa con la ecuación (5) y corresponde a la suma producto de las matrices que representan las variables y
Finalmente se procede a utilizar el software RISKOptimizer de la Suit DecisionTools de Palisade, debido a que tenemos un modelo con 1681 variables representadas en la variable y 82 restricciones que corresponden a la asignación de 41 aulas y 41 grupos.
El RISKOptimizer genera un número de soluciones de prueba y utiliza algoritmos genéticos para mejorar constantemente los resultados de cada prueba. Para cada solución de prueba, se ejecuta una simulación Monte Carlo, muestreando funciones de distribución de probabilidad y generando un nuevo valor para la celda objetivo, una y otra vez. El resultado de cada solución de prueba es la estadística que desea minimizar o maximizar en la distribución de la celda objetivo. Se ejecuta otra simulación por cada nueva solución y se genera otro valor para la estadística objetivo.
La configuración del RISKOptimizer se puede apreciar en la siguiente figura.
Figura 3: Configuración del modelo en el software RISKOptimizer
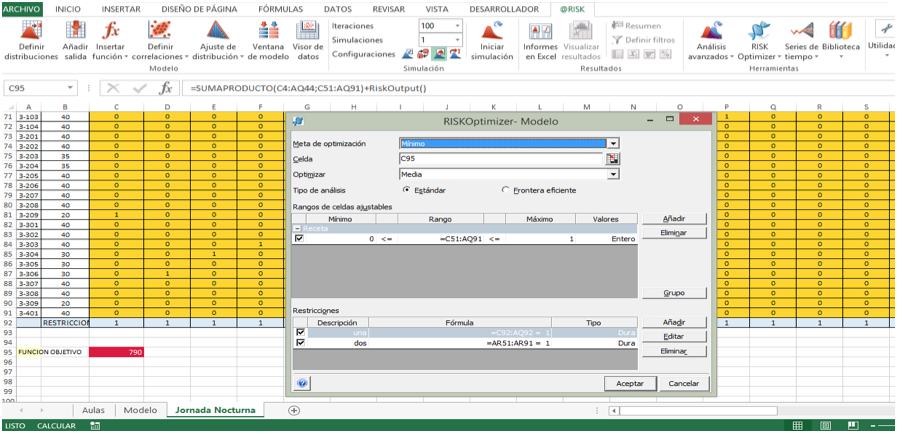
En esta figura se muestra la configuración del modelo en el software RISKOptimizer. Fuente: Ventana de configuración del modelo del software RISKOptimizer.
Para contrastar los resultados obtenidos en la asignación que arroja el modelo para el segundo semestre del año 2015, se toma como referente la asignación del primer semestre del año 2015, con el fin de comparar la mejora en la minimización de la función objetivo, recordemos que la función objetivo representa el número de sillas ociosas que quedan por semestre. Durante el primer semestre del año 2015 se tenía un costo de sillas ociosas en la asignación de 898 y al correr el modelo para el segundo semestre del año 2015 se obtiene un costo de 451 sillas ociosas, representando una disminución del 49.77% en el costo de asignación, obteniendo una mejora considerable en el proceso de asignación y garantizando que a grupos numerosos se le asigna un aula con gran capacidad y un grupo pequeño se le asigna un aula con baja capacidad.
En la siguiente tabla se observa el número total de pruebas del proceso de optimización, en nuestro caso son 1000 pruebas, con un tiempo total de optimización de 25 minutos con 44 segundos, un valor mínimo para la celda objetivo de 451, entre otros detalles.
Tabla 5: Resumen de las estadísticas del proceso de optimización.
Meta |
|
Celda a optimizar |
'Jornada Nocturna'!C95 |
Estadístico a optimizar |
Media |
Tipo de meta |
Mínimo |
Resultados |
|
Pruebas válidas |
1000 |
Total de pruebas |
1000 |
Valor original |
790 |
+ penalizaciones de restricciones blandas |
0,00 |
= resultado |
790 |
Mejor valor encontrado |
451 |
+ penalizaciones de restricciones blandas |
0,00 |
= resultado |
451 |
Número de la mejor prueba |
113 |
Tiempo para encontrar mejor valor |
0:05:49 |
Razón de detención de optimización |
Número de pruebas |
Tiempo de inicio de optimización |
28/05/2015 11:27 |
Tiempo de fin de optimización |
28/05/2015 11:54 |
Tiempo total de optimización |
0:25:44 |
En esta tabla se muestra el número de pruebas que se realizaron durante el proceso de optimización, el mejor valor encontrado para la celda objetivo que en nuestro caso es de 451, el número de la mejor prueba, el tiempo total de optimización, entre otros detalles. Fuente: Informe de optimización del software RISKOptimizer.
Las pruebas en las cuales se obtiene una mejora en el proceso de optimización se observan en la siguiente imagen, básicamente son en las pruebas 1, 2, 26, 61, 87, 105 y 113, podemos observar que en los primeros 5 minutos y 49 segundos se optimizó el modelo a pesar de que el proceso total demoró 25 minutos y 44 segundos.
Figura 4: Informe de Registro de Pasos de Progreso del software RISKOptimizer
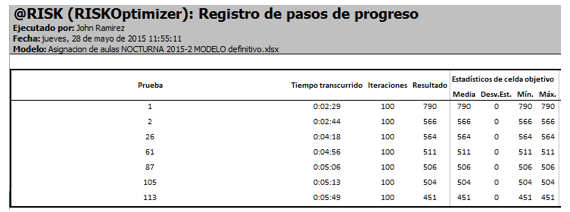
En esta figura se muestra la el registro de pasos durante el proceso de optimización.
Fuente: Informe del software RISKOptimizer.
En forma gráfica podemos observar la evolución del proceso de optimización en la siguiente figura, obsérvese que en las primeras 200 pruebas ya se había llegado a la solución óptima.
Figura 5: Informe gráfico de Registro de Pasos de Progreso del software RISKOptimizer
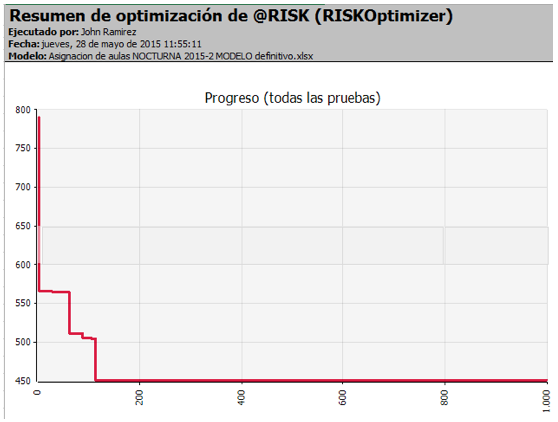
En esta figura se muestra la el registro de pasos y la evolución del proceso de optimización en forma gráfica.
Fuente: Informe del software RISKOptimizer.
La información obtenida de los resultados permite optimizar la asignación de los salones y reducir los costos asociados a los mismos, pues al contrastar la asignación de aulas para el segundo semestre académico del año 2015 arrojada por el modelo, con la asignación manual que se utilizó en el primer semestre académico del año 2015, se redujeron las sillas ociosas en un 49.77%.
El modelo para la asignación de aulas planteado en este artículo y cuyo componente lógico se basa en la programación lineal, ha sido implementado en un ambiente de pruebas y utilizando datos reales suministrados por el área de gestión de recursos académicos de la Institución Universitaria Esumer. Este modelo ha presentado un mejor desempeño comparado con el método manual que actualmente aplica la universidad; este efecto ha permitido la optimización de los recursos académicos, la disminución de los costos de algunos de sus programas ofertados y el bienestar de los estudiantes al tener espacios mejor pensados dependiendo del número de alumnos que tiene cada grupo.
Crovo, A. S., San Martín, C. O., & Rojas, L. P. (2007). Modelos de programación entera para un problema de horarios para universidades. Ingeniare. Revista chilena de ingeniería, 15(3), 245-259.
Dammak A., Elloumi A. y Kamoun H. (2007). An enterprise system component based on graph colouring for exam timetabling. A case study in a Tunisian university. Transforming government: people, process and policy, 1(3), 255 – 270.
Daskalaki S., Birbas T. y Housos E. (2004). An integer programming formulation for a case study in university timetabling. European Journal of Operational Research, 153(1), 117 – 135.
Hernández R., Miranda J. y Rey P. (2008). Programación de horarios de clases y asignación de salas para la Facultad de Ingeniería de la Universidad Diego Portales mediante un enfoque de programación entera.
Revista Ingeniería de sistemas, XXII, 121 – 141.
Saldaña A., Oliva C. y Pradenas L. (2007). Modelos de programación entera para un problema de programación de horarios para universidades. Ingeniare, Revista chilena de ingeniería, 15 (3), 245 – 259.
Shiau D. (2011). A hybrid particle swarm optimization for a university course scheduling problem with flexible preferences. Expert Systems with Applications: An International Journal, 38(1), 235 – 248.
Soria‐Alcaraz J.A., Carpio‐Valadez J. y Terashima‐Marin H. (2011). Academic Timetabling Design Using Hyper‐Heuristics. Studies in Computational Intelligence, 318, 43‐ 56.
Yakoob S., Sheraly H. (2007). A mixed‐integer programming approach to a class timetabling problem: A case study with gender policies and traffic considerations. European Journal of Operational Research, 180(3), 1028 – 1044.
1. Magister en Ingeniería administrativa, Universidad Nacional de Colombia sede Medellín. Profesor tiempo completo. Institución Universitaria Esumer. E-mail: eduardo.duque@esumer.edu.co
2. Magíster en Gestión Financiera Universidad Complutense de Madrid. Profesor tiempo completo. Institución Universitaria Esumer. E-mail: jdgonzalez@esumer.edu.co
3. Ingeniero Industrial y Magister en Ingeniería de la Universidad de Antioquia, Medellín, Colombia. Coordinador del Programa académico Administración Financiera de la Institución Universitaria Esumer. E-mail: john.ramirez99@Esumer.edu.co