ISSN 0798 1015

Vol. 38 (Nº 04) Año 2017. Pág. 20

Container crane controller with the use of a NeuroFuzzy Network

Controlador de ponte rolante de contêiner com uso de uma Rede NeuroFuzzy

Ricardo Pinto FERREIRA 1; Andréa MARTINIANO 2; Arthur FERREIRA 3; Marcio ROMERO 4; Renato José SASSI 5

Recibido: 15/08/16 • Aprobado: 06/09/2016

Content

1. Introduction

2. Theoretical Bases

3. Materials and Methods

4. Results of Computational Experiments

5. Conclusions

References

1. Introduction

The container crane are widely used to transfer heavy loads in ports and shipyards. This transfer is desirable that the container crane transport the loads to the desired position as quickly and as accurately as possible without colliding with any other equipment.

This rapid movement naturally induces undesirable balance of the container, which could cause damage to the load and other types of hazards, also reducing the performance of the operation. Therefore, these oscillations in the track must be damped before another container come into operation.

Thus, the performance transshipment loses the desired efficiency, increasing the cost involved in the operation and the risk of accidents with heavy loads that are transferred continuously throughout the operation.

Fuzzy Logic was developed in 1965 with the work of Zadeh (1965) to represent the uncertain, imprecise and vague knowledge. Fuzzy Logic translates the ambiguous information, imprecise, uncertain, in numeric values and include the human experience in intelligent systems, processed by computer, and versatile for solving real problems.

The Fuzzy Logic concepts were born inspired by traditional logic, although changes have become necessary to adapt them to the requirements of engineering applications (PACHECO & VELLASCO, 2007).

The use of Fuzzy Logic has been growing in several areas of knowledge, as in the control of electromechanical systems, character recognition, robotics, elevator systems, landing aircraft, etc. The growth in the use of fuzzy logic is due to its great simplicity of implementation, and require little tired in its modeling, which provides both for the manufacturer, which reduces their costs, and the final consumer who acquires a more efficient product (COSTA, 2010).

Artificial Neural Networks (ANNs) are a from the Artificial Intelligence technique based on simulation of the functioning of the brain by computer data structures, the great motivation of the use of this technique in performing tasks that require fault tolerance, flexibility, imprecision and parallelism (HAYKIN, 2001).

The NeuroFuzzy Network (NFN) ANNs are applied in various fields such as modeling, time series analysis, pattern recognition, signal processing, control, image recognition and data mining (KAYKIN, 2001; BIGUS, 1996; MAASS & BISHOP, 2001; SILVA, SPATTI & FLAUZINO, 2010; BRAGA, CARVALHO & LUDEMIR, 2011; GOLDSCHMIDT, PASSOS & BEZERRA, 2015; FERREIRA et al., 2016).

The NFN is the combination of Fuzzy Logic and ANNs, some techniques may be combined to generate the so-called hybrid systems, or hybrid architectures. The advantage of this type of system must be obtained by cooperation combination of techniques (SASSI, 2012).

In this context, the NFN is an alternative to the development of new studies seeking the possible applications of these techniques in engineering problems. Several studies have been published to control the cranes containers, describes some recent work related to this study that arouse interest, fuzzy logic to control cranes (COSTA, 2010; MOHAMMED, HAYAJNEH, RADAIDEH & SMADI, 2006; CHANG, 2007; YU, ARMENDARIZ & RODRIGUEZ, 2011; ZHAO & GAO, 2012; SMOCZEK & SZPYTKO, 2014; QIAN, TONG & LEE, 2016). cranes controller using fuzzy clustering techniques Sadati & hooshmand (2016), parallel neural network for crane control Lee, Huang, shih, Chiang & Chang (2014), adaptive control crane (NGUYEN, NGO & KLIN, 2015). The motivation for the development of research is the joint use of the techniques.

The aim of the paper was to present a container crane controller pre-project using a NFN. The paper is organized after this introductory section as follows: Section 2 presents the Theoretical Bases: the basic concepts of Fuzzy Logic, ANNs, NFN and container crane, in Section 3 presents the materials and methods. Are described in section 4 the results of computational experiments. Section 5 conclusions.

2. Theoretical Bases

2.1. Container Crane

Figure 1 illustrates a crane container with its basic elements: the cart, (responsible for the displacement), the opening angle (), the load (container), cable (support), the track and the direction of the force gravity.

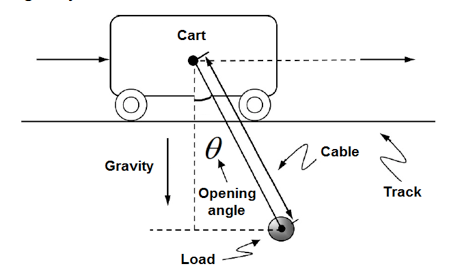
Figure 1. Container crane. Source: Adapted from Qian, Tong & Lee (2016), Smoczek (2014), Peng-Cheng, Yong-Chun & Zi-Ya (2014).

2.1. Fuzzy logic

Fuzzy logic is a mathematical theory, which aims to model human reasoning, mimicking the human ability to make decisions in uncertain and imprecise environments, expressed by a set of linguistic variables (PACHECO & VELLASCO, 2007; GOLDSCHMIDT, PASSOS & BEZERRA, 2015).

It uses the concept of fuzzy logic as the mathematical tools necessary for the treatment of logic and algebraic operations in the universe of fuzzy sets (PASSINO & YURKOVICH, 1998).

In this case, we used the nomenclature of fuzzy sets defining them as a class of continuous variables objects. Those sets are characterized by membership functions, which indicate for each element a degree of relevance 0-1 (NICOLETTI & CAMARGO, 2004).

In classical set theory, the relevance of an element to a set is well-defined. Nevertheless, for a wide range of physical phenomena it is difficult to clearly establish whether an element belongs or not a particular set. Thus, Zadhe (1965) proposed a broader characterization, such that membership function may assume continuous values between 0 (zero) and 1 (one).

The concepts of intersection, union, complement, convexity, etc., are extended to those sets and various properties of these notions in the context of fuzzy sets are established in the work of (ZADHE, 1965).

The membership functions have various forms, depending on the concept you want to express and can be set from the user's needs, but it is common to use standard membership functions, such as: triangular function, trapezoidal and Gaussian, or even, through analytics (REZENDE, 2005).

The central question for consistency to model a system by Fuzzy Logic is the determination of a rule base representing the satisfaction of its dynamics, that is, as the input variables are related to each other, what there are outputs and, from that, their corresponding associated errors are determined. Therefore, the accuracy of the model is directly proportional to the adhesion between the real dynamics of the system and the basic proposal rules to represent it (ZADHE, 1965).

Related systems some features where the application of fuzzy logic is necessary or beneficial. Such complex systems are difficult to model, as an example we can mention: systems controlled by human experts, systems with inputs and complex and continuous outputs, systems which use the human observation, as starters or as the basis for rules, systems that are naturally inaccurate as the description systems is extremely complex (McNEILL & THRO, 1994).

According to Russel (2007), for a particular element should be established whether this belongs to a class. However, in the real world people use this concept in a very vague way. Therefore, for a wide range of physical phenomena it becomes difficult to clearly establish whether or not an element belongs to a given class.

The application of fuzzy logic for predicting or monitoring, for a given system is characterized by use of an inference engine. By this mechanism comprises the set of rules that applied correctly to the field of objects, is the system dynamic objects to which they belong. This feature makes it necessary that the events displayed in the entry must necessarily be classified in one of these rules (SIMÕES & SHAW, 2007).

  According to Carvalho (2008), the establishment of the inference engine that simulates a system involves two stages: the premises of all the rules are compared to the controlled inputs to determine which rules apply in a given situation, then the conclusions are established using the rules which have been determined.

To represent the inference mechanisms in fuzzy sets, we used the concept of fuzzy relationship, which generalizes the concept of present relations in the Classic Set Theory and represent the degree of association between elements of two or more fuzzy sets (CARVALHO, 2008).

2.2   Artificial Neural Networks

The ANNs are models inspired in brain structure aiming to simulate human behavior in processes such as learning, adaptation, association, fault tolerance, generalization and abstraction (HAYKIN, 2001; SILVA, SPATTI & FLAUZINO, 2010; SIMÕES & SHAW, 2007; TKÁC & VERNER, 2016).

In the ANNs learning occurs through a set of simple processing units called artificial neurons. In Figure 2 is shown a representation of the artificial neuron. the data is observed (data vectors) neuron input (X₁, ..., X_n), the neurons of the input layer (W_1J ..., W_nj) with their respective weights, then immediately the additive junction or sum represented by the letter sigma, then the activation function (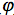) and finally the output (y).

Figure 2. Representation of the artificial neuron. Source: Adapted from Haykin (2001).

In a conventional computer system, if a failure part, in general the system as a whole deteriorates, while in an ANN, the fault tolerance is a part of architecture, due to its distributed nature processing. If a neuron fails, your erroneous output is overwritten by the correct output of its neighboring elements. So, at first, an ANN exhibits a soft performance degradation instead of presenting a catastrophic failure (HAYKIN, 2001).

One of the first ANNs, whose architecture is based on the biological neuron, has been proposed by Rosenblatt (1959) the Perceptron. The purpose of this network is to classify the inputs xi (or stimulus) into two classes by a hyperplane. For the simple case of a space in two dimensions, the hyperplane is reduced to a straight line whose equation is represented in (1).

The activation is performed through artificial neuron activation function, which performs j similar to the biological neuron synapse task, transmitting or blocking nerve impulses.

In general, learning Perceptron networks is through the adjustment of synaptic weights. The value of the synaptic weight W ^(t+1) at the instant _t+1, its will be determined on the basis of its value in the previous iteration wt, according to Equation (2).

The updating of the weights depends on the algorithm, but generally is based on minimizing the error E_i, between the values proposed by the network and outputs y_i desired, as Equation (3).

Thus, the learning (or training) on an ANN is defined as the iterative adjustment of synaptic weights to minimize errors (KAYKIN, 2001). A general definition of what constitutes learning in an ANN can be expressed as follows: "Learning is the process by which the parameters of an ANN are adjusted through a continued form of stimulus by the environment in which the network is operating, and the specific type of learning accomplished defined by particular way to the setting of the parameters occur " (MENDEL & MCLAREN, 1970).

Several methods for learning have been developed and can be grouped into two main paradigms: supervised learning and unsupervised learning.

In supervised learning, there is a prior knowledge of the values of x_i y_i inputs and their outputs. In this set of ordered pairs (x_i, y_i), that is known a priori gives the learning database name. The most widely used algorithm is the retro error propagation (error back-propagation) used by the MLP type ANN used in this work.

A Multilayer Perceptrons is one of the most used ANN in classification. The ANN architecture MLP typically consist of a specification of the number of layers, type of activation function of each unit and weights of connections between the different units should be established for the construction of the neural architecture (KAYKIN, 2001).

The error back-propagation training algorithm works as follows: shows a pattern in input layer of the network, this pattern is processed, layer by layer, until the output provides the processed response, f_MLP, calculated as shown below in Equation (4). where v_l and wlj are synaptic weights; b_l0 and b₀ are biases; and φ the activation function.

Learning an ANN, in most cases, it happens to a subset of examples (data vectors) which define the so-called training set and ANN testing is performed with another subset of examples (data vectors) which define the so-called test set.

The ANNs can be trained using random initial values for the weights of connections. The learning parameters are initialized and data vectors training patterns are presented to the ANN. Throughout the training progress the connections weights are adjusted and you can monitor the performance of ANN (KAYKIN, 2001).

2.3   Neuro Fuzzy Network

According to Goldschmidt & Passos (2015), some techniques can be combined to generate the so-called hybrid or hybrid architectures systems. The advantage of this type of system is due to the synergy obtained by combining two or more techniques. This synergism reflects in getting a more powerful system (in terms of interpretation, learning, estimation parameters, training, among others) and with fewer disabilities.

 A very interesting combination and it generally gives good results is to associate an ANN with Fuzzy Logic (PACHECO & VELLASCO, 2007; SASSI, 2012). The purpose of this combination is to get good ability to learn and adapt to the needs to solve real-world problems, ideal for applications such as identification, prediction, classification and control (PACHECO & VELLASCO, 2007;  SIMÕES & SHAW, 2007).

  According Nauck, Klawonn & Kruse (1996), NFN is the term used for approaches that have the following properties:

  - They are based on Fuzzy Logic and are trained by a learning algorithm derived from one of ANNs. The learning procedure (heuristic) operates in local information, and causes only local changes in the foundation of NFN;

  - Have three layers where the first layer is the input variables, the middle layer (hidden) represents the inference rules and the third layer is the output variables;

  - Can always be interpreted as an inference engine. Since not all learning templates specify procedures for creation of fuzzy rules;

  - The learning procedure of NFN transforms the semantic properties of a fuzzy system into a set of descriptions. This results in restrictions that may become relevant changes to system parameters, however, not all approaches in a NFN possess this property;

  - Near an n-dimensional function that is defined in part by training data.

 In this section we were addressed the basics of artificial neural network, fuzzy logic and fuzzy neuro network.

3. Materials and Methods

Was used in this work an ANN Multilayer Perceptron (MLP) combined with fuzzy logic forming a NFN. The MATLAB software was used to generate the 15 fuzzy rules, the inference model and the response surface. The hardware platform used in the experiments was a computer with Intel® Core ™ 2 Duo CPU T6600 2.20 GHz with 4.00 GB of memory, 1 TB hard drive

To model the fuzzy membership functions of the speed of moving container bridge we used three Gaussian functions: low, medium and high. To model the fuzzy membership functions with the angle of the crane container were used five Gaussian functions: large negative angle, small negative angle, angle zero, small positive angle and large positive angle. The tractive power was modeled in three functions of Gaussian relevance: low, medium and high [1].

The parameters used in ANN were: number of input neurons equal to 2 (the fuzzy inference to: speed and angle), the number of layers equal to 2, the number of neurons in the hidden layer equal to 10, the initial rate of learning equal to 0, 3 with decay 1% every 20 times, starting time factor of 0.3 to decay 1% every 25 times, stopping criterion was the maximum number of times equal to 150. the ANN training was sequential (online), and the processing time was 5 seconds. The output of the NFN was the tractive power.

Figure 3 illustrates the hybrid topology of NFN used in the experiment.

Figure 3. Hybrid topology NeuroFuzzy used in the experiment.

4. Results of Computational Experiments

Figure 4 illustrates the fuzzy membership functions generated by the 15 rules (Speed, Angle and power).

---

Figure 4. Fuzzy pertinence functions.

 ---

Figure 5 illustrates the response surface modeled by the 15 fuzzy rules (left side: angle, right side: speed).

Figure 5. Response surface area modeled by the 15 fuzzy rules.

---

Figure 6 shows the validation phase of NFN.

Figure 6. Validation phase NFN.

It notes that the results presented in the validation phase of NFN was quite satisfactory for the proposed issue, which reinforces the use of NFN in this type of control application.

5. Conclusions

With the initial result is noted that the response surface 15 obtained through the fuzzy rules, allows pre-design a control mechanism, including the inputs and outputs required development system container crane controller.

The NFN presented adherent experimental results, the use of fuzzy logic associated with the ANN produced an inference engine capable of representing the dynamics of a crane container. Thus, the results indicate positively to the implementation of the proposed NFN control problem. It contributes to the formulation of simple programming controllers.

For future studies we intend to refine the fuzzy membership functions in order to improve the performance of NFN. The aim is also to test other artificial neural networks with other topologies and parameters. It aims also to future studies pre-design a fuzzy neural control mechanism for three-dimensional container crane.

References

Bigus, J. P. (1996). Data Mining with Neural Network: Solving Business Problems from Applications Development to Decision Support. McGraw-Hill.

Braga, A. P., Carvalho, A. C. P. L. F., Ludermir, T. B. (2011). Redes Neurais Artificiais: Teoria e Aplicações. 2ª ed. Rio de Janeiro: LTC.

Carvalho, L. M. F. (2008). A neuro-fuzzy system to support in the diagnostic of epileptic events using different fuzzy arithmetical operations. Neuropsiquiatria, p.179-183.

Chang, C. Y. (2007). Adaptive fuzzy controller of the overhead crane with nonlinear disturbances. IEEE Transactions on Industrial Informatics. v.3 (2),164–172.

Costa, H. C. (2010). Aplicação de técnicas de modelagem e controle em sistemas tipo ponte rolante. Dissertação de Mestrado, Instituto Militar de Engenharia, Rio de Janeiro.

Ferreira, R. P., Martiniano, A., Ferreira, A., Ferreira, A.; Sassi, R. J. (2016). Study on daily demand forecasting orders using artificial neural network. IEEE Latin America Transactions, v.14, n. 3, p.1519-1525.

Goldschmidt, R., Passos, E., Bezerra, E. (2015). Data mining: Conceitos, técnicas, algoritmos, orientações e aplicações, Rio de Janeiro, 2 eds. Elsevier.

Haykin, S. (2001). Redes Neurais – Princípios e Práticas. 2ª edição. Porto Alegre: Bookman.

Lee, L. H., Huang, P. H., Shih, Y. C., Chiang, T., Chang, C. (2014). Parallel neural network combined with sliding mode control in overhead crane control system, Journal Vib. Control, v.l20 (5), p.749–760.

Maass, W., Bishop, C. M. (2001). Pulsed Neural Networks. Cambridge: First MIT Press paperback edition.

McNeill, F. M.; THRO, E. (1994). Fuzzy Logic: A practical approach. AP Professional/Academic Press.

Mendel, J. M., Mclaren, R. W. (1970). Reinforcement-learning control and pattern recognition systems. Adaptive, Learning and Pattern Recognition Systems. Academic Press, New York e London, Cap. 8, p. 287–318.

Mohammed, T., Hayajneh S. M., Radaideh, I., Smadi, A. (2006). Fuzzy logic controller for overhead cranes. Engineering Computations, Vol. 23 Iss.1 p. 84 – 98.

Nauck, D., Klawonn, F., Kruse, R. (1996). Foundations of Neuro Fuzzy Systems. Willey & Sons.

Nguyen, Q. C., Ngo, H. Q. T., klin, W. H. (2015). Nonlinear adaptive control of a 3D overhead crane. Control, Automation and Systems (ICCAS), 15th International Conference, Busan, Korea. p.41-47.  

Pacheco, M. A. C., Vellasco, M. M. B. R. (org). (2007). Sistemas inteligentes de apoio à decisão: análise econômica de projetos de desenvolvimento de campos de petróleo sob incerteza. Rio de Janeiro: Ed. PUC-Rio: Ed. Interciência. Passino, K. M., Yurkovich, S. (1998). Fuzzy Control, Addison Wesley Longman, Inc.

Peng-Cheng, W., Yong-Chun, F., Zi-Ya, J. (2014). A Direct Swing Constraint-based Trajectory Planning   Method for Underactuated Overhead Cranes. Acta Automatica Sinica, v.40 (11), p. 2414-2419.

Qian, D., Tong, S., Lee, S. (2016).  Fuzzy-Logic-based control of payloads subjected to double pendulum motion in overhead cranes. Journal Automation in Construction. v.65, p. 133–143.

Rezende, S. O. (2005). Sistemas Inteligentes: Fundamentos e Aplicações. Barueri: Manole.

Rosenblatt, M. (1959). The Perceptron: A probabilistic model for information storage and organization in the Brain. Psychological review, v.65, n.6, p. 386-408.

 Russel, B. (2007). Introdução a Filosofia matemática; tradução Maria L. X. A. Borges, Ed Jorge Zahar, Rio de Janeiro.

Sadati, N., Hooshmand, A. (2016). Design of again-scheduling anti-sway controller or tower cranes using fuzzy clustering techniques. In: Proceedings of the International Conference on Computational Intelligence for Modeling, Control and Automation, Sydney, Australia.

Sassi, R. J. (2012). An hybrid architecture for clusters analysis: rough setstheory and self organizing map artificial neural network. Pesqui. Oper. Rio de Janeiro, v. 32, n. 1, p. 139-164.

Silva, I. N., Spatti, D. H., Flauzino, R. A. (2010). Redes Neurais Artificiais para Engenharia e Ciências Aplicadas. SP: Artliber.

Simões, M. G., Shaw, I. S. (2007). Controle e Modelagem fuzzy. São Paulo: Blucher: FAPESP.

Smoczek, J. (2014). Fuzzy crane control with sensor less payload deflection feedback for vibration reduction. Journal Mechanical Systems and Signal Processing. v.46, p.70–81.

Smoczek, J., Szpytko, J. (2014). Evolutionary algorithm-based design of a fuzzy TBF predictive model and TSK fuzzy anti-sway crane control system. Journal Engineering Applications of Artificial Intelligence. v.28, p.190–200.

Tkác, M., Verner, R. (2016). Artificial neural networks in business: Two decades of research. Journal Applied Soft Computing. v. 38. p.788–804.

Yu, W.; Moreno-Armendariz, M. A., Rodriguez, F. O. (2011). Stable adaptive compensation with fuzzy CMAC for an overhead crane. Information Sciences. v.181, p.4895–4907.

Zadeh, L. A. (1965).  Fuzzy Sets, Information and Control, v.8. p. 338-353.

Zhao, Y., Gao, H. J. (2012). Fuzzy-model-based control of an overhead crane with input delay and actuator saturation, IEEE Trans. Fuzzy Syst. v.20, p.181–186.

1. Doutorando em Informática e Gestão do Conhecimento – Universidade Nove de Julho. E-mail: kasparov@uni9.pro.br

2. Mestre em Engenharia de Produção – Universidade Nove de Julho. E-mail: andrea.martiniano@gmail.com

3. Graduando em Sistema de Informação – Universidade de São Paulo. E-mail: arthur2.ferreira@usp.br

4. Mestre em Engenharia de Produção – Universidade Nove de Julho. E-mail: mhromero@hotmail.com

5. Doutor em Engenharia Elétrica - Universidade Nove de Julho. rjsassi@gmail.com