HOME | ÍNDICE POR TÍTULO | NORMAS PUBLICACIÓN

Espacios. Vol. 37 (Nº 38) Año 2016. Pág. 14

Previsão do preço do trigo para indústria moageira do Rio Grande do Sul

Prediction of the price of wheat for milling industry of Rio Grande do Sul

Alessandro Xarão da COSTA 1; Adriano Mendonça SOUZA 2

Recibido: 14/07/16 • Aprobado: 10/08/2016

Conteúdo

1. Introdução

2. Fundamentação teórica

3. Aspectos metodológicos

4. Análise dos dados e previsão

5. Conclusão

Referências

1. Introdução

O trigo é um dos ingredientes básico utilizado na alimentação humana. No processo de produção as indústrias moageiras separam as partes do grão, a parte externa chamada de casca vai constituir o farelo de trigo destinado à alimentação animal e a parte interna do grão as farinhas utilizadas na fabricação de pães, massas, biscoitos e outros (EMBRAPA, 2016). A moagem nacional de trigo em 2015 foi de 10,421 milhões de toneladas, sendo 42,1% consumida pela Região Sul do Brasil e 13,91% pelo estado do Rio Grande do Sul (ABITRIGO, 2016). Por se tratar de uma commodities suas flutuações de preços diários são baseados na oferta e na procura global pelo produto.

Através da análise dos dados estatísticos de importação e consumo de trigo no Brasil disponibilizados pela Associação Brasileira da Indústria do Trigo, verifica-se que o país não é autossuficiente na produção do grão, necessitando importar nos últimos quatro anos cerca de 56% do trigo necessário para a indústria moageira.

No primeiro semestre de 2015 os preços do cereal aumentaram em até 20% devido a disputa do grão entre moinhos e fábricas de rações que demandaram de trigo para substituir o milho, cujos preços subiram ainda mais (ABITRGO, 2016).

A indústria moageira trabalha com preços de farinha excessivamente competitivos entre si, tendo como característica deste mercado a facilidade de informações a respeito do preço do concorrente. O preço é norteado pelo mercado e influenciado por algumas empresas dominantes, contudo quando bem administrado conduz a empresa, a maximização do lucro (LIMA, 2005).

Diante de um mercado competitivo onde as indústrias moageiras estão inseridas e sendo o trigo a principal matéria-prima da farinha representando cerca de 70% do custo de seu faturamento líquido, a informação sobre os custos futuros do trigo torna-se um dado de suma importância na gestão dos custos produtivos e estoques de trigo das indústrias moageiras.

O objetivo desta pesquisa é realizar uma previsão para o preço do trigo no Rio Grande do Sul a partir de uma série temporal que compreende o período de Julho de 2006 a Junho de 2016, consultadas no Centro de Estudos Avançados em Economia Aplicada (CEPEA- ESALQ/USP).

2. Fundamentação teórica

Nesta seção serão denotadas as explicações de séries temporais e os modelos de Box & Jenkins, subseção está que apresenta as etapas necessárias para a metodologia e os critérios de seleção penalizadores que serão utilizados, imprescindíveis para a previsão do preço do trigo no Estado do Rio Grande do Sul.

2.1 Séries Temporais

Uma série temporal tem como característica ser um conjunto de dados de uma determinada variável observado sequencialmente ao longo do tempo, apresentando uma dependência seriada e geralmente com distâncias equidistantes e preocupa-se em estudar esta relação de dependência entre as observações (BOX; JENKINS; REINSELL, 2008)

A previsão de uma série temporal é uma estimativa quantitativa a cerca da verossimilhança de eventos futuros dos valores da série, desta forma, são extrapolações geradas através das funções de previsão ou equações de previsão, para um período superior ao do modelo estimado (BOX; JENKINS; REINSELL, 2008). As previsões ex-post são realizadas para gerar valores dentro do próprio período com a intenção de verificação do modelo e, previsões ex-ante aquelas geradas antes do acontecimento dos fatos.

O modelo Box-Jenkins (BJ) leva este nome em homenagem a George Box e Gwilym Jenkins que nos anos de 1970 utilizando uma abordagem matemática criaram o modelo com a  intenção de descrever as mudanças na série temporal. Conhecido tecnicamente como modelo ARIMA, trás a ênfase em analisar as propriedades estocásticas de séries temporais econômicas observando o passado da própria série para fins de previsões, ou seja, “deixar que os dados falem por si mesmos” (GUJARATI, 2000; GREENE, 2003).

O método modela a função de autocorrelação de uma série estacionária, seu modelo geral é o autorregressivo integrado de médias móveis- ARIMA (p, d, q), sendo p o número de termos autorregressivos, d o número de diferenciações necessárias para a estacionariedade da série e q a ordem máxima de parâmetros de médias móveis, para (p, d, q >=0). AR (p) é a parcela autorregressiva que modela a dependência de um valor atual sobre valores passados, MA (q) a parcela de média móvel que considera que os valores atuais são dependentes de erros de previsão de períodos passados (ruídos brancos) (GUJARATI, 2000; SOUZA e MARCHEZAN, 2010). Conforme Box, Jenkins e Reinsell (2008) a equação geral do modelo não sazonal é dada por:

Os modelos SARIMA (p, d, q)(P, D, Q)s, são utilizados quando existe a presença de sazonalidade na série temporal, p e q representam, respectivamente, às ordens autorregressiva e de média móvel; P refere-se a ordem autorregressiva sazonal e Q a ordem de média móvel sazonal (SOUZA, F. et al., 2010). Para Box, Jenkins e Reinsell (2008) a equação geral do modelo sazonal é dada por:

A metodologia Box-Jenkins pode ser desenvolvida em 4 etapas: identificação, estimativa, checagem de diagnóstico e previsão (GUJARATI,  2000; GREENE, 2003).

Etapa 1. Identificação

Consiste em determinar os valores apropriados para os filtros AR (p), I (d), MA (q) do modelo ARIMA utilizando como uma ferramenta padrão a análise da função de autocorrelação (FAC) e função de autocorrelação parcial (FACP). Em geral, os modelos devem ser parcimoniosos, o que significa conter um número pequeno de parâmetros.

A função de autocorrelação possibilita identificar o quanto a informação do período  está relacionada com a observação anterior , além da sazonalidade, ciclos e demais padrões da série.

A função de autocorrelação parcial é utilizada para medir o grau de correlação entre as observações da série temporal,  e  depois de eliminado o efeito dos y’s intermediários, ou seja, permite avaliar o grau de correlação da variável atual com seus valores anteriores enquanto mantêm-se os demais valores constantes (MAKRIDAKIS; WEEL WRIGHT; HYNDMAN, 1998; GUJARATI, 2000; ALBUQUERQUE; MORAES, 2007).

Segundo Greene (2003) a função de autocorrelação (FAC), é definida por:

A função de autocorrelação parcial (FACP) é definida por:

Etapa 2. Estimação

Depois da identificação dos melhores valores para p e q na etapa anterior, é necessário estimar os parâmetros dos termos autorregressivos e de médias móveis. Aqui deseja-se encontrar um modelo com erro característico de “ruído branco”, isto é, com média zero, variância constante e não-autocorrelacionados, condição necessária para ser independente e identicamente distribuído (i.i.d.) (MONTGOMERY; JENNINGS; KULAHCI, 2008; SOUZA, F. et al., 2010).

Outra condição avaliada no modelo é o da parcimônia, está procura o equilíbrio entre a inclusão de defasagens adicionais no modelo e a redução da soma dos quadrados dos erros estimados. Um dos critérios de seleção de modelos mais utilizados para este trade-off são o Akaike Information Criterion (AIC) e o Schwartz Bayesian Criterion (SBC) (ALBUQUERQUE; MORAIS, 2007). O modelo selecionado será o que apresentar o menor AIC e BIC (SOUZA, F. et al., 2010).

Segundo Albuquerque e Morais (2007) as fórmulas dos critérios AIC e BIC são as seguintes:

AIC= T In (soma do quadrado dos resíduos) + 2n

BIC= T In (soma do quadrado dos resíduos) + n In(T)

Sendo:

n= número de parâmetros estimados;

T=número de observações utilizadas.

Etapa 3. Checagem

Nesta etapa verifica-se a existência de autocorrelação serial dos resíduos, uma das análises desta existência ou não, é dada pela função de autocorrelação (FAC) e função de autocorrelação parcial (FACP) dos resíduos e seus respectivos correlogramas. Analisando a FAC e FACP dos resíduos deseja-se que para erros aleatórios nenhum coeficiente de autocorrelação ou autocorrelação parcial seja significativo (MAKRIDAKIS; WEEL WRIGHT; HYNDMAN, 199).

Etapa 4. Previsão

A popularidade da modelagem ARIMA deve-se ao seu sucesso em fazer previsões, especialmente dentro de um período de curto prazo, em muitos casos não ultrapassando 12 passos à frente. Para obtenção das previsões, após a determinação do modelo, o método identifica as correlações históricas entre os dados e as generaliza para períodos futuros (MAKRIDAKIS; WEEL WRIGHT; HYNDMAN, 1998). A previsão ex-ante é realizada para calcular valores futuros, em um curto prazo, da variável em estudo, enquanto a previsão ex-post é feita para gerar valores dentro do período amostral.

Através do erro quadrático médio (EQM) o qual é determinado somando os erros de previsão ao quadrado e dividindo pelo número de erros usados no cálculo, será possível verificar a eficiência do modelo estimado. Quanto menor o erro quadrático médio, maior qualidade é atribuída as previsões do modelo previsto. Segundo Lemos (2006), o EQM é denotado por:

3. Aspectos metodológicos

Esta pesquisa tem como objetivou prever os preços do trigo para o segundo semestre de 2016 no Estado do Rio Grande do Sul por meio dos modelos ARIMA (Auto Regressive Integrated Moving Average), a previsão constitui um meio de fornecer informações e subsídios para tomada de decisão. Para o desenvolvimento desta pesquisa foram utilizados os modelos ARIMA (Auto Regressive Integrated Moving Average).

As observações quantitativas analisadas para fins metodológicos foram obtidas na página on line (www.cepea.esalq.usp.br) do Centro de Estudos Avançados em Economia Aplicada da Escola Superior de Agricultura “Luiz de Queiroz” da Universidade de São Paulo (CEPEA- ESALQ/USP), e referem-se ao valor mensal do preço médio do trigo nacional no Rio Grande do Sul, em reais, durante o período de julho de 2006 a junho de 2016.

Após a verificação do correlograma da série original, da análise da Função de Autocorrelação e Autocorrelação Parcial da série original para concluir se a mesma é estacionária, encontraram-se os modelos concorrentes que explicariam o fenômeno em estudo, efetuou-se a análise dos resíduos buscando-se por modelos que fornecessem ruído branco. O modelo selecionado será aquele que satisfaz os critérios penalizadores AIC e BIC, em que o menor valor destes sinalizará para a escolha do modelo mais propício, ou seja, aquele que apresentará um menor erro para as previsões desejadas. Ainda como critério complementar utilizou-se o Erro Quadrático Médio (EQM), porque, quanto menor o valor encontrado, mais compatível este modelo está com a realidade da série (SOUZA, F. et al., 2010).

O melhor modelo encontrado será utilizado para realizar previsões na intenção de auxiliar na gestão dos custos e estoques das indústrias moageiras de trigo.

4. Análise dos dados e previsão

A indústria moageira trabalha com preços de farinha excessivamente competitivos entre si, tendo como característica deste mercado a facilidade de informações a respeito do preço do concorrente. O trigo é a principal matéria-prima da farinha, representando cerca de 70% do custo de seu faturamento líquido. Nesse contexto, a informação sobre os custos futuros do trigo torna-se de suma importância na gestão dos custos produtivos e estoques de trigo das indústrias moageiras, assim as previsões proporcionam aporte para a gestão da produção.

4.1 Preço do Trigo

Para identificar o modelo apropriado que melhor representa a série de preços do trigo (em reais) o primeiro passo foi a realização da inspeção gráfica para verificar o comportamento da série.

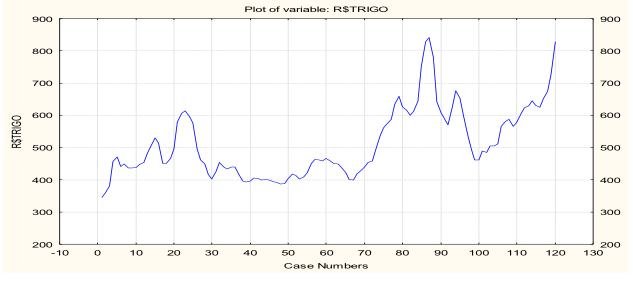
Figura 1- Série original do preço médio do trigo no Rio Grande do Sul de jul/06 a Jun/16.

Observa-se na Figura 1, que a série apresenta uma tendência crescente e picos ao longo do período de análise, características estas de séries não estacionárias.

Como a análise visual não é comprobatória, o segundo passo foi utilizar-se da análise da Função de Autocorrelação e Autocorrelação Parcial da série original para concluir se a mesma é estacionária. A Figura 2 apresenta respectivamente a FAC e FACP da série de preços do trigo, verifica-se que a mesma possui características de não estacionariedade, porque apresenta um decaimento lento da FAC.

Averiguado a existência de não-estacionariedade da série, por meio de uma única diferença, Figura 3, a série passa a apresentar um comportamento estacionário, oscilando em torno de uma média, não sendo necessário mais diferenciações.

Figura 3- Série diferenciada do preço do trigo.

A próxima etapa metodológica é a identificação dos modelos significativos que representam o comportamento da série do preço de trigo no Rio Grande do Sul. Na Tabela 1, observa-se os modelos significativos encontrados, e seus parâmetros. Os modelos apresentados são significativos porque todos apresentam coeficientes com nível de significância (p-value) menor que 5% e respeitam as condições de estacionariedade e invertibilidade, uma vez que seus valores em módulo são menores que um.

Para decidir pelo melhor modelo foram utilizados como base para decisão os Critérios Penalizadores AIC e BIC, esses utilizados para definir os modelos parcimoniosos por meio dos menores valores encontrados.

Como critério complementar utilizou-se o Erro Quadrado Médio (EQM) para testar a confiança do modelo em previsão, sendo que, quanto menor o valor encontrado mais próximo da realidade serão as previsões do modelo.

Tabela 1- Modelos encontrados para a série do preço médio do trigo, RS, jul/06 a Jun/16.

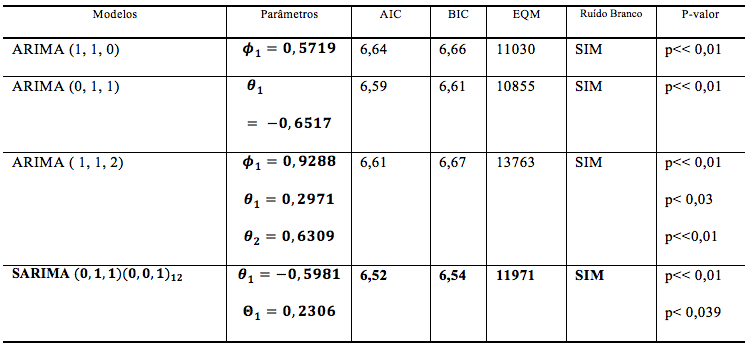
O melhor modelo encontrado foi o SARIMA (0,1,1)(0,0,1)₁₂, este apresentou o menor AIC e BIC, através do Erro Quadrado Médio do modelo verifica-se que este está condizente com a realidade da série. Os resíduos provenientes deste modelo são não-autocorrelacionados, com média zero e variância constante, caracterizando-se, portanto, como ruído branco. A Figura 4 apresentam, respectivamente, a FAC e a FACP dos resíduos do modelo escolhido.

A FAC e a FACP residual do modelo mostra que a autocorrelação dos resíduos estão dentro dos limites de confiabilidade de 95%. Desta forma, esses resíduos são não-autocorrelacionados.

O último passo, após encontrar o modelo adequado, foi aplicá-lo para realizar previsões ex-ante dos preços do trigo no Rio Grande do Sul para um horizonte de seis meses a partir do período de Julho de 2016. Na Tabela 2, é possível visualizar as previsões mensais do preço do trigo de julho a dezembro de 2016, os limites com 95% de confiança e o erro padrão.

Tabela 2- Previsão da série do preço de trigo no RS (em reais), para o período de Jul/16 a Dez/16

Observando-se a Tabela 2, são visualizadas as previsões para os 6 meses posteriores à última informação da amostra. A previsão apresenta valores superiores aos praticados no decorrer do período em análise, porém significativos, dado que o mercado sinaliza para alta de preços devido à escassez de grão de qualidade e necessidade das fábricas de rações que demandaram de trigo para substituir o milho, como já mencionado.

5. Conclusão

Como principal ingrediente na fabricação de massas, pães, biscoitos e outras receitas na nossa alimentação básica de cada dia encontra-se a farinha de trigo. O trigo é a principal matéria-prima da farinha que representa cerca de 70% do custo de seu faturamento líquido, sendo este mercado onde as indústrias moageiras estão inseridas é muito competitivo.

Neste artigo efetuou-se a previsão ex-ante para o preço do trigo utilizando a metodologia Box e Jenkins. Dentre os candidatos o modelo selecionado pela a maioria dos critérios penalizadores foi o SARIMA (0,1,1)(0,0,1)₁₂.

Os resultados encontrados pela previsão para julho a dezembro de 2016 seguem as expectativas já esperadas de aumento dos preços, visto as notícias relatadas pela Abitrigo e Embrapa, sobre a falta do grão.

Portanto, as previsões do preço do trigo propiciam aos gestores das indústrias moageiras do estado do Rio Grande do Sul a antecipação do cenário futuro dos preços do grão e assim poderão servir para uma melhorar a gestão e planejamento, respectivamente, de custos e estoques das suas indústrias moageiras onde estão inseridos.

Referências

ABITRIGO, Associação Brasileira da Indústria do Trigo. Estatísticas. Disponível em: <http://www.abitrigo.com.br/index.php?mpg=02.00.00>. Acesso em: 01/07/ 2016.

ALBUQUERQUE, Aldous Pereira; MORAES, Marcel Castro de. Modelagem Econométrica para a Previsão do Preço Futuro do Cacau: Abordagem ARIMA. Revista Ciências Administrativas (UNIFOR), v. 13, p. 193-207, 2007.

BOX, G. E. P.; JENKINS, G. M.; REINSELL, G. C.. Time series analysis: forecasting and control. 4. Ed., New Jersey: John Wiley & Sons, 2008.

CEPEA, Centro de Estudos Avançados em Economia Aplicada . Série de preços- USP. Disponível em: <http://cepea.esalq.usp.br/trigo/>. Acesso em: 01/07/2016.

EMBRAPA, Empresa Brasileira de Pesquisa Agropecuária. Notícias . Disponível em: <https://www.embrapa.br/soja/cultivos/trigo1>. Acesso em: 02/07/2016.

EHLERS, Ricardo S. Análise de séries temporais: apostila. São Paulo: Departamento de estatística- USP, 2003-2009. 118 f.

GUJARATI, Damodar N. 3. Ed., São Paulo: Pearson Makron Books, 2000.

GREENE, Willian H. Econometric analysis. 5. Ed. New Jersey: Prentice Hall, 2003.

LIMA, A. C.. Precificação na Indústria do Trigo: o custo e a elasticidade como indutores. Custos e @gronegócios on line – ISSN 1808-2882 – v. 1, n. 2, Jul/Dez 2005.

LEMOS, F. O. Metodologia de seleção de métodos de previsão de demanda. 2006. 183 p. Dissertação (Mestrado em Engenharia de Produção) Departamento de Engenharia de Produção e Transportes, Universidade Federal do Rio Grande do Sul, Porto Alegre, 2006.

MONTGOMERY, Douglas C. JENNINGS, Cheryl L. e KULAHCI, Murat. Introduction to time series analysis and forecasting. 3.Ed. New York: John Wiley and Sons, 2008.

MAKRIDAKIS, S.; WHEELWRIGHT, S.; HYNDMAN, R.. Forecasting: methods and aplications. 3.Ed., New York: John Wiley & Sons, 1998.

MORETTIN, P.A.; TOLOI, C.M.C.Modelos de função de transferência. São Paulo: ABE. 1989. V.1. 166p.

SOUZA, Adriano Mendonça; MARCHEZAN, Analice. Previsão do preço dos principais grãos produzidos no Rio Grande do Sul. Santa Maria: Ciência Rural , 2010.

SOUZA, Francisca Mendonça; ALMEIDA, S. G.; GUARNIERI, J. P.;  SOUZA, A. M.; LOPES, Luis Felipe Dias. Previsão do consumo de cimento no estado do Rio Grande do Sul. Pesquisa Operacional para o Desenvolvimento. v.2. p.3- 11; 2010.

1. Acadêmico do curso de Mestrado em Engenharia da Produção- PPGEP da Universidade Federal de Santa Maria (UFSM), Santa Maria, RS, Brasil.
2. Professor, Departamento de Estatística, Universidade Federal de Santa Maria (UFSM), Santa Maria, RS, Brasil. Email: amsouza.sm@gmail.com