HOME | ÍNDICE POR TÍTULO | NORMAS PUBLICACIÓN

Espacios. Vol. 37 (Nº 37) Año 2016. Pág. 19

Aplicação de métodos de previsão de séries temporais em uma indústria têxtil

Aplicación de métodos de previsión de series temporales en una industria textil

Patrícia Budal BRUNATO 1; Elisa HENNING 2; Olga Maria Formigoni Carvalho WALTER 3; Guilherme Luz TORTORELLA 4

Recibido: 12/07/16 • Aprobado: 29/072016

Conteúdo

1. Introdução

2 Referencial teórico

3 Procedimentos metodológicos

4. Resultados e discussão

5 Conclusão

Referências

1. Introdução

O principal desafio de uma organização é manter-se competitiva frente as constantes mudanças do mercado. Dessa forma, o planejamento torna-se uma ferramenta essencial para o gerenciamento de uma empresa.

A gestão da demanda é de grande importância para uma empresa, pois o planejamento da produção é feito com base nos dados estimados nas previsões (FLEURY; BATALHA, 2009). Assim, é essencial que a organização não somente efetue previsões, como tenha conhecimento das variáveis que podem impactar na sua demanda, e consequentemente nos recursos necessários para sua produção.

De acordo com a Associação Brasileira da Indústria Têxtil e de Confecção (ABIT, 2015), durante a última década, o setor têxtil brasileiro tem sofrido constantes alterações. Houve uma perda progressiva de participação de mercado devido ao suprimento da demanda por produtos importados e essa instabilidade faz com que o planejamento das indústrias têxteis se torne ainda mais cauteloso.

Em decorrência da crise econômica que atinge fortemente os setores industriais, incluindo também o setor têxtil, várias foram as expectativas sobre o volume de produção e vendas divulgadas pela ABIT, conforme atestam algumas publicações (O GLOBO, 2015; BOUÇAS, 2016; MOREIRA, 2016; POSSEBON, 2016; SANTAELLA, 2016).   

Notícias recentes apontam que o setor têxtil no Brasil vem sofrendo também os reflexos da crise econômica. O setor que já eliminou mais de 20 mil postos de trabalho, fechou 2015 com desempenho negativo e queda de 5%, prevê crescimento para o ano de 2016. Fatores como aumento dos custos produtivos, especialmente na energia elétrica e impostos, aliado a um cenário de dificuldades, com falta de previsibilidade na economia e mercado interno menos aquecido, além da concorrência com os chineses, tem levado as indústrias têxteis a reavaliar suas estratégias como investir no mercado externo, para estimular a produção (ABIT, 2016; MOREIRA, 2016).

Não é de hoje que o setor têxtil tem sofrido com as variações da economia. Segundo Andrade (2006) o setor sentiu os fortes impactos decorrentes da abertura comercial que ocorreu da década de 1990. Naquela época, o setor que tinha baixa capacidade competitiva, ao se considerar o contexto mundial, apresentou grave crise, deixando o saldo da balança comercial têxtil em US$ 1 bilhão negativos no ano de 1996 seguindo negativo até o ano de 2000. A partir de então as ações de reestruturação tomadas pelo setor começaram a surgir, demonstrando um comportamento de crescimento e estabilidade, em toda a cadeia produtiva. O setor têxtil recuperou-se a partir de 2005 alcançando um resultado superavitário de US$ 668 milhões, o que ainda era considerado modesto mediante ao potencial de toda indústria nacional.

Frente aos desafios encontrados no mercado, o setor têxtil no Brasil tem passado, por um processo de reestruturação significativa de todo o seu complexo produtivo, assim como das formas de gestão destes sistemas produtivos, buscando por tecnologias que venham a auxiliar na tomada de decisões e gerenciamento produtivo. Nesse cenário, de incertezas com relação ao mercado e consequentemente com volume de produção, uma previsão de vendas adequada é necessária para o dimensionamento correto da produção e seus recursos.

No Brasil, poucos trabalhos abordam modelos de previsão de séries temporais com modelos de suavização exponencial e ARIMA para a demanda da indústria têxtil. Bertotti, Caetano e Borges (2003) discutem um modelo de previsão usando Redes Bayesianas na previsão da proporção da primeira estimativa de vendas no lançamento de produtos numa empresa têxtil do Brasil. Barbosa (2007) realiza o planejamento e controle da capacidade produtiva de uma indústria de meias e utiliza suavização exponencial de Holt-Winters, a fim de comparar a previsão e a capacidade produtiva. Guimarães (2008) desenvolve um processo de previsão de demanda apoiado em técnicas quantitativas e qualitativas de previsão a fim de melhorar a qualidade da previsão de demanda que serve como input para o plano de produção de uma empresa têxtil, usando suavização exponencial de Holt-Winters. Girardi (2008) e Girardi, Camargo e Motta (2013) apresentam um modelo de previsão de vendas integrando o modelo de previsão quantitativa de Box & Jenkins com o método qualitativo de julgamento de valor. Milnitz, Marchi e Samohyl (2011) analisam dados de uma indústria têxtil de vestuário infantil, onde foi aplicado o método de Holt-Winters. Ekami, Ming e Brito (2014) demonstram como a utilização da previsão da demanda pode ser utilizada como ferramenta estratégica na indústria de vestuário.  Reis (2014) avaliou técnicas de suavização exponencial, modelos ARIMA, regressão e redes neurais artificiais otimizadas pela técnica de algoritmos genéticos para examinar quais delas apresentam maior acurácia quando aplicadas na previsão de vendas em uma indústria brasileira do segmento têxtil.

Assim, este trabalho tem como objetivo o desenvolver um modelo de previsão de vendas para uma indústria têxtil, por meio da aplicação de métodos de previsão de séries temporais. Busca-se o desenvolvimento de um modelo de alta qualidade, a fim de construir uma previsão de melhor desempenho que a existente. A pergunta de pesquisa que se busca solucionar é: Por meio da aplicação de modelos estatísticos, é possível desenvolver modelos de previsão com menores discrepâncias do que o método atual utilizado pela empresa?

Este artigo está estruturado a partir desta introdução em quatro seções. A segunda seção apresenta a fundamentação teórica. A terceira seção é dedicada à metodologia da pesquisa. Na quarta seção, estão os resultados e discussão. Na última seção, são apresentadas as conclusões e sugestões para trabalhos futuros.

2. Referencial teórico

Nesta seção é abordado inicialmente um panorama do setor têxtil e são também apresentados os temas: séries temporais, métodos de previsão de vendas de séries temporais – com ênfase nos modelos de suavização exponencial e autorregressivo integrado de média móvel (ARIMA).

2.1 Panorama geral do setor têxtil

O setor têxtil é um dos mais tradicionais do país, tendo iniciado suas atividades no final do século XIX. Por muito tempo, esse setor experimentou um protecionismo que garantia que, independente das condições ou práticas comerciais, as empresas permanecessem competitivas no mercado. A partir da década de 1990, com a queda das barreiras tarifárias, a indústria vivenciou um período crítico, quando passou a competir com indústrias internacionais, e, portanto, passou a intensificar a atenção a fatores como a produtividade e qualidade dos produtos (AZEVEDO, 1997).

A globalização permitiu que grande parte da produção mundial fosse deslocada para países emergentes em busca de redução no custo de produção, especialmente referente à mão de obra (COSTA; ROCHA; 2009).  Em 2012, China e Hong Kong foram os principais produtores, com o equivalente a 54,0% da produção mundial. O Brasil ocupou a quinta posição no ranking dos maiores produtores de manufaturas têxteis, respondendo por 2,7% do total produzido (ABIT, 2015).

O setor têxtil tem uma grande participação na economia nacional, representando 5,7% do valor total da produção da indústria da transformação. Apesar de ser um grande produtor e consumidor de produtos têxteis, o Brasil tem sua participação no mercado mundial reduzida, representando aproximadamente 0,5% dos exportadores (ABIT, 2015). Para que possa ter um valor mais expressivo no mercado internacional, é necessário o desenvolvimento de novas políticas e estratégias competitivas.

Com relação ao mercado interno, nota-se que houve um aumento do consumo nos últimos anos, acompanhada de uma queda da produção têxtil no Brasil. Isso representa a perda de participação da indústria nacional, que tem sua demanda sendo substituída progressivamente por produtos importados (ABIT, 2015). O resultado da balança comercial evidencia esse fato: entre 2009 e 2013, houve uma queda 22,3% ao ano nas exportações. Em contrapartida, no mesmo período, as importações cresceram de 30,2% ao ano (IEMI, 2014).

Mediante o contexto do cenário atual do setor, é imprescindível para as indústrias têxteis que realizem um planejamento capaz de manter a empresa competitiva no mercado. Desta forma, a previsão de vendas mostra-se como uma ferramenta eficaz para auxiliar no desenvolvimento do planejamento estratégico da empresa, assim como melhorar o dimensionamento dos recursos produtivos.

2.2 Previsão de vendas

A previsão é uma predição de um evento futuro (MONTGOMERY; JENNINGS, KULAHCI, 2008). Ela é parte integral da tomada de decisão gerencial de uma organização. A necessidade de predizer tem aumentado ao longo dos anos, visto a incerteza dos mercados e aumento de concorrentes em todos os setores.

Elaborar previsões é uma atividade que atinge diversos setores de uma indústria. Seus resultados são utilizados para o planejamento da produção, para dimensionar as atividades, definir os recursos humanos e materiais necessários, e realizar o controle de estoques (MONTGOMERY; JENNINGS; KULAHCI, 2008). A relação entre os diversos departamentos de uma empresa e a previsão de vendas está descrita na Figura 1.

Essas previsões também podem ser aplicadas para realizar o planejamento e controle financeiro da empresa. A partir desse planejamento financeiro, a organização avalia os resultados esperados e define um plano de ações para atingir esses resultados.

De acordo com a Figura 1, nota-se a relevância do desenvolvimento de previsões para o planejamento estratégico da organização como um todo, assim como seu impacto em cada setor.  Reconhecer a relevância de realizar previsões no contexto organizacional e gerencial é tão importante quanto a seleção do método de previsão em si (MAKRIDAKIS; WHEELWRIGHT; HYNDMAN, 1998).

Figura 1 – Fluxo de informação entre as previsões de vendas e o planejamento do negócio

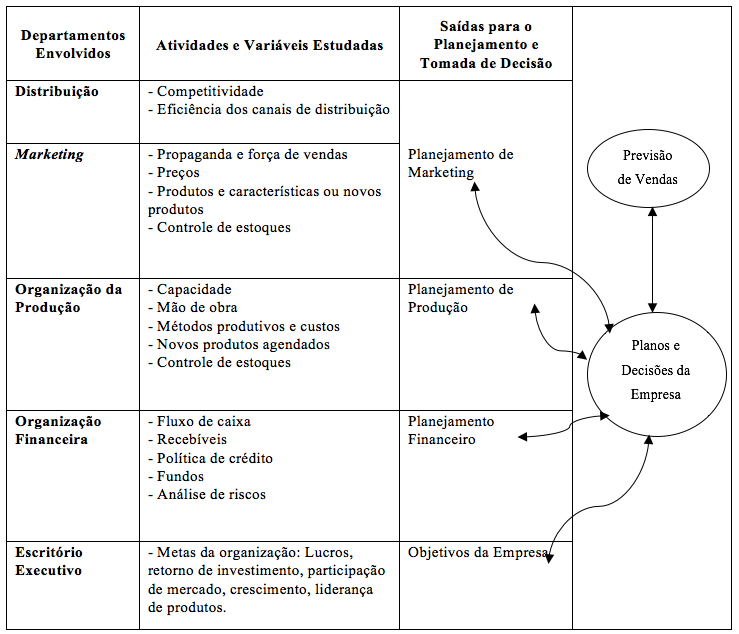
Fonte: Adaptado de Makridakis, Wheelwright e Hyndman (1998)

Atualmente, existem diversos métodos de previsão, variando de métodos simples e intuitivos aos mais complexos e quantitativos (MORETTIN; TOLOI, 2006). Segundo Makridakis, Wheelwright e Hyndman (1998), os métodos de previsão variam de acordo com o seu horizonte de previsão, tipos de padrões de dados, entre outros aspectos.  Existem duas grandes categorias que separam os diversos métodos existentes: os métodos qualitativos e os métodos quantitativos. A Figura 2 sintetiza as técnicas de previsão de vendas.

Os métodos qualitativos são de natureza subjetiva e requerem a opinião de profissionais experientes. São utilizados quando a quantidade de dados é insuficiente ou inexistente, como por exemplo, a introdução de um novo produto no mercado. Em contrapartida, os métodos quantitativos são utilizados quando há informação quantitativa disponível, promovendo o desenvolvimento dos modelos a partir de dados históricos (MONTGOMERY; JENNINGS; KULAHCI, 2008). 

Figura 2: Classificação dos métodos de previsão de vendas

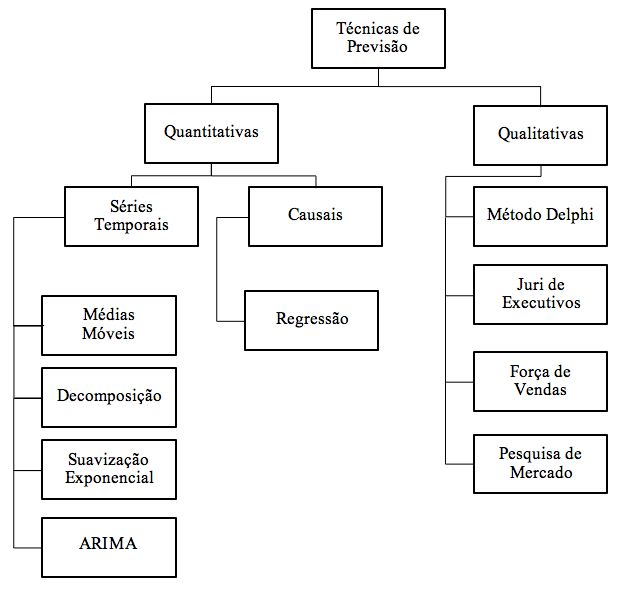
Fonte: Adaptado de Corrêa e Corrêa (2006).

Os métodos quantitativos podem, ainda, ser classificados em econométricos ou de séries temporais (MORETTIN; TOLOI, 2006). Os métodos econométricos assumem que a variável a ser predita apresenta uma relação causal com outras variáveis. Já os métodos de séries temporais, estimam as previsões utilizando apenas os dados históricos, sem considerar possíveis variáveis causais (MONTGOMERY; JENNINGS; KULAHCI, 2008).

De acordo com Makridakis, Wheelwright e Hyndman (1998), ambos os métodos econométricos e de séries temporais têm vantagens distintas que variam de acordo com a situação. Modelos causais devem ser utilizados para definição de estratégias, enquanto modelos de séries temporais devem ser aplicados para realizar previsões.

Neste artigo serão utilizados os métodos quantitativos de séries temporais, visto que a empresa possui uma quantidade representativa suficiente de dados históricos válidos que viabilizam esta análise. Sabe-se que um erro na escolha do método de previsão pode acarretar em grandes prejuízos para a empresa, visto que a previsão é a base do seu planejamento estratégico. Dessa forma, a seleção e a aplicação do método correto são imprescindíveis para o desenvolvimento de uma previsão com acurácia.

O desenvolvimento de um modelo para previsão de vendas apresenta basicamente cinco etapas. A primeira etapa do processo de previsão de vendas engloba a definição do problema; na segunda, deve ser realizada a coleta de dados históricos. A seguir, efetua-se a análise exploratória dos dados. O objetivo dessa etapa é identificar quais métodos de previsão são adequados para a série apresentada. Na quarta etapa, realiza-se a seleção e ajuste do modelo, observando-se as suposições necessárias.  Na última etapa, o modelo escolhido pode ser utilizado para predizer as vendas da organização.

2.3 Séries temporais

Segundo Ehlers (2009, p. 1) “uma série temporal é uma coleção de observações feitas sequencialmente ao longo do tempo”. A principal característica desse tipo de conjuntos de dados é que suas observações são relacionadas, e que é possível analisar e modelar esta relação para estimar como essas observações se comportarão no futuro. Os modelos que descrevem as séries temporais são processos estocásticos, controlados por leis probabilísticas.

As séries temporais possuem três componentes básicos: tendência, sazonalidade e ciclo (SAMOHYL; SOUZA; MIRANDA, 2008). A tendência ocorre quando há um crescimento ou decrescimento nos dados, a longo termo. A sazonalidade existe quando a série é influenciada por fatores sazonais, como um período específico do ano, o mês, ou dia da semana, por exemplo. Já o ciclo, ocorre quando os dados variam em um período arbitrário. A principal diferença entre a sazonalidade e o ciclo é que o último não apresenta constância de ocorrência, como a sazonalidade (MAKRIDAKIS, WHEELWRIGHT; HYNDMAN, 1998).

Existem diversos métodos estatísticos de previsão de séries temporais. A seleção dos métodos e construção dos modelos depende de diversos fatores, como o comportamento do fenômeno e o objetivo da análise (MORETTIN; TOLOI, 2006). Dentre eles, podemos destacar suavização exponencial, e modelos autorregressivos integrados de médias móveis (ARIMA), que são utilizados para desenvolver os modelos desta pesquisa. 

2.4 Métodos de suavização exponencial

De acordo com Samohyl, Souza e Miranda (2008), os métodos de previsão por suavização exponencial (SE) consistem na decomposição da série temporal nos parâmetros tendência e sazonalidade, ponderando seus valores passados e os desvalorizando em relação aos valores mais recentes. Esses modelos aceitam a hipótese que os valores extremos da série temporal representam a aleatoriedade, e que, portanto, por intermédio da suavização desses extremos é possível definir o padrão básico da série (MORETTIN; TOLOI, 2006).

Dentre esses métodos, quatro são os mais conhecidos: o método das Médias Móveis Simples, a Suavização Exponencial Simples, a Suavização Exponencial de Holt e a Suavização Exponencial Sazonal de Holt-Winters. Estes métodos e suas principais características são descritos brevemente a seguir com base em Makridakis, Wheelwright e Hyndman (1998), Morettin e Toloi (2008), Samohyl, Souza e Miranda (2008), e Montgomery, Jennings e Kulahci (2008).

O método de Médias Móveis Simples pode ser considerado o mais ingênuo dentre os métodos desta categoria. Ele consiste em calcular a média aritmética das observações. O termo “média móvel” é utilizado porque a cada nova observação, uma nova média pode ser computada, substituindo o dado mais antigo pelo mais novo. Sua principal desvantagem é que só pode ser utilizado em séries estacionárias.

A Suavização Exponencial Simples  pode ser descrita por uma média ponderada que atribui pesos maiores às observações mais recentes, em relação às observações anteriores que têm seu peso decaído exponencialmente. Assim como o método anterior, a Suavização Exponencial Simples não considera a tendência e a sazonalidade da série. Em 1957, Holt expandiu este método para séries com tendência linear, denominado como método de Suavização Exponencial de Holt, que  considera duas constantes para realizar a previsão: nível (α) e crescimento (β) que variam entre 0,01 e 0,99 (SOUZA et al., 2008).

Em 1960 Winters aprimorou o método desenvolvido por Holt, permitindo que o mesmo fosse utilizado em séries com tendência e sazonalidade. O método, conhecido como Holt-Winters, passou a incluir a constante de sazonalidade. Na prática, Holt desenvolveu dois métodos diferentes, um para sazonalidade aditiva (a sazonalidade é somada à tendência da série) e outro para sazonalidade multiplicativa (a sazonalidade é multiplicada pela tendência). 

Hyndman et al. (2002) sugerem uma nomenclatura específica para a classificação dos métodos de suavização exponencial, conforme Quadro 1. A primeira letra representa a tendência, enquanto a segunda a sazonalidade. A letra “N” indica que o parâmetro é inexistente. A letra “A” corresponde à aditivo, enquanto a “M” corresponde à multiplicativo. Caso a tendência seja amortecida (tendências não lineares), a classificação conterá a letra “a”. Por exemplo, o modelo AA apresenta tendência e sazonalidade aditivas.

Quadro 1 – Classificação dos métodos de SE quanto à tendência e sazonalidade

Fonte: Adaptado de Hyndman et al. (2008).

É possível considerar também o tipo de erro do modelo: aditivo (A) ou multiplicativo (M). Nesta nomenclatura, a primeira letra denota o tipo de erro, a segunda letra remete à tendência e a terceira letra corresponde à sazonalidade, por exemplo: ANM seria um modelo com erro aditivo, nenhuma tendência e sazonalidade multiplicativa.

2.5 Método arima

De acordo com Makridakis, Wheelwright e Hyndman (1998), o método ARIMA surgiu a partir da junção do método autorregressivo (AR) com o de média móvel (MA), que resultava primariamente no método autorregressivo de média móvel (ARMA). Entretanto, esse modelo poderia ser utilizado somente para séries estacionárias, ou seja, que se desenvolvem aleatoriamente ao longo do tempo. Com o intuito de estender seu uso para séries não estacionárias, foi incorporado ao modelo um parâmetro de diferenciação da série (I), resultando por fim, no processo autorregressivo integrado de média móvel.

Na sequência serão abordados os modelos ARIMA não sazonal, o ARIMA sazonal e o ARIMA com drift com base em Box, Jenkins e Reinsel (1994), Makridakis, Wheelwright e Hyndman (1998), Morettin e Toloi (2006) e Hyndman e Athanasopoulos (2013).

O modelo geral é conhecido como ARIMA (p, d, q), onde: p representa a ordem da parte autorregressiva, d é referente ao processo de diferenciação envolvido, e q representa o processo de média móvel. Contudo, sua utilização requer um maior conhecimento estatístico e depende da análise correta dos dados para uma estimação correta dos parâmetros do modelo. 

Para a estimação do parâmetro autorregressivo (p), é necessário analisar a função de autocorrelação parcial (PACF), que mede o grau de associação entre as variáveis nos instantes t e t-k, quando os efeitos das outras defasagens (1, 2, 3, ..., k - 1) são removidos. Em relação ao processo de diferenciação (d), é necessário identificar, primeiramente, se a série apresenta comportamento estacionário ou não. Esta análise pode ser feita a partir do gráfico da série temporal.   O gráfico da função de autocorrelação (ACF) também pode ser examinado, já que em séries estacionárias os valores tendem à zero rapidamente. Além da análise gráfica, também pode ser realizado o teste da raiz unitária, que determina se a diferenciação é necessária ou não. Como exemplo, pode-se citar o teste de Dickey-Fuller. Já o processo de média móvel q, pode ser estudado a partir da ACF da série. A ordem mais adequada, neste caso, está relacionada com a mais alta defasagem antes das observações decaírem abruptamente.

O modelo geral representado como ARIMA (p, d, q) adquire uma componente sazonal, tornando-se ARIMA(p, d, q) (P, D, Q)m , onde m representa o número de períodos de sazonalidade. Esses modelos são conhecidos também como Seasonal Autoregressive Integrated Moving Average (SARIMA).

A parte sazonal do modelo pode ser identificada por meio dos picos nos gráficos de PACF e ACF. Um modelo ARIMA (0,0,0) (0,0,1)₁₂, por exemplo, no seu gráfico de ACF, apresentará picos no período 12, e não terá outros picos significativos. Já no gráfico de PACF, ele apresentará um decaimento exponencial nos picos múltiplos que representam a sazonalidade (12, 24, 36, ...). Em alguns casos, pode ser necessário realizar diferenciações sazonais na série, com o objetivo de torná-la estacionária.

De acordo com Cribari Neto (1990, p. 382) por intermédio do teorema de Beveridge-Nelson “(...) qualquer série que possa ser modelada através de um ARIMA (p,d,q) (...) possui uma tendência estocástica do tipo passeio casual com drift”.  Neste caso, o drift representa uma tendência linear existente na série, que pode ser positiva ou negativa. A inclusão do drift possibilita que essa tendência seja representada no modelo por meio de uma constante (HYNDMAN, 2014). É importante ressaltar que, segundo Hyndman (2014), mesmo séries diferenciadas podem conter constantes de tendências, e que o pesquisador deve determinar a necessidade de incluí-las no modelo.

De acordo com a metodologia desenvolvida por Box e Jenkins, um ciclo iterativo de atividades deve ser seguido para a escolha da estrutura do modelo ARIMA a ser elaborado. A primeira etapa corresponde à identificação do modelo, e compreende a preparação dos dados e análise exploratória, incluindo a construção dos correlogramas (ACF e PACF) para identificação de modelos potenciais. Nessa etapa também é realizada a diferenciação da série, caso necessário, até que a série torne-se estacionária. Já a segunda etapa, refere-se à estimação dos parâmetros do modelo.

​2.6 Adequação e seleção do modelo

De acordo com Morettin e Toloi (2006), após a estimação do modelo, é necessário constatar se este representa adequadamente os dados, mediante alguns critérios que devem ser satisfeitos. Essa verificação pode ser realizada a partir dos resíduos do modelo.

Primeiramente, os resíduos do modelo não devem ser correlacionados. Essa condição pode ser analisada por meio dos correlogramas, onde os resíduos devem ter as características de um ruído branco, ou seja, os valores plotados não ultrapassam os limites de controle do correlograma. Makridakis, Wheelwright e Hyndman (1998) sugerem que, além da análise gráfica, também sejam realizados testes de hipóteses Box-Pierce e Ljung-Box.

Na sequência, deve ser analisada a variância dos resíduos. Eles devem ter variância constante, caso contrário, os testes de hipótese utilizados para interpretar os outros parâmetros podem ter sua confiabilidade alterada (SOUZA, 2005). Esta característica pode ser analisada a partir dos correlogramas, pois se os resíduos forem um ruído branco, significa que têm a variância constante. Por fim, deve-se verificar se os resíduos seguem a distribuição normal, nesse caso, podem ser aplicados testes de normalidade, como o teste Shapiro-Wilk.

 A seleção de um modelo pode ser realizada com base nos critérios de informação e a partir das medidas dos erros de previsão. De forma genérica, um erro de previsão é a diferença entre o valor previsto (Pt) e o valor observado (Ot). A seguir são descritas as medidas aplicadas nesta pesquisa, com base em Makridakis, Wheelwright e Hyndman (1998) e Samohyl, Souza e Miranda (2008).

3. Procedimentos metodológicos

Esta pesquisa é classificada como exploratória descritiva, pois pretende compreender o relacionamento entre variáveis, e ampliar o conhecimento a respeito do problema, buscando identificar um modelo de previsão de vendas de alta qualidade, a fim de construir uma previsão de melhor desempenho que a existente na empresa analisada. Esta pesquisa também pode ser definida como aplicada, visto que tem como objetivo o estudo de dados reais de uma empresa para a solução do problema (PINHEIRO, 2010).

Este artigo aborda os processos de previsão quantitativos, por meio do uso de métodos estatísticos. Os dados foram coletados diretamente no departamento comercial de uma indústria têxtil, que realiza o controle desses dados a partir de um software de gestão empresarial. Foram coletados dados mensais dos últimos seis anos (72 observações) da empresa para o desenvolvimento da previsão, compreendendo o período de 2009 à 2014. Os dados dos sete primeiros meses de 2015 também foram reunidos para o cálculo da acurácia das previsões fora da amostra.  

Para o tratamento estatístico dos dados foi utilizado o software R (R CORE TEAM, 2015) com auxílio do pacote “forecast” (HYNDMAN; KHANDAKAR, 2008), específico para previsões com séries temporais.

4. Resultados e discussão

Conforme Figura 3, que apresenta os dados observados da série de vendas da empresa no período da amostra, bem como a série decomposta, pode-se afirmar que a série apresenta sazonalidade por conferir um padrão repetitivo, com frequência mensal e sugere-se uma leve tendência positiva de crescimento.

Por apresentar sazonalidade e tendência, surge a suposição de que a série pode ter caráter não estacionário. Foram aplicados os testes de estacionariedade de Dickey-Fuller (p-valor = 0,01) e Phillips-Perron (p-valor = 0,01) indicados por Hyndman e Athanasopoulos (2013) e ambos rejeitaram a hipótese de que a série é não estacionária com nível de significância de 5%.

Como a série apresenta sazonalidade, o método de suavização exponencial mais adequado é o de Holt-Winters. A função “ets”, do pacote forecast (Hyndman et al., 2008), retornou um modelo ANA, com erro aditivo, sem tendência e com sazonalidade aditiva.  Os resíduos do modelo se apresentaram como um ruído branco, sem autocorrelação e normalmente distribuídos (teste de Shapiro-Wilk p-valor = 0,1671), portanto adequado para realizar previsões.

Figura 3 – Gráfico da série original e decomposta

Fonte: Primária (2016)

A eficácia dos modelos ARIMA (p, d, q) depende diretamente da estimação dos parâmetros p, d, e q mais adequados à série. A análise exploratória revelou que a série em análise apresenta padrão estacionário. Em relação a definição do processo autorregressivo (AR) e ao processo de média móvel (MA), representados pelos parâmetros p e q foram analisados os gráficos ACF e PACF da série, representado na Figura 4.

Figura 4: Gráfico de autocorrelação (esquerda) e autocorrelação parcial (direita) da série.

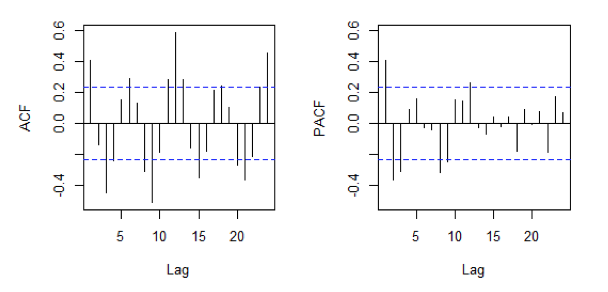
Fonte: Primária (2016)

De acordo com Morettin e Toloi (2006) um processo ARMA (p, q) apresentará ACF com infinita extensão, com decaimento exponencial ou senoidal amortecido após q, e PACF representado por exponenciais ou senóides amortecidas, com decaimento abrupto após p. Assim, conforme a Figura 4 sugere-se que dois modelos possíveis para os dados sejam um ARIMA (2,0,1) ou um ARIMA (1,0,1). Entretanto, esta análise gráfica dos parâmetros deve ser vista como preliminar, e outros modelos potenciais devem também ser analisados. Como o gráfico de PACF aponta para uma componente sazonal com m =12 os modelos terão a notação ARIMA (p, d, q)_m (HYNDMAN; ATHANASOPOULOS, 2013). 

De acordo com Makridakis, Wheelwright e Hyndman (1998), um dos problemas ao utilizar o método ARIMA refere-se ao grande número de modelos plausíveis. Em relação à série utilizada neste artigo, diversos modelos testados foram adequados para realizar previsões, o que dificulta a escolha. Hyndman e Athanasopoulos (2013) sugerem que sejam comparados os critérios AIC, AICc e BIC para avaliar a qualidade de um modelo. Quanto menores os valores destes critérios, maior a qualidade do modelo. Assim, o modelo ARIMA sazonal (1,0,0) (0,1,1)12 foi selecionado, dentre outros modelos ARIMA analisados, por apresentar os menores valores de AIC = 1.890,68; AICc =1.891,40 e BIC = 1.899,05.

 Para a escolha, também foram avaliadas as medidas de erros de previsão e o comportamento dos resíduos. Entre modelos com medidas similares, escolheu-se o mais parcimonioso, ou seja, com menos parâmetros na equação.  Os resíduos não apresentam autocorrelação e são normalmente distribuídos (teste de Shapiro-Wilk p-valor = 0,2550). Os gráficos de autocorrelação e autocorrelação parcial do modelo têm característica de um ruído branco, como se pode observar na Figura 5.

Figura 5 – ACF e PACF do modelo ARIMA (1,0,0) (0,1,1)₁₂ com drift

Fonte: Primária (2016)

Os valores estimados para os parâmetros do modelo SARIMA são apresentados na Tabela 1.

Tabela 1 – Parâmetros do modelo ARIMA (1,0,0) (0,1,1)₁₂ com drift

Fonte: Primária (2016)

Após a aplicação das técnicas de Suavização Exponencial e ARIMA foi possível identificar um modelo de cada, quando comparado aos outros modelos desenvolvidos pelo mesmo método. Foi necessário confrontar também os dois modelos selecionados de métodos distintos, com o intuito de selecionar o mais eficaz. Na Tabela 2 estão os valores dos erros de previsão dos dois modelos pré-selecionados.

Tabela 2 – Comparação dos erros do modelo SARIMA e SE

Fonte: Primária (2016)   

Ao se comparar, a partir das medidas dos erros de previsão, o modelo resultante da Suavização Exponencial e o ARIMA, é selecionado o ARIMA (1,0,0) (0,1,1)₁₂ com drift, que possui menor valor de MAPE e maior valor de U de Theil. Este modelo é aplicado na previsão de vendas para os sete primeiros meses do ano de 2015. Os valores preditos, observados e respectivos erros estão na Tabela 3. Os valores preditos foram comparados aos valores observados, com o intuito de quantificar a discrepância entre estas medidas.

Tabela 3 – Valores de previsão do modelo ARIMA (1,0,0) (0,1,1)₁₂ com drift

Fonte: Primária (2016)

A Figura 6 apresenta graficamente a previsão do modelo SARIMA, com a linha tracejada representando os valores estimados.

Figura 6 – Gráfico da previsão para modelo ARIMA (1,0,0) (0,1,1)₁₂ com drift.

Fonte: Primária (2016)

Para calcular a previsão, a empresa utiliza dados passados, variando entre dois a três anos. Complementam esses valores, uma meta de crescimento das vendas, resultando assim na previsão estimada, encaminhada para os gerentes e diretores, que, de acordo com a sua opinião e expectativa de mercado, realizam ajustes.  Na Figura 7 está um gráfico com as previsões feitas com o método atual, o modelo proposto e dados referentes ao ano de 2015.  

Figura 7 – Comparação entre os valores observados e as previsões

Fonte: Primária (2016)

Por meio da Figura 7 é possível observar que os valores da previsão do modelo proposto estão mais próximos dos valores observados, representando a melhor opção para realizar previsões.

5. Conclusão

Este artigo foi desenvolvido com o objetivo de desenvolver um modelo de previsão de vendas para uma indústria têxtil, por meio da aplicação de métodos de previsão de séries temporais. Buscou-se evidenciar que por meio da aplicação de métodos estatísticos de previsão de séries temporais que a indústria analisada será capaz de realizar previsões mais acuradas.

Para o desenvolvimento dos modelos, foram utilizados os métodos de Suavização Exponencial e a metodologia ARIMA de Box-Jenkins. Após análises, um modelo de Suavização Exponencial de Holt-Winters com erro aditivo, sem tendência, e com sazonalidade aditiva foi selecionado. Já a metodologia Box-Jenkins apontou diversos modelos como adequados. Ao final, selecionou-se um modelo SARIMA (1,0,0)(0,1,1)₁₂com drif, que apresentou melhor desempenho,  quando comparado ao modelo selecionado pelo método de Holt-Winters e confrontado também com o modelo de previsão atualmente utilizado pela empresa. Pode-se afirmar que o modelo selecionado evidencia uma melhor opção de previsão para a empresa, visto que apresenta menores erros de previsão. A redução dos erros de previsão é de grande valia para a empresa, visto que seu planejamento estratégico é fundamentado de acordo com os resultados esperados a partir da previsão de vendas.

Como continuidade deste trabalho, sugere-se que a empresa passe a monitorar a qualidade de suas previsões. O monitoramento das previsões é tão importante quanto seu desenvolvimento, pois esse acompanhamento permite identificar o momento em que o modelo de previsão deixa de representar o comportamento dos dados de forma coerente. Sugere-se também, que sejam realizados estudos relacionando a capacidade produtiva da indústria com a previsão de demanda desenvolvida neste artigo.

Referências

ABIT. Associação Brasileira da Indústria Têxtil e de Confecção. O Poder da Moda: cenários, desafios e perspectivas. São Paulo: 2015.

AZEVEDO, G. H. W. A Indústria Têxtil Brasileira: Desempenho, Ameaças e Oportunidades. 1997. 88f. Dissertação. (Mestrado em Administração) – Instituto de Pós-Graduação e Pesquisa em Administração - Universidade Federal do Rio de Janeiro, Rio de Janeiro, 1997.

BOX, G. E. P.; JENKINS, G. M.; REINSEL, G. C. Time Series Analysis: forecasting and control. Englewood Cliffs: Prentice Hall, Inc., 1994.

COSTA, A. C. R.; ROCHA, E. R. P. Panorama da Cadeia Produtiva Têxtil e de Confecções e a Questão da Inovação. BNDES. BNDES Setorial. Rio de Janeiro, n. 29, p. 159-202, 2009.

CRIBARI NETO, F. O comportamento estocástico do produto no Brasil. Pesquisa e Planejamento Econômico, v. 2, p. 381-402, ago. 1990.

EHLERS, R. S. Análise de Séries Temporais. 5. ed. 2009. Disponível em: <http://www.icmc.usp.br/~ehlers/stemp/stemp.pdf>. Acesso em: 26 abr. 2016.

FLEURY, A.; BATALHA, M. O. Introdução à Engenharia de Produção. Rio de Janeiro: Campus, 2008.

GIL, A. C. Como Elaborar Projetos de Pesquisa. 4. ed. São Paulo: Atlas, 2002.

HYNDMAN, R. J. Testing for trend in ARIMA models. 2014. Disponível em: < http://robjhyndman.com/hyndsight/arima-trends/>. Acesso em: 10 abr. 2016.

HYNDMAN, R. J.; ATHANASOPOULOS, G. Forecasting: principles and practice. 2013. Disponível em: <https://www.otexts.org/fpp/>. Acesso em: 10 mar. 2016.

HYNDMAN, R. J.; KANDAKHAR, Y. Automatic time series forecasting: the forecast package for R. Journal of Statistical Software, v. 26, n. 3, p. 1-22, 2008.

HYNDMAN, R. J.; KOEHLER, A. B.; ORD, J. K.; SNYDER, R. D. Forecasting with Exponential Smoothing: the state space approach. Berlin: Springer, 2008.

HYNDMAN, R. J.; KOEHLER, A. B.; SNYDER, R. D.; GROSE, S. A state space framework for automatic forecasting using exponential smoothing methods. International Journal of Forecasting, v. 18, p. 439-454, set. 2002.

IEMI. Instituto de Estudos e Marketing Industrial. Mercado Potencial de Cama, Mesa, Banho e Decorativos. São Paulo, 2014.

MAKRIDAKIS, S.; WHEELWRIGHT, S. C.; HYNDMAN, R. J. Forecasting: methods and applications. 3. ed. United States: John Wiley & Sons, Inc., 1998.

MONTGOMERY, D. C.; JENNINGS, C. L.; KULAHCI, M. Introduction to Time Series Analysis and Forecasting. Hoboken: John Wiley & Sons, Inc., 2008.

MORETTIN, P. A.; TOLOI, C. M. C. Análise de Séries Temporais. São Paulo: Blücher, 2006. 

PINHEIRO, J. M. S. Da Iniciação Científica ao TCC Uma Abordagem para os cursos de Tecnologia. Rio de Janeiro: Ciência Moderna, 2010.

R CORE TEAM. R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. Disponível em: <http://www.R-project.org>. Acesso em: 15 abr. 2016.

SAMOHYL, R. W; SOUZA, G. P.; MIRANDA, R. G. Métodos Simplificados de Previsão Empresarial. Rio de Janeiro: Ciência Moderna, 2008.

SOUZA, G. P. Previsão do Consumo Industrial de Energia Elétrica no Estado de Santa Catarina, 2005. 145f. Dissertação (Mestrado em Engenharia de Produção). Universidade Federal de Santa Catarina, Florianópolis.

WESTON, J. F.; BRIGHAM, E. F. Fundamentos da Administração Financeira. 10. ed. São Paulo: Pearson Makron Books, 2000.

ANDRADE, G. J. P. O. Um método de diagnóstico do potencial de aplicação da manufatura enxuta na indústria têxtil. 2006. 298f. Tese. (Doutorado em Engenharia de Produção) – Programa de Pós-graduação em Engenharia de Produção - Universidade Federal de Santa Catarina, Florianópolis, 2006.

BARBOSA, C. S. Aplicação do planejamento e controle de capacidade em uma indústria de meias: análise de produção e demanda. 2007. 42f. Trabalho de Conclusão de Curso (Graduação) - Departamento de Engenharia de Produção, Universidade Federal de Juiz de Fora, Juiz de Fora, 2007.

BERTOTTI, S.; CAETANO, M. L. S.; BORGES, P. S. S. Previsão de vendas para artigos de confecção utilizando redes bayesianas – um caso prático. In: Encontro de Estudantes de Informática do Tocantins. Palmas, 5., 2003.Tocantis,  Anais ... p. 221-226, 2003. 

BOUÇAS, C. Principais riscos à indústria têxtil estão no Brasil, diz ABIT. Valor Econômico. Disponível em: http://www.valor.com.br/empresas/3873644/principais-riscos-industria-textil-estao-no-brasil-diz-abit. Acesso em: 12 Abr. 2016.

EKAMI, K. H. O.; MING, W. C.; BRITO, J. F. S. Ferramentas para a indústria de vestuário: previsão de demanda. In: Congresso Científico Têxtil e de Moda, 2., 2014. São Paulo, Anais... São Paulo, 2014.

CORRÊA, H. L.; CORRÊA, C. A. Administração de produção e operações: manufatura e serviços: uma abordagem estratégica. 2. ed. São Paulo: Atlas, 2006.

GIRARDI, G. Modelo integrado para previsão de vendas como uma ferramenta de competitividade: um estudo de caso em uma empresa do setor têxtil. 2008. 139 f. Dissertação (Mestrado em Administração) – Programa de Pós-Graduação em Administração - Universidade de Caxias do Sul, Caxias do Sul, 2008.

GIRARDI, G.; CAMARGO, M. E.; MOTTA, M. E. E.  Previsão de vendas através de modelos integrados: o caso do setor têxtil de uma empresa. In: Simpósio de Administração da Produção, Logística e Operações Internacionais, 16., Anais ... São Paulo, 2013.

GUIMARÃES, P. L. Processo de previsão de demanda para empresa têxtil. 2008. 113 f. Trabalho de Conclusão de Curso (Graduação) - Universidade de São Paulo, São Paulo, 2008.

IEMI. Instituto de Estudos e Marketing Industrial. Estudo do Mercado Potencial. Roupas de Cama, Mesa, Banho e Decorativos. São Paulo, 2015.

MILNITZ, D.; MARCHI, J. J. SAMOHYL, R. W. Previsão da demanda: uma aplicação do método Holt Winters em uma indústria têxtil de grande porte. In: Encontro Nacional de Engenharia de Produção, 31., 2011. Belo Horizonte, Anais... Belo Horizonte, 2011.

MOREIRA, M. Agência Brasil. Indústria têxtil prevê retomada de crescimento só em 2016. Disponível em: <http://agenciabrasil.ebc.com.br/economia/noticia/2015-01/industria-textil-preve-retomada-de-crescimento-so-em-2016>. Acesso em: 12 Abr. 2016.

O GLOBO. Indústria têxtil prevê queda de 7% nas vendas em 2015. Disponível em: http://oglobo.globo.com/economia/industria-textil-preve-queda-de-7-nas-vendas-em-2015-15121382. Acesso em: 12 Abr. 2016.

POSSEBON, D. Setor de confecção está cauteloso para o inverno 2016. Portal Clica Tribuna. Disponível em:  http://www.clicatribuna.com/noticia/economia/setor-de-confeccao-esta-cauteloso-para-o-inverno-2016-16148 Acesso em: 12 Abr. 2016.

SANTAELLA, T. Indústria têxtil de SC começa 2016 com mais de 500 demissões. Diário Catarinense. Disponível em: http://jornaldesantacatarina.clicrbs.com.br/sc/noticia/2016/01/industria-textil-de-sc-comeca-2016-com-mais-de-500-demissoes-4960132.html. Acesso em: 12 Abr. 2016.

REIS, F. D. Avaliação de modelos de previsão de vendas a partir da exploração de técnicas de análise de séries temporais, métodos causais e de redes neurais artificiais. 2014. 103f. Dissertação (Mestrado em Sistema de Informação e Gestão do Conhecimento) - Universidade FUMEC, Faculdade de Ciências Empresariais, Belo Horizonte, 2014.

1. Universidade do Estado de Santa Catarina – UDESC. E-mail: patriciabrunato@hotmail.com
2. Universidade do Estado de Santa Catarina – UDESC. E-mail: elisa.henning.@gmail.com
3. Universidade Federal de Santa Catarina – UFSC. E-mail: olgaformigoni@gmail.com

4. Universidade Federal de Santa Catarina – UFSC. E-mail: g.tortorella@ufsc.br