HOME | ÍNDICE POR TÍTULO | NORMAS PUBLICACIÓN

Espacios. Vol. 37 (Nº 31) Año 2016. Pág. 29

Fatores determinantes do preço da soja no Mato Grosso – MT

Ttermining factors in the price of soybeans in Mato Grosso-MT

José Alex do Nascimeno BENTO 1; Francisco José Silva TABOSA 2; Jair Andrade ARAUJO 3

Recibido: 08/06/16 • Aprobado: 30/06/2016

Conteúdo

1. Introdução

2. Mercado da soja e sua importância para o Brasil

3. Metodologia

4. Resultados e discussões

5. Considerações finais

Referencias

1. Introdução

No Brasil, as atividades relacionadas ao agronegócio somaram um PIB (Produto Interno Bruto) em 2013 de R$ 1,02 trilhão, alta de 3,56% em comparação com 2012 (CEPEA, 2014). Ademais, o PIB do agronegócio representará 22,8 % do PIB nacional, estimado em R$ 4,49 trilhões em 2014. Dentre as principais commodities responsáveis por este resultado encontra-se a soja, que se consolidou como a principal e mais expressiva commodity de exportação no Brasil (CEPEA, 2014).

A cadeia produtiva da soja destaca-se no agronegócio brasileiro, seja pelo valor da produção, quanto por ocupar o primeiro lugar na pauta de exportação agrícola. A soja é um produto básico para a alimentação humana, seja na forma direta, por meio do óleo vegetal ou, principalmente, como ração para a produção de carne de aves, suínos, bovinos, leite e ovos. Cabe destacar, o óleo de soja tem sido utilizado para a produção de biocombustíveis.

O complexo da soja é o segmento mais importante na pauta de exportações do Mato Grosso. Ademais, esse estado é o maior produtor de soja no Brasil, e em segundo lugar, se comparado a nível mundial, atrás apenas dos Estados Unidos. Na safra 2013/14 plantou uma área correspondente a 8.584,4 milhões de hectares, com produtividade de 3.103 kg/ha e uma produção de 26.637,4 milhões de toneladas (CONAB, 2014).  

Esse mercado tem como característica marcante sua difícil previsibilidade de preço e de produção. Tal característica surgiu de fatores que estão além do controle por parte do produtor, como variações na oferta e demanda, além das condições climáticas e enfermidades durante a produção (ABITANTE, 2008).  Além disso, pelo fato dos Estados Unidos serem os maiores produtores de soja, além de ser o mercado no qual os preços são cotados por meio da Board of Trade of the City of Chicago (CBOT), as seguintes questões tornam-se relevantes: As variações ocorridas nesse mercado afetam os demais mercados, como o brasileiro? Caso afirmativa a resposta anterior, qual a intensidade desses efeitos?

O objetivo desse estudo foi analisar os principais determinantes do preço da soja comercializada no Mato Grosso, considerando a sua quantidade produzida, as flutuações no preço da soja em grão norte-americana, a taxa de câmbio nominal, o preço comercializado da soja no Paraná e o preço dos fertilizantes. Para o desenvolvimento desse objetivo, foi utilizado o modelo de Vetores de Correção de Erros (VEC).

Além desta introdução, a seção 2 aborda o referencial teórico, a terceira seção a metodologia empregada, assim como a fonte dos dados. Os resultados são apresentados e discutidos na quarta seção e em seguida são ressaltadas às conclusões do trabalho.

2. Mercado da soja e sua importância para o Brasil

Entre os países produtores de soja em grão destacam-se os Estados Unidos, Brasil e Argentina. Da produção mundial de aproximadamente 283.788 milhões de toneladas na safra 2013/14 os três países contribuíram com 81,40% do total, tendo os Estados Unidos participado com 31,54% (89.507 milhões de toneladas), o Brasil com 30,83% (87.500 milhões de toneladas) e a Argentina com 19,03% (54.000 milhões de toneladas) (USDA, 2014).

O Brasil exportou 44.500 milhões de toneladas na safra de 2013/14, 40,22% do total de soja mundial, com os Estados Unidos exportando 39,36% e a Argentina 8,13%. Os principais fatores que explicam esse aumento do percentual brasileiro estão relacionados com a adoção de técnicas de plantio direto, além da adoção de tecnologia na produção, como por exemplo, a soja geneticamente modificada e a obtenção de menores custos na produção. A vantagem do Brasil baseia-se, sobretudo, no menor custo fixo da terra. Porém, esta vantagem pode ser perdida em virtude do aumento dos custos diretos dos fatores de produção, além das deficiências logísticas no mercado brasileiro. (CASTRO et. al, 2012).

Abordando especificamente a experiência brasileira, o país obteve um crescimento, tornando o país o segundo maior produtor mundial e o primeiro em relação as exportação. Esses números fizeram da soja em grãos o cultivo mais disseminado no país, concentrando a produção em 90% na porção centro-sul, destacando o estado de Mato Grosso como maior produtor brasileiro, com 10.523.386 de toneladas produzidas na safra 2013 (SECEX, 2014).

Com relação aos principais compradores da soja em grãos brasileira, destacam-se a China 20.712.860 milhões de toneladas (63,79% do total exportado), em seguida Países baixos com 1.001.768 milhões de toneladas (3,09%) e por fim, a Espanha com 854.299 milhões de toneladas (2,63%) (SECEX, 2014).

3. Metodologia

3.1. Base de dados

Os dados utilizados neste trabalho foram obtidos de diversas fontes. A saber: QUANT: quantidade produzida mensal de soja em grãos por tonelada no Mato Grosso. PEUA: corresponde a série de preços mensais da soja em grãos dos Estados Unidos em dólar por tonelada (US$/ton), retirada da base de dados do site United States Department of Agriculture (USDA). PMT: corresponde a série de preços mensais da soja em grãos do Mato Grosso em dólar por tonelada (US$/ton) corrigida pelo IGP-DI, com base em Dezembro/2014, obtida pelo site Agrolink. PPR: corresponde a série de preços mensais da soja em grãos do Paraná em dólar por tonelada (US$/ton) corrigida pelo IGP-DI, com base em Dezembro/2014, obtida pelo site Agrolink. TxCa: corresponde a série mensal da taxa de câmbio real em R$/US$ retirada do IPEADATA.INSUMOS: corresponde a série da média ponderada mensal referente aos preços dos fertilizantes em dólar por tonelada (US$/ton), construída da seguinte forma:

Os pesos associados (Tabela 1) aos indicadores da variável INSUMOS são oriundos de dados obtidos pelo Banco Mundial que, embora não garanta a melhor medição, permite-se a possibilidade de analisar os efeitos dos fertilizantes nas series de preço da soja estudadas (THE WORLD BANK, 2014).

Tabela 1: Pesos para cada indicador da variável INSUMOS - 2014

 Fonte: THE WORLD BANK, 2014. Elaboração dos autores.

A Tabela 2 mostra as estatísticas descritivas das séries adotadas. Observa-se que a média do preço da soja comercializada no Mato Grosso/MT (U$ 247,58) é menor do que no Paraná/PR (U$ 272,96) e nos Estados Unidos (U$ 373,34). Os insumos custam em média U$ 329,70 por tonelada. A quantidade média produzida em Mato Grosso foi de 530 toneladas.

Tabela 2: Estatísticas descritivas das séries temporais INSUMOS, PEUA, PMT, PPR e TxCa.

Fonte: Dados da pesquisa. Elaboração dos autores.

As séries estimadas para análise de relação de preços da soja no mercado do Mato Grosso foram transformadas em séries logaritmizadas, aos quais: LPMT - logaritmo natural do preço de Mato Grosso-MT; LPPR – logaritmo natural do preço do Paraná-PR. No mercado externo, considerou apenas LPEUA – logaritmo natural do preço dos Estados Unidos; LTxCa - logaritmo natural da serie estimada da taxa de câmbio; LQUANT – logaritmo natural da quantidade produzida de soja em Mato Grosso-MT  e, por fim, a LINSUMOS - logaritmo natural do preço dos fertilizantes.

3.2 Métodos analíticos

3.2.1 Teste de Raiz Unitária

Para se testar a co-integração entre as séries de preços de soja no Mato Grosso-MT, Paraná- PR e Estados Unidos, dos insumos e da taxa de câmbio, deve-se inicialmente determinar a ordem de integração. Isto é feito por meio do teste de raiz unitária. Neste trabalho empregou-se o teste de Dickey-Fuller Aumentado (ADF), que considera modelos auto-regressivos de ordem superior a um.

Nesse teste, compara-se o resultado da estatística t com os valores determinados reportados por Dickey-Fuller para determinar se aceita ou se rejeita a hipótese nula. Essa hipótese nula será rejeitada se o valor calculado da estatística t for maior do que o valor crítico de Dickey-Fuller, indicando que a série é estacionária; caso contrário a série é não-estacionária.

O teste de ADF é muito sensível à presença de valores irregulares (FERNANDES e TORO (2005). Nesse sentido, utilizou-se o teste KPSS, desenvolvido por Kwiatkowski, et.al, (1992), que sugeriram um teste cuja principal característica é permitir a mudança das hipóteses em teste, ou seja, a hipótese nula admite a noção de que a série é estacionária e, sob a hipótese alternativa, é integrada de ordem um. A vantagem desse teste resulta da falta de coerência explicativa dos testes convencionais, pois estes tendem a não rejeitar a hipótese nula com elevada frequência.

De acordo com Kwiatkowski et. al, (1992), o teste KPSS tende a complementar o teste de raiz unitária, de Dickey-Fuller. Ao testar ambas as hipóteses, de raiz unitária e de estacionariedade, podem-se distinguir séries que aparentam ser estacionárias, que simulam possuir raiz unitária e para as quais os dados (ou testes) não são suficientemente informativos para assegurar se são estacionárias ou integradas.

3.2.2 Vetores Auto-regressivos (VAR)

O modelo VAR é uma generalização para séries múltiplas do modelo auto- regressivo univariado, em que as regressões seguem à mesma estrutura para todas as equações individuais (PINDYCK e RUBINFELD, 2004).

 Neste modelo, cada variável endógena, ou dependente, é explicada por seus valores defasados das demais variáveis endógenas e exógenas presentes, embora a dicotomia endógena/exógena, fundamental para modelos estruturais, reduz muito o seu potencial em modelos auto-regressivos.

Os coeficientes estimados a partir da equação (2) não consideram as relações entre as variáveis expressas no modelo VAR. Então, o modo mais apropriado para estudar os impactos das inovações é dado pela função impulso-resposta e pela decomposição de variância (MARGARIDO, 1998).

3.2.2.1 Função de Impulso-Resposta

Uma função impulso-resposta esboça o comportamento das séries incluídas no modelo VAR, em resposta a choques ou a mudanças provocadas por variáveis residuais (ENDERS, 1995).

De acordo com o mesmo autor, os efeitos baseados na função impulso-resposta do VAR fornece um mecanismo para estimar respostas a choques, no qual ignora a pressuposição de condições, ceteris paribus, para outras variáveis do modelo.

FORMULA 29-f00

3.2.2.2 Decomposição da Variância

Segundo Enders (1995), a decomposição de variância reproduz o percentual do erro da variância prevista referente aos choques de determinada variável versus os choques nas outras variáveis do sistema. Se os choques observados numa variável z não forem capazes de explicar a variância do erro de previsão da variável y, diz-se que a sequência y é exógena. Caso contrário, diz-se que ela é endógena.

A decomposição da variância dos erros de previsão permite ver a separação da variância dos erros de previsão para cada variável em componentes que podem ser atribuídos por ela própria e pelas demais variáveis endógenas, apresentando, em termos percentuais, qual o resultado que um choque não antecipado sobre determinada variável tem sobre ela própria e sobre as demais variáveis pertencentes ao sistema (SAMPAIO et. al., 2005).

3.2.3 Vetor de Correção de Erros (VEC)

A condição necessária para que os estimadores obtidos possuam propriedades desejáveis é que as variáveis do VAR sejam estacionárias. Caso contrário, a existência de raízes unitárias deve ser levada em consideração.

Por outro lado, se a regressão utiliza-se da primeira diferença, embora elimine a possibilidade de regressões espúrias, provoca a perda de informações sobre relação de longo prazo.

Nesse sentido, para Johnston e Dinardo (1997), quando as variáveis no modelo VAR são integradas de primeira ordem ou mais, estão sujeitas às inconsistências de regressões, considerando que as variáveis sejam não–estacionárias.

Desse modo, a presença de variáveis não estacionárias, no entanto, cria a possibilidade de relações de cointegração, gerando o que é conhecido na literatura como mecanismo de correção de erros. Segundo Margarido e Barros (2000), a principal vantagem de escrever o sistema em termos de correção de erros, liga-se ao fato de que, nesse formato, são incorporadas informações tanto de curto como de longo prazo.

3.2.3.1 Testes de Co-integração de Johansen

Segundo Gujarati (2000) diz que “um teste de cointegração pode ser pensado como pré-teste para evitar situações de regressão espúria”.

A determinação correta do número de defasagens é fundamental para análise de co-integração, ou seja, o valor de p , em (8), pode ser obtido por vários métodos, entre eles, os de Akaike Information Criterion - AIC (MARGARIDO, 1998).

4. Resultados e discussões

Procurou-se, numa primeira etapa, apresentar alguns elementos que permitissem caracterizar o comportamento do referido preço ao longo do período compreendido entre janeiro de 2005 e janeiro de 2014, período para o qual há dados disponíveis. Em seguida, são apresentadas, os testes de raiz unitária (Dickey-Fuller Aumentado), teste de co-integração de Johansen, função de impulso resposta e a decomposição da variância dos resíduos para se verificar o grau de influência das relações propostas.

Os resultados obtidos a partir dos diferentes procedimentos econométricos adotados são baseados, exclusivamente, nas séries dos preços mensais da soja em grãos, nos Estados Unidos, Paraná e Mato Grosso, com o objetivo de analisar os fatores explicativos desse último, consideraram-se ainda as series mensais da taxa de câmbio, quantidade produzida e dos fertilizantes (insumos).

Para verificar a estacionaridade das séries, empregou-se o teste de Dickey-Fuller Aumentado (ADF), com resultados apresentados na Tabela 3. As estatísticas tτ, τµ, τ correspondem, respectivamente, às equações com constante e com tendência; com constante e sem tendência; e sem constante e sem tendência.

Tabela 3: Teste de Raiz Unitária, Dickey-Fuller Aumentado (ADF) para as séries de preço
logarítmizadas em nível, Janeiro de 2005 a Janeiro de 2014.

Os valores críticos para o modelo com constante e com tendência ao nível de 1%, 5%, e
10% são respectivamente -4.046072, 3.452358 e -3.151673, para o modelo com constante
e sem tendência os Valores Críticos são, ao nível de 1% (-3.492523), 5% (-2.888669) e
10% (-2.581313) e para o modelo sem constante e sem tendência os Valores Críticos são,
ao nível de 1% (-2.586753), 5% (-1.943853) e 10% (-1.614749).
***indica que a hipótese nula é rejeitada ao nível de significância de 10%.
**indica que a hipótese nula é rejeitada ao nível de significância de 5%.
*indica que a hipótese nula é rejeitada ao nível de significância de 1%.
Fonte: Dados da pesquisa, 2014. Elaboração dos autores.

Os resultados (Tabela 4) sinalizaram que todas as séries pesquisadas não são estacionárias, tendo em vista que os valores calculados são menores em módulo que seus respectivos valores críticos de 1% e 5% em todos os modelos analisados, ou seja, a hipótese nula de raiz unitária não pode ser rejeitada para estas séries consideradas.

Vale ressaltar que o teste ADF é muito sensível à presença de valores atípicos, por esta razão, fez-se necessária a estimação dos testes de raiz unitária com presença de quebras. Na Tabela 6 são apresentados os resultados dos testes de estacionariedade formulados por Kwiatkowski, Phillips, Schmidt e Shin (1992) – KPSS. Os resultados mostraram que todas as séries analisadas não são estacionárias em nível, já que a hipótese nula de estacionariedade foi rejeitada.

Tabela 4: Teste de estacionariedade formulado por Kwiatkowski-Phillips- Schmidt-Shin,
para as séries de preços logaritmizadas em níveis, janeiro de 2005 a janeiro de 2014.

Os valores críticos para o modelo com constante e com tendência são 0,2160, 0,1460 e
0,1190, a 1%, 5% e 10%, respectivamente; e para o modelo com constante e
sem tendência, 0,7390, 0,4630 e 0,3470, a 1%, 5% e 10%, respectivamente.
***indica que a hipótese nula é rejeitada a 10%.
**indica que a hipótese nula é rejeitada a 5%.
*indica que a hipótese nula é rejeitada a 1%.
Fonte: Dados da pesquisa, 2014. Elaboração dos autores.

Tabela 5
Teste de Raiz Unitária, Dickey-Fuller Aumentado (ADF) para as séries de preço
em primeira diferença logarítmizadas, janeiro de 2005 a janeiro de 2014.

Os valores críticos para o modelo com constante e com tendência ao nível de 1%, 5%, e
10% são respectivamente -4.046072,  -3.452358 e -3.151673,  para o modelo com constante
e sem tendência os Valores Críticos são, ao nível de 1% (-3.492523), 5% (-2.888669) e
10% (-2.581313) e para o modelo sem constante e sem tendência os Valores
Críticos são, ao nível de 1% (-2.586753), 5% (-1.943853) e 10% (-1.614749).
***indica que a hipótese nula é rejeitada ao nível de significância de 10%.
**indica que a hipótese nula é rejeitada ao nível de significância de 5%.
*indica que a hipótese nula é rejeitada ao nível de significância de 1%.
Fonte: Dados da pesquisa. Elaboração dos autores.

Pela razão da sensibilidade do teste ADF aumentado em primeira diferença, fez-se necessária a estimação dos testes de raiz unitária com presença de quebras. Na Tabela 6 são apresentados os resultados dos testes de estacionariedade formulados por Kwiatkowski et. al, (1992) – KPSS na primeira diferença.

Tabela 6
Teste de estacionariedade, formulado por Kwiatkowski- Phillips-Schmidt-Shin, para as séries
de preços logaritmizadas na primeira diferença, janeiro de 2005 a janeiro de 2014.

Os valores críticos para o modelo com constante e com tendência são 0,2160, 0,1460 e 0,1190,
a 1%, 5% e 10%, respectivamente; e para o modelo com constante e sem tendência,
0,7390, 0,4630 e 0,3470, a 1%, 5% e 10%, respectivamente.
***indica que a hipótese nula é rejeitada a 10%.
**indica que a hipótese nula é rejeitada a 5%.
*indica que a hipótese nula é rejeitada a 1%.
Fonte: Dados da pesquisa. Elaboração dos autores.

Todas as séries estudadas foram estacionarias com tendência e com constante e com constante e sem tendência, as séries sinalizaram rejeição da hipótese nula a 1% de significância. Os testes apontam que todas as séries analisadas foram estacionárias na primeira diferença, em ambos os modelos, o que indica que as variáveis são estacionárias nas diferenças. Dessa maneira, podem ser consideradas como integradas de ordem um.

O fato de elas serem integradas de mesma ordem constitui um pré-requisito para examinar se as séries são co-integradas, o que é identificado por meio do teste de Johansen com o intuito de verificar se elas possuem relacionamento de longo prazo.

Antes de realizar o teste de co-integração, foi necessário determinar o número de defasagens mais adequado para o modelo VAR a serem utilizadas e escolher o modelo a ser empregado. O critério de informação usado para determinação do número de defasagens foi o de Akaike (AIC). Cabe destacar, esse teste procura estimar um modelo capaz de captar uma maior quantidade de informações contidas entre as variáveis MARGARIDO (1998). Conforme o resultado do teste, a escolha do número de defasagens do modelo VAR neste trabalho levou em conta duas defasagens, pois considerou-se o critério de Akaike (-17.01841*).

Determina-se, o teste de Johansen para identificar o número de vetores de co-integração, que serão obtidos pelos testes do traço e do máximo autovalor, cujos resultados e valores críticos estão contidos na Tabela 9.   

Os resultados dos testes de co-integração, apresentados na Tabela 7, mostram que a hipótese nula de não co-integração foi rejeitada para a existência de pelo menos dois vetores de co-integração. Isso posto, será utilizado o modelo de Vetores de Correção dos Erros (VEC).

Tabela 7: Resultado do teste de co-integração de Johansen para as séries mensais: janeiro de 2005 a janeiro de 2014.

* indica rejeição da hipótese nula a 1% de significância.
** indica rejeição da hipótese nula a 5% de significância.
Fonte: Dados da pesquisa. Elaboração dos autores.

A Tabela 8 mostra o resultado do Modelo de Correção de Erros (VEC). Deve-se observar que os valores dos coeficientes estimados estão normalizados para a variável em questão (LNPMT) e que os sinais deles devem ser interpretados de forma inversa. Observa-se que todas as variáveis do modelo são estatisticamente significantes e possuem poder de explicação para o comportamento dos preços da soja do Mato Grosso no longo prazo. Podemos destacar o preço da soja dos Estados Unidos (LPEUA), onde um aumento 1% no preço da soja nesse respectivo mercado, em um período anterior, ocasiona um aumento no preço na soja do Mato Grosso em 1,15%; e se a taxa de câmbio aumentar 1%, o preço da soja do Mato Grosso aumenta 1,30%, o que indica que aumentos na taxa de câmbio proporcionam aumentos no preço da soja do Mato Grosso.  Nesses dois casos, podemos verificar que os resultados dos coeficientes são mais elásticos do que os demais. Isso mostra que, no longo prazo, o preço da soja nos Estados Unidos e a Taxa de Câmbio são os fatores que mais influenciam o preço da soja no Mato Grosso/MT.

Tabela 8: Resultado do Modelo de Correção de Erros (VEC) para o mercado do preço da soja no Mato Grosso (LPMT).

Obs: Desvio Padrão em parênteses.
Fonte: Dados da pesquisa. Elaboração dos autores.

A Tabela 9 apresenta os resultados da decomposição da variância dos erros de previsão, para cinco variáveis em uma análise de curto prazo. A primeira coluna determina a variável atribuída a um choque não antecipado, enquanto a segunda representa os períodos, no presente trabalho, expressos em semanas. Considerou-se também que um choque não antecipado sobre as variáveis analisadas perdure no máximo por 24 semanas. No caso da variável LPMT, a terceira coluna informa o percentual da variância dos erros de previsão em função de choques não antecipados sobre essa variável. As demais colunas captam percentuais das variâncias dos erros de previsão de LPMT, atribuídos às variáveis LPEUA, LPPR, LQUANT, LTxCa e LINSUMOS,.

Tabela 9: Decomposição da variância dos erros de previsão, em percentagem de LPMT, para as variáveis LINSUMOS, LPEUA, LPMT e LTXCA.

Fonte: Dados da pesquisa. Elaboração dos autores.

Os resultados da decomposição da variância dos erros de previsão de LPMT mostraram que, decorridas 24 semanas após um choque não antecipado sobre essa variável, 82,29% de seu comportamento decorreu dela própria e 17,71%, das variáveis LPEUA (12,62%), LPPR (0,32%), LQUANT (2,49%), LTxCa (2,01%) e LINSUMOS (0,24%).

Pela decomposição da variância da soja brasileira observa-se que com o decorrer dos meses aumenta a participação da soja americana na explicação das variações na soja brasileira. Esse mesmo comportamento não é verificado para o Paraná na mesma intensidadeEsse fato decorre do posicionamento do Mato Grosso na escala produtiva, sendo o primeiro maior produtor do país contra o Paraná, segundo maior produtor.

Para a função impulso-resposta também de curto prazo, a Figura 1 apresenta os resultados mostraram que o comportamento da função impulso resposta sobre o preço de Mato Grosso (LPMT) teve impacto bem definido pelo preço dos Estados Unidos (LPEUA), dado que um choque no desvio-padrão dos preços de Mato Grosso tendeu a elevar o desvio-padrão dos preços dos Estados Unidos.

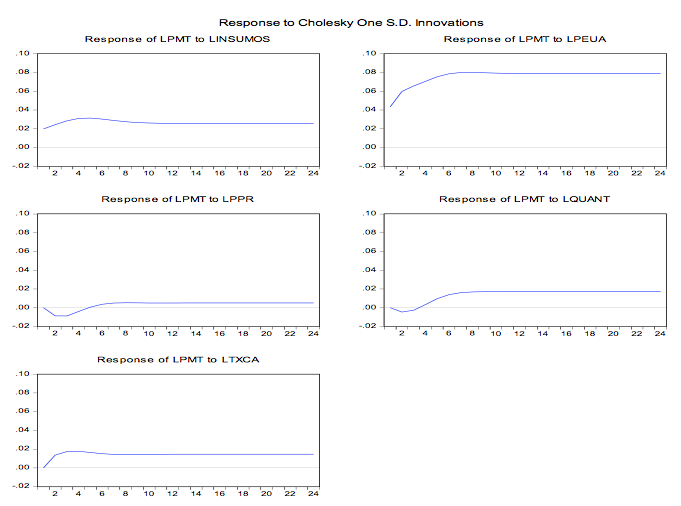
Figura 1 - Elasticidade de função de Resposta de Impulso, efeitos de choques das variáveis LINSUMOS, LPEUA, LPPR e LTxCa sobre LPMT .
Fonte: Dados da pesquisa. Elaboração dos autores.

Após a incidência desse choque no desvio-padrão do preço dos Estados Unidos, o preço no Mato Grosso aumenta e permanece no mesmo nível até o vigésimo quarto mês. Isso ocorreu porque os Estados Unidos é o maior produtor mundial, enquanto Mato Grosso, além de ser o segundo maior produtor, é atualmente o maior exportador de soja do mundo. Os preços dos insumos, a quantidade produzida e a taxa de câmbio, após um choque não antecipado sobre o desvio-padrão do preço de Mato Grosso, apresentaram comportamento semelhante, ou seja, inicialmente, notou-se elevação no desvio-padrão no nível de preços até a terceira ou quarta semana, quando atingiu o ponto máximo.

No caso das variáveis LPPR e LQUANT, observou-se que um choque no desvio-padrão nessas variáveis causou pequena queda no desvio-padrão do preço de Mato Grosso, até ao segundo/quarto mês após a incidência desse choque. Posteriormente, o desvio-padrão no preço de Mato Grosso aumenta até ao oitavo mês após o choque inicial.

O principal fator para o crescimento da cultura no País, se deve à semelhança nas condições ambientais do Centro-sul do Brasil com o que é predominante no extremo sul dos Estados Unidos, condição que favoreceu o êxito na transferência das variedades do grão bem como as implementações tecnológicas de armazenamento e produção.   Com o tempo, observa-se o surgimento de um sistema cooperativista dinâmico e eficiente no País, apoiando fortemente a produção, a industrialização e a comercialização das safras, o que gerou o estabelecimento de uma bem articulada rede de pesquisa de soja envolvendo governo e iniciativa privada. Além desses fatores citados, pode-se ainda destacar melhorias nos sistemas viário, portuário e de comunicações, que facilitam o transporte e as exportações (MELO FILHO e RICHETT, 1998). 

Sob tais melhorias, aliadas ao fato de a soja ser a maior e mais expressiva commodity no Brasil em termos de exportação (SILVA; SANTO e SILVA, 2003), as transações financeiras tornam-se relevantes para a economia do país, e decididas, desde 2008, de acordo com as negociações operadas na companhia aberta de capital brasileira BM&FBovespa, em São Paulo.  

Especificamente a respeito do mercado da soja no Brasil, a partir do momento em que a volatilidade dos preços das commodities começaram a ser balizados na Bolsa de Chicago (CBOT) e na comercialização em Rotterdam, a soja brasileira consegue consolidar sua competitividade no cenário internacional. Isso ocorre porque as cotações são transmitidas instantaneamente e sem defasagens para os preços recebidos pelos produtores no Brasil, dando ao produtor a obtenção de um “preço justo”. Além disso, a taxa de câmbio em negociação começa a funcionar como um seguro contra inflação e altas nos custos de produção (MARGARIDO e SOUSA, 1998). 

Esse tipo de balizamento deriva da tentativa de diminuir as dificuldades na previsão de preços e produção, decorrentes de fatores como: variações na oferta e demanda (necessidades e exigências da demanda dos países consumidores, além da demanda do setor alimentício animal, já que a soja é também matéria-prima na avicultura e pecuária); custos atrelados à respectiva cadeia produtiva; além das mudanças abruptas do clima e enfermidades durante a produção (MISSÃO, 2006).

5. Considerações finais

O estudo analisou os fatores determinantes do preço da soja no Mato Grosso. Os resultados de curto prazo, como a decomposição de variância, mostraram que variações no preço dos Estados Unidos têm influência considerável na formação dos preços da soja em grãos do Mato Grosso/MT, assim como a taxa de câmbio. As variáveis LPPR e LINSUMOS tiveram uma pequena participação (0,39%) e (0,24%) respectivamente, na variação dos preços da soja do Mato Grosso. As elasticidades da função de impulso-resposta mostraram que há uma longa defasagem temporal até que o equilíbrio de longo prazo seja restabelecido, isto é, os desequilíbrios transitórios são corrigidos lentamente em ambos os mercados da soja.

Verificou-se também a existência de relações de equilíbrio de longo prazo entre os preços da soja em grãos brasileira e os preços cotados nos Estados Unidos, no Paraná/PR, taxa de câmbio e aos custos com insumos. Isso implica dizer que essas variáveis são co-integradas. Mas com forte influência do preço nos Estados Unidos e pela Taxa de Câmbio.

A hipótese adotada neste estudo não foi rejeitada, uma vez que se constatou a influência bem definida do preço da soja americana no mercado de Mato Grosso.

O fato do mercado da soja ser marcado por acentuadas variações nos preços e, consequentemente, por oscilações nos rendimentos da cultura faz com que agentes que detenham informações assimétricas e maior poder de previsão sobre o comportamento do mercado captem maiores lucros.  Com essa informação os produtores e agentes econômicos tomam conhecimento do elevado risco de preço e de renda associado ao mercado da soja, tendo a possibilidade auferir lucros, mas também prejuízos conforme a dinâmica do mercado. Uma possibilidade de minimizar tais perdas e oscilações nos preços seria a utilização de contratos com mercados futuros.

Referencias

ABITANTE, K. G. Co-integração entre os mercados spot e futuro: evidências dos mercados de boi gordo e soja. Rev. Econ. Sociol. Rural, Brasília, v. 46, n. 1, p. 75-96, jan./mar. 2008.

AGROLINK. Cotações do preço da soja. Histórico de cotações. Disponível em:

http://www.agrolink.com.br/cotacoes/Historico.aspx?e=9844&p=9&l=13988. Acesso em: 21 maio. 2014.

CASTRO, L.S. de; JÚNIOR, A.G. S.; CAMPOS, A. C.;  BRAGA, M. J. Transmissão de preços e análise da volatilidade no mercado internacional da soja em grão: Uma abordagem utilizando a econometria de séries temporais. CGRCC. Instituto educacional BM&FBOVESPA, 2012. Disponível em: http://www.bmfbovespa.com.br/CGRCC/download/Transmissao-de-precos-e-analise-da-volatilidade-no-mercado-internacional-da-soja.pdf. Acesso em 28 de maio de 2014.

CEPEA - Centro de Estudo Avançados em Economia Aplicada/CNA - Confederação

Nacional da Agricultura: Produto Interno Bruto do Agronegócio – Dados de 1994 a 2013. Disponível em: <http://www.cepea.esalq.usp.br/pib/> Acesso em 28/05/2014.

CONAB - Companhia Nacional de Abastecimento. Séries Históricas. Disponível em:

http://www.conab.gov.br/OlalaCMS/uploads/arquivos/14_05_08_10_11_00_boletim_graos_maio_2014.pdf. Acesso em 20 de maio de 2014.

ENDERS, W. Applied econometric time series. New York: John Wiley and Sons, 1995.

FERNANDES, M.; TORO, J. O Mecanismo Monetário de transmissão na Economia Brasileira Pós-Plano Real. Revista Brasileira de Economia, v. 59, N. 1, p. 5-32, Jan./Mar. 2005. Disponível em: <epge.fgv.br/portal/arquivo/1293.pdf> Acesso em: 15 jun. 2006.

GUJARATI, D.N. Econometria básica. 3 ed. São Paulo: Makron Books, 2000.

HARRIS, R.I.D. Cointegration analysis in econometric modeling. London: Prentice Hall, 1995.

IPEAdata. Tema: Cambio series históricas. Taxa de cambio nominal. Disponível em: http://www.ipeadata.gov.br/ExibeSerie.aspx?serid=38389 . Acesso em 30/04/2014.

JOHANSEN, S.; JUSELIUS, K. Maximum Likelihood estimation and inference on cointegration with applications to the demand for money. Oxford Bulletin of Economics and Statistics, V. 52, N. 2, p. 169-210, 1990.

JOHNSTON, J.; DINARDO, J. Econometric Methods. 4 ed. Singapore: McGraw-Hill. 1997.

KWIATKOWSKI, D.; PHILLIPS, P.C.B.; SCHMIDT, P.; SHIN, Y. Testing the null hypothesis of stationarity against the alternative of a unit root. How sure are we that economic time series have a unit root? North- Holland: Journal of Econometrics, V. 54, p. 159-178. 1992.

MARGARIDO, M.A. Transmissão de preços internacionais de suco de laranja para preços ao nível de produtor de laranja no Estado de São Paulo. Instituto de Economia Agrícola. Coleção Estudos Agrícolas 6. São Paulo-SP. 1998.

MARGARIDO, M. A.; SOUZA, E. L. L. Formação de preços da soja no Brasil. Agricultura em São Paulo, São Paulo, v. 45, n. 2, p. 52-61, 1998.

_______. BARROS, G.S.C. Transmissão de preços agrícolas internacionais para preços agrícolas domésticos no Brasil. Agricultura,. São Paulo-SP, V. 47, N. 2, p. 53-81. 2000.

MDIC (Ministério do desenvolvimento, indústria e comércio exterior); SECEX (Secretaria do comércio exterior). Balança Comercial. Brasil, Grandes Regiões e Unidades da Federação. 2014.

MELO FILHO, G. A. de; RICHETTI, A. Perfil socioeconômico e tecnológico dos produtores de soja e milho de Mato Grosso do Sul. Dourados: Embrapa-CPAO, 1998. 57 p. (Documentos, 15).

MISSÃO, M. R. Soja: origem, classificação, utilização e uma visão abrangente do mercado. Maringá Management: Revista de Ciências Empresariais, Maringá, v. 3, n. 1, p. 7-15, jan./jun. 2006.

PATTERSON, K.D. An Introduction to Applied Econometrics: a time series approach. Great Britain: St. Martin´s Press. 2000.

PINDYCK, R.S.; RUBINFELD, D.L. Econometria: Modelos e previsões. 4 ed. Rio de Janeiro: Ed. Campos. 2004. 

SILVA, W. V.; SANTO, E. L.; SILVA, L. S. C. Co-integração entre os preços da soja cotados nos mercados brasileiro e norte-americano: uma análise empírica. Caderno de Pesquisas em Administração, São Paulo, v. 10, n. 3, p. 69- 78, jul/set 2003.

THE WORLD BANK. World Bank Commodity Price Data (The Pink Sheet). Disponível em:http://siteresources.worldbank.org/INTPROSPECTS/Resources/334934-1304428586133/pink_data_m.xlsx. Acesso em 1 de maio de 2014.

USDA- United States Department of Agriculture. Foreign Agricultural Service. Oilseeds:World markets and trade. Disponível em: <http://www.fas.usda.gov/psdonline/circulars/oilseeds.pdf>. Acessado em: 26/05/2014

1. Mestre em Economia Rural (UFC). E-mail: josealex18@yahoo.com.br
2. Doutor em Economia, Professor do Curso de Mestrado em Economia Rural/MAER da Universidade Federal do Ceará (UFC). E-mail: franze@caen.ufc.br
3. Doutor em Economia, Professor do Curso de Mestrado em Economia Rural/MAER da Universidade Federal do Ceará (UFC). Fone: (85) 33669716. E-mail: jaraujoce@gmail.com