HOME | ÍNDICE POR TÍTULO | NORMAS PUBLICACIÓN

Espacios. Vol. 37 (Nº 28) Año 2016. Pág. 8

Convergência de preços intrarregionais: Uma análise dos produtos hortifrutigranjeiros no Brasil

Price convergence intra regional: An analysis of horticultural products in Brazil

Gerrio dos Santos BARBOSA 1; Francisco José Silva TABOSA 2; Jair Andrade ARAUJO 3

Recibido: 18/05/16 • Aprobado: 15/06/2016

Conteúdo

1. Introdução

2. Convergência dos preços de produtos agropecuários

3. Metodologia

4. Resultados e discussões

5. Considerações finais

Referências

1. Introdução

O mercado de produtos agropecuários tem forte relevância no contexto socioeconômico mundial. Pesquisadores e formadores de políticas estão receosos quanto à oferta de alimentos, em razão da elevada densidade populacional do planeta. Para tanto, faz-se necessário um aumento produtivo e logístico na distribuição dos alimentos, fornecendo menores preços aos bens essenciais para o consumo. Nessa perspectiva, é importante pesquisar a convergência de preços dos hortifrútis entre os mercados brasileiros. Segundo Barrett (2001), a abordagem de convergência é uma relevante ferramenta na transmissão de políticas macroeconômicas na análise de mercados nacionais e/ou internacionais, que surgem de unidades microeconômicas e possibilitam o crescimento econômico por meio das inovações tecnológicas. Diante disso, as integrações dos mercados internos surgem da interdependência entre os preços dos diversos mercados.

No Brasil, alguns estudos empíricos mostram, na maioria das vezes, a convergência dos preços entre mercados e suas relações com o crescimento em longos períodos, como por exemplo, Mayorga et al. (2007); Mayorga et al. (2009); Figueiredo et al. (2010); Aguiar e Figueiredo (2011); Soares et al. (2012); Figueiredo, Souza-Filho e Paullilo(2013); Tabosa, Irffi e Penna(2014); Tabosa et al. (2014). Na literatura internacional, destacam-se os recentes estudos realizados por Dreger et al. (2007); Cioffi, Gaetano e Damiano(2011); Lindenblatt e Feuerstein (2015) e García-Hiernaux, Guerrero e Mcaleer(2015). 

O presente estudo examina a validação da Lei do Preço Único (LPU) para os mercados hortifrutigranjeiros no Brasil. Desta forma, questiona-se a existência de convergência no longo prazo para os produtos analisados. Estas indagações serão testadas pelos exercícios de convergência absoluta. De acordo com a teoria predita, os mercados de competição perfeita que não se encontram custos de transportes, informações assimétricas, barreiras comerciais (por exemplo, tarifas) e produtos semelhantes negociados em locais diferentes devem ser vendidos por preço único quando estes são expressos na mesma moeda. Portanto, ao analisar mercados sob mesma legislação, pode-se afirmar que estes são homogêneos.

Conforme a literatura, os testes de β e σ convergência são extensivamente realizados na forma absoluta e condicional. Na forma absoluta, os mercados devem ser homogêneos, convergindo para estados estacionários idênticos. No aspecto condicional, a convergência é atenuada as características dos indivíduos como fatores econômicos, institucionais, tecnológicos, entre outros, que proporcionam o alcance de múltiplos estados estacionários.

No contexto metodologico, destacam-se: Friedman (1992); Barro e Sala-I-Martin (1991, 1992); Islam (2003); Dobado e Marrero (2005); Dreger et al. (2007); Wolszczak-Derlacz (2008); Pfaffermayr (2009); Egger e Pfaffermayr (2009) e Lindenblatt e Feuerstein (2015). Eles explicavam que, para testar a convergência é necessário apresentar-se reversão à média por meio do β-convergência, caso contrário, deve-se investigar o σ-convergência, ou seja, se de fato a variação dimininui entre dois pontos no tempo. No Brasil, estudos realizados por Spohr e Freitas (2011) e Penna e Linhares (2013a; 2013b) analisaram essas técnicas e suas controvérsias, direcionadas para o PIB agropecuário per capita brasileiro.

O objetivo deste trabalho é determinar a existência da convergência de preços nos 37 produtos para os 16 centros analisados no Brasil. Os métodos utilizados foram testes de raízes unitárias para dados em painel β e σ convergência absoluta, que examinam a LPU. Consoante, a foram testadas testam-se taxas de crescimento dos preços (β-convergência) e sua dispersão (σ-convergência) no tempo. A contribuição empiríca do esboço situa-se na compreensão do comportamento dos preços em longos períodos para mercados ditribuidores de hortifrutigranjeiro, observada a validação ou violação da Lei do Preço Único. Ressalta-se que não há na literatura nacional estudos usando as metodologias β e σ convergência para os produtos hortifrutigrajeiros, além da quantidade de mercadorias analisadas.

O presente artigo será composto por esta introdução e mais cinco seções. A segunda seção mostrará breve revisão da literatura sobre a convergência dos mercados atacadistas de produtos agropecuários. A terceira discorrerá sobre a fonte dos dados, estatística descritiva e os metodos econométricos aplicados. Na quarta seção, serão apresentadas as discussões dos resulatados estimados de β e σ convergência. Já a seção quinta é dedicada às considerações finais.  

2. Convergência dos preços de produtos agropecuários 

O estudo de Hotelling (1929) é apontado em Bukenya e Labys (2005) e Tabosa Irffi e Penna(2014) como pioneiros nas pesquisas de concorrência imperfeita e das teorias espaciais sobre discriminações dos preços. Os processos de arbitragem dos preços espaciais formalizaram-se no equilibrio em mais de dois mercados, segundo Enke (1951) e Samuelson (1952). Assim, as dispersões espaciais dos preços estavam intrinsicamente relacionadas às teorias do comércio internacional.  

Samuelson (1952) utilizou o princípio de Heckscher-Ohlin para elaborar o problema de equalização de preços dos fatores. Destarte, um nível crescente de integrações dos mercados são condições essenciais para a livre mobilidade dos fatores de produção. Mattos et al. (2009) explicaram que, não havia um concenso entre os pesquisadores na apreciação de um conceito único sobre “integração de mercado”. Enquanto Mayorga (2007) explanou que os primeiros estudos sobre transmissão de preços e integrações dos mercados utilizavam análises de correlações e regressões simples, que conferem um caráter estático às análises.

No Brasil, Silva e Margarido (2009) mostraram que, as elasticidades de transmissão de preços nos mercados da mandioca nos estados de São Paulo e Paraná apresentaram integração no longo prazo, que valida a LPU. Desse modo, o mecanismo de arbitragem funcionava para os dois mercados observados.

Os mercados de algodão brasileiro e estrangeiro foram explorados por Sousa e Campo (2009), que concluíram relação de integração dos preços médios no longo prazo, tanto para o mercado interno como externo. No entanto, rejeitou-se a hipótese de perfeita integração dos mercados, que transgrediu a LPU para o setor algodoeiro nessa amostra.

Mattos et al. (2009) abordaram a integração no mercado de boi gordo entre os estados de São Paulo e Minas Gerais. Utilizaram o método threshold sem testarem as quantidades de regimes para os ajustes nos preços. Da mesma forma, foram pesquisados diferentes mercados regionais do frango no Brasil, no período de Janeiro de 1998 a Junho de 2007. Os autores empregaram as técnicas de cointegração threshold com determinação do número de regimes estatisticamente indicados para diferentes mercados regionais. Os resultados mostraram que os modelos com dois regimes se ajustaram melhor para um grupo de mercados, enquanto para os demais mercados, os melhores ajustes foram os modelos com três regimes. Com relação aos custos de transação, recorreram às técnicas de maior relevância, tendo em vista, que foram quase sempre negligenciados, sendo responsáveis por reconhecerem as influências destes custos sobre as ligações econômicas nos mercados espacialmente separados.

Com intuito de analisar a transmissão de preços entre os exportadores de amêndoa da castanha do caju e produtores de castanha de caju em casca no Brasil, no período de agosto de 1998 a agosto de 2008, Figueiredo et al. (2010) testaram as causalidades e estimaram as elasticidades de transmissão de preços. Os resultados indicaram causalidades de preços dos exportadores nos preços recebidos pelos produtores, no entanto, não apresentaram causalidades dos preços dos produtores com influência nos preços exportados de castanha. Por fim, as elasticidades demostraram uma transmissão de 26,7%, tanto para elevações, quanto para baixas de preços.

De forma semelhante, Adami e Miranda (2011) avaliaram a dinâmica de formação de preços do arroz nos estados do Rio Grande do Sul (RS) e Mato Grosso (MT), no período entre agosto/1999 a junho/2010. Os testes de causalidades de Granger indicaram que os preços do RS foram importantes nas previsões de preços do MT. Estimaram o modelo de transferência de correção dos erros para MT, que respondeu aos seguintes impactos: para cada 1% de aumento na taxa de crescimento dos preços no RS, essa mesma taxa em MT tinha, em média, um aumento de 0,44% no período contemporâneo e 0,17% com um período de defasagem. Concluíram que, ao elevar as taxas de crescimento dos preços no RS, os preços no MT eram sentidos no período atual e em menor magnitude no período posterior.

No estado de São Paulo, Aguiar e Figueiredo (2011) utilizaram preços médios mensais aos produtores, no atacado e varejo, de 1989 a novembro de 2008, exceto para o feijão, que iniciou em abril de 1993. As mercadorias analisadas foram o arroz, feijão, carne bovina, carne suína, carne de frango, ovos, queijo minas e óleo de soja. O teste de causalidade apontou para fortes participações dos produtores do atacado na formação de preços, que decorreram das características estruturais do mercado e do elevado nível de especialização, pois os atacadistas operavam apenas um tipo de produto e, assim, absorviam mais informações que os produtores e varejistas.

Tabosa, Ferreira e Castelar (2014) exploraram os modelos de convergência para LPU, nos mercados sem custos de transação versus aqueles com custos de transação, para os mercados atacadistas de tomate brasileiro. Os resultados atestaram que os custos são significantes, assim, evidenciou-se um processo de integração entre mercados atacadistas de tomate com custos de transação.

A LPU foi examinada em 45 produtos de 13 países da região do euro, de 2008 a 2012. Kulikov (2014) utilizou preços desagregados de Nielsen baseados em regressões log-linear não estrutural com efeitos espaciais, com utilização do método bayesiano. Após estimação dos dados, sugeriu-se forte interdependência dos preços relativos, nos espaços geográficos e dimensões de vários produtos. Por fim, considerou que um nível de renda relativa e um forte crescimento econômico afetariam os preços dos produtos amostrados.

A convergência dos preços nos mercados europeus foi observada por Lindenblatt e Feuerstein (2015), após serem incorporados os novos membros à União Europeia, em 2004. Foi o primeiro estudo sobre convergência visando o preço de varejo de mais de 400 produtos a um nível desagregado, para os velhos membros (EU15) e para os novos membros da Europa Central e Oriental (EU8). Os autores aplicaram ainda o método σ-convergência de Egger e Pfaffermayr (2009), sendo que os resultados apresentaram divergências nos preços em todos os períodos que antecederam as adesões de novos membros na União Europeia, no entanto, tais preços, convergiram em anos posteriores às adesões. Com a decomposição das variações dos preços, asseguraram que havia um processo de convergência dentro da União Europeia, impulsionado pelas dinâmicas da EU8. O efeito principal é a convergência da EU8 e EU15.

Kim e Ryu (2015) investigaram velocidade de convergência nos países desenvolvidos (G7). Aplicaram modelos estocásticos não paramétricos e não lineares, de dezembro de 1969 a fevereiro de 2015. Adotaram as seguintes noções estatísticas: memória curta na média (short memory in mean-SMM) e memória curta na distribuição (short memory in distribuition-SMD). Os resultados apontaram evidências de convergência dos preços das ações na França, Alemanha, Reino Unido e Estados Unidos. Já Canadá, Itália e Japão resultaram em evidências limitadas de convergência.

Lindenblatt e Feuerstein (2015) captaram disparidades de preços de produtos similares no mercado único da Europa, anterior à adesão (2001-2013), que justificaram pelas diferenças nos custos e/ou correspondentes às alterações nos preços globais, os quais deveriam diminuir em longos períodos de tempo, conforme as integrações contínuas dos mercados elevassem a convergência dos preços.

Em perspectiva histórica, García-Hiernaux, Guerrero e Mcaleer (2015) desenvolveram modelos para o mercado de preço nominal, que eram equivalentes entre a LPU, mercado integrado e preço de convergência em distribuição. Chegaram os autores a duas conclusões: a primeira apontou para o mercado de grãos doméstico nos EUA, o qual foi mais integrado no século XIX. Em segundo lugar, a união europeia alcançou taxas de convergências no longo prazo, no entanto, fracassou em sua convergência na média, variância e distribuição.  

3. Metodologia

3.1. Testes de Raiz Unitária para Dados em Painel

O modelo que analisa o teste de raiz unitária pressupõe que os dados são indenpendentes e identicamente distribuídos (i.i.d). Essa abordagem pode ser observada de forma detalhada nos estudos de Quah (1994), Maddala e Wu (1999), Levin, Lin e Shu (2002) e Im, Pesaram e Shin (2003).

Em geral, os testes aparecem conforme segue a expressão:

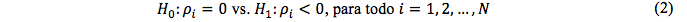
No presente estudo, os testes que investigam a existência ou não de raiz unitária (não-estacionariedade) são Levin-Lin-Chu, Im-Pesaram-Shin e Fisher-Type.

3.2. β-convergência e σ-convergência

Uma questão central em torno da qual a literatura recente do crescimento tem evoluído é o estudo de convergência. Neste, busca-se compreender se os níveis de preços nos mercados convergem para um preço médio único. No determinado contexto, Islam (2003) explicou que, quando as regiões são do mesmo país, supõe-se estado estacionário idêntico nas unidades da federação. Desta forma, a convergência absoluta apresenta-se com maior robustez. 

O conceito de β-convergência refere-se à reversão à média, postulando em sua forma absoluta, que regiões pobres (com baixa renda ou baixa produtividade) experimentarão um crescimento de renda ou produtividade mais rápida. Assim, mercados com menores preços convergem em longos períodos para alcançarem os níveis de preços superiores dos outros mercados. Por outro lado, a forma condicional, afirma que economias parecem convergir para seu próprio estado estacionário determinadas por suas idiossincrasias.

O σ-convergência implica na redução da variância dos níveis de preços, examinados nas séries temporais. Na mesma perspectiva, β-convergência mede a locomoção dos mercados dentro da distribuição, que investiga a convergência de estruturas com menores preços para aquelas com preços elevados. Portanto, o estudo avalia uma contração na disparidade entre os preços dos produtos, nos diversos mercados de distribuição de produtos hortifrutigranjeiros.  Barro e Sala-I-Martin (1995) evidenciaram que ambos os conceitos revelam a Lei do Preço Único em condições de longo prazo.

Penna e Linhares (2013b) explicaram as controvérsias na abordagem de convergência com relação às análises de séries temporais e cross-section. A análise cross-section tem como fundamentação a hipótese de β-convergência, enquanto a série temporal apresenta análise de σ-convergência. Contudo, o modelo que será examinado na estimação de convergência para os preços de produtos agropecuários exibe uma combinação de corte transversal e séries de tempo. Portanto, podem ser aplicados os dois conceitos supramencionados.

Nesta análise, β-convergência absoluto é construído sobre uma relação negativa entre o nível de preço inicial e o aumento do preço subsequente. Desta forma, o nível de preço inicial será usado para explicar mudanças subsequentes nas medidas dos preços, utilizando uma estimação em primeira diferença, com o preço em logaritmo natural. Nesse contexto, o modelo é estimado similarmente a Dobado e Marrero (2005); Dreger et al. (2007); Wolszczak-Derlacz (2008) e Lindenblatt e Feuerstein (2015):

Em particular, revelam-se dois parâmetros dos resultados das regressões, a velocidade de convergência e o Half-life, respectivamente:

No caso de grandes ordens autorregressivas, o valor absoluto do coeficiente de primeira ordem é uma aproximação apropriada para obter medidas para velocidade de convergência e o half-life. De acordo com a estrutura da regressão do modelo, é possível a presença de heterocedasticidade e autocorrelação. Dessa forma, utiliza-se o método de Generalized Least Squares (GLS), que possibilita a correção dos estimadores, de forma a encontrar variância mínima e não viés nos coeficientes.

O método σ-convergência é testado conforme expressão:

3.3. Base de Dados

Os dados utilizados foram extraídos do Programa Brasileiro de Modernização do Mercado Hortigranjeiro (PROHORT), da Companhia Nacional de Abastecimento (CONAB). As séries usadas são de preços médios mensais de 16 mercados atacadistas de alimentos do Brasil, no período compreendido entre janeiro de 2007 a julho de 2015, perfazendo um total de 37 produtos e 1.648 observações por mercadoria. Os preços nominais foram deflacionados pelo Índice Geral de Preços-Disponibilidade Interna (IGP-DI), retirado na plataforma do Instituto de Pesquisa Econômica Aplicada (IPEADATA), utilizando-se como mês base, julho de 2015. Os mercados analisados são Belém (PA), Belo Horizonte (MG), Campo Grande (MS), Curitiba (PR), Florianópolis (SC), Fortaleza (CE), Natal (RN), Porto Alegre (RS), Recife (PE), Rio de Janeiro (RJ), Salvador (BA), São Paulo (SP), João Pessoa (PB), Sorocaba (SP), Uberaba (MG), Vitoria (ES). Adiante, aplicou-se, o logaritmo natural nas séries de preços para cada produto. Os valores são expressos em reais por dezena (R$/Dz) para a alface e os ovos, reais por unidade (R$/Un) para o abacaxi, coco verde e couve-flor, e os demais alimentos em reais por quilo (R$/Kg).

Antes de examinar as regressões estimadas, exploram-se as estatísticas descritivas em relação às variações dos diferentes preços e suas médias absolutas.

Da análise da Tabela 1, verifica-se a descrição dos mercados de alimentos atacadistas do Brasil para 37 produtos observados. Os produtos que se destacam com maiores preços médios nas distribuidoras brasileiras são: o morango, a alface, a pera-estrangeira e a uva-itália, que custam em média, R$ 9,42, R$ 8,54, R$ 4,96 e R$ 4,31, respectivamente. Suas medidas foram avaliadas em quilogramas, exceto a alface, que é vendida em dezenas. Destarte, mostram-se com menores preços: a melancia, R$ 0,90, o repolho, R$ 0,99 e a laranja-pera, R$ 1,03, por quilograma. Ademais, ao analisar o desvio padrão, o morango varia, em média, 5,71 R$/Kg, enquanto a melancia possui menor dispersão no período observado e varia 31 centavos por quilograma.

Pode-se observar ainda as disparidades de preços de alguns produtos no período. Os produtos cujos valores apresentaram discrepâncias de preços são: o morango, com mínimo de R$ 1,18 e preço máximo de R$ 98,09; a alface com mínimo de 0,39 e máximo de R$ 31,76 e a mandioca-aipim que oscila de 35 centavos a R$ 26,75. A variabilidade destes é grande, talvez, devido à sensibilidade na produção de hortícolas, que podem ser afetadas por fatores externos aos produtores, como estiagens, excesso de chuvas, etc., o que reduz a oferta. Ou ainda, pelo fato de alguns mercados estarem localizados em regiões que produzem determinados produtos em pequena escala e necessitam importar das regiões produtoras. Desse modo, os custos ficam elevados e, na maioria das vezes, repassados para os consumidores.

Tabela 1. Estatística Descritiva dos Preços no Mercado Atacadista de Alimentos no Brasil.

Fonte: Base de Dados. Elaboração dos autores.

Adicionalmente, com objetivo de enriquecer o exercício, apresenta-se na Tabela 1A (Anexo) uma comparação dos preços médios para as regiões Nordeste, Sudeste e Sul. Neste esboço, os preços são referentes a cada produto para cada região brasileira mencionada. Em um contexto geral, reporta-se que os produtos com menores preços por região são:

• Nordeste: abacaxi, banana-prata, coco-verde, goiaba, laranja-pera, limão-taiti, mamão-havaí, manga, maracujá-azedo, melancia, melão-amarelo, tomate e uva-itália.
• Sudeste: abacate, abóbora, berinjela, cenoura, jiló, mandioca-aipim, morango, ovo, pepino, pimentão-verde e quiabo.
• Sul: abobrinha, alface, batata, batata-doce, beterraba, cebola, couve, couve-flor, chuchu, maçã nacional, pera-estrangeira, repolho e vargem.

Nesta perspectiva, as descrições estatísticas examinam preços menores de algumas culturas produzidas em uma região comparada às demais. Provavelmente estes produtos com menores preços em determinadas regiões apresentam seu cultivo em larga escala, por isso, os mercados que se encontram próximos podem ser beneficiados com a redução dos custos (por exemplo, transportes, subsídio governamental, mão-de-obra barata, entre outros).

Em suma, o sumário descritivo não infere ou afirma a LPU dos mercados em análise. Para tanto, na seção seguinte serão estimados os testes de raízes unitárias e regressões de β-convergência e σ-convergência.

4. Resultados e discussões

Inicialmente, aplicou-se o procedimento Levin-Lin-Chu, Im-Pesaram-Shin e Fisher-Type, para testar a hipótese de raiz unitária, para cada um dos 37 produtos nos 16 mercados. 

Na Tabela 2A, que se encontra no anexo, são mostrados os resultados das estatísticas dos testes de raízes unitárias para dados em painel, que apresentam estacionariedade em nível dos preços para todos os produtos observados, aos níveis estatísticos de 5%. Portanto, sugere-se que há o processo de convergência dos preços nos mercados atacadistas brasileiros de hortifrutigranjeiros para cada produto.

No que concerne à estimação de β-convergência, primeiro, estimou-se os modelos de efeitos fixos contra o pooling, por meio da estatística F, sendo a hipótese nula de pooling rejeitada ao nível de significância de 1%. Consoante, testou-se a hipótese nula de efeitos aleatórios contra a alternativa de efeitos fixos, por meio do teste de Hausman, que resultou na rejeição de modelos com efeitos aleatórios. Ademais, testou-se no modelo de efeitos fixos a presença de heterocedasticidade e autocorrelação, que estatísticamente foram confirmadas. O problema exige a utilização do método de correção GLS, que obtêm coeficientes não viesados e possuem variância mínima.

Ao analisar a Tabela 2, observa-se o comportamento dos preços de cada produto para os 16 mercados atacadistas de hortifrútis. Estes indicam que todos os produtos observados possuem um coefciente angular negativo, de acordo com o predito na teoria e suas razões t significativas em termos estatísticos ao nível de 1%. Diante do exposto, pode-se afirmar que nos 16 mercados analisados, existem fortes indícios de β-convergência absoluta. Portanto, os mercados atacadistas convergem para um mesmo estado estacionário, o que valida a Lei do Preço Único. Desta forma, os resulatdos das regressões indicam relação inversa entre a variável dependente (taxa de crescimento dos preços do período  em relação ao ano base) e a independente (logaritmo natural do preço no ano base, ), assim, um aumento no preço do ano base reduz a diferença na taxa de cresimento dos preços.

Com relação à taxa de convergência (ou velocidade de convergência), , esta foi construída a partir do coeficiente , aplicando-se a equação (5). De forma similar, usando o valor da velocidade de convergência, na equação (6), computou-se o valor da half-life, . Na tabela 2, pode-se analisar resumidamente os produtos que se ajustam de forma rápida entre os 16 mercados analisados e, da mesma forma, aqueles cujo ajuste ocorre lentamente.

Tabela 2. Estimação do GLS para β-convergência, velocidade de convergência e half-life.

Fonte: Elaboração dos autores. * Significantes ao nível de 1%. As estatísticas t
do β-convergência podem ser solicitadas aos autores via emails.

Na Tabela 3, nota-se velocidade de convregência lenta nos cinco primeiros produtos, enquanto os cinco últimos apresentam velocidades vertiginosas. Verifica-se o coco verde com  e significa que, em média mensal, a taxa de crescimento do preço converge para um determinado estado estacionário, perfazendo 2,96%. Explica-se que uma pequena velocidade de convergência levará o half-life a um valor maior, implicando que, quanto menor a velocidade de um preço convergir, maior será o tempo necessário para reduzir à metade da distância que separam mercados com menores preços dos que possuem preços elevados. Portanto, o coco verde converge de forma lenta para um preço médio único, necessitando de 23 meses para alcançar o equilíbrio nos mercados atacadistas de hortifrútis.

Por outro lado, o chuchu possui elevada velocidade de convergência, ou seja, resulta em . Assim, o preço converge para o equilibrio em média mensal de 28,62%, que implica em um menor half-life. Mantendo-se as condições atuais, é necessário, em média, de dois meses para que alcancem o equilibrio dos preços praticados nas centrais de abastecimentos.

Tabela 3. Ranking dos cinco produtos com menores e maiores velocidades de convergência.

Fonte: Elaboração dos autores.

O coco verde, banana-prata, abacaxi e goiaba são avaliados com menores velocidades de convergência. A produção frutícola é intensiva no Nordeste brasileiro, por isso originam menores discrepâncias nos preços destes produtos, conforme apresenta a Tabela 1A (Anexo). Nesse contexto, a menor velocidade de convergência pode decorrer do volume de exportações realizadas. Dessa forma, os preços nos mercados domésticos, possivelmente, podem não estarem sendo afetados pelos demais mercados.

Em relação às maiores velocidades de convergência, aparecem o chuchu, pepino e pimentão-verde, que mostram menores preços no Sudeste do Brasil, indicando a região como sua principal produtora. A provável justificativa ocorre pelo fato da CEAGESP (estado de São Paulo) ser a maior central de abastecimento hortifrúti. Adicionalmente, essa região possui tecnologias agropecuárias modernas e rapidez na velocidade de informações. Mayorga et al. (2007) e Tabosa, Ferreira e Castelar (2014), analisaram as distribuiodoras de melão e tomate nos mercados brasileiros, respectivamente. Encontraram indícios de que a CEAGESP influencia todos os mercados do país e desponta como maior intermediadora nacional. Dessa forma, os choques em outros mercados não afetam os preços na CEAGESP, portanto, a velocidade de informações na região exerce um poder de barganha sobre mercados de outras regiões.

Em suma, menores velocidades de convergência alcançam elevados half-lifes. Assim, os produtos convergem lentamente para o estado estacionário. De forma contrária, convergem rapidamente quando se apresentam maiores velocidades.

Em termos gerais, a β-convergência é constatada nos preços dos produtos de todos os mercados analisados, indicando os produtos que apresentam velocidades elevadas no processo de convergência e os que apresentam reduzida velocidade. Já na Tabela 4, o σ-convergência apresenta seus resultados no mercado de alimentos, o que mostra a tendência de convergência ao longo dos meses analisados.

Tabela 4. Estimação do σ-convergência.

Fonte: Elaboração dos autores. * Significantes ao nível de 1%. As estatísticas t do σ-convergênciapodem ser solicitadas aos autores via emails.

Estimando σ-convergência, utilizou-se processo semelhante ao de β-convergência mencionado anteriormente. Conforme a Tabela 5, todas as estimativas são significantes em nível estatístico de 1%. Os resultados indicaram que a beterraba, laranja-pera, melão-amarelo e pera-estrangeira são produtos cujas disperssões dos preços, ao longo dos anos analisados, não violam o processo de σ-convergência. Contudo, este processo ocorre de forma lenta, tendo em vista que os coeficientes se aproximam de zero.

Quanto aos coeficentes positivos, que contradizem o conceito de σ-convergência, estes apresentam valores pequenos, sugerindo que o aumento da dispersão no tempo não acontece de forma elevada. Os resultados apontam para violação da definição de σ-convergência na maioria dos produtos. Isto decorre, provavelmente, devido às diferentes taxas de crescimento mensais de preços nos diferentes mercados analisados, mantendo, assim, um elevado grau de variação dessa taxa de crescimento e a manutenção ao longo dos meses, ou mesmo pelo fato destes possuirem diferentes tecnologias e/ou capital humano. Da mesma forma, os centros em análise podem diferir na infraestrutura, velocidade de informações e nos custos de transportes, impossibilitando rapidez e eficiência na distribuição das mercadorias. Por fim, as mercadorias hortifrutigranjeiras tem enorme grau de perecibilidade, o que agrava a logística de transporte e  tramites legais, como. por exemplo, a certificação no padrão de qualidade dos produtos. Portanto, apresentam incertezas em sua volatilidade, que pode ser um fator preponderante na redução ou elevação abrupta da dispersão dos preços em longo prazo.

5. Considerações finais

Neste estudo foram realizados testes de convergência absoluta das taxas de crescimento dos preços médios retirados das centrais distribuidoras de alimentos, verificando a validade ou violação da Lei do Preço Único em longo prazo. Nesta perspectiva, foram utilizados testes de raízes unitárias nos dados de preços mensais de 37 produtos em 16 mercados brasileiros, de janeiro de 2007 a julho de 2015. Dessa mesma forma, foram regredidos 37 modelos de β e σ-convergência absoluta.

Os testes de estacionariedades resultaram na rejeição da hipótese nula de raiz unitária, em termos significativos, para todos os produtos analisados. Com isso, sugere-se a ocorrência do processo de convergência dos preços atacadistas no Brasil. Similarmente, as estimativas dos modelos β-convergência absoluta evidenciaram sinais negativos nos coeficentes β’s, nos produtos analisados, conforme previsto na literatura. Dessa forma, os parâmetros fornecem estimativas significantes em níveis de 1%, indicando, empiricamente, que os preços de cada produto nos 16 mercados convergem para um estado estacionário. Portanto, é validada a Lei do Preço Único para os mercados atacadistas brasileiros de hortifrutigrangeiro.

Por meio do β-convergência, calculou-se a velocidade de convergência e o half-life dos preços das mercadorias. Constatou-se menor velocidade no abacaxi, na banana-prata e na goiaba. Por outro lado, o chuchu, pepino e pimentão-verde convergem com maior velocidade para um preço médio único. De forma semelhante, o half-life resulta em quantos meses um mercado leva para atingir metade da distância em relação aos preços dos mercados no estado estacionário. O coco verde, em média, necessita de 23 meses para convergir para o preço de equilíbrio. Já o chuchu alcança seu preço de equilíbrio, em média, em dois meses.

A hipótese de σ-convergência foi violada em relação a 33 produtos analisados. Com isso, constata-se que a dispersão dos preços dos produtos eleva-se ao longo do tempo. Foram apresentados nas estimações os coeficientes positivos, entretanto, com pequena magnitude. Da mesma forma, quanto aos quatro produtos cujo processo de σ-convergência ocorre, mostraram-se pequenos impactos do coeficiente temporal na variável dependente, ou seja, na dispersão.

Por último, o β-convergência foi comprovado, mas a hipótese de σ-convergência foi violada em 33 produtos, dos 37 analisados. Portanto, recomenda-se para os próximos estudos a utilização dos testes de convergência condicionais e/ou clubes de convergência, tendo em vista que esta modelagem pode levar a múltiplos estados estacionários, devido às idiossicrasias em cada mercado, como os custos de tranportes e/ou a logística empregada no setor. Deste modo, são necessárias políticas públicas que reduzam os custos de transações e logísticos, adequando e criando novas alternativas de transportes para que as distribuidoras de alimentos possam circular com mais agilidade e possibilitar, por exemplo, maior aquisição pelos pequenos compradores. 

Referências

ADAMI, A. C. O.; MIRANDA, S. H. G. de. Transmissão de preços e cointegração no mercado brasileiro de arroz. Rev. Econ. Sociol. Rural, v. 49, n. 1, p. 55-80, 2011.

AGUIAR, D. R. D.; FIGUEIREDO, A. M. Poder de mercado no varejo alimentar : uma análise usando os preços do estado de São Paulo. Rev. Econ. Sociol. Rural, v. 49, n. 4, p. 967–990, 2011.

BARRETT, C. B. Measuring integration and efficiency in international agricultural markets. Review of Agricultural Economics, v. 23, n. 1, p. 19–32, 2001.

BARRO, R. J.; SALA-I-MARTIN, X. Convergence across states and regions. Brookings Papers on Economic Activity, v. 22, n. 1, p. 107–182, 1991.

BARRO, R. J.; SALA-I-MARTIN, X. Convergence. Journal of Political Economy, v. 100, n. 2, p. 223, 1992.

BARRO, R. J. AND SALA-I-MARTIN, X. Economic Growth, McGraw-Hill, New York, 1995.

BUKENYA, J. O.; LABYS, W. C. Price Convergence on world commodity markets: fact or fiction? International Regional Science Review, v. 28, n. July, p. 302–329, 2005.

CIOFFI, A.; GAETANO, F.; DAMIANO, C. The price stabilization effects of the EU entry price scheme for fruit and vegetables. Agricultural Economics, v. 42, p. 405–418, 2011.

DOBADO, R.; MARRERO, G. A. Corn market integration in Porfirian Mexico. Cambridge University Press Economic History Association, v. 65, n. 1, p. 103–128, 2005.

DREGER, C. et al. Price convergence in the enlarged internal market. Berlim: CASE Network Reports, 2007. 

EGGER, P.; PFAFFERMAYR, M. On testing conditional sigma-convergence. Oxford Bulletin of Economics and Statistics, v. 71, n. 4, p. 453–473, 2009.

ENKE, S. Equilibrium among spatially separated markets: solution by electric analogue. Econometrica, v. 19, n. 1, p. 40, jan. 1951.

FIGUEIREDO, A. M.; SOUZA-FILHO, H. M. de; GUANZIROLI, C. E. VALENTE-JUNIOR, A. S. Análise da transmissão de preços no mercado brasileiro de castanha de caju. Revista Econômica do Nordeste, v. 41, n. 4, p. 716-730, 2010.

FIGUEIREDO, A. M.; SOUZA-FILHO, H. M.; PAULLILO, L. F. O. Análise das margens e transmissão de preços no sistema agroindustrial do suco de laranja no Brasil. Rev. Econ. Sociol. Rural, v. 51, n. 2, p. 331–350, 2013.

FRIEDMAN, M. Do old fallacies ever die?. American Economic Association, v. 30, n. 4, p. 2129–2132, 1992.

GARCÍA-HIERNAUX, A.; GUERRERO, D. E.; MCALEER, M. Market integration dynamics and asymptotic price convergence in distribution. Economic Modelling, v. 52, p. 913–925, jan. 2016.

IM, S. K.; PESARAN, M. H.; SHIN, Y. Testing for unit roots in heterogeneous panels. Journal of Econometrics, v. 115, p. 53–74, 2003.

ISLAM, N. What have we learnt from the convergence debate ? Journal of Economic Surveys, v. 17, n. 3, p. 309–362, 2003.

KIM, H.; RYU, D. Measuring the speed of convergence of stock prices: a nonparametric and nonlinear approach. Economic Modelling, v. 51, p. 227–241, 2015.

KULIKOV, D. Law of One Price in the euro area: an empirical investigation using Nielsen disaggregated price data. Working Paper Series, 2014.

LEVIN, A.; LIN, C. F.; CHU, C. S. J. Unit root tests in panel data: asymptotic and finite-sample properties. Journal of Econometrics, v. 108, n. 1, p. 1–24, 2002.

LINDENBLATT, A.; FEUERSTEIN, S. Price convergence after the Eastern enlargement of the EU: evidence from retail food prices. European Review of Agricultural Economics, v. 42, n. 5, p. 829–849, 2015.

MADDALA, G. S.; WU, S. A comparative study of unit root tests with panel data and a new simple test. Oxford Bulletin of Economics and Statistics, v. Special, p. 631–652, 1999.

MATTOS, L. B. et al. Modelos de cointegração com um ou dois limiares: Uma aplicação para o preço do frango inteiro resfriado em mercados atacadistas no Brasil. Revista de Economia e Sociologia Rural, v. 48, n. 4, p. 597–617, 2010.

MATTOS, L. B.; LIMA, J. E.; LÍRIO, V. S. Integração espacial de mercados na presença de custos de transação: um estudo para o mercado de boi gordo em Minas Gerais e São Paulo. Revista de Economia e Sociologia Rural, v. 47, n. 1, p. 249–274, 2009.

MAYORGA, R. D. O. et al. Análise de transmissão de preços do mercado atacadista de melão do Brasil. Revista de Economia e Sociologia Rural, v. 45, n. 03, p. 675–704, 2007.

MAYORGA, R. D. O. et al. Relacionamento de preços no mercado nordestino de tomate. Revista de Economia e Agronegócio, v. 7, n. 1, p. 77–102, 2009.

PENNA, C.; LINHARES, F. Uma nota sobre “ teste da convergência do PIB per capita da agropecuária no Brasil ”. Revista de Economia e Sociologia Rural, v. 51, n. 1, p. 091–104, 2013a.

PENNA, C.; LINHARES, F. Há Controvérsia entre análises de beta e sigma-Convergência no Brasil ? Revista Barsileira de Economia, v. 67, n. 1, p. 121–145, 2013b.

PFAFFERMAYR, M. Regional science and urban economics conditional β - and σ -convergence in space : a maximum likelihood approach. Regional Science and Urban Economics, v. 39, n. 1, p. 63–78, 2009.

QUAH, D. Exploiting Cross section variation for unit root inference in dynamic data. Economics Letters, v. 44, n. 1-2, p. 9–19, 1994.

SAMUELSON, P. A. American economic association. American Economic Association, v. 42, n. 3, p. 283–303, 1952.

SILVA, R. J.; MARGARIDO, M. A. Análise da transmissão espacial de preços no mercado de mandioca. Revista de Economia e Administração, v. 8, n. 4, p. 464–484, 2009.

SOARES, N. S.; SOUSA, E. P. DE; SILVA, M. L. DA. Análise de previsões de preços da castanha de caju no Ceará. Revista Economica do Nordeste, v. 43, n. 3, p. 448–500, 2012.

SOUSA, E. P. DE; CAMPOS, A. C. Efeitos e acordos sobre a integração de preços do algodão nos mercados interno e externo. Revista de Economia e Agronegócio, v. 7, n. 2, p. 173–196, 2009.

SPOHR, G.; FREITAS, C. A. de. Teste da convergência do PIB per capita da agropecuária no Brasil entre 1980 e 2004. Rev. Econ. Sociol. Rural, v. 49, n. 2, p. 341-368, 2011.

TABOSA, F. J. S.; IRFFI, G. D.; PENNA, C. M. Análise de clube de convergência para o mercado brasileiro do milho. Revista de Economia e Agronegócio, v. 11, n. 1, p. 235–254, 2014.

TABOSA, F. J. S.; FERREIRA, R. T.; CASTELAR, L. I. Convergência de mercados intrarregionais : o caso do mercado atacadista brasileiro do tomate. Revista de Economia e Sociologia Rural, v. 52, n. 1, p. 061–080, 2014.

WOLSZCZAK-DERLACZ, J. Price convergence in the EU - an aggregate and disaggregate approach. International Economics and Economic Policy, v. 5, n. 1, p. 25–47, 19 jul. 2008.

Anexo

Tabela 1A. Estatística Descritiva dos Preços dos Produtos, por Regiões.

Fonte: Elaboração dos autores. Obs.: Valores em negrito mostram a região que tem preço inferior naqueles produtos
em relação às outras regiões.  Nesta, foram excluídas da amostra dois centros: Campo Grande, região Centro-Oeste e
Belém, região Norte em virtude da falta de dados dos outros centros dessas regiões.

Tabela 2A. Testes de Estacionariedade, Levin-Lin-Chu, Im-Pesaram-Shin e Fisher-
Type para as séries de preços logaritmizadas, com tendência, de janeiro de 2007 a julho de 2015.

Fonte: Elaboração dos autores. * Significantes ao nível de 1%. ** Significantes ao nível de 5%.

1. Economista. Aluno do Mestrado de Economia Rural – UFC. E-mail: gerriosantos@gmail.com
2. Doutor em Economia, Professor do Curso de Mestrado em Economia Rural/MAER da Universidade Federal do Ceará (UFC). E-mail: franze@caen.ufc.br
3. Doutor em Economia, Professor do Curso de Mestrado em Economia Rural/MAER da Universidade Federal do Ceará (UFC). E-mail: jaraujoce@gmail.com