HOME | ÍNDICE POR TÍTULO | NORMAS PUBLICACIÓN

Espacios. Vol. 37 (Nº 27) Año 2016. Pág. 5

A Utilização dos Gráficos de Controle para Acompanhamento de Processos de Vigilância

Use of Control Processes for Monitoring Graphics in Surveillance

Roselaine Ruviaro ZANINI 1; Adriano Mendonça SOUZA 2; Luciane Flores JACOBI 3; Angélica PERIPOLLI 4; Sttefani Nikoli DAPPER 5; Ana Carolina Josende da SILVA 6

Recibido: 06/05/16 • Aprobado: 30/05/2016

Conteúdo

1. Introdução

2. Gráficos estatísticos de controle

3. Metodologia

4. Resultados

5. Conclusão

Referências

1. Introdução

Os métodos estatísticos são importantes recursos para detectar mudanças em vários tipos de processos. Dentre eles, destacam-se os gráficos de controle, desenvolvidos por Walter Shewhart (1924), usados em processos químicos e industriais, os quais usam procedimentos estatísticos para descrever a variabilidade e monitorar melhorias num processo (Benneyan, 1998). Entretanto, ao longo dos anos, esses gráficos têm sido teoricamente aprimorados e aplicados em muitas situações.

A aplicação dos métodos padrões de controle estatístico de processos de vigilância, no controle de infecções, na epidemiologia hospitalar, no tempo de espera para atendimento, na satisfação de pacientes e profissionais, entre outros, tem sido muito discutida na literatura (Sellick, 1993; Rossi, 1999; Benneyan, 1998; Sanches, 2000; Benneyan, 2001; Arantes, 2003, Morton, 2005; Burns, 2005).

Assim, existem muitas similaridades entre os objetivos e os métodos de controle da qualidade total (TQC) e os da Epidemiologia. Se o objetivo primário do TQC é melhorar os cuidados em saúde pela redução da variabilidade nos processos, o comportamento e a variabilidade do sistema devem ser explorados, com o uso das ferramentas do controle estatístico do processo (Benneyan, 1998).

Diante da analogia e da simplicidade de alguns métodos estatísticos de controle de qualidade, tem havido uma maior divulgação e incentivo para a aplicação dos mesmos na análise de dados na área da saúde, apesar de uma subutilização, na opinião de Reinke (1991).

Assim, este estudo tem por objetivo descrever e exemplificar alguns dos principais tipos de gráficos estatísticos de controle de qualidade utilizados na área industrial direcionados à área da saúde.

2.  Gráficos estatísticos de controle

Um método eficiente para monitorar e tentar reduzir a variabilidade de um processo consiste em construir gráficos estatísticos de controle, usados como uma ferramenta do Controle Estatístico de Processos (CEP) e como parte integrante das técnicas que buscam a qualidade de produtos ou serviços.

Os gráficos de controle revelam quando determinado processo sofre modificações e necessita de alguma intervenção. Foram desenvolvidos, inicialmente, pelo Dr. Walter Shewhart, com o objetivo de fazer distinção entre variabilidade controlável e não-controlável, devido a causas que afetam o desempenho do processo - causas comuns e especiais.

Segundo Siqueira (1997), as causas comuns referem-se às muitas fontes de variação atuantes no processo sob controle estatístico. Correspondem à soma dos efeitos de pequenas causas inevitáveis inerentes, ou seja, estarão presentes mesmo que procedimentos adequados sejam implementados. Por outro lado, as causas especiais referem-se a fontes que causam variabilidade nas medidas e que não podem ser adequadamente explicadas por qualquer distribuição, como seria se o processo estivesse sob controle, sendo consideradas não usuais e podem ser eliminadas. Assim, quando o processo estiver controlado é possível concluir e prever, significativamente, em relação ao desempenho do mesmo.

2.1 Elementos de um gráfico de controle

Um gráfico de controle é representado, basicamente, por três linhas paralelas e horizontais, dispostas num eixo cartesiano. A linha central (LC) representa o valor médio da característica sob investigação e as outras duas linhas, representadas, simetricamente em relação à linha central e a uma distância de três desvios-padrões (), são os limites inferior (LIC) e superior (LSC) de controle. Os pontos incluídos no gráfico representam as médias ou as medidas de cada subamostra.

Para que os resultados dos gráficos sejam válidos, as observações devem ser independentes e identicamente distribuídas, seguindo uma distribuição de probabilidade específica. Essas suposições embasam o cálculo dos limites de controle e as regras para identificação de padrões não aleatórios.

Nas situações em que não ocorra a independência entre as observações, ou seja, na presença de autocorrelação, Montgomery (1997) sugere outros procedimentos, como, por exemplo, ajustar um modelo de séries temporais do tipo ARIMA (Autorregressivo Integrado de Média Móvel) e, posteriormente, aplicar os gráficos de controle aos resíduos do modelo.

2.2 Funções dos gráficos de controle

Segundo Montgomery (1997), as principais funções são: (i) emitir sinal sobre a presença de causas especiais de variação, de tal forma que ações corretivas possam ser tomadas para trazer o processo para o estado de controle estatístico; (ii) fazer com que o processo obtenha alta qualidade e capacidade, com baixo custo unitário; (iii) controlar o processo ao longo do tempo; (iv) fornecer indicação se os problemas que afetam o processo são devido a falhas locais (forma que o processo está sendo operado) ou falhas de sistema (projeto, construção e manutenção); (v) auxiliar ao operador na decisão de intervir ou não no processo e (vi) fornecer evidência se o processo está operando num regime de controle estatístico, de tal forma que se possa fazer o cálculo da capacidade do processo de atender às especificações.

As principais indicações da presença de causas especiais ou assinaláveis são: (i) pontos fora dos limites de controle indicam a presença de uma causa especial e, sempre que possível, o motivo e a ação corretiva deveria ser indicada; (ii) um deslocamento, ou seja, uma mudança de nível indica que o processo se deslocou em relação àquela característica avaliada; (iii) uma tendência, ou seja, um aumento ou queda gradual no nível dos pontos no gráfico, indicam que o processo está se alterando e (iv) os ciclos, que são padrões consistentes de pontos de altos e baixos que se repetem periodicamente.

2.3 Análise de padrões em gráficos de controle

Nos gráficos de controle, quando um ponto aparece fora dos limites estabelecidos, diz-se que o processo é instável, indicando a presença de uma causa especial ou que o ponto fora dos limites pertence a uma população diferente daquela para o qual os limites de controle foram estabelecidos. Porém, um processo pode ser considerado fora de controle, mesmo que todos os pontos caiam dentro dos limites. Isto ocorre quando um padrão de variação anormal está presente no processo.

Sintetizando, pode-se dizer que um padrão normal pode ser identificado se: (i) a maioria dos pontos estão próximos da linha central; (ii) poucos pontos se espalham e se aproximam dos limites de controle e (iii) nenhum dos pontos excede os limites.

A análise de padrões é importante para a determinação do grau de instabilidade de uma característica no processo ou das possíveis dificuldades amostrais. A violação de alguma dessas regras serve de alerta no sentido de investigar, descobrir e remover as causas especiais devido a esses pontos.

2.4 Gráficos de controle de Shewhart para a média e amplitude ( e R)

Os gráficos de controle ( e R) são usados para monitorar um processo cuja característica de qualidade de interesse é expressa em uma escala contínua de medida. O gráfico  representa o valor médio de um subgrupo e é utilizado com o objetivo de controlar a média do processo, enquanto o gráfico R controla a variação do mesmo. Estes gráficos devem ser empregados simultaneamente. A desvantagem desses gráficos é que eles requerem amostras pequenas e de mesmo tamanho.

A grande simplicidade do modelo clássico de Shewhart permitiu sua rápida difusão no sistema produtivo americano e, em seguida, de todo o mundo industrializado. Sua operacionalização, bastante simples e pressupõe poucos conhecimentos estatísticos.

Pontos fora dos limites de controle, no gráfico da média, evidenciam uma mudança geral, afetando todos os itens produzidos depois do primeiro subgrupo fora dos limites. Nesse caso, é necessário avaliar os registros mantidos durante a coleta, a operação do processo e a experiência do operário, tentando descobrir uma variável que poderia ter feito com que os subgrupos saíssem de controle. Algumas causas típicas são: mudanças na matéria-prima, no pessoal, ajuste de máquinas, desgaste de ferramentas, temperatura ou vibrações ocorridas no processo, segundo Juran (1962).

Segundo Montgomery (2000), a principal desvantagem dos gráficos de Shewhart é usar a última informação e ignorar qualquer informação dada pela seqüência completa dos pontos, fazendo com que sejam insensíveis a pequenos e contínuos desvios, da ordem de até 1,5 desvios-padrões.

2.5  Gráficos de controle de somas cumulativas (CUSUM)

Duas alternativas efetivas para o gráfico de controle de Shewhart podem ser usadas quando ocorrem pequenos desvios do valor nominal, como os gráficos de controle de somas cumulativas (CUSUM) e os gráficos de controle de médias móveis exponencialmente ponderadas (EWMA).

Estes gráficos acumulam a informação mais recente com as anteriores, e com isso, detectam desvios moderados no valor nominal utilizando um número médio de amostras menor do que se fossem utilizados os de Shewhart. São mais eficientes também quando n=1 (Montgomery, 1997).

Algumas aplicações de somas acumuladas são: (i) detectar mudanças na média de um processo contínuo, verificando o ponto de ocorrência e estimar a quantia de tais mudanças; (ii) classificar produções contínuas em categorias como defeituosa e não-defeituosa; (iii) pesquisar um conjunto de dados passados para ver quando ocorreram as mudanças na média; (iv) indicar mudanças e tendências e formar um sistema de previsão a curto prazo e (v) detectar mudanças na variabilidade.

Os gráficos CUSUM foram propostos por Page (1954), sendo uma ferramenta que acumula informações das amostras de um processo ponderando-as igualmente, podendo tanto ser usadas  para observações individuais quanto para observações amostrais das médias de subgrupos racionais.

No caso de observações individuais (n = 1), utiliza-se a soma cumulativa dos desvios de cada valor individual com relação à medida dada pela hipótese que está sendo testada. No caso de n>1, esta estatística é a soma cumulativa dos desvios da média amostral com relação ao valor nominal.

Além disso, muitas vezes é mais fácil de detectar o ponto no qual a mudança ocorre simplesmente pelo exame visual dos dados plotados, notando onde a mudança na inclinação ocorreu. Algumas desvantagens são: (i) o gráfico de somas cumulativas pode ser muito lento para detectar grandes mudanças em processos e (ii) não é um procedimento muito eficiente para analisar dados históricos, com o objetivo de detectar descontrole num processo ou para trazer o mesmo até o controle.

26 Gráficos de controle de médias móveis exponencialmente ponderadas (EWMA)

Substituindo-se, recursivamente, para Zi-j, com j = 2,3, ..., t, obtém-se:

2.7 Gráficos de controle para observações correlacionadas

2.8 Modelagem de Box e Jenkins para séries temporais

2.9 Aplicações dos gráficos de controle como ferramenta de gestão na saúde

Segundo Benneyan (1998) existem similaridades entre os objetivos gerais e métodos da engenharia de qualidade industrial e os da área da saúde, principalmente na Epidemiologia. Além disso, Benneyan (1995) discute similaridades e diferenças entre epidemiologia e métodos de controle de qualidade, além de possíveis dificuldades na aplicação desses de gráficos no controle de infecção.

McGuckin e Abrutyn (1979) descrevem um método de vigilância muito similar aos gráficos de controle, os quais foram usados para detectar epidemias e desencadear ações investigativas. Cullen et al. (1984) usaram gráficos de controle para detecção precoce de epidemia de malária no Tailândia.

Martone et al. (1991) fizeram distinções importantes em taxas de infecções para as diferentes clínicas (UTI adulto e infantil, pacientes cirúrgicos e pacientes de alto risco). Eles recomendaram que taxas de infecções fossem baseadas no número ou na duração sob risco (tal como o número de pacientes diários e cirurgias). Esse método se mostrou melhor do que usar  as admissões ou altas. Posteriormente, discutiram aproximações para aplicar a qualquer categoria de pacientes homogêneos. Reinke (1991) e Sellick (1993) também propuseram monitorar taxas de infecção sobre o tempo.

Costa (1995) realizou uma revisão de literatura e constatou o uso dos gráficos de Shewhart no estudo da epidemia de poliomielite no estado da Califórnia, na epidemia de doença meningocócica ocorrida em São Paulo, na caracterização de epidemias de influenza na Tailândia, na mortalidade por doença meningocócica em Londrina, no monitoramento da incidência da raiva no Paraná e de doenças como: coqueluche, tétano, sarampo e difteria na Secretaria de Saúde do Estado do Rio de Janeiro.

As técnicas das somas cumulativas são sensíveis a pequenas mudanças, tornando-se satisfatórias na detecção do tempo de início das epidemias ou na monitoração de séries de infecções incomuns. Assim elas são robustas quando são usadas nos dados da vigilância, podendo apresentar uma boa performance se o número de casos estiver aumentando rapidamente acima do usual.

Santos (1997) realizou estudo comparativo simulado, entre a carta de Shewhart e o procedimento de CUSUM, detectando boa sensibilidade e precocidade nos dois métodos. Uma revisão realizada por Sanches (2000) mostrou que o CUSUM foi aplicado na vigilância de má-formação congênita e de estudos em unidades de saúde; no controle da qualidade em radioimunoensaio e em química clínica; no monitoramento da temperatura corporal basal em mulheres em idade de procriar, de doenças isquêmicas do coração e de abortos espontâneos.

Brookmeyer e Stroup (2004) coordenaram ampla discussão sobre o monitoramento de saúde das populações, os princípios estatísticos e métodos para vigilância em saúde pública. Desse trabalho, pode-se destacar as técnicas para detecção de surtos, voltadas para aplicação na vigilância de doenças infecciosas, as quais são classificadas por Farrington (2004) em três métodos estatísticos principais: regressão; séries temporaise controle estatístico do processo.

Farrington (2004) relata que a detecção prospectiva de surtos de doenças infecciosas é similar à detecção de incoerências no processo de produção industrial. Por exemplo, vários métodos usados na vigilância de infecção hospitalar são similares aos gráficos de controle introduzidos por Shewhart em 1931. Esses gráficos são usados para traçar características do processo de produção em determinado tempo, como índice de qualidade e proporção de itens defeituosos. Na detecção de surtos, o processo, o número de eventos no tempo, e os limites de predição fazem o papel dos limites de controle.

2.10 Indicadores hospitalares de qualidade e produtividade

A definição mais simples da qualidade talvez seja aquela inspirada pelo trabalho de W. Edwards Deming, um pioneiro do movimento de qualidade na indústria. Em seu aspecto mais básico, fornecer boa qualidade significa fazer o que é correto e da forma correta (Blumenfeld, 1993). Na área de atendimento de saúde e planejamento familiar, significa oferecer serviços que sejam seguros e eficazes e que satisfaçam às necessidades e desejos do cliente.

De uma perspectiva de saúde pública, a qualidade significa oferecer os maiores benefícios de saúde com o menor nível de risco ao maior número de pessoas, dados os recursos disponíveis (Huber, 1994). Para outros, a qualidade significa oferecer uma série adequada de serviços, por exemplo, integrando serviços que tratam de doenças sexualmente transmissíveis e serviços de saúde maternal e infantil aos serviços de planejamento familiar. E ainda existem outros que definem a qualidade basicamente como a capacidade de satisfazer aos desejos dos clientes.

A boa qualidade pode significar, também, cumprir as normas mínimas de atendimento adequado ou alcançar altos padrões de excelência. A qualidade pode se referir à qualidade técnica do atendimento, aos aspectos não técnicos da prestação do serviço - por exemplo, quanto tempo o cliente tem que esperar, ou como é tratado pelo pessoal de atendimento - ou, ainda, aos elementos programáticos, tais como políticas, infra-estrutura, acesso e administração (Bruce, 1990; Donabedian, 1980).

Historicamente, para os profissionais de saúde, a qualidade significa qualidade clínica do atendimento, ou seja, poder atender de forma competente, eficaz e segura, poder contribuir para o bem-estar de um indivíduo (Diprete et al., 1993). De sua parte, os gerentes de programas reconhecem que os serviços de apoio são também importantes para a qualidade da prestação dos serviços. Para os responsáveis pela elaboração de políticas e doadores, outros elementos importantes incluem o custo, a eficácia e os resultados obtidos para a população como um todo (Hull, 1996; Newbrander, 1997).

A definição de qualidade da Organização Mundial da Saúde (OMS) engloba as perspectivas de todos os grupos, e consiste em realizar intervenções de forma adequada, ou seja, que tenham sido confirmadas como seguras, pelas quais o público possa pagar e que possam ter impacto substancial sobre a taxa de mortalidade, morbidade, invalidez e desnutrição (Roemer, 1988).

O controle de qualidade garante que as atividades do programa ocorram conforme planejado. As atividades de controle da qualidade também poderão descobrir falhas no projeto e, assim, indicar mudanças que poderiam melhorar a qualidade (Buchanan, 1995; Kritchevsky, 1991). No campo da saúde, o objetivo principal é garantir que todo prestador de serviços ofereça sempre a mesma boa qualidade a todos os clientes (Kritchevsky, 1991, McGlynn, 1995).

O controle da qualidade inclui a supervisão e o monitoramento cotidianos, para confirmar que as atividades estejam sendo realizadas como planejado, e que o pessoal de atendimento esteja seguindo as diretrizes (Diprete et al., 1993). Os indicadores são instrumentos utilizados para avaliar o desempenho hospitalar, envolvendo organização, recursos e metodologia de trabalho. Os registros hospitalares transformam-se em instrumentos úteis para avaliação da assistência prestada, quantidade e tipo de recurso envolvido, controle dos custos gerados na produção dos serviços e grau de resolução dos mesmos (APM e CRM/SP, 1992).

Considerando que indicadores são reflexos de uma situação real e, portanto, medidas indiretas e parciais de uma situação complexa, quando calculados seqüencialmente, no tempo, podem indicar a direção e a velocidade das mudanças e servem para comparar diferentes áreas ou grupo de pessoas em um mesmo momento (Mello Jorge et al., 1992).

Uma ressalva a ser considerada é a grande dificuldade em definir e interpretar gold standards para a performance de hospitais. A alternativa é acompanhar indiretamente, com indicadores, o desempenho ao longo do tempo, na própria instituição e com outros hospitais. Para facilitar as comparações de dados e informações dentro e entre hospitais, a terminologia, as definições, o vocabulário e a nomenclatura utilizada devem estar acordados e padronizados, de maneira uniforme.

3. Metodologia

As variáveis utilizadas foram obtidas dos relatórios elaborados pelo setor de Estatística do Hospital Universitário de Santa Maria – HUSM,  no período de 2000 a 2005: taxa de ocupação do hospital geral (TOH), taxa de ocupação da unidade psiquiátrica (UP) e taxa de mortalidade institucional - diálise (TMI).

Após a coleta, a elaboração e a revisão do banco de dados foi realizada uma análise descritiva e testes de normalidade para as variáveis, usando o teste de Shapiro-Wilk. Para aquelas variáveis com presença de correlação serial foram ajustados modelos de séries temporais, usando a metodologia de Box e Jenkins, para posterior construção dos gráficos de controle nos resíduos das mesmas.

Para identificar o modelo adequado, inicialmente, apresentou-se o gráfico da série original, para verificar possível falta de estacionariedade. Em caso afirmativo, foi realizada uma diferenciação na mesma para estacionarizá-la, antes de prosseguir a modelagem.

Posteriormente foram construídos os gráficos de autocorrelação (ACF) e autocorrelação parcial (PACF) para identificar o tipo e o número de parâmetros, sendo que foram selecionados, entre os de ruído branco, aqueles que apresentaram os menores valores dos critérios de AIC e BIC.

Para as séries que seguiram a normalidade foram construídos gráficos de controle para medidas individuais. As análises estatísticas foram realizadas com o uso do software Statistica 9.1.

4.  Resultados

Procedeu-se inicialmente uma análise descritiva das variáveis, analisando-se os pressupostos e, os resultados, estão na Tabela 1.

Tabela 1 – Estatística descritiva das variáveis analisadas

Diante da presença de autocorrelação serial em TOH UP, não foi atendido o pressuposto de independência das observações, o que impossibilitou o uso dos gráficos de controle. Assim, foi ajustado um ARIMA para, posteriormente, aplicar os gráficos de controle nos resíduos dos modelos.

Para TMI aplicaram-se diretamente os gráficos de controle, devido à verificação de normalidade nos dados e ausência de autocorrelação serial.

4.1 Taxa de ocupação do hospital geral (TOH)

Na Figura 1 apresenta-se a taxa de ocupação do hospital geral, não estacionária em seu nível, corroborado pela funções de autocorrelações e autocorrelações parciais.  Neste caso, a série foi diferenciada para adequada utilização da metodologia de Box e Jenkins.

A partir da série com uma diferença, pode-se observar uma oscilação em torno de uma média constante, possibilitando o ajuste de um modelo ARIMA.

Figura 1 – Taxa de ocupação do hospital geral, de 2000 a 2005 no HUSM

Figura 2 – Gráfico de controle da taxa de ocupação do hospital geral

A análise da Figura 2 revela que ocorreram causas especiais de variação em muitos pontos. Após a eliminação desses pontos, alguns deles ainda permaneceram fora dos limites. Uma análise inicial levaria à tomada de decisões que poderiam não ser adequadas ao processo, como o aumento de custos ou mudanças de pessoal, isto porque não está sendo considerada a autocorrelação serial.

Assim, uma alternativa é construir os gráficos para os resíduos do modelo. Considerando-se o gráfico X e R, verificou-se apenas um ponto indicando causa especial de variação, conforme a Figura 3, demonstrando que o processo não está tão instável quanto parece ao se observar a Figura 2.

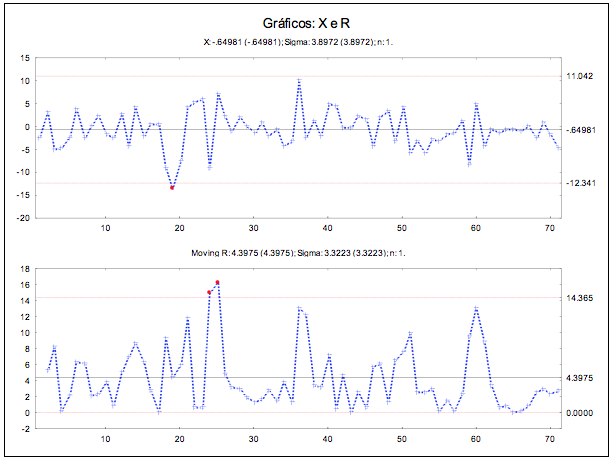
Figura 3 – Gráfico de controle dos resíduos da taxa de ocupação do hospital geral

Retirando esse ponto, não se observou nenhuma causa especial de variação para medidas individuais e dois pontos para o gráfico de amplitude móvel, conforme Figura 4.

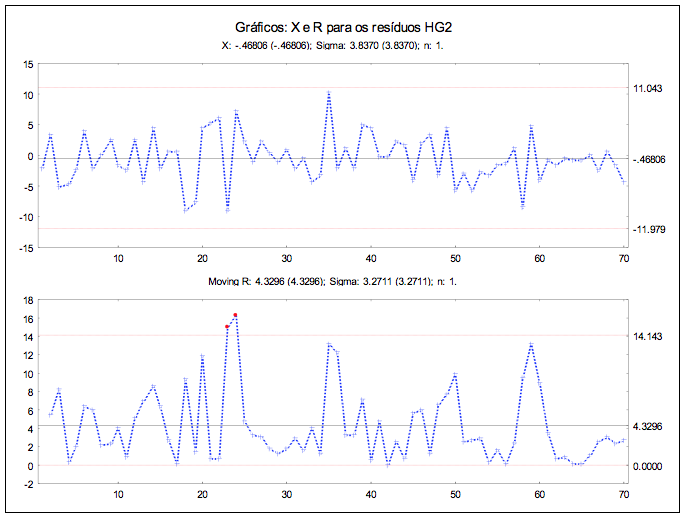
Figura 4 – Gráfico 2 de controle dos resíduos da taxa de ocupação do hospital geral

Na análise de padrões, apesar de não se observar nenhum ponto fora dos limites, identificou-se 5 pontos consecutivos (20 a 24) na faixa B, quando o processo se manteve fora de controle.

4.2 Taxa de ocupação da unidade psiquiátrica (UP)

Na Figura 5 apresenta-se a série da taxa de ocupação unidade psiquiátrica, na qual se observa que a ela não é estacionária em seu nível. Nesse caso, a série foi diferenciada para obtenção da estacionariedade pressuposta na metodologia de Box e Jenkins.

Figura 5 – Taxa de ocupação da unidade psiquiátrica, de 2000 a 2005 no HUSM

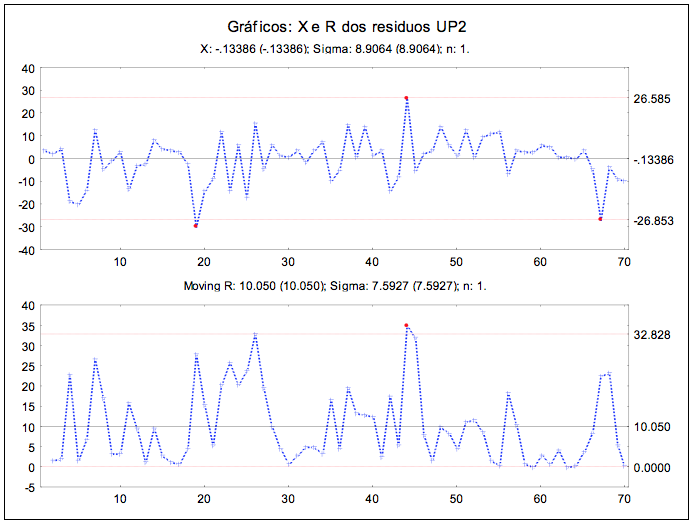
Figura 6 – Gráfico de controle dos resíduos da taxa de ocupação da UP

4.3 Taxa de mortalidade institucional – diálise (TMI)

Inicialmente foram construídos os gráficos X e R, para medidas individuais ( Figura 7), identificando-se duas observações fora dos limites, seguido do CUSUM e EWMA.

Figura 7 – Gráfico de medidas individuais da taxa de mortalidade institucional - diálise

Retirando essas observações, ainda assim, o processo não permaneceu estável. Considerando-se padrões especiais, encontrou-se 9 pontos consecutivos na faixa C (32 a 40 e 56 a 67); 3 pontos consecutivos na A (23 a 25 e 26 a 28) e 5 pontos consecutivos na B (19 a 23 e 24 a 28). Verificaram-se muitos pontos fora dos limites no gráfico CUSUM (Figura 8). O processo se manteve fora de controle praticamente durante todo o período, estabilizando apenas no último ano.

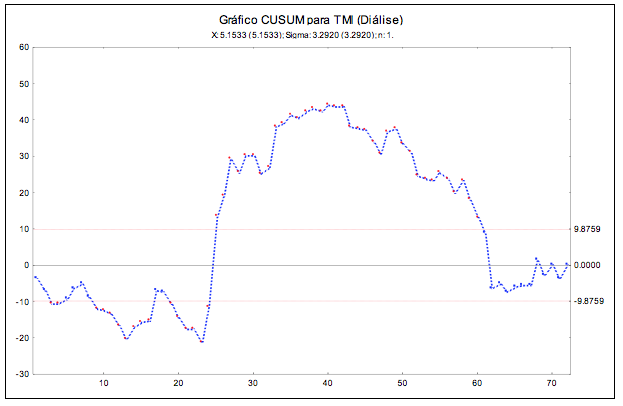
Figura 8 – Gráfico CUSUM da taxa de mortalidade institucional-diálise

No gráfico EWMA (Figura 9), pode-se observar que apenas alguns pontos no início do período analisado excederam os limites de controle, quando a constante de ponderação foi 0,05.

Figura 9 – Gráfico EWMA da taxa de mortalidade institucional-diálise (L=2,7, =0,05)

Quando se considerou l=0,10, identificou-se mais alguns pontos fora dos limites (Figura 10).

O gráfico CUSUM também foi mais eficiente na detecção precoce de pontos fora dos limites.

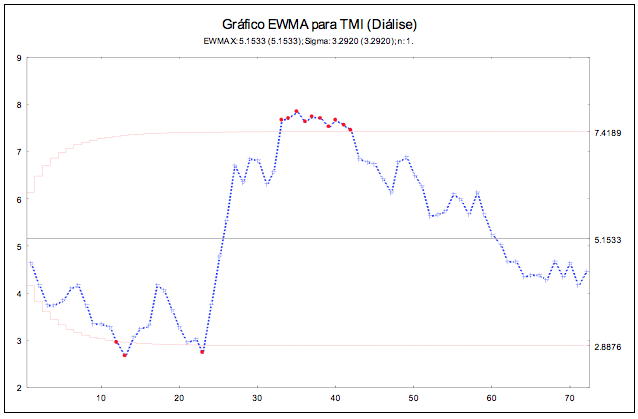
Figura 10 – Gráfico EWMA da taxa de mortalidade institucional-diálise (L = 2,7, l = 0,10)

5. Conclusão

A elaboração desse trabalho desenvolve-se em várias etapas: a apresentação da metodologia específica de diversos tipos de gráficos de controle, o estabelecimento das semelhanças entre os conceitos da área da saúde com os do CEP, a modelagem de algumas séries obtidas junto ao Hospital Universitário de Santa Maria e a aplicação de alguns dos gráficos de controle abordados.

Com a aplicação da metodologia de Box e Jenkins para séries temporais e a construção de gráficos de controle, verificou-se que os métodos apresentados constituem um importante suporte de orientação e apoio para os profissionais envolvidos no gerenciamento de processos na área da saúde.

Além disso, desconsiderar a autocorrelação, quando se utiliza a metodologia de gráficos de controle pode ter as seguintes conseqüências: (i) identificar causas especiais quando na realidade elas não existem e o processo se encontra sob controle; (ii) considerar o processo sob controle estatístico, quando existem causas especiais de variação presentes no processo; (iii) estimar incorretamente os parâmetros do processo; (iv) classificar incorretamente o processo em relação à capacidade do mesmo e (v) investigar as causas de problemas que não existem, levando ao desperdício de recursos e tempo.

Além disso, os gráficos X e R propiciam uma implementação mais simples, mas são ineficientes para detectar pequenos desvios e insensíveis para emitir sinal de alerta preventivo. Por outro lado os gráficos EWMA e, especialmente, os gráficos CUSUM são mais eficientes para detectar pequenos desvios e, em tempo real, emitem sinais de alerta precoces mais rapidamente que os demais.

Entretanto, superadas as dificuldades de treinamento dos profissionais e da implementação computacional, os benefícios seriam significativos, devido ao grande número de variáveis que poderiam ser controladas num ambiente hospitalar ou em qualquer outro setor de saúde.

Nessa pesquisa, observa-se que existe autocorrelação serial e grande variabilidade na maioria das séries estudadas, o que dificultaria a implementação de gráficos mais simples.

Foram identificados vários pontos fora dos limites de controle para a taxa de ocupação do hospital geral e para a mortalidade institucional por diálise. As taxas de ocupação da unidade psiquiátrica foram as que se mostraram mais estáveis.

Espera-se que esse trabalho possa colaborar  na melhoria dos processos que envolvem a área da saúde. Deve-se ressaltar que qualquer intervenção no sentido de melhorar a saúde das pessoas é de extrema importância, devido à repercussão que isso trará para os beneficiados em outros setores, como o pessoal, o familiar e no âmbito profissional.

Referências

Arantes, A.; Carvalho, E.S.; Medeiros, E.A.S.; Farhat, C.K.; Mantese, O.C. (2003). Uso de diagramas de controle na vigilância epidemiológica das infecções hospitalares. Revista de Saúde Pública, 37(6), 768-774.

APM/CRM-SP - Associação Paulista de Medicina & Conselho Regional de Medicina do Estado de São Paulo. (1992). Programa de Avaliação e Controle da Qualidade do Atendimento Médico-Hospitalar. I(3). São Paulo: Informativo CQH.

Benneyan, J.C. (1998). Statistical quality control methods in infection control and hospital epidemiology. In Part I: Introduction and basic theory. Infection Control and Hospital Epidemiology, 19(4), 194-214.

Benneyan, J.C. (1998). Statistical quality control methods in infection control and hospital epidemiology. In Part II: Chart use, statistics properties, and research issues. Infection Control and Hospital Epidemiology, 19(4), 265-283.

Berthouex, T.M.; Hunter, W.G.; Pallesen, L. (1978). Monitoring sewage treatment plants: some quality control aspects. Journal of Quality Technology, 10.

Blumenfeld, S.N. (1993). Quality assurance in transition. Papua New Guinea Medical Journal, 36(2), 81-89.

Box, G.E.P., Jenkins, G.M.( 1976). Time series analysis. San Francisco: Holden-Day.

Brookmeyer, R; Stroup, D.F. (2004). Monitoring the health of populations: statistical principles & methods for public health surveillance. New York: Oxford University press.

Bruce, J.( 1990). Fundamental elements of the quality of care: A simple framework. Studies in Family Planning, 21(2), 61-91.

Buchanan, F.D.; Batalden, P.E. (1995). Knowledge for improvement: Initiating continual improvement at the Hospital Corporation of America (pp.99-114). En Goldfield, N. and Nash, D.H., eds. Providing quality care: Future challenges.(2nd ed.), Michigan: Health Administration Press.

Burns, C.M.; Bennett, C.J.; Myers, C.T.; Ward, M. (2005). The use of CUSUM analysis in the early detection and management oh hospital bed occupancy crises. The Medical Journal of Australia, 183(6), 291-294.

Costa, A.J.L. (1995). Revisão das Técnicas Estatísticas propostas na Literatura para Detecção de Epidemias de Doenças Infecciosas. (Dissertação de Mestrado em Saúde Coletiva). Universidade do Estado do Rio de Janeiro. Rio de Janeiro.

Crowder, S.V. (1987). Average runs lenghts of exponentially weighted moving average control charts. Journal of Quality Technology, 19, 161-164.

Cullen, J.R.; Chitprarop, U.; Doberstyn, E.B.; Somebatwattanangkul, K. (1984). An epidemiological early warning system for malaria control in northern Thailand. Bulletin of the World Health Organization, 62(1), 107-114.

Diprete, B.L.; Franco, L.M.; Rafeh, N.; Hatzell, T. (1993). Quality assurance of health care in developing countries. Bethesda, Maryland: Quality Assurance Project, Center for Human Services.

Donabedian, A. (1980).  The definition of quality: A conceptual exploration. En  Explorations in quality assessment and monitoring: The definition of quality and approaches to its assessment (vols.1, pp.3-28). Ann Arbor, Michigan: Health Administration Press.

Farrington, P.A.N. (2004). Outbreak detections: application to infectious disease surveillance. En Brookmeyer, R; Stroup, D.F. Monitoring the health of populations: statistical principles & methods for public health surveillance (pp.203-230). New York: Oxford University press.

Huber, D. (1994). Proposed approach for medical quality of care in family planning/reproducte health services supported. Pathfinder International.

Hull, V.J. (1996). Improving quality of care in family planning: How far have we come? Jakarta, Indonesia, Population Council (n. 5). South and East Asia Regional Working Papers.

Hunter, J.S. (1986). The exponentially weighted moving average. Journal of Quality Technology, 18, 203-210.

Juran, J.M. (1962). Quality control handbook. New York: Mc Graw-Hill.

Kritchevsky, S.B.; Simmons, B.P. (1991). Continuous quality improvement: Concepts and applications for physician care. Journal of the American Medical Association, 255(13), 1817-1823.

Liao, W.S.; Wu, S.M.; Ermer, D.S. (1982). A time series approach to quality assurance. Inspection and Quality Control in Manufacturing Systems, vols.5, ASME.

Lucas, M.J.; Saccucci, M.S.(1990).  Exponentially weighted moving average control schemes: properties and enhancements. Technometrics, 32(1), 1-12.

Martone, W.J.; Gaynes, R.P.; Horan, T.C.; Emori, T.G.; Jarvis, W.R.; Bennet, M.E. et al. (1991). Nosocomial infections rates for interhospital comparison: limitations and possible solutiosns. Infection Control Hospital and Epidemiology, 12, 609-621.

Mcguckin, M.B.; ABRUTYN, E. (1979). A surveillance method for early detection of nosocomial outbreaks. American Journal of Infectology Control, 7, 18-21.

Mello-Jorge, M.H.P.; Gotlieb, S.L.D.; Soboll, M.L.M.S.; Baldijão, M.F.A.; Latorre, M.R.D. (1992). O sistema de informação sobre nascidos vivos – SINASC (MS/USP/OPAS-OMS - Série Divulgação, nº 7). São Paulo: Centro da OMS para Classificação de Doenças em Português.

Mcglynn, E.A. (1995). Quality assessment of reproductive health services. Western Journal of Medicine, 163(3), 19-27.

Montgomery, D.C. (1997). Introduction to statistical quality control. (3rd ed.). New York: John Wiley & Sons Inc.

Montgomery, D.C.( 2000).  Introduction to statistical quality control. (4 ed.). New York: John Wiley & Sons Inc.

Morton, A. (15,out,2005). Methods for hospital epidemiology and healthcare quality improvement: control charts [Part 1]. Recuperado de http://www.eicat.com/CHAPTER4.PDF

Newbrander, W.; Rosenthal, G. (1997). Quality of care issues in health sector reform. En Private health sector growth in Asia: Issues and implications (pp.177-195). Chichester, England, John Wiley and Sons. 

Page, E.S. (1954). Continuous Inspection Schemes. Biometrika, 41, 100-115.

Reinke, W.A. (1991).  Applicability of industrial sampling techniques to epidemiologic investigations: examination of an underutilized resource. American Journal of Epidemiology, 134(10), 1222-1232.

Roberts, S.W. (1959). Control chart tests based on geometric moving averages. Technometrics, 1, 239-250.

Roemer, M.I.; Montoya-Aguilar, C. (1988). Quality assessment and assurance in primary health care. Geneva: World Health Organization (WHO Offset Publication n.105).

Sanches, O. (2000). Princípios básicos de procedimentos estatísticos aplicados na análise de dados de vigilância em saúde pública: uma revisão. Cadernos de Saúde Pública, 16(2), 317-333.

Santos, M.O. (1997). A Utilização da Técnica de Somas Cumulativas (CUSUM) na Análise de Dados de Vigilância em Saúde Pública. (Dissertação de Mestrado em Saúde Pública). Fundação Oswaldo Cruz - Escola Nacional de Saúde Pública. Rio de Janeiro.

Sellick, J.A. (1993). The use of statistical process control charts in hospital epidemiology. Infection Control and Hospital Epidemiology, 14(11), 649-656.

Shewhart, W.A. (1931). Economic control of quality of manufactured product. Princeton, NJ: D. Van-Nostrand Reinhold.

Siqueira, L.G. P. (1997). Controle estatístico do processo. Série: Qualidade Brasil, São Paulo: Pioneira.

1. Programa de Pós-Graduação em Engenharia de Produção (PPGEP), Universidade Federal de Santa Maria – UFSM, Brasil, rrzanini@smail.ufsm.br
2. Programa de Pós-Graduação em Engenharia de Produção (PPGEP), Universidade Federal de Santa Maria – UFSM, Brasil
3. Departamento de Estatística, Universidade Federal de Santa Maria – UFSM, Brasil

4. Programa de Pós-Graduação em Engenharia de Produção (PPGEP), Universidade Federal de Santa Maria – UFSM, Brasil

5. Programa de Pós-Graduação em Engenharia de Produção (PPGEP), Universidade Federal de Santa Maria – UFSM, Brasil

6. Programa de Pós-Graduação em Engenharia de Produção (PPGEP), Universidade Federal de Santa Maria – UFSM, Brasil