HOME | ÍNDICE POR TÍTULO | NORMAS PUBLICACIÓN

Espacios. Vol. 37 (Nº 27) Año 2016. Pág. 3

Índices de competição dependentes da distância do estrato arbóreo na Amazônia brasileira

Distance dependent indexes of the arboreal stratum in the Brazilian Amazon

Silvane VATRAZ 1; Denis ALDER 2; José Natalino Macedo SILVA 3

Recibido: 06/05/16 • Aprobado: 26/06/2016

Conteúdo

1. Introdução

2. Revisão de literatura

3. Material e métodos

4. Resultados e discussão

5. Conclusão

Referências

1. Introdução

A obtenção de informações mais precisas das estimativas de produção de uma floresta natural é uma tarefa árdua, pois muitos fatores estão envolvidos no processo de crescimento da mesma, como os fatores climáticos, edáficos, topográficos, as características genéticas das árvores e dos mecanismos de competição (Prodan et al., 1997). Estes mecanismos, bem como a complexidade dos ecossistemas, devem ser bem compreendidos para que se possa planejar a produção sustentável dos recursos florestais.

As árvores em uma floresta natural tropical estão em contínuo estado de competição, seja pelo espaço aéreo em busca da luz, ou no solo pela água, minerais e oxigênio. Sob estas condições e na medida em que crescem de tamanho, as árvores tendem a apresentar uma diminuição das taxas de crescimento.

Os estudos sobre o crescimento das árvores em florestas na Amazônia têm sido um dos principais esforços dos pesquisadores ao longo destas últimas décadas e avaliação da competição vem de encontro com esse esforço.  Os índices de competição objetivam expressar o efeito da competição no crescimento das árvores (Pedersen et al., 2013). Para que isso seja possível, a maioria dos índices se relaciona a quatro fatores principais: número de competidores; tamanho e distância das árvores vizinhas e a luminosidade (Vanclay, 1994).

Os índices de competição podem ser divididos em dois grandes grupos, os independentes da distância (IID) que não consideram o posicionamento das árvores dentro da parcela, e dependentes da distância (IDD), que consideram a posição relativa entre as árvores na parcela e o seu tamanho (Peng, 2000). Ambos os métodos têm sido aplicados em florestas mistas ou ricas em espécies, porém, a literatura não indica claramente que tipo de índice é mais eficaz (Weiskittel et al., 2011).

Muitas abordagens têm sido utilizadas para definir a área de competição dos índices dependentes da distância, como por exemplo, o método de raio fixo (Burkhart e Tomé, 2012). No entanto, segundo Chassot (2013) não existe uma definição do tamanho de raio a ser utilizado para a identificação das árvores competidoras.

Outro ponto a se considerar é que os índices dependentes da distância tornam-se cada vez mais incompletos e imprecisos, à medida que as árvores se aproximam da borda da parcela, devido ao desconhecimento das árvores competidoras que estão fora da parcela, por isso é recomendado que se utilize o método de deslocamento (Shifting) para a correção da bordadura (Alder, 1995; Pretzsch, 2009).

A avaliação da efetividade de um índice de competição é realizada por meio da correlação do índice calculado para cada árvore com variáveis da floresta, como o incremento em diâmetro, altura e outros (Martins et al., 2011; Castro et al., 2014).

Portanto, o objetivo deste trabalho é o de avaliar dois índices dependentes da distância em diferentes raios de competição e identificar aqueles que mais se correlacionam com o diâmetro a 1,30m do solo em centímetros (DAP) e o incremento em DAP em cm.ano-1 (∆DAP). Os melhores resultados deverão apontar o índice mais adequado para representar a competição entre as árvores do estrato arbóreo, fornecendo subsídios para a modelagem de florestas, auxiliando o manejo florestal sustentável na floresta amazônica.

2. Revisão de literatura

Competição

A competição é uma relação ecológica de interação entre dois indivíduos que disputam o mesmo recurso. Ocorre geralmente quando os recursos são limitados (Mcnaughton e Wolf, 1973), contribuindo para a diminuição global da taxa de crescimento, do metabolismo, da sobrevivência ou da adequação daquele organismo abaixo de sua condição ideal (Welden e Slauson, 1986).

Dizemos que a competição é intraespecífica quando estão envolvidos indivíduos da mesma espécie e que é interespecífica quando se trata de espécies diferentes (Begon, Harper e Townsend, 1996).

A interação interespecífica pode se utilizar de dois mecanismos biológicos diferentes. A primeira é a interação física direta, mais conhecida como competição por interferência. Ela ocorre quando um indivíduo impede de forma direta outros organismos de explorarem um recurso (Begon, Harper e Townsend, 1996). E a segunda, a competição por exploração, que ocorre quando uma espécie explora um recurso em comum à outra espécie, mas sem contato direto com aquela espécie. Essa exploração indireta de recursos pode determinar uma vantagem competitiva de uma espécie à outra (Odum e Barret, 2007). 

Os resultados da competição têm sido muito estudados como um dos mecanismos da seleção natural, pois, a competição interespecífica pode resultar em um ajuste do equilíbrio entre duas espécies ou, se severa, pode fazer com que a população de uma espécie substitua outra. A tendência de a competição produzir uma separação ecológica de espécies aparentadas ou semelhantes é conhecida como o princípio da exclusão competitiva. No entanto, simultaneamente, a competição aciona várias adaptações seletivas que aumentam a coexistência de uma diversidade de organismos em uma dada área (Odum e Barret, 2007). Para fazer valer a coexistência em sistemas naturais, não apenas as diferenças de disponibilidade de recursos nos nichos devem ser consideradas, mas também a forma como as espécies respondem a estas variações no ambiente. Os conflitos funcionais, por sua vez, são também de grande importância ao fazerem com que cada espécie se dê melhor em pelo menos alguma combinação de condições, evitando que o ambiente seja dominado por apenas uma única superior (Giacomini, 2007).

Portanto, a competição é um processo chave no estudo de populações e comunidades vegetais, pois quase todas as intervenções estão relacionadas com a manipulação desse fator ou de condições que o alteram (Schneider e Schneider, 2008).

Índices de competição

O efeito que a competição exerce sobre o crescimento das árvores pode ser expresso por meio de um índice, denominado índice de competição. Estes índices permitem quantificar o nível competitivo de uma árvore em relação às suas competidoras (Davis et al., 2005). Portanto, um índice de competição (IC) pode ser definido como sendo a tentativa de quantificar, em simples expressões, o efeito de plantas vizinhas sobre o crescimento de uma árvore individual (Vanclay, 2006).

Os índices dependentes da distância levam em consideração as coordenadas espaciais que são atribuídas para cada árvore, as quais permitem ponderar a competição entre cada árvore e as árvores vizinhas pela distância, sendo mais complexos e exigentes em termos de coleta de dados (Hynynen, 1995). A competição certamente é diferente entre duas árvores de grande porte e entre uma árvore de pequeno porte e uma de grande porte. Por isso o tamanho das árvores, a proximidade e a distribuição das árvores vizinhas devem ser conhecidos, para que o processo de competição seja melhor avaliado (Vanclay, 1994).

Para que se identifiquem as árvores competidoras, geralmente é atribuído ao redor da árvore em que se queira avaliar (árvore objetivo), um raio, que pode ser fixo ou variável. Nos modelos de IC de raio fixo, uma área circular é atribuída a cada planta e as árvores contidas nesse círculo são consideradas vizinhas. O raio é fixado de forma arbitrária, mas geralmente corresponde à área horizontal ocupada pelos indivíduos adultos (Roitman, 2011).

Por sua vez, estes raios podem ser classificados de duas maneiras: pelo espaço explícito e pelo implícito. Quando empregamos um espaço contínuo, ou seja, quando levamos em consideração a distância relativa entre as árvores, estamos tratando de uma medida explícita. Porém, quando não consideramos uma distância linear como padrão para determinar o raio de vizinhança, não se importando muito com a distribuição das árvores, mas sim com o número e tamanho de árvores ao redor da árvore objetivo, estamos tratando de uma medida implícita (Berger et al., 2008).

Os modelos explícitos atribuídos a árvores individuais são capazes captar as interações locais, a variabilidade individual, comportamento adaptativo, e distribuições heterogêneas de recursos e outros fatores ambientais (Deangelis e Gross, 1992; Grimm, 1999). Assim, eles têm sido empregados na ecologia florestal há mais de 30 anos; (Liu e Ashton, 1995), e várias novas abordagens têm sido propostas ao longo dos últimos 10 anos (Berger et al., 2008).

Muitas evidências empíricas suportam a premissa de que os índices de competição espacializados não são necessariamente melhores do que fórmulas independentes de distância (Lorimer, 1983; Busing e Mailly, 2004). Contudo, os autores argumentam que boa parte dessa evidência vem de florestas plantadas (Daniels, 1976; Martin e Ek, 1984) onde a distribuição espacial das árvores é regular e a competição por recursos é diminuída.  Porém, outros estudos mencionam que os resultados dos modelos espacializados são melhores, quando na projeção do crescimento das árvores (Pukkala, 1989). Desta forma, não existe um senso comum entre que tipo de índice apresenta o melhor desempenho. Talvez, os desempenhos possam variar devido às especificidades de cada floresta.

Uma recente classificação e avaliação dos índices dependentes da distância do tipo Hegyi são apresentados no trabalho de Weiskittel et al. (2011) e indicam vantagens quando se considera o tamanho relativo das potenciais árvores competidoras e a distância entre ela e as árvores objetivo.

Raios de competição e bordadura

Vários autores propuseram metodologias para quantificar a competição, as quais, em sua absoluta totalidade, levam em conta as árvores competidoras. No entanto, não existe uma definição clara de quais as árvores, suas características, a localização espacial e distância em relação à árvore de interesse, exercem efeito competitivo, ou seja, não há um tamanho de unidade amostral a ser utilizado para a identificação das árvores competidoras (Chassot, 2013).

Muitas abordagens têm sido utilizadas para definir esta área de competição. Alguns trabalhos relacionam a um raio de area fixo, como Hegyi (1974), que determinou o número de competidores utilizando um raio fixo de 3,05m a partir da árvore objetivo. Beland et al. (2003), empregou raios de 3 e de 6 metros, indicando maior correlação com o raio de 6 metros. Miina e Pukkala (2002), também trabalharam com um raio de 6 metros, Contreras, Affleck, Chung (2001), com um raio de 11 metros. Zhao et al. (2006), realizou alguns testes prévios em seu estudo e determinou que um raio de 25 metros seria o mais adequado para os seus estudos em área tropical.

Quando se utiliza de índices de competição baseados na distância, não se pode considerar que as árvores próximas ao limite das parcelas, não sofram interferência por outras árvores, pelo simples fato de estarem localizadas na bordadura do experimento. Por isso, Alder (1995) menciona que a bordadura é um problema inerente aos modelos dependentes da distância.

O método do Deslocamento (Shifting) para correção da bordadura (Pretzsch, 2009), produz uma cópia exata da parcela, que é deslocada para todos os lados e cantos da parcela, com o intuito de simular o efeito da competição das árvores que são desconhecidas e estão presentes fora da parcela (Pretzsch, 2009).

3. Material e métodos

A área de estudo está localizada na área florestal da empresa Jari Florestal S.A., pertencente ao Grupo Jari, na localidade Morro do Felipe, município de Vitória do Jari – AP (Figura 1). Segundo a classificação de Köppen (1948), o clima na região é do tipo Ami (Gomide, 1997). De acordo com Azevedo et al. (2012), a precipitação média anual é de 2.234 mm. A vegetação é do tipo Floresta Tropical de Terra Firme ou Floresta Ombrófila Densa (Veloso et al., 1991).

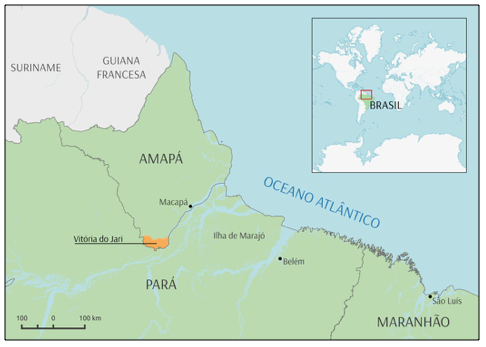
FIGURA 1 - Localização geográfica do município de Vitória do Jari- AP.
Fonte: Adaptado de IBGE, março de 2015.

Este estudo foi elaborado com dados do experimento originalmente denominado Projeto Bom Manejo (Embrapa/CIFOR/ITTO), desenvolvido pela Embrapa Amazônia Oriental. O experimento da Embrapa foi instalado em uma área de 500 ha, no ano de 1983. O mesmo monitorou a floresta entre os anos de 1984 a 2011 e as medições ocorreram em oito ocasiões, em 1984, 1986, 1988, 1990, 1994, 1996, 2004 e 2011. Por ocasião da colheita florestal em 1985, foram reduzidos cerca de 15% do volume comercial das árvores com DAP ≥ 60 cm, onde foram exploradas em média, cerca de três árvores por hectare. Em termos de volume, esta redução correspondeu a 26 m3ha-1.

Para estudar o desenvolvimento da floresta foram instaladas parcelas permanentes quadradas, medindo 100 m x 100 m (1,00 ha), onde foram medidos todos os indivíduos arbóreos com DAP ≥ 20,0 cm (Azevedo et al., 2012).

A metodologia empregada nas medições das parcelas permanentes seguem os padrões disponibilizados por Silva e Lopes (1984). As variáveis coletadas e empregadas neste estudo são: número da árvore, classe de identificação do fuste (CIF), medição do diâmetro a altura do peito (DAP), identificação botânica, situação silvicultural, iluminação de copas e as coordenadas cartesianas.

Índices de competição

Nos índices de competição descritos a seguir entende-se como “árvore objetivo” toda árvore que possui sua competição avaliada individualmente. Para o presente trabalho, todas as árvores existentes nas parcelas foram consideradas “árvores objetivo”. Foram avaliados e comparados os seguintes índices de competição (Tabela 1):

TABELA 1- Relação funcional dos Índices de competição dependentes da distância avaliados neste trabalho.

Em que: n = número de árvores com DAP maior que a árvore objetivo; di = DAP da árvore objetivo (cm);
dj= DAP da árvore competidora (cm); Lij= distância entre a árvore objetivo e a árvore competidora e nj= nº de árvores competidoras.

Distâncias entre árvores

A distância entre as árvores nos IDD foi calculada pela distância euclidiana a partir de suas coordenadas de posição (x e y). O cálculo dos índices foi operacionalizado por uma macro desenvolvida em ambiente Visual Basic for Applications (VBA) incorporada para uso no Microsoft Excel.

Raios de competição

Partindo da necessidade de se estabelecer um raio de competição em florestas naturais tropicais, entre a árvore objetivo e suas competidoras, foram testadas cinco distâncias de raios fixo, com: 3m, 5m, 10m, 15m e 20m. Estas distâncias foram definidas de forma arbitrária, no entanto, leva em consideração a dificuldade de se estabelecer raios de competição muito grandes, devido ao aumento do número de indivíduos vegetais não classificados no estrato arbóreo e, portanto não mensurados nos inventários florestais, o que poderiam de certa forma influenciar a estimativa da competição. Um esquema representando a área de competição pode ser visualizado na Figura 2.

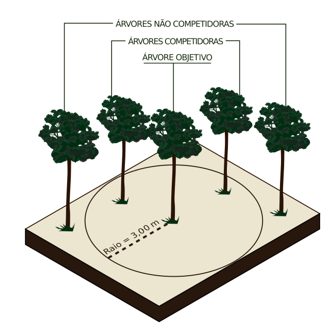
FIGURA 2- Representação do raio de competição dos índices dependentes da distância.

Bordadura

O efeito de bordadura nos IDD foi corrigido pelo método do deslocamento, conforme recomendado por Pretzsch (2009), representado na Figura 3. Este método consiste em emitir uma cópia exata da parcela, que é deslocada para todos os lados e cantos da mesma, com o objetivo de simular o efeito da competição das árvores que são desconhecidas e estão presentes fora da parcela.

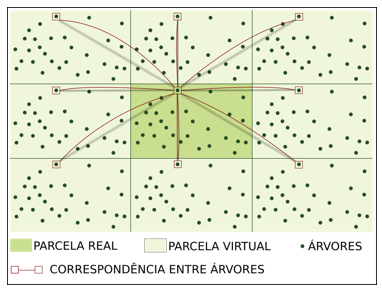
FIGURA 3- Esquema do método do deslocamento de parcelas (Shifting).
Fonte: própria

Cálculo do incremento diamétrico

 O incremento diamétrico foi obtido pela diferença entre as medidas de diâmetro das árvores com DAP > 20 cm, no período de 1984 e 2004, empregando a seguinte fórmula: (DAPfinal – DAPinicial) /T, em que T refere-se ao tempo entre as duas medições.

Avaliação dos índices de competição

A avaliação dos índices de competição se deu pela análise da correlação linear de Pearson (r), de forma a avaliar a correlação entre os índices calculados para cada árvore e as variáveis: o DAP e ∆DAP. A significância dos coeficientes foi baseada no valor de p, onde se o valor de p calculado for menor ou igual ao nível de significância (p <0,05) conclui-se que existe correlação linear e se for maior, não existe correlação (Triola, 2005; Devore, 2006). Os valores encontrados nas correlações foram avaliados pelo método de Dancey e Reidy (2006) que consideram resultados de r = 0,10 até 0,39, como uma correlação fraca; r = 0,40 até 0,69 uma correlação moderada e r = 0,70 até 1 uma correlação forte.

4. Resultados e discussão

Os índices de competição dependentes da distância testados neste trabalho indicaram de forma geral, uma tendência a apresentar valores maiores na medida em que são observados maiores valores de crescimento, no entanto, como são ponderados pela distância entre as árvores vizinhas e a árvore objetivo, o comportamento dos índices para os fustes de mesmo tamanho poder ser variado.

As correlações lineares dos índices dependentes da distância com as variáveis da floresta, testadas em cada raio podem ser visualizadas nas tabelas 2 e 3.

TABELA 2- Correlações lineares entre o índice de competição dependente da distância Hegyi e as variáveis diâmetro
a 1,30 m de altura (DAP) e incremento em diâmetro (∆DAP) em uma Floresta Ombrófila Densa, localizada em Vitória do Jari-AP.

HEG (3m)= Hegyi com raio de competição de 3m; HEG (5m)= Hegyi com raio de competição de 5m;
HEG (10m)= Hegyi com raio de competição de 10m; HEG (15m)= Hegyi com raio de competição de  15m e
HEG (20m)= Hegyi com raio de competição de 20m; p <0,05.

As maiores correlações com o índice de Hegyi ocorreram com um raio de 20 metros de distância. Onde foi detectada uma correlação moderada com a variável DAP (r= -0,618) e uma correlação fraca com a variável de incremento em DAP (r= -0,108). De forma geral, à medida que a distância do raio aumentava, as correlações ficavam mais altas.

TABELA 3- Correlações lineares entre o índice de competição dependente da distância Hegyi_modificado e as variáveis diâmetro
a 1,30 m de altura (DAP) e incremento em diâmetro (∆DAP) em uma Floresta Ombrófila Densa, localizada em Vitória do Jari-AP.

HEG_m (3m)= Hegyi modificado com raio de competição de 3m; HEG_m (5m)= Hegyi modificado com raio de competição de 5m;
HEG_m (10m)= Hegyi modificado com raio de competição de 10m; HEG_m (15m)= Hegyi modificado com raio de competição de  15m e
HEG_m (20m)= Hegyi modificado com raio de competição de 20m; p <0,05.

As maiores correlações com o índice de Hegyi modificado ocorreram com um raio de 20 metros de distância. Onde foi detectada uma correlação forte com a variável DAP (r= -0,697) e uma correlação fraca com a variável de incremento em DAP (r= -0,145) em um raio de 20m. Da mesma forma como ocorreu com o índice de Hegyi sem modificações na fórmula, à medida que a distância do raio aumentava, as correlações ficavam mais altas.

     De forma geral, as correlações dos índices dependentes da distância com a variável DAP (cm) tiveram melhor desempenho em um raio de 20 metros, para ambos os índices e a maior correlação foi de r=-0,697 (correlação forte), para o índice de Hegyi_modificado. A relação destes índices com a variável DAP (cm) indicou uma tendência de aumento de correlação à medida que a distância dos raios aumentava.

 A literatura disponível cita correlações moderadas e fortes, entre a variável DAP e os índices de competição.  No entanto, devemos lembrar que a correlação alta entre o DAP e qualquer índice de competição é devido a relações geométricas e, portanto, não possui nenhuma importância ecológica (Vanclay, 1994).

As correlações dos IDD com a variável ∆DAP foram em grande maioria não significativa estatisticamente e os seus coeficientes de correlação variaram entre r= -0,108 (Índice de Hegyi, com raio= 20m) a r= -0,145 (Índice de Hegyi modificado, com raio= 20m).  A primeira correlação significativa só ocorreu apenas a partir de um raio de 15 m, no índice de Hegyi modificado. Esta relação mostrou haver maiores correlações em raios de competição maiores, porém ainda muito baixas e fracas.

Considerando a análise de todos os índices com a variável ∆DAP, as mesmas foram muito baixas.  As baixas correlações podem ser atribuídas à elevada heterogeneidade de espécies na floresta, idade das árvores e condições gerais de crescimento e sanidade, dentre outros. Castro et al. (2014), em um trabalho em uma floresta natural em Minas Gerais, com 36 espécies mais abundantes, encontrou correlações significativas que variaram de r= 0,22 e r= 0,44, para a mesma variável ∆DAP, porém com distintos índices de competição dependentes da distância. No entanto, quando os autores consideraram a floresta toda, empregando o índice de Hegyi (raio= 6m), encontraram uma correlação de r= 0,12 e neste trabalho este mesmo índice teve uma correlação significativa de r= -0,108, porém com um raio maior (20 m).

Castro et al. (2014), menciona que as correlações dos índices de competição com a variável ∆DAP, foram fracas e em média inferiores a 30%, para o seu estudo em Floresta Estacional Semidecidual Montana com parcela de 1 hectare. Por exemplo, o índice de Hegyi (raio= 6m), resultou em um r= 0,12. Resultados muitos semelhantes ao do presente estudo, onde as correlações não passam de 14,5% (r=-0,145).

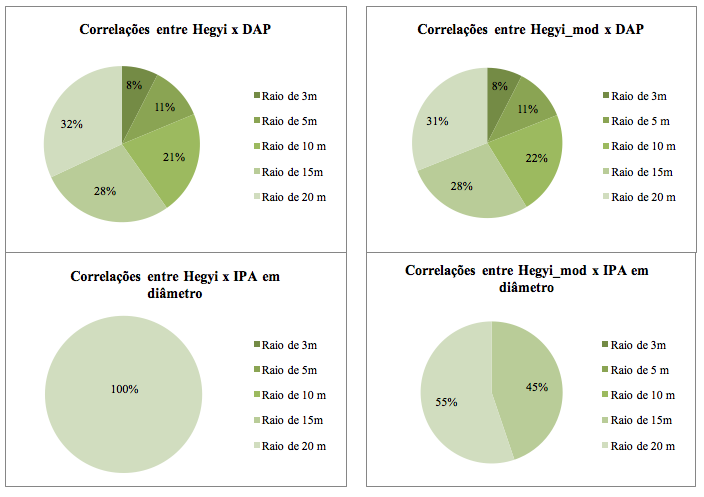
FIGURA 4 – Composição percentual das correlações significativas de cada índice avaliado com as variáveis diâmetro
a 1,30 m de altura (DAP) e incremento em diâmetro (∆DAP) em uma Floresta Ombrófila Densa, localizada em Vitória do Jari-AP.

Nota-se na figura 4, que a relação entre os dois índices de competição dependentes da distância com o DAP, foi muito semelhante. Diferiu apenas ligeiramente nos raios de 10 e de 20 metros.  No entanto, no caso do incremento em diâmetro (IPA), o índice de Hegyi modificado, mostrou ser mais sensível para detectar a competição nesta tipologia florestal, pois o mesmo apresentou correlações em duas distâncias de raios (15 e 20 m), enquanto o índice de Hegyi, em apenas uma (20 m).

     Estes resultados baixos já são esperados em florestas tropicais, pois conforme a pesquisa de Zhao et al. (2006), os efeitos da competição no crescimento das árvores são muito fracos para serem detectado em florestas naturais ricas em espécies. A grande variação no crescimento (altura, diâmetro) em indivíduos do mesmo tamanho, a heterogeneidade de espécies na floresta, idade das árvores e condições gerais de crescimento e sanidade, levam as baixas correlações com a variável ∆DAP (Castro et al., 2014), opinião também defendida por Cunha (2013).

Neste trabalho os índices foram calculados de forma individual, ou seja, para cada árvore e não foram estratificados por espécie. O banco de dados analisado possui 94 espécies, no entanto com representação baixa, com menos de 10 indivíduos por espécie. Apenas 5 espécies apresentam mais do que 10 indivíduos, por esse motivo, não foi realizado a correlação por espécies.

Avaliação dos índices

Os resultados das correlações calculadas entre cada índice e as variáveis da floresta, não se mostraram muito diferentes, e para ambos os IDD testados, as correlações aumentavam à medida que a distância do raio também se elevava.  Essa mesma tendência de maiores correlações em raios maiores, também foi observada por Pukkala e Kolstrom (1987). O raio de competição que apresentou maior correlação com o DAP e  ∆DAP foi o raio de 20 metros.

Apesar de correlações baixas entre os índices de competição e o ∆DAP, Tomé e Burkhart (1989) mencionam que a contribuição dos índices como variáveis em modelos de crescimento é significativa.

Um fato deve ser levado em consideração, quando na justificativa de baixas correlações em florestas tropicais, que são as diferentes interações que cada espécie sofre de forma simultânea com outras árvores.  Por isso, o complexo problema da medição e interpretação de interações bióticas convida a uma série de abordagens, como o aumento do entendimento da competição nas florestas tropicais por meio do desenvolvimento de índices de competição que considerem os conceitos de competição intraespecífica e interespecífica (Castro et al., 2014).

Desta maneira, o estudo empírico dos índices dependentes da distância, parece contribuir parcialmente na descrição dos fatores que interferem na variação do crescimento em florestas naturais. Entretanto, a melhoria destes mecanismos no estudo da competição no crescimento das árvores deve seguir avançando, devendo avaliar as melhores relações com diferentes áreas de competição (raios), bem como, considerar as características genéticas e comportamentais de cada espécie.

5. Conclusão

Os índices avaliados neste trabalho mostraram correlações muito baixas e fracas com as variáveis da floresta, indicando que a competição entre árvores de uma floresta continua sendo de difícil avaliação e medição.

Com este estudo pode-se concluir que:

1. Os índices de competição dependentes da distância apresentam melhores correlações com as variáveis testadas em raios de 15 e 20 metros;
2. O melhor índice foi o de Hegyi modificado, tanto para variável DAP quanto para o ∆DAP, com raio= 20m;
3. Não foi possível detectar um índice de maior superioridade ao outro, no entanto, o índice de Hegyi modificado apresentou ligeiramente melhores correlações para todas as variáveis testadas, indicando ser mais sensível em captar a competição entre as árvores;
4. Os índices de competição dependentes da distância apresentaram melhores correlações com a variável DAP, do que com o ∆DAP;
5. Apesar de baixas correlações, constatou-se potencialidade dos índices de competição como subsídios em estudos de crescimento e produção em nível de árvore individual em Floresta Ombrófila Densa.

O aumento da compreensão dos processos competitivos em uma floresta tropical constitui um desfio para a construção de índices de competição mais eficientes para florestas tropicais.

Referencias

Alder, D. (1995). Growth Modelling for Mixed Tropical Forests. University of Oxford: Tropical Forestry Paper.

Azevedo, C.P. de, Silva, J.N.M., Souza, C. R. de e Sanquetta, C. R. (2012). Eficiência de tratamentos silviculturais por anelamento na floresta do Jari, Amapá. Floresta, 42(2), 315-324.

Béland, M., Lussier, J.M., Bergeron, Y. e Longpré, M.H. (2003). Structure, spatial distribution and competition in mixed jack pine (Pinus banksiana) stands on clay oils of eastern Canada. Ann. For. Sci., 60, 609-617.

Begon, M.; Harper, J.L. e Townsend, C.R. (1996).  Ecology: Individuals, Populations and Communities. Oxford: Blackwell Science.

Berger, U., Piou, C., Schiffers, K. e Grimm, V.  (2008). Competition among plants: Concepts, individual-based modelling approaches, and a proposal for a future research strategy. Perspectives in Plant Ecology, Evolution and Systematics, 9,121–135.

Burkhart, E.H. e Tomé, M. (2012). Modeling Forest Trees and Stands. New York: Springer.

Busing, R.T. e Mailly, D. (2004). Advances in spatial, individual-based modelling of forest dynamics. Journal of Vegetation Science, 15, 831–842.

Castro, R., Soares, C., Leite, H., Souza, A., Martins, F., Nogueira, G., Oliveira, M. e Silva, F. (2014). Competição em nível de árvore individual em uma floresta estacional semidecidual. Silva Lusitana, 22(1), 43-66.

Chassot, T. (2013). Densidade e incremento diamétrico de árvores individuais da floresta ombrófila mista. (Tese de Doutorado). Programa de Pós-graduação em Engenharia Florestal, Universidade Federal de Santa Maria. Santa Maria-RS.

Contreras, M.A., Affleck, D. e Chung, W. (2011). Evaluating tree competition indices as predictors of basal area incremented in western Montana forests. For. Ecol. Manage., 262, 1939-1949.

Cunha, T.A. da . (2013). Competição assimétrica e o incremento diamétrico de árvores individuais de Cedrella odorata L. na Amazônia ocidental. Acta Amazonica, 43(1), 9-18.

Daniels, R.F.  (1976). Notes: simple competition indices and their correlation with annual loblolly pine tree growth. Forest Science, 22(4), 454-456.

Dancey, C. e  Reidy, J. (2006). Estatística Sem Matemática para Psicologia: usando SPSS para Windows. Porto Alegre: Artmed.

Davis, L.S.; Jonhson, K.N.; Bettinger,P. e Howard, T.E. (2005). Forest management: to sustais ecological, economic, and social values. Illinois: Waveland Press.

Deangelis, D.L. e Gross, L.J. (1992). Individual-Based Models and approaches in ecology. New York: Chapman & Hall.

Devore, J.L. (2006). Probabilidade e estatística: para engenharia e ciências. São Paulo: Pioneira Thomson Learning.

Giacomini, H. C. (2007). Os mecanismos de coexistência de espécies como vistos pela teoria ecológica. Oecologia Brasiliensis, 11(4), 521-543.

Gomide, G.L.A. (1997). Estrutura e dinâmica de crescimento de florestas tropicais primárias e secundária no estado do Amapá (Tese de mestrado). Programa de Pós-graduação em Engenharia Florestal, Universidade Federal do Paraná. Curitiba-PR.

Grimm, V. (1999). Ten years of individual-based modelling ind ecology: what have we learned and what could we learn in the future? Ecol. Model. , 115, 129-148.

Hegyi, F.  (1974). A simulation model for managing jack-pine stands. In: Fries, J. (Ed.), Growth Models for Tree and Stand Simulation. Royal College of Forestry, 1974; 74–90.

Hynynen, J. (1995). Predicting tree crown ratio for unthinned and thinned Scots pine stand. Canadian Journal Forest Research, 25, 57-62.

Köppen, W. (1948). Climatologia: con un estudio de los climas de la tierra. México: Fondo de Cultura Econômica.

Liu, J. e Ashton, P.S. (1998). FORMOSAIC: an individual-based spatially explicit model for simulating forest dynamics in landscape mosaics. Ecological Modelling, 106, 177-200.

Lorimer, C. G. (1983). Tests of age-independent competition indices for individual trees in natural hardwood stands. Forest Ecology and Management, 6, 343–360.

Martin, G.L. e Ek, A.R.  (1984). A comparison of competition measures and growth models for predicting plantation red pine diameter and height growth. Forest Science, 30, 731-743.

Martins,  F.B., Soares, C.P.B.,  Leite, H.G., Souza, A.L. de e Castro, R.V.O. (2011). Índices de competição em árvores individuais de eucalipto. Pesquisa agropecuária brasileira, 46(9), 1089-1098.

Miina, J. e Pukkala, T.  (2002). Application of ecological field theory in distance-dependent growth modelling. Forest Ecology and Management, 161, 101-107.

Odum, E.P. e Barrett, G.W. (2007).  Fundamentos da ecologia. São Paulo: Thompson Learning.

Pedersen, R.O., Naesset. E., Gobakken, T. e Bollandsas, O.M. (2013). On the evaluation of competition indices: the problem of overlapping samples. Forest Ecology and Management, 310, 120-133.

Peng, C. (2000). Growth and yield models for uneven-aged stands: past, present and future. Forest Ecology Management, 132, 259-279.

Pretzsch, H. (2009). Forest dynamics, growth and yield: from measurement to model. Berlin: Springer-Verlag.

Prodan, M.; Peters, R.; Cox, F. e Real, P. (1997). Mensura Florestal. San José: GTZ/IICA.

Pukkala, T. e  Kolstrom, T. (1987).  Competition indices and the prediction of radial growth in Scots pine. Silva Fennica, 21, 55-67.

Pukkala, T. (1989).  Methods to describe the competition process in a tree stand. Scandinavian Journal of Forest Research, 4, 187-202.

Roitman, I.  (2011). Modelagem espacial e temporal na mata de galeria do gama- DF.  (Tese de Doutorado). Programa de Pós-graduação em Ecologia, Universidade Federal de Brasília. Brasília-DF.

Schneider, P. R. e Schneider, P. S. P. (2008). Introdução ao manejo florestal. Santa Maria: UFSM, FACOS.

Tomé, M., Burkhart, H.E. (1989). Distance-dependent competition measures for predicting growth of individual trees. Forest Science, 35, 816-831.

Triola, M.F. (2005). Introdução à estatística. Rio de Janeiro: LTC.

Vanclay, J.K. (1994). Modelling Forest Growth and Yield. Applications to Mixed Tropical Forests. Guilford: CAB International/Briddles.

Vanclay, J. K. (2006). Spatially-explicit competition indices and the analysis of mixed-species plantings with the Simile modelling environment. Forest Ecology and Management, 23, 295–302.

Veloso, H.P., Rangel Filho, A.L.R. e Lima, J.C.A. (1991). Classificação da vegetação brasileira adaptada a um sistema universal. Rio de Janeiro: IBGE, Departamento de recursos naturais e estudos ambientais.

Weiskittel, A.R.; Hann, D.W.; Kershaw, J.R. e Vanclay, J.K. (2011).  Forest Growth and Yield Modeling. Chichester: Wiley-Blackwell.

Welden, C.W. e Slauson, W.L.  (1986). The intensity of competition versus its importance: an overlooked distinction and some implications. Quarterly Review of Biology, 61, 23–44.

Wykoff, W.R.  (1990). A basal area increment model for individual Conifers in the Northern Rocky Mountains. Forest Science, 36, 1077–1104.

Zhao, D., Borders, B., Wilson, M. e Rathbun, S.L. ( 2006). Modeling neighborhood effects on the growth and survival of individual trees in a natural temperate species rich forest. Ecological Modelling, 6(1), 90-102.

1. Doutoranda em Ciências Florestais pela Universidade Federal Rural da Amazônia, Belém-PA, Brasil. Email: vetraz@yahoo.com.br
2. Doutor em Ciências Florestais pela Universidade de Oxford, Oxford, Reino Unido.
3. Doutor em Ciências Florestais pela Universidade de Oxford e Professor na Universidade Federal Rural da Amazônia, Belém-PA, Brasil.