HOME | ÍNDICE POR TÍTULO | NORMAS PUBLICACIÓN

Espacios. Vol. 37 (Nº 13) Año 2016. Pág. 22

Classificação da similaridade dos cursos de graduação da UFSM em relação ao índice do aluno equivalente – Uma ferramenta de gestão

Classification of the similarity of the undergraduate courses of UFSM compared to the index of the student equivalent – A management tool

Jean Cauê HUPPES 1; Adriano Mendonça SOUZA 2; Angela Pelgrin ANSUJ 3

Recibido: 27/01/16 • Aprobado: 04/03/2016

Contenido

1. Introdução

2. Materiais e métodos

3. Resultados

4. Conclusão

Bibliografia

1. Introdução

As Instituições Federais de Ensino Superior (IFES), especialmente as criadas na década de 60, organizaram-se sob a forma de autarquia de regime especial, o que significa fazer parte da administração pública, portanto sendo submetida às legislações que regem as demais organizações federais (SANTOS, 2013). Segundo o mesmo autor, no início da década de 90, o conjunto do sistema de ensino superior no país era constituído por 918 instituições, sendo 222 de natureza pública (federais, estaduais e municipais). Vinte anos depois, segundo dados do Censo de Educação Superior, 2010, realizado pelo Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira – INEP, esse sistema já contava com 2.378 instituições de ensino superior, sendo que apenas 278 pertenciam ao segmento público (Federais: 99, Estaduais: 108 e Municipais: 71), enquanto 2.100 pertenciam ao setor privado.

Perante este cenário surge à necessidade de financiamento destas instituições onde em 1920 se iniciou com a Universidade do Rio de Janeiro, transformada na Universidade do Brasil, em 1937, e na Universidade Federal do Rio de Janeiro (UFRJ), a partir de 1965 (AMARAL, 2008).

Assim, diante do crescente número de instituições públicas tornou-se necessário a criação de critérios para alocação desses recursos, tanto para os cursos de graduação, mestrado strictu senso, doutorado e residência médica. Com isso, iniciou-se a criação de índices formados por diversas variáveis.

Sendo que o índice denominado aluno equivalente é o principal indicador para a análise dos custos de manutenção e desenvolvimento das IFES nas categorias econômicas Capital e Despesas Correntes, financiados com recusos do fundo público federal (BRASIL, 2005). O cálculo deste indicador foi inspirado no modelo inglês de 1998, elaborado pelo Higher Education Council for England (HEFCE), utilizado na Inglatera até o ano de 2004 quando sofreu alterações e foi objeto de estudos realizados pela Secretaria de Educação Superior (SESu)/MEC e pela Associação Nacional dos Dirigentes das Instituições Federais de Ensino Superior (Andifes). Inclui-se no cálculo todos os cursos de caráter permanente que não sejam autofinanciados, mantidos por recursos especiais de convênios ou em parcerias com instituições públicas ou privadas.

Em 1968, durante o período militar, o ensino superior brasileiro passa por mudanças, através da Lei nº 5.540/1968, denominando-se reforma universitária. Segundo Duenhas (2013, p. 42), tal reforma "trouxe uma nova configuração para o nível de ensino terciário e esta lei teve impacto nas instituições públicas e privadas".

As diretrizes básicas e os critérios para distribuição de recursos orçamentários nas Universidades Federais foram estabelecidos por meio do decreto presidencial nº 7.233, de 19 de julho de 2010 que "dispõe sobre procedimentos orçamentários e financeiros relacionados à autonomia Universitária" (BRASIL, 2010). Com o intuito de institucionalizar a alocação dos recursos de custeio e capital de forma a garantir precisão técnica e transparência na distribuição desses recursos, o decreto estabelece diretrizes e indicadores de qualidade e produtividade, denominada Matriz Andifes. Desse modo, a universidade deve apresentar um desempenho e produtividade satisfatórios que são monstrados em seus indicadores, para fins de alocação e uso eficiente de recursos humanos e financeiros. O Ministério da Educação e Cultura- MEC- determina separadamente o volume de recursos para a manutenção, investimentos e para pessoal.

Em relação ao Orçamento Básico, a parcela de Manutenção não utiliza um modelo de partição. Ela é calculada utilizando-se a Unidade Básica de Custeio - UBC- multiplicada pelo número de alunos equivalentes (Nfte) de cada IFES, o que corresponde 80% do valor total do Orçamento de Manutenção. A segunda parcela denominada parcela de Qualidade e Produtividade utiliza um modelo de partição que considera indicadores qualitativos. Segundo Silva (2011, p. 73) "esta parcela deveria manter a política de aperfeiçoamento qualitativo e quantitativo, buscando manter a competitividade das IFES".

Para o cálculo da UBC foi utilizado o número total de alunos equivalentes do sistema, dividido pela soma total de Outros Custeios e Capital – OCC- comprometida com os 12 itens de manutenção básica (combustíveis e lubrificantes; locação de imóveis; locação e manutenção de equipamentos; água e esgoto; serviços de comunicação; cópias e reprodução de documentos; energia elétrica; telecomunicações; serviços de limpeza; serviços de vigilância e portaria; diárias; e passagens) por todas as IFES. O orçamento de cada universidade é definido ao multiplicar o total de seus alunos equivalente- Nfte- pelo valor da UBC calculada.

O conceito de aluno equivalente busca retratar a quantidade total de alunos matriculados em cada IFES, com base em cálculo que equipara aos alunos dos cursos a variáveis, como: nível de custos, tempo previsto de duração dos cursos e eficiência na formação dos ingressantes, o cálculo do Número de Alunos Equivalente total –Nfte- pode ser visto em (BRASIL/MEC, 2005).

Para tanto, é utilizado um modelo matemático específico que inclui várias constantes e distintas variáveis que  possibilita chegar a um total de alunos que sirva de comparação para todos os cursos em todas as IFES objeto do cálculo (BRASIL/MEC, 2005).

O problema da pesquisa reside em analisar o Nfte de 8 centros de Ensino da UFSM de maneira simultânea considerando-se que existem 60 cursos de graduação analisados durante 4 anos utilizando-se a análise de cluster, o que em uma única análise é capaz de classificar e identificar os cursos em relação as variáveis analisadas

Tem-se como objetivo classificar os cursos que apresentam menor e maior contribuição em relação ao Nfte(G) de oito centros de Ensino da UFSM no período de 2010 à 2013 e identificar a variável que possa sofrer alterações para melhorar o Nfte(G) do curso em cenários otimistas com aumentos de 20, 40 e 60% de modo a auxiliar os gestores na captação de recursos.

2. Materiais e métodos

A realização desta pesquisa deu-se a partir de um levantamento bibliográfico sobre os principais assuntos relacionado ao índice aluno equivalente. As principais fontes de pesquisa foram artigos nacionais, dissertações e teses relacionadas ao assunto e documentos oficiais do Ministério da Educação.

O estudo envolveu os 60 cursos de graduação, nos 8 Centros de Ensino, que se enquadram no índice aluno equivalente de graduação Nfte(G), no período de 2010 à 2013, da Universidade Federal de Santa Maria (UFSM) coletados no  Centro de Processamento de Dados (CPD) da UFSM.

Os cursos foram agrupados em oito centros de ensino como apresentados a seguir: CAL - Centro de Artes e Letras (10 cursos selecionados): DIV - Desenho Industrial - Programação Visual; ACD - Artes Cênicas – Direção teatral, AVB - Artes Visuais- Bacharelado em Desenho e Plástica, AVL - Artes Visuais Licenciatura, ML - Música Licenciatura, LPL – Letras (Licenciatura) - Português e Literaturas de Língua Portuguesa, LI – Letras (Licenciatura) - Português e Literaturas de Língua Inglesa, LE- Letras (Licenciatura) - Português e Literaturas de Língua Espanhola, DIP- Desenho Industrial – Projeto de Produto, MBV – Música Bacharelado - Violão. CE- Centro de Educação (4 cursos selecionados): PN – Pedagogia Noturno, PD – Pedagogia Diurno, EES – Educação Especial, PE – Programa Especial de Educação. CCSH – Centro de Ciências Sociais e Humanas (16 cursos selecionados): FL – Filosofia, H – História Licenciatura/Bacharelado, AD – Administração Diurno, CCN – Ciências Contábeis Noturno, DD – Direito Diurno, CEN – Ciências Econômicas Noturno, CJ – Comunicação Social – Habilitação Jornalismo, CPP - Comunicação Social – Habilitação Publicidade e Propaganda, CRP - Comunicação Social – Habilitação Relações Públicas, AR – Arquivologia, AN – Administração Noturno, DN – Direito Noturno, P – Psicologia, CED – Ciências Econômicas Diurno, CSB – Ciências Sociais Bacharelado, CCD – Ciências Contábeis Diurno. CCS – Centro de Ciências da Saúde (6 cursos selecionados): M- Medicina, O - Odontologia, FO - Fonoaudiologia, E- Enfermagem, FI - Fisioterapia, F- Farmácia. CCR – Centro de Ciências Rurais (4 cursos selecionados): A – Agronomia, EF – Engenharia Florestal, Z – Zootecnia, MV- Medicina Veterinária. CCNE - Centro de Ciências Naturais e Exatas (12 cursos selecionados): QL – Química Licenciatura, QI – Química Industrial, CB – Ciências Biológicas, GL – Geografia Licenciatura, GB – Geografia Bacharelado, FB – Física Bacharelado, MLN – Matemática Licenciatura Noturno, FLN – Física Licenciatura Noturno, ME – Meteorologia, MLB – Matemática Núcleo Comum, MLD – Matemática Licenciatura Diurno, QB – Química Bacharelado. CEFD – Centro de Educação Física e Desportos(2 cursos selecionados): EFL – Educação Física Licenciatura, EFB – Educação Física Bacharelado. CT – Centro de Tecnologia (6 cursos selecionados): EC – Engenharia Civil, EE – Engenharia Elétrica, EM – Engenharia Mecânica e  EQ – Engenharia Química, C – Computação, ART – Arquitetura.

As variáveis utilizadas para a construção do índice foram: Duração média dos cursos (D), número de diplomados (Ndi), número de matriculados (Ni), peso do grupo (PG), fator de retenção (R), bônus por turno (BT) e bônus fora de sede (BFS).

Segundo Brasil (2005), o cálculo do índice Aluno Equivalente de graduação é subdividido em três grupos; Cursos de tempo integral de acordo com a  equação  (1).

Nfte(G)={[Ndi.D.(1+R)]+[(Ni-Ndi)/4] .D}. BT. BFS.PG                        (1)

Para cursos novos e para cursos intervalados com Ndi=Ni=zero aplica-se a equação (2).

Nfte(G)= NMR. BT. BFS. PG                                                        (2)

Onde NMR é o número de alunos matriculados no ano de referência do cálculo e, para cursos que não apresentam ingressantes (Ni=zero) ou para cursos que apresentam o número de ingressantes menor que o número de diplomados (Ni<Ndi), a segunda parcela da equação (3) torna-se zero.

 Nfte(G)= [Ndi. D. (1+R)]. BT. BFS. PG                                       (3)

Os dados serão analisados de forma quantitativa, utilizando-se a análise descritiva como média, desvio padrão, coeficiente de variação e medidas separatrizes como os quartis. A média aritmética quando analisada isoladamente, pode ser insuficiente, mas, a utilização da medida do desvio padrão que é uma medida de dispersão, mede o grau de afastamento dos valores de um conjunto de dados em relação ao valore médio. Todavia, o desvio padrão é que indica quantas unidades variam para cima ou para baixo da média.

Para verificar a qualidade das médias é necessário calcular o coeficiente de variação, que é o desvio padrão dividido pela média vezes 100, o qual é expresso em percentuais. Esse valor deve estar abaixo de 50%, mostra assim, que a média é representativa do conjunto de dados. A média, o desvio padrão e o coeficiente de variação são medidas descritivas univariada, isto é, quando aplicadas, analisam individualmente o conjunto de dados sem levar em consideração quaisquer relação.

Com o intuito de separar os cursos em mais similares e menos similares, lança-se mão da técnica de análise de cluster, pois baseando-se nas variáveis utilizadas, busca-se identificar quais cursos possuem um maior e/ou menor Nfte(G) e consequentemente uma maior ou menor aporte de recursos. Esta técnica se justifica dado ao grande número de cursos envolvido e o número de variáveis e apenas com a medida de  distâncias e o método de aglomeração adequado é possível classificar  os cursos. A análise de cluster, segundo Hair (2005, p 384), Malhorta (2001, p 526), será utilizada para agrupar os cursos que apresentam maior e menor desempenho em relação ao índice Nfte(G). De acordo com Souza (2011), a análise de cluster é utilizada para classificar objetos ou casos em grupos relativamente homogêneos. Os clusters devem apresentar uma grande homogeneidade interna (dentro do grupo) e heterogeneidade externa (entre os grupos), sendo semelhantes entre si, se diferenciando dos demais. Segundo Souza e Vicini (2005) a análise de cluster pode ser organizada baseando-se no cálculo das distâncias euclidianas entre os objetos identificados no espaço multiplano de todas as variáveis consideradas, logo, a distância euclidiana pode ser calculada com a fórmula e seus respectivos pares de coordenadas de pontos quaisquer do plano. Uma vez que os objetos encontram-se ligados pela menor distância, é necessário definir igualmente a noção de distância entre os grupos de objetos, ou individualmente, entre um objeto e um grupo. Os métodos mais usuais são: a inserção pelo vizinho mais próximo, a inserção pelo vizinho mais distante e a inserção pela distância média. Subsequente a esses procedimentos identifica-se a coerência de grupos dentro do universo de objetos estudados e realizam-se as análises através de um pacote estatístico.

 Determinados os processos de cálculo das distâncias deve-se utilizar os métodos de aglomeração. Segundo Souza e Vicini (2005), os métodos aglomerativos ou métodos de aglomeração são as formas em que cada elemento será aglutinado a um determinado cluster, os métodos de aglomeração, dividem-se em métodos de encadeamento, métodos de variância e métodos de centróide. Nesta pesquisa será utilizado o método da regra do vizinho mais próximo (Single Linkage), onde a distância entre o grupo formado e um outro é igual à menor das distâncias entre os elementos dos dois grupos.

Identificados os cursos mais similares e serão investigadas as variáveis que compõem o Nfte(G) dos seis cursos com menor desempenho e os seis cursos com maior desempenho, com o intuito de verificar qual variável pode ser aprimorada para fornecer um melhor aporte de recursos via Nfte. A escolha dos seis cursos é arbitrária, pois corresponde apenas a 10% dos cursos mais similares e dos menos similares, desta forma é possível verificar o comportamento dos cursos com maior Nfte(G) e com menor Nfte(G).

Após identificados os 10% dos extremos em termos de Nfte(G), passa-se a identificação das as variáveis que compõem o Nfte(G) e que podem ser melhoradas pelo desempenho do gestor. Estas variáveis sofrerão um incremento de 20, 40 e 60% respectivamente de modo a formar cenários para verificar o seu comportamento em relação ao Nfte(G) proporcionando cenários otimistas que possibilitem galgar maiores recursos orçamentários para os cursos e subsidiar os gestores dos cursos com tomadas de decisões e iniciativas para um maior aporte de Nfte.

3. Resultados

Serão apresentados os resultados da estatística descritiva que busca caracterizar cada curso individualmente e posteriormente aplica-se a análise de cluster para se ter uma visão conjunta do comportamento dos cursos entre si.

3.1. Estatística descritiva

O índice Nfte(G) de cada Instituição Federal de Ensino Superior -IFES- é elaborado com o somatório do Nfte(G) de cada curso. A média, desvio padrão, coeficiente de variação, valores máximos e mínimos foram calculados com os dados dos índices por ano, no período de 2010 à 2013 de 60 cursos de graduação, totalizando 240 observações.

No ano de 2010 a média do índice Nfte(G) foi de 326,35, com desvio padrão de 536,57, coeficiente de variação de 164,42% com o valor máximo de 3044,52 e valor mínimo de 6,34. No ano de 2011 a média do índice Nfte(G) foi de 335,34, com um desvio padrão de 541,83, coeficiente de variação de 161,58% com valor máximo de 2947,99 e valor mínimo de 4,35. No ano de 2012 a média do índice Nfte(G) foi de 322,98, com um desvio padrão de 533,04, coeficiente de variação de 165,09% com valor máximo de 3096,76 e valor mínimo de 4,66. No ano de 2013 a média do índice Nfte(G) foi de 330,16, com um desvio padrão de 537,12, coeficiente de variação de 1,63% com valor máximo de 2986,74 e valor mínimo de 5,21.

A média dos 60 cursos dos 4 anos foi de 328,7, com um desvio padrão de 51,4, com valor máximo de 3019,005 e valor mínimo de 5,14. A média do índice Nfte(G) dos 60 cursos de graduação foi subdividido em três medidas separatrizes, primeiro quartil=104,67, segundo quartil ou mediana=139,01 e terceiro quartil=240,99.  

Os três cursos que apresentaram maior variabilidade entre eles foram artes cênicas – direção teatral, matemática núcleo comum e matemática licenciatura diurno.

Os cursos com maior índice médio Nfte(G), pertencentes ao terceiro quartil são respectivamente: Medicina (M), Medicina Veterinária (MV), Odontologia (O), Zootecnia (Z), Agronomia (A) e Farmácia (F), como pode ser visto na Tabela 1.          

Tabela 1: Cursos com maior média do índice Nfte(G) no período de 2010 à 2013

Na Tabela 2 estão localizados os cursos com menor média Nfte(G) dos 4 anos pesquisados. Dos 6 cursos com menor Nfte(G), 2 cursos não são representativos – ACD e MLB- pois tem um coeficiente maior que 50%.

Tabela 2 – Cursos com menor índice Nfte(G) no período de 2010 à 2013

Esta análise descritiva mostra o comportamento dos cursos em termos de Nfte durante os quatro anos em análise de forma individualizada, mas busca-se agora analisar o comportamento conjunto destes cursos.

3.2. Análise de Cluster

A Figura 1 mostra o cluster utilizando a média do índice Nfte(G), por ano, dos 60 cursos.

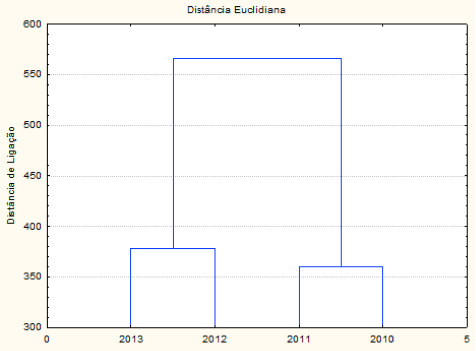
Figura 1 - Cluster da média do índice Nfte dos 60 cursos analisados de 2010 à 2013.

Pela Figura 1 verifica-se o comportamento da média do índice Nfte(G) ao longo dos 4 anos analisados, que 2013 e 2012 possuem um comportamento similar, concomitantemente aos anos 2011 e 2010. Pela análise descritiva verifica-se que o índice Nfte(G) de 2013 e 2012 apresentam comportamento similar devido ao fato de existir pouca variação, assim como nos anos de 2011 a 2010. Vale ressaltar que na análise dos clusters foram utilizados os Nfte(G) de cada curso no período de 4 anos, desta forma quando se realiza a análise descritiva utilizando a média e o desvio padrão, pode haver uma influência no valor da média por valores extremos. Uma outra observação que deve ser feita é que quando se traça o dendrograma, calcula-se a distância de cada uma das variáveis em relação aos anos e é possível dizer que os anos de 2011 e 2012 foram similares em termos de Nfte(G) e que os anos de 2012 e 2013 embora similares são diferentes de 2010 e 2011. O que se busca é verificar como estes cursos se comportaram em relação a estes quatro anos.

A Figura 2, mostra o agrupamento de 60 cursos de graduação, utilizando o Nfte(G) dos 4 anos coletados.

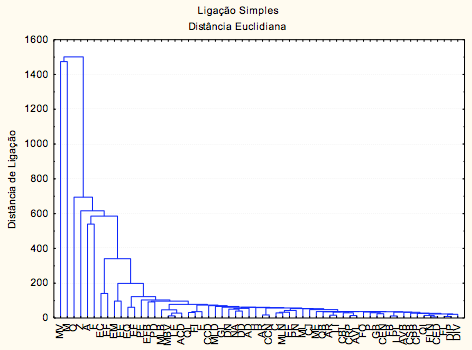
Figura 2 - Cluster do Nfte(G) dos 60 cursos analisados do período de 2010 à 2013.

Observa-se na Figura 2 que os 6 cursos mais discrepantes dos demais são: medicina, medicina veterinária, odontologia, zootecnia, agronomia e farmácia, são considerados discrepantes, pois possuem maior distância de ligação, isto é, MV e M, possuem uma distância de ligação acima de 1400 observado no eixo Y da Figura 2. Os cursos mais similares, isto é, que possuem menor distância de ligação, estão melhor representados na Figura 3 que são ciências econômicas diurno, física licenciatura noturno, filosofia, desenho industrial – projeto de produto, química industrial e desenho industrial – programação visual em relação aos demais.

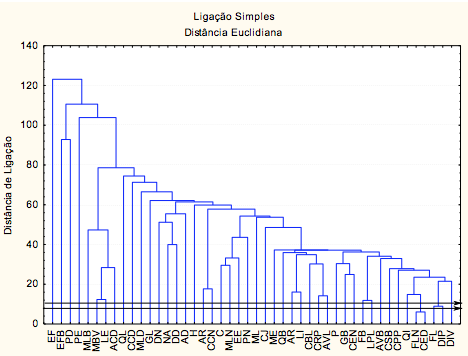
Figura 3 – Cluster formado por 46 cursos de graduação mais discrepantes

Analisam-se as medidas descritivas no intuito de identificar as variáveis de maior contribuição. A média dos seis cursos que mais contribuem para a elaboração do índice Nfte(G) sequencialmente são, M, MV, O, Z, A e F como pode ser constatado na Tabela 1, que foi construída com base nos 6 primeiros cursos que pertencem ao primeiro quartil das médias do Nfte(G). Concomitantemente pode-se constatar ao observar na Figura 2, a mesma constatação com os grupos discrepantes, ou seja, duplas de cursos que formam um grupo com maior distância euclidiana entre si.

Ao analisar a Figura 3, observa-se melhor as duplas de cursos com menor distância euclidiana, ou seja, grupo de pares mais similares. Os seis cursos com o Nfte(G) mais similares, no período de 4 anos subsequentemente, encontram-se nos seguintes cursos respectivamente com as distâncias entre si: Ciências Econômicas Diurno (CED) e Física Licenciatura Noturno (FLN) com distância euclidiana igual a 6. Filosofia (FL) e Desenho Industrial – Projeto de Produto (DIP) com distância euclidiana igual a 9 e em terceiro lugar o curso com menor distância euclidiana entre os pares é Letras Espanhol (LE) e Música Bacharelado Violão (MBV) com distância euclidiana igual a 12.

Ao observar a Tabela 2 com as variáveis que formam o Nfte(G), compostas pelas médias aritméticas, no período de 4 anos, organizadas em ordem decrescente pela média do Nfte(G), constata-se que 6 cursos estão localizados no terceiro quartil, isto é, os cursos com menor Nfte(G) são: LE, MBV, ACD, MLB, ML e AR.

Nesta análise foi possível identificar que a variável Ndi foi a que influenciou diretamente no cálculo do Nfte(G). Constatou-se o número de diplomados (Ndi) pode sofrer intervenções e ações pedagógicas específicas para cada curso de modo que ocorram incrementos de forma a melhorar o Nfte(G).

A discrepância em termos de aporte de Nfte(G) possibilitou selecionar cursos com cenários otimistas para uma investigação futura, com base nas medidas implementadas pelos gestores. O número de diplomados e o número de ingressantes são as duas variáveis que podem a curto prazo modificar o cenário pré analisado na matriz de distribuição ANDIFES. O número de ingressantes é em geral fixo, pois são as vagas oferecidas que geralmente são preenchidas. Desta forma, modifica-se primeiramente o Ndi(G) apresentado na Tabela (3) com alterações de 20, 40 e 60%.

Tabela 3 – Cursos com menores médias Nfte(G) no período de 2010 à 2013

Ao analisar o curso com menor índice Nfte(G), Letras Espanhol (LE) por exemplo, com a média aritmética elaborada no período de 2010 à 2013, Nfte(G) = 5,14, pode-se constatar na Tabela 3 uma possível previsão ao aumentar o número de diplomados (Ndi) em 20, 40 e 60%. Respectivamente o Nfte(G) passará de 5,14 com um aumento de 20% no Ndi (de 8,75 para 10,5), acarretará num Nfte(G)=5,67 resultando um aumento de aproximadamente 10%. Diretamente proporcional ao aumentar a variável Ndi, aumentará a variável Nfte(G), salienta-se que o aumento do número de diplomados tem um limite a ser cuidado, pois existem cursos como o de medicina que o número de formados é quase igual o número de ingressantes, não possibilitando incrementos de 20, 40 e 60% no Ndi. Quando o número de ingressantes foi igual a zero ou menor que o número de diplomados, aplica-se a fórmula (3), neste caso, dentre os cursos de menor Nfte, dois deles aplicam-se a fórmula (3), MBV e ACD. Nestes dois cursos se aumentar 20% o Ndi de  1,5 para 1,8 e 2 para 2,4, os Nfte(G) aumentará aproximadamente 20% o Nfte(G). Se nos dois cursos aumentar o número de diplomados em 40 e 60%, terá um aumento no Nfte(G) diretamente proporcional.

4. Conclusão

Este estudo objetivou analisar as variáveis que compõe o principal índice de alocação de recursos financeiros das IFES. Para efetivar com sucesso a autonomia orçamentária das IFES, é necessário para o gestor público utilizar ferramentas quantitativas eficazes. Nesta pesquisa, apresenta-se duas ferramentas estatísticas importantes, análise descritiva e a análise de agrupamento ou análise de cluster. Ná primeira análise pode-se concluir no conjunto de 240 observações organizados com o índice de aluno equivalente de graduação – Nfte(G)- de 60 cursos da UFSM coletados no período de 2010 à 2013.

Com a primeira análise de cluster, pode-se observar o grau de similaridade entre os 4 anos com os 60 cursos. Ao comparar com os dados descritivos dos respectivos anos, constatou-se que a distância entre os anos 2013 e 2012 possuem um comportamento similar, concomitantemente aos anos 2011 e 2010. Pela análise descritiva verifica-se que o índice Nfte(G) de 2013 e 2012 apresentam comportamento similar devido ao fato de existir pouca variação, assim como nos anos de 2011 a 2010.

Na segunda análise, constatou-se que os cursos com menor distância apresentados na Figura 3, nesta ordem, são: FLN, CED, FL, DIP, MBV e LE, pode-se constatar também que a menor distância euclidiana entre os índices de cada curso, não significa que estes cursos são os de menor orçamento ou menor índice Nfte(G), como pode ser visto na Tabela 2 construída a partir da média das variáveis que compõem o Nfte(G) dos 4 anos pesquisados. Os cursos com menor índice Nfte(G) são nesta ordem, LE, MBV, ACD, MLB, ML e AR. Ao comparar a média do Nfte(G) do curso que mais contribui (M = 3019) com o curso que menos contribui (CED = 108) constata-se uma diferença de quase 28 vezes.

Na terceira e última análise, foi identificado o fator de maior impacto na elaboração do índice aluno equivalente de graduação – Nfte(G)- que deve ser avaliado cuidadosamente na tomada de decisão do gestor público das IFES, visto que tal ferramenta estatística (Cluster) identifica os cursos que devem ser priorizados na decisão e repasses orçamentários e que o gestor deve tomar medidas de modo que exista um aumento de número de formados nestes cursos, implementando medidas didáticas ou de incentivo específicas para cada curso de modo a baixar o número de retenção e/ou desistência dos alunos.

A análise descritiva focou diretamente no índice do Nfte(G), identificado por meio dos quartis os cursos com maior e menor aporte nestes índices, já análise de cluster buscou identificar os comportamentos similares entre os cursos, baseando-se nas sete variáveis originais dos sessenta cursos de graduação durante os quatro anos. Esta análise de cluster foi importante porque forneceu uma medida que englobou todas as variáveis simultaneamente. O fato de alguns cursos identificados com maior e menor Nfte(G) pelos quartis serem os mesmos que os identificados pela análise de cluster, mostra que pela análise de cluster, o gestor terá melhor subsídios na identificação das variáveis originais que mantiveram os cursos semelhantes próximos, onde foi possível identificar que a variável Ndi é a variável que impacta diretamente neste índice, e que pode ser melhorada pelo gestor.

Deixa-se como sugestão para estudos futuros a aplicação da análise de cluster de modo a se ter uma outra visão sobre o problema proposto.

Bibliografia

AMARAL, N. C.(2008) Autonomia e financiamento das IFES: Desafios e ações. Campinas; Sorocaba, SP. v. 13, n.3, p. 647-680.

BRASIL (2005). Ministério da Educação. Definição de variáveis. Conceituação dos dados utilizados para distribuição de recursos para as IFES. Disponível em: http://pingifes.mec.gov.br/pingifes/index.php?option=com_docman&Itemid=36

BRASIL (2010). Ministério da Educação. DECRETO Nº 7.233, DE 19 DE JULHO DE 2010. Disponível em: https://www.planalto.gov.br/ccivil_03/_ato2007-2010/2010/decreto/d7233.htm

DUENHAS, R. A. O (2013) compartilhamento do financiamento das instituições públicas de ensino superior: Análise empírica utilizando os microdados do INEP. 2013. 156f. Tese (Doutorado em Desenvolvimento Econômico). Universidade Federal do Paraná, Curitiba.

GIL, Antônio Carlos.(2007) Como elaborar projetos de pesquisa. São Paulo: Atlas.

HAIR, J. F., et al.(2005) Análise multivariada de dados. Trad. Adonai S. Sant'Anna e Anselmo C. Neto. 5 ed. Porto Alegre: Bookman.

KENDALL, M.G. (1957) A course in multivariate analysis. London: Griffin.

MACEDO, S.G. (2001) Desempenho Docente pela Avaliação Discente: Uma proposta metodológica para subsidiar a gestão universitária. Florianópolis: UFSC, 2001, 131 p. Tese (Doutorado em Engenharia de Produção) – Universidade Federal de Santa Catarina.

MALHOTRA, N. (2006) Pesquisa de marketing: uma orientação aplicada. Trad. Laura Bocco. 4 ed. Porto Alegre: Bookman.

PEREIRA, J.C.R. (2001) Análise de Dados Qualitativos: Estratégias metodológicas para as ciências da saúde, humanas e sociais. 3. Ed. ; São Paulo: USP.

SANTOS, F. S. dos. (2013) Financiamento público das instituições federais de ensino superior - IFES: Um estudo da Universidade de Brasília - UnB.  XII, 69 f. Dissertação (Mestrado Profissional em Economia)—Universidade de Brasília, Brasília.

SILVA, A. C. L. da. (2011) A análise de estratégias de desenvolvimento acadêmico da UFSCar e suas implicações para a distribuição de recursos do MEC- São Carlos: UFSCar.

SOUZA, A. M.; Schmidt, A.S.;Turcato, C.R. da S..(2011) O aprendizado em organizações certificadas pela NBR ISSO 9001:2000. Revista Online. Florianópolis, SC, v11, n.2, p. 289-318.

SOUZA, A. M.; Vicini, L. (2005) Análise multivariada da teoria a prática. Santa Maria: Departamento de Estatística UFSM.

1. Licenciado em Matemática pela Universidade Federal de Santa Maria e estudante de mestrado no Programa de Pós Graduação em Engenharia de Produção da Universidade Federal de Santa Maria.
2. Professor associado do Departamento de Estatística e atua no Programa de Pós Graduação em Engenharia de Produção da Universidade Federal de Santa Maria.
3. Professora associada do Departamento de Estatística da Universidade Federal de Santa Maria.