HOME | ÍNDICE POR TÍTULO | NORMAS PUBLICACIÓN

Espacios. Vol. 37 (Nº 07) Año 2016. Pág. 14

Previsão da produção mundial de arroz

Forecast of world rice production

Letícia MARASCA 1, Adriano Mendonça de SOUZA

Recibido: 28/10/15 • Aprobado: 25/11/15

Contenido

1. Introdução

2. Modelos de Séries Temporais

3. Metodologia

4. Aplicações e Discussão

5. Conclusões

Referências

1. Introdução

Dentre os cereais produzidos e consumidos mundialmente, temos o arroz como o grão de maior poder nutritivo, cereal balanceado e responsável por 20% da energia e 15% das proteínas necessárias ao nosso organismo. Esse cereal é a base da alimentação humana, responsável pela metade da energia e proteínas necessárias ao desenvolvimento do indivíduo. É um cereal presente em todos os continentes, tanto seu cultivo como na alimentação dos consumidores. Do cultivo ao consumo, este grão destaca-se no cenário econômico e social de diversas famílias, sendo este ciclo como um dos mais importantes para o agronegócio brasileiro (Vieira et al., 2012).

Como característica importante em seu cultivo, o arroz é um cereal que apresenta boa adaptação às várias condições de clima e solo, possuindo, com isso, um enorme potencial para um grande aumento de sua produção, se tornando o cereal mais propenso a sanar a fome do mundo.

Neste cenário, o Brasil apresenta um importante papel, como maior produtor de arroz da América Latina, e ocupa o 9º lugar na produção mundial, sendo apontado como o primeiro país a cultivar o cereal no continente americano. A produção de arroz no Brasil deve se estabilizar em 12.628,2 mil toneladas, com um incremento de 967,3 mil toneladas, (8,3%) em relação à safra 2009/10, que foi de 11.660,9 mil toneladas (Conab, 2012).

Devido à sua enorme importância, tanto no âmbito nacional quanto mundial, este tem como objetivo prever a produção mundial de arroz, por meio da metodologia Box & Jenkins.

Este artigo está organizado da seguinte forma: o item 2 contém a revisão de séries temporais. O item 3 apresenta a metodologia. O item 4 contém as aplicações e discussões, e por fim, no item 5, as conclusões.

2. Modelos de Séries Temporais

As observações correlacionadas entre si e que seguem uma ordem cronológica, com dados equidistantes, chamamos de séries temporais. O estudo das séries temporais nos propicia conhecer o processo gerador da série e analisar os componentes que fazem parte dela. Para conhecer os componentes da série temporal é necessária a sua decomposição (Russo, Ilgner & Basso, 2015).

Para aplicação da maioria dos modelos estatísticos nas séries temporais, estas devem ser estacionárias. A estacionariedade numa série temporal nos diz que os dados que compõem essa série oscilam numa média constante, se mantendo estáveis durante seu período de análise e a estacionaridade de 2ª ordem é quando os dois principais momentos estatísticos (média e variância) se mantêm constantes (Morettin & Toloi, 2004). Percebe-se que para a modelagem de séries temporais deve-se utilizar uma série estacionária, de modo que no período de estimação seus parâmetros sejam representativos de toda a série que será estimada.

Os testes utilizados para verificar se as variáveis seguem um processo estocástico estacionário são os testes de raiz unitária de Dickley-Fuller Aumentado – ADF (1979), e o teste Kwiatkowski, Phillips, Schmidt e Shin - KPSS (1992). A utilização conjunta destes testes é que um corrobora o resultado do outro, em relação às raízes unitárias que são investigadas (Bueno, 2008).

Caso a série seja não-estacionária, as transformações são os procedimentos mais comuns para tornar a série estacionária. Em geral, a primeira diferença estacionariza a média e a segunda, a variância (Souza, Souza & Menezes,2013). Um cuidado que se deve ter neste sentido é no momento que a série já está estacionária com a primeira diferença, não havendo necessidade de se realizar diferenças posteriores, pois o excesso de diferenças pode incluir erros nas séries, levando a problemas posteriores no momento da modelagem desta série.

As componentes de uma série temporal são: a tendência, onde o seu comportamento ascendente ou descendente ocorre na série; ciclos, são suaves oscilações (subidas e quedas) que se repetem de forma irregular em um longo período de tempo; sazonalidade são as oscilações (subidas e quedas) regulares ocorridas durante  períodos do ano e, por ultimo, o erro é a diferença entre o valor previsto e o valor observado, é também chamado de resíduo, sendo uma importante medida para verificar a estimação do modelo ajustado.

A escolha pelo melhor modelo se dará pelos resíduos produzidos por ele, onde o modelo escolhido se dá no sentido que quanto menor o erro, mais adequado é o modelo. O ideal para o erro é o que a literatura chama de ruído branco, onde sua média é zero, sua variância é constante e são não autocorrelacionados ()).

As componentes de uma série temporal descrita acima podem ser representadas por uma classe geral denominada Modelos Autorregressivos Integrados e de Médias Móveis (ARIMA), Box & Jenkins (1970), os quais possibilitam tratar a autocorrelação das séries de dados, modelando a média condicional quando a variância dos erros é constante (Souza et al., 2013).

Os modelos Box & Jenkins, genericamente conhecidos por ARIMA (Auto Regressive Integrated Moving Averages), em português, por Autoregressivos Integrados de Médias Móveis, consistem no ajuste desses modelos a um conjunto de dados, onde a escolha da estrutura do modelo é baseada nos próprios dados (Morettin & Toloi, 2004). A série temporal pode ser modelada pelos filtros AR, MA, ARMA ou ainda ARIMA (Werner & Ribeiro, 2003). Podem ser representados pelas equações 1 a 4.

AR                                                                        (1)

MA                                                                      (2)

ARMA                       (3)

ARIMA          (4)

Onde:     Parâmetro AR;

                        → Parâmetro MA;

                        → Média do processo;

                        → número de diferenças para tornar a série estacionária;

                        → a série original;

                        → resíduos.

Os estágios da construção do modelo são a identificação do modelo provisório a ser ajustado, baseada nas funções de autocorrelações e autocorrelações parciais, na estimação de seus parâmetros por meio do Método de Mínimos Quadrados Ordinários e a validação do modelo por meio da inspeção dos resíduos. No caso de escolha de um modelo não adequado à série, este ciclo é repetido.

A definição pelo melhor modelo é baseada pelos critérios penalizadores: Bayesian Information Criterion – BIC e Akaike Information Criterion – AIC, conforme equações 5 e 6.

BIC = ln + n                                                                                          (5)

AIC = ln+ n ,                                                                                           (6)

Onde:     → é a variância do erro;

              T → é o número de observações utilizadas;

              N → é o número de parâmetros estimados.

 A decisão é realizada levando em conta a minimização dos critérios penalizadores, ou seja, o melhor modelo será o que apresentar os menores valores de AIC e BIC.

3. Metodologia

Para realização da modelagem foi utilizado um banco de dados retirado do site Agrolink, e este corresponde à produção mundial e anual de arroz em casca em mil toneladas, referente aos anos de 1961 a 2012, com coleta anual, formando uma série histórica mundial da produção de arroz com 52 observações.

A metodologia utilizada para a modelagem da série temporal será a de Box & Jenkins, utilizando como arcabouço os filtros do modelo ARIMA (Modelos Autoregressivos Integrados de Médias Móveis), de modo a tratar a autocorrelação presente nos dados, assim como as possíveis componentes de tendência e sazonalidade.

As etapas a serem cumpridas serão:

Análise da estabilidade da série, de modo a verificar se há a necessidade de se adotar procedimentos de diferenciação para estacionarizá-la, por meio dos testes ADF e KPSS;

Traçar as funções de autocorrelação e autocorrelação parcial, de modo a identificar os tipos de filtros a serem utilizados AR, MA, ARMA, ARIMA, e suas respectivas ordens de defasagens, assim como o número de diferenciações necessárias para tornar a série estacionária;

Identificado o tipo de filtro que será utilizado, realiza-se a estimação por meio do Método dos Mínimos Quadrados Ordinários;

Após essa etapa, investigam-se os resíduos, os critérios penalizadores AIC e BIC, de modo a identificar o melhor modelo entre os modelos concorrentes ajustados. O melhor modelo será utilizado para realizar previsões. O software utilizado para modelagem dos dados foi o EViews 8 S.V.

4. Aplicações e Discussão

Os dados coletados da produção mundial de arroz formam uma série histórica com 52 observações.

Percebe-se, pela inspeção gráfica da série original em estudo, na Figura 1, que ela apresenta uma tendência ascendente, com características aditivas, pois não há um crescimento proporcional de picos ou vales com o passar do tempo. Por exemplo, nos instantes entre 1970 e 1980, observam-se pequenos vales, e nos instantes de 1995 a 2005, outros pequenos vales, que se mantém proporcionais. Como o gráfico está plotado na mesma escala, não estão tão pronunciadas as evidências descritas. Caso contrário, se estes vales apresentassem um crescimento de um período para o outro, a série poderia ser multiplicativa. A série não apresenta evidência de sazonalidade, o que a corroborar a coleta de dados, que é anual.

Também observa-se na Figura 1 que, pelo fato da série apresentar tendência, ela é não-estacionária. Desta forma, foi necessário aplicar uma diferença, conforme pode-se observar na Figura 1, de modo a torná-la estacionária, possibilitando a estabilidade dos parâmetros estimados.

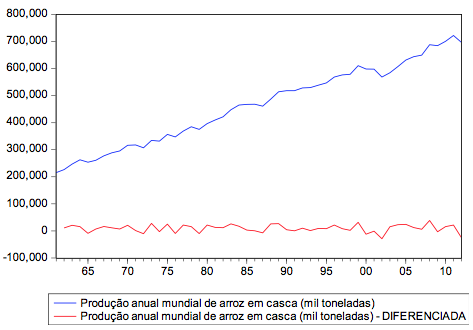
Figura 1 - Série original da Produção mundial de arroz e série com uma diferença

Para escolher uma classe de modelo adequado para representar o ARIMA (p, d, q) proposto por Box & Jenkins, (1970), traçou-se a função de autocorrelação e autocorrelação parcial, conforme Figura 2.

Figura 2 - FAC e FACP da série original

O melhor modelo ajustado foi um autoregressivo de ordem 1, com parâmetro significativo no lag 2, estimado pelo Método dos Mínimos Quadrados Ordinários, com uma diferença. A escolha deste modelo baseou-se nos critérios penalizadores AIC e BIC, apresentados na Tabela 2. Portanto, o melhor modelo para representar a Série da Produção Mundial de Arroz é o modelo AR(1).

Observa-se, pela Figura 2, que há um decaimento lento da função de autocorrelação, corroborando os resultados apresentados pelos testes ADF e KPSS, apresentados na Tabela 1, desta forma, a série precisa ser diferenciada para se estimar o modelo, que sugere ser um autoregressivo.

Tabela 1 - Resultados apresentados pelos testes ADF e KPSS

Notas: a Valores críticos de MacKinnon (1996):  -3.493.129 (1%); -2.888.932 (5%) e -2.581.453 (10%)
 b Valores críticos de Kwiatkowski-Phillips-Schmidt-Shin(1992, Table 1): 0.739 (1%); 0.463 (5%) e 0.347 (10%). 

Na Tabela 2, apresenta-se um modelo AR(1) em que o lag significativo foi o segundo, portanto representado por AR(2), embora a sua função de autocorrelação parcial indique que o primeiro lag seria o significativo. Entre os modelos concorrentes, este foi o que além de apresentar resíduos com características de ruído branco, apresentou as melhores características para os critérios AIC e BIC.

Tabela 2 - Estimação do modelo ARIMA (1,1,0)

Apresentam-se, na Figura 3, o exame dos resíduos por meio das funções de autocorrelação e de autocorrelação parcial dos resíduos oriundos do modelo AR(2), os resíduos apresentam-se não autocorrelacionados, e desta forma, os mesmos não apresentam informações adicionais ao modelo.

Figura 3 - FAC e FACP dos resíduos oriundos do modelo AR(2)

Observa-se na figura 4, que a série ajustada converge para a série original, isto é evidenciado pela série de resíduos que apresenta uma média zero, uma variância dentro do intervalo considerado de -20,000 como limite inferior até o limite superior de 20,000, mostrando assim, que esta variância é homocedástica.

Figura 4 - Série original da Produção mundial de arroz, série com uma diferença e série dos resíduos

Observado que todas as estatísticas de validação do modelo foram adequadas, realiza-se previsões in sample, de modo a verificar o comportamento futuro, conforme Figura 5.

Figura 5 - Previsão anual mundial de arroz

Desta forma, observa-se que o modelo estimado está apto para se realizar previsões, pois ele apresenta todas as condições impostas de um modelo adequado, observa-se também que todos os valores previstos apresentam-se dentro de um intervalo de confiança de 2 desvios-padrões. Desta forma, os tomadores decisões, cooperativas, redes de supermercados, podem tomar suas decisões em bases científicas.

5. Conclusões

O processo gerador da série é um processo autoregressivo de ordem 1, com parâmetro significativo no lag 2, que nos remete à produção mundial de arroz, e apresenta uma mudança significativa para mais a cada dois anos.

Com base no modelo ajustado, foi possível realizar a previsão in sample, o que evidencia esta tendência crescente ao longo dos anos. Não foram evidenciadas sazonalidades na série, possivelmente pelo fato da coleta de dados ser anual.

Neste estudo, verificou-se o comportamento da média condicional, representado por um modelo ARIMA. No entanto, seria interessante investigar o comportamento da variância condicional a média do processo, com a utilização dos modelos autoregressivos condicionais a heteroscedasticidade – ARCH.

Referências

Agrolink (acesso em setembro / 2015). Disponível em: http://www.agrolink.com.br/.

Bueno, Rodrigo de Losso da Silveira (2008). Econometria de séries temporais. São Paulo: Cengage Learning.

Conab. Companhia Nacional de Abastecimento (2011). Acompanhamento de Safra Brasileira: grãos. Quarto levantamento, janeiro 2011. Brasília: Conab. Disponível em: http://www.conab.gov.br/.

Menezes, Marcelo. (acesso em: agosto / 2015). INE 7001. Análise de Séries Temporais. Disponível em: http://www.inf.ufsc.br/~marcelo/Cap4.pdf.

Morettin, Pedro Alberto; Toloi, Clélia Maria de Castro (2004). Análise de Séries Temporais. São Paulo: Edgard Blücher.

Russo, Suzana Leitão; Ilgner, Norberto Otmar; Basso, Fernanda de Melo. (acesso em: setembro / 2015). Construção de modelos e previsão para explicação da entrada turística no Porto Mauá / Alba Posse. Disponível em: http://www.urisan.tche.br/~gep/2003/constmodelos.pdf.

Souza, Francisca Mendonça; Souza, Adriano Mendonça de; Menezes, Rui (2013). "Análise Empírica do Número de Consumidores e do Consumo de Energia Elétrica no Rio Grande do Sul por meio de Modelos Matemáticos". Revista Espacios, vol. 34, vol. 1. Disponível em: http://www.revistaespacios.com/a13v34n01/13340102.html.

Werner, Liane; Ribeiro, José Luis Duarte (2003). "Previsão de demanda: uma aplicação dos modelos Box-Jenkins na área de assistência técnica de computadores pessoais." Gestão & Produção. Vol. 10, n. 1.

Vieira, Adriana Carvalho Pinto; Brunch, Kelly Lissandra; Watanable, Melissa; Yamaguchi, Cristina Keiko; Neto, Roseli Jenoveva; Bolson, Edison Antonio (2012).  "A influência das inovações no campo: as cultivares produzidas na região Sul Catarinense no Brasil". Revista Espacios, vol. 33, n. 10. Disponível em: http://www.revistaespacios.com/a12v33n10/12331001.html.

1. Email: leticiamarasca@yahoo.com.br