HOME | ÍNDICE POR TÍTULO | NORMAS PUBLICACIÓN

Espacios. Vol. 37 (Nº 06) Año 2016. Pág. 29

Análise de séries temporais para previsão da evolução do número de automóveis no Município de Joinville

Time series analysis to forecasting the evolution of the cars in the city of Joinville

Amanda Caroline MARTIN 1; Elisa HENNING 2; Olga Maria Formigoni Carvalho WALTER 3; Andrea Cristina KONRATH 4

Recibido: 21/10/15 • Aprobado: 22/11/2015

Contenido

1. Introdução

2. Previsão de demanda

3. Procedimentos metodológicos

4. Resultados e discussão

5. Conclusões e considerações finais

6. Referências bibliográficas

1. Introdução

A grande competitividade existente na atualidade leva as empresas a buscarem métodos para produzirem de maneira mais eficiente e eficaz. Neste contexto, produzir a quantidade certa e na hora adequada é fundamental para manter a sustentabilidade empresarial. De acordo com Slack, Chambers e Johnston (2009), prever a demanda é necessário para melhorar o planejamento para o futuro.

Em um cenário competitivo, aplicar corretamente metodologias pode diminuir a imprecisão das previsões (SOUZA; SAMOHYL; MIRANDA, 2008) e permitir que a empresa produza com maior assertividade.            As séries temporais, que são sucessões de valores de determinada variável ao longo do tempo e, necessariamente, são ordenadas cronologicamente. A aplicação de previsões realizadas a partir de análise de séries temporais é relevante para o planejamento econômico e de negócios, planejamento de produção e otimização de processos industriais (BOX; JENKINS; REINSEL, 1994). Portanto, realizar previsões reduzirá o grau de incerteza e auxiliará na tomada de decisões. Assim, contribuirá para que a empresa, por exemplo, produza a quantidade adequada no momento oportuno, oferecendo maior acurácia na produção e adaptando-a as variações de mercado.

O estudo de séries temporais para previsão de crescimento de automóveis vai além da possibilidade de indústrias automobilísticas e revenda de carros preverem seu mercado futuro. Utilizar métodos de previsão para esta série de dados pode auxiliar o poder público em sua tomada de decisões, especialmente relacionada à infraestrutura, planejamento de tráfego e definição de políticas públicas devido à expansão da frota.

Portanto, entender o padrão de crescimento da frota de automóveis e encontrar um método para prever essa evolução é importante em diversos aspectos. Justifica-se, então, a importância da realização deste trabalho, que pretende responder à problemática de compreender a taxa de crescimento de automóveis, bem como prever o aumento desta categoria. 

Assim, o objetivo deste trabalho é analisar o crescimento da frota de automóveis em Joinville - SC. Para alcançar este objetivo será identificado um modelo de previsão a partir de séries temporais, especificadamente modelos autorregressivos integrados de média móvel e modelos de suavização exponencial.

Este artigo foi estruturado em cinco seções. A próxima seção descreve os modelos de previsão através de séries temporais a serem utilizados neste artigo. A seção 3 refere-se à metodologia utilizada para a realização da pesquisa e procedimentos para coleta de dados. Na seção 4 estão os resultados, que são os modelos propostos e análise de erro, além da discussão destes. Por fim, na seção 5estão as conclusões e considerações finais.

2. Previsão de demanda

A previsão de demanda é um processo para estimar as condições futuras de vendas, mercado ou outros fatores que podem influenciar na estratégia de uma organização. Para Martins e Laugeni (2005), corresponde processo metodológico para determinação de dados futuros baseados em modelos estatísticos, matemáticos ou econométricos ou ainda em modelos subjetivos apoiados em uma metodologia de trabalho clara e previamente definida.         

No âmbito proposto neste artigo, de demanda por automóveis, a importância da previsão vai além da análise de mercado, que pode favorecer o setor automobilístico (produção e revenda). Acredita-se que prever o crescimento do número de automóveis beneficia o poder público, pois pode colaborar na elaboração de políticas, além de contribuir significativamente para o planejamento de tráfego viário. É importante destacar que a previsão não é por si só, uma decisão, é apenas um meio de informação que auxiliará na toma de decisões (MORETTIN; TOLOI, 2006).

Existem diversos métodos de previsão e suas utilizações estão sujeitas a disponibilidade de dados, tempo e recursos, assim como ao horizonte de previsão (MOREIRA, 2008). As duas classificações mais comuns para os métodos de previsão são qualitativas e quantitativas (SLACK; CHAMBERS; JOHNSTON, 2009). Os métodos qualitativos são baseados em experiências ou intuição de gerentes ou consumidores, ou seja, são modelos subjetivos (LEMOS, 2006). Já os métodos quantitativos utilizam modelos matemáticos para se obter as previsões.

Entre os métodos quantitativos destacam-se os modelos causais e os de séries temporais (TAKEDA, 2012). Os métodos causais avaliam as causas e efeitos entre as variáveis, já as séries temporais simplesmente utilizam de dados passados para prever o futuro, sem considerar as variáveis causais.

De acordo com Moreira (2008), apesar de existirem distintos métodos de previsão, algumas características são comuns a todos: o comportamento do passado interfere no comportamento do futuro, ou seja, as previsões consideram de alguma maneira experiências anteriores e os resultados não são perfeitos, pois quanto maior o horizonte de predição, maior será o erro associado.

2.1 Séries temporais

Segundo Downing e Clark (2006, p. 299), "As séries temporais (ou históricas) são conjuntos de medidas de uma mesma grandeza, relativas a vários períodos consecutivos".  Ou seja, a série temporal é uma sucessão de valores de uma determinada variável observada em intervalos regulares de tempo. A variável de controle é o tempo e as séries temporais são ordenadas cronologicamente (SILVA; SILVA, 1999)e variar a ordem pode modificar a informação contida na série. Podem ser coletados em intervalos regulares de tempo, e podem ser observações diárias, mensais, trimestrais, anuais, entre outros. Como exemplo para as séries temporais é possível citar o preço das ações, valores de exportações, Produto Interno Bruto (PIB), temperatura, vendas médias de determinado item, temperatura média, batimentos cardíacos, enfim, uma infinidade de séries históricas e ordenadas cronologicamente podem ser reconhecidas como séries temporais.

Box, Jenkins e Reinsel (1994) citam quatro principais aplicações para a previsão por intermédio de séries temporais: planejamento econômico e de negócios, planejamento de produção, inventário e controle de produção e, por fim, controle e otimização de processos industriais. Realizar previsões por meio de um método estatístico reduz o grau de imprecisão sobre os valores futuros, o que auxilia na tomada de decisões. De acordo com Tubino (2007), a demanda futura será uma projeção dos valores pretéritos e não sofre influência de outras variáveis. Pode-se dizer que uma das limitações da série temporal é ela considerar apenas as observações passadas para realizar as previsões, sem considerar as variações causais (SLACK; CHAMBERS; JOHNSTON, 2009).

De acordo com Gujarati e Porter (2011), existem cinco métodos mais comuns para previsão econômica por meio de séries temporais, mas o presente trabalho se concentrará apenas nos métodos de suavização exponencial e processo autoregressivo integrado de média móvel (ARIMA).

De acordo com Souza, Samohyl e Miranda (2008) e Hyndmann e Athanasopolus(2013)as séries temporais possuem três padrões básicos: tendência, sazonalidade e ciclo. A tendência ocorre quando se verifica que os dados crescem ou diminuem ao longo do tempo. Podem existir casos em que a tendência mude de direção, por exemplo, ir de uma tendência crescente para uma decrescente. Já as séries que permanecem constantes ao longo do tempo não possuem tendência.

A sazonalidade ocorre quando a série sofre influência de fatores sazonais, por exemplo, o semestre ou dia do ano, sendo o período sempre conhecido (DOWNING; CLARK, 2006).Diferentemente da sazonalidade, as variações cíclicas ocorrem em períodos não conhecidos. Segundo Silva e Silva (1999)as variações sazonais "são movimentos cíclicos que se completam em um ano" enquanto as variações cíclicas "são movimentos cíclicos que se completam em período superior a um ano".

Downing e Clark (2006) também consideram a existência de outra componente, a irregular, pelo fato de haver algum movimento que não é explicável por tendência ou ciclos. De acordo com Silva e Silva (1999) essas variações irregulares ocorrem por acaso e contribuem para aumento ou queda de valores da série, e a contribuição para o acontecimento pode ser, por exemplo, de sobretaxas alfandegárias ocasionais e até guerras.

A principal característica que deve possuir uma série temporal é ela ser estacionária, ou seja, além de ser estocástico, o processo deve estar em equilíbrio em relação a uma média e com variância constante (BOX; JENKINS; REINSEL, 1994). Segundo Gujarati e Porter (2006), uma série não estacionária permite o estudo do seu comportamento apenas no período considerado, ou seja, não é possível utilizar para outros períodos, tornando-se de pouco valor para realizar previsões. Dificilmente as séries temporais são estacionárias, por exemplo, as séries financeiras apresentam tendências e, então, deve-se agir sobre os dados para tornar estacionária (MORETTIN; TOLOI, 2006). A partir de diferenciações é possível tornar a série estacionária.

Para analisar as séries temporais e verificar como as observações futuras são influenciadas pelas do passado, se utilizam as funções de autocorrelação amostral (ACF) e autocorrelação amostral parcial (PACF). A ACF (ou correlograma) proporciona a estrutura de dependência linear da série, ou seja, como uma observação influência sobre as posteriores. Já a PACF (ou correlograma parcial) mostra o grau de associação linear direta entre observações separadas por k períodos. Segundo Ehlers (2009), através do correlograma é possível verificar as seguintes propriedades das séries temporais: aleatoriedade, sazonalidade, correlação e estacionariedade. Já a tendência pode ser observada por meio  do gráfico da série.

2.2 Processo autoregressivo integrado de média móvel

Para facilitar o entendimento de um processo autoregressivo integrado de média móvel (ARIMA), diversos autores optam por explicar separadamente cada componente. Assim, considerando-se uma série estacionária, existem algumas formas para modelá-la, como processo autoregressivo (AR), processo de média móvel (MA) e processo autoregressivo de médias móveis (ARMA). Os modelos ARIMA são utilizados para séries estacionárias, bem como os modelos SARIMA, que consideram uma componente sazonal (BOX; JENKINS; REINSEL, 1994;MORETTIN; TOLOI, 2006; EHLERS, 2009; GUJARATI; PORTER, 2011; HYNDMAN; ATHANASOPOULOS, 2013).

Para identificar facilmente os modelos, foram analisadas a função de autocorrelação amostral (ACF) e função de autocorrelação amostral parcial (PACF). Os métodos descritos a seguir para modelagem de séries temporais estacionárias, séries temporais não estacionárias e a metodologia Box-Jenkins foram extraídos dos estudos de Box, Jenkins e Reinsel (1994), Morettin e Toloi (2006),Ehlers (2009), Gujarati e Porter (2011)e Hyndman e Athanasopoulos (2013).

A Tabela 1 é útil para sintetizar as informações de identificação dos modelos por meio da função de autocorrelação (ACF) e  função de autocorrelação parcial(PACF).

Tabela 1 - Comparativo entre os modelos AR(p), MA(q) e ARMA(p,q)

Fonte: Gujarati e Porter (2011).

Considerando que a série é não estacionária, torna-se necessário diferenciá-la, assim é possível utilizar um modelo autorregressivo integrado de média móvel (ARIMA) para a série (GUJARATI; PORTER, 2011).

Os modelos ARIMA (p,d,q) diferem-se dos modelos ARMA(p,q) apenas pela diferenciação que ocorre d vezes, até tornar a série estacionária. Normalmente apenas uma ou duas diferenciações são necessárias para que a série se torne estacionária. Estabelecida uma série estacionária após d diferenciações, segue-se o procedimento de identificação de um modelo ARMA(p,q).  As séries sazonais apresentam uma parte regular e outra sazonal, sendo representada por ARIMA(p,d,q)x(P,D,Q)s, sendo s o período sazonal da série e podem ser chamados de modelo SARIMA.

A sazonalidade é também uma causa de não estacionariedade da série e, caso necessário, deve haver diferenciações para torná-la estacionária. Em um cenário que há sazonalidade, mas a série é não estacionária também por outros motivos, só será necessário diferenciá-la sazonalmente caso a diferenciação da parte regular não a tenha tornado estacionária na parte sazonal. A diferenciação da parte sazonal é representada por D e é similar à parte regular, no entanto, ocorre nos períodos sazonais. A maneira para identificar um modelo SARIMA é bastante similar a que ocorre em um modelo ARIMA: observam-se as funções de autocorrelação amostral e autocorrelação amostral parcial, no entanto, os períodos avaliados são múltiplos de s.

Para facilitar o processo de escolha do melhor modelo, pode-se proceder de acordo com a metodologia iterativa Box-Jenkis (Figura 1), constituída de quatro fases após conhecimento das classes gerais dos modelos, apresentados nos itens anteriores.

Figura 1 - Metodologia Box-Jenkins

Fonte: Adaptado de Box, Jenkins e Reinsel (1994).

Na primeira etapa da metodologia Box-Jenkins utilizam-se as funções de autocorrelação amostral e autocorrelação amostral parcial para identificação do modelo. Esta pode ser considerada a etapa crítica da metodologia, pois uma mesma série temporal pode ser identificada por distintos modelos.  Na estimação, após escolhido um modelo, estimam-se os seus coeficientes, normalmente através de métodos computacionais. A fase de diagnóstico verifica-se a adequação do modelo que corresponde à análise dos resíduos. O modelo mais adequado é aquele que possui o menor erro, resíduos normais e não correlacionados. Caso não seja encontrado um modelo adequado, volta-se à fase de identificação do modelo, visto que a metodologia Box-Jenkins é iterativa. A partir do modelo considerado adequado é possível realizar a previsão dos valores futuros. É recomendável reservar algumas observações para avaliar o erro também da previsão, ou seja, fora da amostra, que também pode auxiliar na escolha do modelo.

2.3 Suavização exponencial

Assim como os modelos autoregressivos integrados de média móvel, os métodos de previsão por suavização exponencial não consideram as variações causais. Segundo Morettin e Toloi (2006), este método visa identificar o padrão da série, através da suavização dos seus extremos, que representam a aleatoriedade. A suavização decompõe a série em tendência e sazonalidade e atribui pesos diferentes às observações, valorizando os dados mais atuais. (SOUZA; SAMOHYL; MIRANDA, 2008).

Existem quatro métodos mais comuns de suavização exponencial: médias móveis simples (MMS), suavização exponencial simples (SES), suavização exponencial de Holt (SEH) e suavização exponencial sazonal de Holt-Winters (HW). Estes quatro métodos serão descritos, conforme exposto por Souza, Samohyl e Miranda (2008), Morettin e Toloi (2006), Ehlers (2009) e Hyndman e Athanasopoulos (2013).

O método de médias móveis simples (MMS) é utilizado para as séries de dados sem padrão sazonal e tendência. Neste método supõe-se que todas as observações são de igual importância, portanto o peso atribuído a elas é o mesmo. As previsões futuras serão a média simples dos dados observados. Este é um método de simples aplicação e pode ser aplicado quando se tem um pequeno número de observações. No entanto, este método muitas vezes não é adequado, pois se acredita que as observações mais recentes são de maior importância para realizar previsões.

O método de suavização exponencial simples (SES) também é utilizado apenas em séries sem tendência ou sazonalidade. No entanto, diferentemente do MMS, no SES as observações possuem pesos distintos, atribuindo-se valores maiores às observações mais recentes, enquanto o peso atribuído às mais antigas decai exponencialmente. Quanto maior o peso atribuído, menor é a suavização. Portanto, menores pesos proporcionam previsões mais estáveis.

Os dois métodos anteriores não funcionam para séries que possuem tendência. O método de suavização exponencial de Holt (SEH) é bastante similar ao SES, a diferença é que este método suaviza não só o nível, mas também modela a tendência da série. Portanto, a realização de previsões se dá atribuindo pesos para as duas componentes. 

O método de suavização exponencial sazonal de Holt-Winters (HW) considera, além da tendência, a sazonalidade da série. Este método possui, então, três componentes: nível, crescimento e sazonalidade. O fator sazonal pode ser aditivo ou multiplicativo. No método aditivo, a sazonalidade é somada à tendência da série, já no método multiplicativo, a sazonalidade é multiplicada pela tendência.

Para classificar os métodos de suavização exponencial, deve-se considerar o comportamento da tendência e da sazonalidade da série. A tendência pode ser caracterizada em cinco tipos: nenhuma, aditiva, aditiva amortecida, multiplicativa e multiplicativa amortecida; já a sazonalidade é classificada em: nenhuma, aditiva e multiplicativa. Ao considerar essas variações, pode-se verificar a existência de 15 métodos, conforme Tabela 2.

Tabela 2 - Métodos de Suavização Exponencial

Fonte: Adaptado de Souza, Samohyl e Miranda (2008).

O método NN é o de suavização exponencial simples, o AN é o método de Holt, AA é Holt-Winters Aditivo e AM é Holt-Winters Multiplicativo. Para cada um dos métodos existem erros, aditivos ou multiplicativos. Um modelo MNN é a suavização simples com erro multiplicativo, indicado pelo M. Já um modelo ANN é a suavização simples com erro aditivo, indicado pelo A. Logo, pode-se considerar a Tabela 2 duas vezes, uma para o erro aditivo e outra pelo multiplicativo. No entanto, algumas das combinações não são válidas para selecionar o modelo, devido a dificuldade numérica. São eles: MMA, MMaA, ANM, AAM, AAaM, AMN, AMA, AMM, AMaN, AMaA e AMaM. Portanto, para erro aditivo, pode-se trabalhar com seis modelos e, para o erro multiplicativo, treze modelos.

2.4 Avaliação dos modelos

Realizam-se duas etapas para a avaliação dos modelos de previsão. A primeira consiste no diagnóstico do modelo e diz respeito à análise residual, que informará se o modelo proposto atende as condições estabelecidas e a segunda etapa é a análise dos erros de previsão. Realizado o diagnóstico e comprovada a adequação dos resíduos, efetua-se um estudo dos erros de previsão, para definição do modelo que melhor representa a série temporal.

A diferença entre uma observação é seu valor ajustado é chamado de resíduo (MONTGOMERY; RUNGER, 2003). Se o modelo proposto representa adequadamente os dados, então, os resíduos devem possuir as características de um ruído branco. Um ruído branco é um tipo especial de série estacionária, que possui média zero, variância constante e não é serialmente correlacionado (GUJARATI; PORTER, 2006). Se os resíduos não são um ruído branco, entende-se que há informação que deve ser incorporada ao modelo proposto. Segundo Ehlers (2009), deve-se incluir no modelo informações caso haja autocorrelação nas defasagens 1 ou 2 ou, então, nos períodos sazonais. O mesmo ocorre para a autocorrelação parcial. Caso a defasagem ocorra em outros pontos, não há evidências suficientes para rejeitar o modelo. 

Para análise da normalidade de resíduos pode-se utilizar, entre outros, o testes Shapiro Wilk. Já para verificação da correlação residual, pode-se realizar os testes Box-Pierce e Ljung-Box. Estes testes podem ser realizados de maneira automática por meio de softwares e, portanto, optou-se por suprimir as fórmulas.  De acordo com Morettin e Toloi (2006, p. 205) "o ciclo de identificação, estimação e verificação deve ser continuado, até que um modelo satisfatório seja encontrado".

Após o diagnóstico dos modelos realizado por meio da análise de resíduos e comprovada adequação, estima-se o erro de previsão dos modelos considerados adequados. O melhor modelo é aquele que apresentar o menor erro.

Os erros podem ser analisados dentro e fora da amostra. Os erros fora da amostra correspondem ao comparativo de previsão versus valores reais; já os erros dentro da amostra são obtidos a partir da estimação do modelo, sem comparação com valores reais.  Para que seja possível realizar a análise fora da amostra, algumas observações devem ser reservadas. No caso proposto, das 142 observações, 130 serão utilizadas para estimar o modelo e as outras 12 para verificar o erro gerado relacionado à previsão.

As previsões não são exatas e o erro associado é maior quanto maior for o horizonte de predição (MOREIRA, 2008). De acordo com Souza, Samohyl e Miranda(2008) existem distintas maneiras de se avaliar a qualidade das previsões, sendo os índices de erro mais conhecidos descritos a seguir.

Espera-se que os valores de  variem sempre entre zero e um para indicar modelos de previsão adequados, sendo melhores as previsões que se aproximam de zero. Erro superior a um indica que o modelo proposto possui erro superior ao passeio aleatório (EHLERS, 2009).

3. Procedimentos metodológicos

Do ponto de vista da natureza, pode-se classificar a pesquisa como aplicada, pois visa obter conhecimento que poderá ser utilizado na prática (GIL, 2010). É também classificada como  quantitativa, devido à característica da análise dos dados. Segundo os procedimentos técnicos utilizados, a pesquisa pode ser classificada como ex-post facto e estatística. Caracteriza-se como ex-post facto pois os dados foram obtidos "a partir do fato passado" (GIL, 2010) e como estatística porque representa e explica, por meio de gráficos e quadros, as observações quantitativas (FACHIN, 2001).

Os dados foram obtidos no site de internet do Detran-SC (DETRAN, 2015), que possui uma base de constantemente atualizada com os todas as categorias de veículos emplacados em cada município do estado. As informações utilizadas neste trabalho são observações mensais desde janeiro de 2003 a fevereiro de 2015.

A análise dos dados foi realizada com o auxílio do software R (R CORE TEAM, 2015). Para a análise de séries temporais, fez-se uso da função "forecast"(HYNDMAN; KHANDAKAR, 2008), com o qual é possível realizar as previsões de demanda pelos métodos ARIMA e Suavização Exponencial. Este trabalho possui dois modelos diferentes para a previsão de demanda: modelo ARIMA, proposto a partir da interpretação de dados e automático com auxílio do pacote forecast, modelo de suavização exponencial, proposto e automático. Foi realizada a análise dos resíduos para verificar a adequação dos modelos e também avaliados os erros de previsão dentro e fora da amostra (ME, MAE, RMSE e MAPE) além da estatística U de Theil. Para a verificação dos erros de previsão, as 12 últimas observações, abril de 2014 até março de 2015, foram reservadas para avaliar a acurácia das previsões fora da amostra.

4. Resultados e discussão

A série temporal considerada para o estudo corresponde ao conjunto de observações mensais desde janeiro de 2003 a março de 2014 dos automóveis, caminhonetes, camionetas e utilitários do município de Joinville – SC. Estas quatro categorias representam aproximadamente 73,4% do total de automóveis da cidade e, para facilitar a sua referência no decorrer da análise da série, serão denominadas apenas por automóveis. A Figura 2 apresenta o gráfico das funções de autocorrelação amostral e autocorrelação amostral parcial, bem como o comportamento dos dados ao longo dos meses.

Figura 2 - Apresentação da Série Temporal

Fonte: Primária (2015).

A série é não estacionária, visto que uma tendência crescente é facilmente identificável na Figura 2. Pode-se, também, decompor a série para verificar os componentes de sazonalidade e efeito aleatório, como mostra a Figura 3.

Figura 3 - Decomposição da série temporal

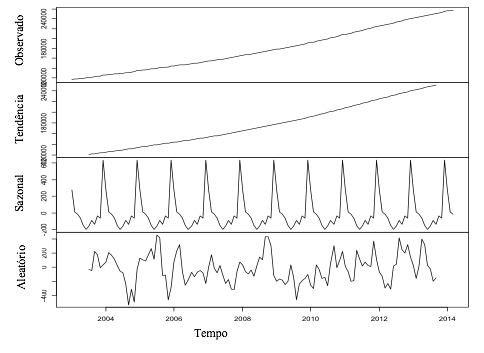
Fonte: Primária (2015).

Para esta série de dados, nota-se que a componente tendência é bastante similar aos dados observados e identifica-se que existe sazonalidade, pois esta componente apresenta padrão repetitivo, observado no terceiro gráfico da Figura 3.

Para a estimação do melhor modelo para realização de previsões, foram propostos alguns modelos entre os autorregressivos integrados de média móvel e os de suavização exponencial.  Para melhor avaliar a estacionareidade foram realizados três testes, a saber: Teste de Kwiatkowski, Phillips, Schmidt e Shin (KPSS), Teste Aumentado de Dickey Fuller  (ADF) e Teste de Phillips-Perron (PP). O objetivo foi verificar o número necessário de diferenciações na parte regular, conforme Tabela 3.

Tabela 3 – Diferenciações regulares

Fonte: Primária (2015).

Um teste apontou a necessidade de apenas uma diferenciação, os demais mostraram ser necessário diferenciar duas vezes. Foi realizada, então, a primeira e segunda diferenciação, apresentadas no primeiro e segundo gráfico da Figura 4, respectivamente.

Figura 4 - Diferenciações da Série Não Estacionária

Fonte: Primária(2015).

Realizaram-se os testes Osborn, Chui, Smith e Birchenhall (OCSB) e Teste Canova e Hansen (CH)para verificar a necessidade de diferenciação sazonal após a realização da primeira e da segunda diferenciação regular. Em ambos os casos houve indicação de que não seria necessário realizar a diferenciação.

Parte-se, então, para a proposição de modelos. Pode-se supor modelos a partir da análise dos gráficos ou gerar modelos automáticos através de software.

O software R, por meio do pacote forecast (HYNDMAN; KHANDAKAR, 2008)possui funções para propor automaticamente modelos autorregressivos. O modelo assim gerado foi um ARIMA Sazonal (SARIMA) , denominado Modelo I. Os resíduos apresentam característica de ruído branco, são normais e não correlacionados. No entanto, o erro U-Theil fora da amostra apresentou um valor superior a um e, portanto, essa informação foi suficiente para descartar o modelo para realizar previsões.

            Além deste modelo, outros modelos foram propostos, definidos a partir das análises visuais dos gráficos ACF e PACF. Ao todo, cinco modelos foram selecionados por apresentarem os resíduos com distribuição normal e não correlacionados. Os respectivos modelos são apresentados na Tabela 4.

Tabela 4 – Comparativo entre os modelos ARIMA

*NA: Não aplicável
Fonte: Primária (2015).

A partir da Tabela 4 pode-se observar que o modelo automático (Modelo II) é o que apresentou os maiores erros. O melhor modelo, dentre os apresentados na Tabela 4 é o Modelo IV, pois possui erros menores. Além disso, é o mais parcimonioso, pois tem poucos parâmetros ou seja, valores pequenos de p,d,q e P,D,Q.

4.1 Modelos de Suavização exponencial

O pacote forecast também permite gerar automaticamente um modelo de suavização exponencial. O modelo que o software retorna é um ETS(x,x,x), onde ETS significa Error, Trend, Seasonal, ou seja, erro, tendência e sazonalidade.  O erro pode ser aditivo (A) ou multiplicativo (M), a tendência pode não ocorrer (N), ser aditiva (A), aditiva amortecida (Aa), multiplicativa (M) ou multiplicativa aditiva (M), já a sazonalidade pode não ocorrer (N), ser aditiva (A) ou multiplicativa (M). Nos casos onde não há tendência ou sazonalidade, os métodos de suavização exponencial serão diferentes do HW.

A partir da apresentação da série temporal e dos gráficos da série decomposta, sabe-se que a série possui tendência e sazonalidade. Portanto, o método escolhido é o de suavização exponencial sazonal de Holt-Winters.  

Inicialmente, testou-se o modelo automático, que retornou o Modelo A, um ETS (A,A,A), ou seja, erro, tendência e sazonalidade aditivos. O teste de normalidade e correlação dos resíduos apontaram que o modelo é adequado (Tabela 4). Optou-se por gerar um modelo de erro multiplicativo, com tendência e sazonalidade aditivas e comparar com o proposto.  O modelo ETS(M,A,A), denominado Modelo B, possui resíduos não correlacionados e os correlogramas não apresentam defasagens significativas. As medidas dos erros de previsão estão na Tabela 5.

Tabela 5 – Comparativo entre os modelos ETS

*NA: Não aplicável
Fonte: Primária (2015)

A partir da comparação entre os Modelos A e B, observa-se que o proposto apresenta erros um pouco menores que os do modelo automático. Todavia os valores da estatística U-Theil próximos a um sinalizam para um modelo pouco acurado para previsões.

Escolheu-se, então, que dentre os modelos autoregressivos e de média móvel, o Modelo IV foi o que melhor representou a série temporal de crescimento de automóveis em Joinville e, portanto, o mais indicado para realizar previsões. Seus valores observados estão sumarizados na Tabela 6, que contém também os valores reais da série, além dos erros individuais.

Tabela 6–Modelo IV

Fonte: Primária (2015).

A Figura 5 apresenta o gráfico com valores observados (linha contínua em azul) e previstos (linha contínua em vermelho) a partir do Modelo IV, com as respectivas faixas, em cor cinza, dos intervalos de confiança, para todo o período analisado.  No detalhe estão representadas as previsões pontuais e respectivos intervalos para o período de abril de 2014 até janeiro de 2015. Pode-se visualizar que o modelo representa bem a série avaliada.

Figura 5 - Gráfico de previsão para o Modelo IV

Fonte: Primária (2015).

5. Conclusões e considerações finais

Os métodos de previsão são fundamentais para auxiliar na tomada de decisão, visto que por meio deles é possível encontrar modelos que fornecerão informações sobre vendas futuras, por exemplo, ainda que com certo grau de imprecisão. A análise dos erros é, portanto, fundamental na escolha do melhor modelo.

Para a série temporal de crescimento do número de automóveis em Joinville-SC, a previsão é importante especialmente ao governo, visto que o entendimento do crescimento de automóveis permite estudos e implantação de políticas públicas e alterações de tráfego com maior precisão. Além disso, também pode servir ao setor automobilístico, de produção e revenda, ao entender o crescimento do mercado.

Foram ajustados alguns modelos e ao final, concluiu-se que o modelo que melhor representou a serie analisada foi o ARIMAEntende-se que este estudo pode ser replicado para outros municípios ou estados, assim como para outros modais de transporte. Outra sugestão é realizar o estudo considerando as variáveis causais, ou seja, propor modelos econométricos a fim de realizar previsões e verificar se o erro é menor que os modelos autorregressivos integrados de médias móveis.

O estudo de previsão de crescimento de automóveis e outros modais é, portanto, importante não somente no meio acadêmico ou empresarial, mas especialmente no quesito mobilidade, pois o conhecimento da evolução de demanda por diferentes modais possibilita aos órgãos públicos o dimensionamento urbano, desenvolvimento de tráfego, entre outros.

6. Referências bibliográficas

BOX, G. E. P; JENKINS, G. M.; REINSEL, G. C. Time Series Analysis: Forecasting and Control. 3 ed. New Jersey: Prentice Hall, 1994.

DETRAN/SC. Departamento Estadual de Trânsito. Frota de veículos por município (mensal). Disponível em: <http://consultas.detrannet.sc.gov.br/Estatistica/Veiculos/>. Acesso em: 25 mar. 2015.

DOWNING, D; CLARK, J. Estatística Aplicada.2 ed. São Paulo: Saraiva, 2006.

EHLERS,R.S.Análise de Séries Temporais. 5 ed. 2009.Disponível em: <http://www.icmc.usp.br/~ehlers/stemp/stemp.pdf>. Acesso em 15:fev 2015.

FACHIN, O. Fundamentos de Metodologia.3ed. São Paulo: Saraiva, 2001.

GIL, A.C. Como Elaborar Projetos de Pesquisa. 5ed.São Paulo: Atlas, 2010.

GUJARATI, D. N.; PORTER, D.C. Econometria Básica. 5 ed. Porto Alegre: AMGH, 2011.

HYNDMAN, R. J.; ATHANASOPOLUS, G. Forecasting: principles and practice. 2013. Disponível em: <https://www.otexts.org/fpp/>. Acesso em: 15 fev. 2015.

HYNDMAN, R. J.; KHANDAKAR, Y. Automatic time series forecasting: The forecast package for R. Journal of Statistical Software, v.27, n.3, p.1-22, 2008.

LEMOS, O. L. Metodologia para Seleção de Métodos de Previsão de Demanda, 2006. 183 f. Dissertação (Mestrado em Engenharia de Produção). Universidade Federal do Rio Grande do Sul, Porto Alegre.

MARTINS, P. G.; LAUGENI, F. P. Administração da Produção. 2.ed.  São Paulo: Saraiva, 2005.

MONTGOMERY, D. C.; RUNGER, G. C. Estatística Aplicada e Probabilidade para Engenheiros. 2 ed.  Rio de Janeiro: LTC, 2003.

MOREIRA, D.A., Administração da Produção e Operações. 2.ed.São Paulo: Cengage, Learning, 2008.

MORETTIN, P. A.; TOLOI, C. M. C. Análise de séries temporais. 2 ed. São Paulo: Edgard Blücher, 2006.

R CORE TEAM.R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria, 2015.Disponívelem: <http://www.R-project.org>. Acesso em: mai.2015.

SLACK, N.; CHAMBERS, S.;JOHNSTON, R. Administração da Produção.3 ed. São Paulo: Atlas, 2009.

SILVA, E. M;SILVA, E. M. Matemática e Estatística Aplicada. São Paulo: Atlas, 1999.

SOUZA, G. P.; SAMOHYL, R. W.; MIRANDA, R. G. Métodos Simplificados de Previsão Empresarial. Rio de Janeiro: Ciência Moderna, 2008.

TAKEDA, T. Proposta de Aplicação de Método Quantitativo de Previsão de Vendas em um Indústria Metal-Mecânica. 2012. 71 f. Trabalho de Graduação (Bacharelado em Engenharia de Produção e Sistemas). Universidade do Estado de Santa Catarina, Joinville.

TUBINO, D. F. Planejamento e Controle da Produção. São Paulo: Atlas, 2007.

1. Universidade do Estado de Santa Catarina - Centro de Ciências Tecnológicas. E-mail: amandacarolinimartin@gmail.com
2. Universidade do Estado de Santa Catarina - Centro de Ciências Tecnológicas. E-mail:elisa.henning@udesc.br

3. Universidade do Estado de Santa Catarina - Centro de Ciências Tecnológicas. E-mail: olgaformigoni@gmail.com
4. Universidade Federal de Santa Catarina – Departamento de Informática e Estatística. E-mail: andrea.ck@ufsc.br