HOME | ÍNDICE POR TÍTULO | NORMAS PUBLICACIÓN

Espacios. Vol. 37 (Nº 04) Año 2016. Pág. 5

Curva de Kuznets Ambiental: Análise das variáveis renda e dióxido de carbono para Europa e África

Curve de Ambient Kuznets: Analysis of the variable income and carbon dioxide for Europe and Africa

Fernando Ártico BIGARANI 1; Irene Domenes ZAPPAROLI 2; Umberto Antonio SESSO FILHO 3; Paulo Rogério Alves BRENE 4; Marcia Regina Gabardo da CAMARA 5

Recibido: 23/09/15 • Aprobado: 13/10/2015

Contenido

1. Introdução

2. A Curva de Kuznets Ambiental e o Protocolo de Kyoto
3.  Procedimentos metodológicos
4 . Relação Mundial entre Renda e Emissão de Dióxido de Carbono
5. Considerações Finais
Referências

Anexo

1. Introdução

O progresso econômico é responsável pela geração de renda, emprego e, principalmente, pelo aumento da riqueza da sociedade como um todo. Entretanto, o crescimento do Produto Interno Bruto (PIB mundial) gera na exploração de algumas atividades impacto ambiental. O aumento da emissão de gás carbônico é uma das externalidades negativas do crescimento da economia, por ser este o principal gás responsável pelo aquecimento global.

A camada gasosa que envolve a Terra é chamada de Atmosfera, tem como principais atribuições à filtração da radiação, a regulação do clima, do ciclo das chuvas, dos ventos, do efeito estufa, o fornecimento de oxigênio para a manutenção da vida, e a proteção contra a queda de meteoros. Algumas destas funções estão sofrendo alterações, devido ao aumento das emissões de certos gases, como o Dióxido de Carbono (CO2), Metano (CH4), Óxido nitroso (N2O), Clorofluorcarbonetos (CFCs), Hidrofluorcarbonetos (HFCs) e Hexafluoreto de enxofre (SF6). O Dióxido de Carbono é o gás mais emitido pela atividade humana, representando aproximadamente mais de dois terços dos gases lançados à atmosfera, portanto, o principal responsável pelo aquecimento global.

Nesse sentido o objetivo do artigo é verificar o formato da Curva de Kuznetz Ambiental na relação entre emissão de dióxido de carbono e o crescimento da renda. Procura-se verificar os efeitos do protocolo de Kyoto na emissão de poluentes e o formato da Curva de Kuznets Ambiental. Os objetivos específicos compreendem: verificar a existência de relação espacial entre emissão de CO2 per capita e PIB per capita por meio da Estatística Índice de Moran; identificar clusters e verificar o formato da curva de Kuznets por meio da análise dos resultados obtidos nas regressões espaciais entre os anos de 1994 e 2009, para os países da África e Europa.

Além desta introdução, esta pesquisa está organizada em outras quatro seções. A primeira seção apresenta uma revisão literária sobre curva de Kuznets Ambiental (CKA) e do protocolo de Kyoto. Na segunda tem-se a metodologia e o procedimento de preparação dos dados. A terceira seção traz os mapas obtidos por meio do programa Geoda para a análise univariada e bivariada de CO2 per capita e PIB per capita e suas respectivas considerações. Têm ainda nessa seção as análises do modelo clássico de regressão e do erro e suas respectivas conclusões com relação ao formato da CKA. Sendo, a última parte, dedicada a apresentação das conclusões e sugestão de novas pesquisas.

2. A Curva de Kuznets Ambiental e o Protocolo de Kyoto

A curva de Kuznets Ambiental e o Protocolo de Kyoto são os marcos ordenadores da revisão sobre a relação entre dióxido de carbono e renda per capita. No ano de 1997, na Conferência das Partes 3 (COP-3) o documento definido como protocolo de Kyoto, definiu metas de redução nas emissões de gases do efeito estufa (GEE). Os países foram divididos em dois grupos: os classificados no Anexo I e os Não-Anexo I (aqueles não inclusos no primeiro anexo). Nesse documento a redução da emissão de GEE ficou estabelecida em, no mínimo 5,2%, abaixo dos níveis de 1990, com base nos inventários nacionais apresentados, até 2012, para países do Anexo I. (Brasil, MMA, 2014)

Para entrar em vigor era necessário que 55 países ratificassem o protocolo e que estivessem incluídos os países desenvolvidos que são responsáveis por no mínimo 55% das emissões de CO2 em 1990. Os EUA assinaram o protocolo em novembro de 1998. (Thomas; Callan, 2012) Em março de 2001 os Estados Unidos se retiram do protocolo de Kyoto, desencadeando uma preocupação em relação ao futuro do protocolo, já que este é responsável por aproximadamente 25% das emissões mundiais de GEE. Entretanto, no mesmo ano 178 países chegaram a um acordo sobre as mudanças climáticas, sendo a ratificação obtida em 2004 depois da assinatura da Rússia e com a participação de 141 países. O Protocolo na versão final define que 38 países desenvolvidos reduzam suas emissões de GEE para 5,2% abaixo de seus níveis de 1990 até 2012. (Thomas; Callan, 2012)

Os compromissos assumidos no protocolo de Kyoto estabelecem metas para limitar ou reduzir as emissões, que foram expressas em níveis de emissões permitidas ou quantidades atribuídas e estas foram divididas em unidades de quantidades atribuídas (Assigned Amount Units – AAUs). Outro marco importante na discussão é a publicação do trabalho de Simon Kuznets, publicado inicialmente em 1955. Ao estudar a economia dos Estados Unidos, Grã-Bretanha e Alemanha, o atuor percebeu uma relação entre crescimento econômico e distribuição da renda pessoal em formato de U-invertido. Os diferenciais de rendimentos dos trabalhadores entre os setores da economia, na transição de uma economia agrícola para uma economia industrial, é a sua explicação para esse comportamento.  (Arraes et al., 2006)

No discurso que ficou conhecido como Economic Growth and Income Inequality, Kuznets sugeriu que no início o aumento da renda per capita leva a aumentos na desigualdade de renda, entretanto, tal relação se mantém apenas até certo ponto. Com o crescimento econômico continuado a relação entre as variáveis se moveria na direção de uma maior igualdade, ou seja, a partir de certo nível os aumentos da renda levariam a uma maior igualdade na distribuição da mesma. (Yandle et al., 2002). Tal relação que ficou conhecida como a curva de Kuznets

Lomborg (2002, p.42) argumenta que nos estágios iniciais de crescimento, a degradação ambiental ocorre como um efeito colateral ruim que, contudo, não será mais aceito a partir de certo nível de bem-estar econômico. Por um período de aproximadamente 300 anos, o ocidente viu sua renda aumentar e poluição também. Mas que no período recente, a intervenção ambiental tornou-se necessária para prevenir níveis de poluição indesejados.

O conceito de que a preservação ambiental depende do crescimento econômico, não leva em consideração, que os efeitos deste quanto ao meio ambiente não podem ser ignorados, e que capacidade do planeta não pode suportá-lo indefinidamente. Se a degradação for irreversível, a atividade econômica pode estar em risco (Arrow et al., 1995). Pode-se, entretanto, tratar do crescimento econômico e da preservação ambiental de forma conjunta, possibilitando a melhoria de ambos simultaneamente. O relatório "Nosso Futuro Comum" reconheceu uma falsa dicotomia entre meio ambiente e crescimento econômico, ambos não constituem desafios separados. O desenvolvimento não se mantém se a base de recursos ambientais se deteriora; o meio ambiente não pode ser protegido se o crescimento econômico não leva em conta as consequências da destruição ambiental (CMMAD, 1988).

Alguns autores, levando em conta o cenário econômico de seu período (década de 90) e a teoria da curva de Kuznets, criaram o conceito da curva de Kuznets ambiental (CKA). A CKA descreve a trajetória da poluição de um país como resultado de seu desenvolvimento em um determinado período de tempo. Ela prevê que a degradação ambiental se eleva à medida que o crescimento econômico aumenta; isto nos estágios iniciais do desenvolvimento, e, conforme o tempo, se alcançará um certo nível de renda que fará tal degradação diminuir. (Almeida; Carvalho, 2010)

Supondo um país que possui níveis de pobreza altos, quando o crescimento deste começa a ocorrer, a produção se eleva e sua poluição também crescerá. Por outro lado, a sua pobreza pode limitar os esforços de despoluição,  fazendo-o utilizar pouca ou nenhuma técnica de controle de poluição sobre a sua produção. À medida que a renda desse país emerge para níveis mais altos e sua produção se torna mais competitiva, a prioridade deste país muda para a proteção da qualidade ambiental, ou seja, a melhoria ambiental está relacionada com o crescimento econômico. (Almeida; Carvalho, 2010) Assim a curva de Kuznets no formato de U invertido tornou-se um meio para descrever a relação entre os níveis medidos de qualidade ambiental, tais como a que foi utilizada neste trabalho, emissões de dióxido de carbono per capita e renda per capita, ao longo do tempo.(Gráfico 1)

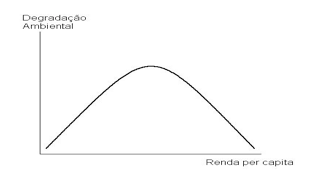
Fonte: LOMBORG, (2002, p.210)
Gráfico 1 - Curva de Kuznets Ambiental (CKA)

Os níveis mais baixos de renda per capita normalmente são encontrados nas economias pré-industriais e agrárias, onde a maioria da atividade econômica é a agricultura de subsistência, é de se esperar que a atividade econômica esteja causando um dando menor pelo menos para os poluentes associados à atividade industrial.   À medida que o desenvolvimento e o progresso industrial avançam os danos ambientais também aumentam devido a maior utilização dos recursos naturais associados a aumentos nas emissões de poluentes. Isso ocorre devido à utilização de tecnologias menos eficientes e relativamente sujas, uma vez que a sociedade prioriza a competitividade de sua produção industrial e ignora os efeitos do crescimento econômico para o meio ambiente. À medida que o crescimento econômico e consequentemente a renda continuarem a se elevar, ocorrerão aumentos na expectativa de vida e surgirão novas demandas por água mais limpa, melhor qualidade do ar, entre outras, ou seja, um habitat mais limpo se torna mais valioso. (Yandle et al., 2002)

O impacto ambiental será uma função que assumirá formato de U invertido na renda per capita devido a alguns elementos, como a elasticidade positiva para a qualidade ambiental, de modo que esta se torna mais valorizada pela sociedade de acordo com o aumento da renda; alteração na composição da produção e do consumo; educação e conscientização ambiental; organismos políticos mais abertos. Outras possíveis causas são a liberalização comercial, mudanças tecnológicas positivas e maior rigidez das legislações ambientais.  (Almeida; Carvalho, 2010) De acordo com Thomas e Callan (2012) o modelo sugere que os estágios iniciais da industrialização estão relacionados com níveis crescentes de poluição, quando o crescimento é uma prioridade maior do que a proteção dos recursos. Também implica que o desenvolvimento mais avançado está ligado a uma mudança do foco na direção oposta, basicamente um efeito da renda e um fortalecimento concomitante das leis ambientais.

De acordo com De Bruyn et al (1998) e Almeida e Carvalho (2010), a curva de Kuznets Ambiental apresentaria o formato de U invertido apenas no início da relação entre crescimento econômico e pressão ambiental; chegaria um momento em que após um determinado nível de renda, ocorreria um novo ponto de inflexão e a trajetória da CKA volta a ser ascendente, assumindo um formato similar a um N, ou seja, a degradação ambiental tornaria a apresentar em altos níveis. 

Os efeitos que atuam sobre a relação de crescimento econômico e qualidade ambiental podem ser decompostos em efeito escala (conforme há aumento da produção, a pressão sobre o meio ambiente também tende a aumentar); efeito composição (o crescimento ocorre principalmente em setores com baixos níveis de emissão de poluentes); efeito técnico (um nível mais alto de produção é compensado pelos avanços tecnológicos, mantendo a qualidade ambiental quase inalterada). (Almeida; Carvalho, 2010; Stern, 2003)

O primeiro efeito pode ser anulado pelos outros dois efeitos, portanto, quando se analisa a CKA tem-se que tê-los em mente. Normalmente, nos países desenvolvidos a ocorrência do efeito escala sendo anula os outros dois efeitos, pois estes países possuem taxas de crescimento relativamente baixas. Já nós países em desenvolvimento, que possuem taxas de crescimento mais altas, normalmente o efeito escala não é completamente anulado pelos efeitos composição e técnico. (Almeida; Carvalho, 2010). A melhoria ambiental pode ser impulsionada por alterações na regulamentação ambiental, conscientização e educação no curso do desenvolvimento econômico. (Stern, 2003).

 As políticas do governo como regulamentações, taxas de poluição e a criação de permissões de emissões tornam-se um forte incentivo à mudança para processos de produção que gerem menores impactos ambientais, induzindo inovações ambientais endógenas. (Almeida; Carvalho, 2010).

3.  Procedimentos metodológicos

Esta seção está composta pela análise exploratória de dados espaciais; Autocorrelação Espacial Global Univariada e Bivariada; Autocorrelação Espacial Local Univariada e Bivariada; pelos modelos Econométrico-Espacial Clássico, SAR e SEM; e por testes que ajudam a identificar o melhor modelo a ser utilizado e os possíveis problemas existente no modelo.

A análise exploratória de dados espaciais (AEDE) de acordo com Almeida, Ferreira e Perobelli (2008) é fundamentada nos efeitos decorrentes da heterogeneidade espacial e da dependência espacial. Esta análise busca investigar a existência de distintos regimes espaciais, não-estacionariedade (instabilidade espacial) e identificar outliers (observações discrepantes), além de apresentar a distribuição espacial e os clusters espaciais (padrões de associação espacial). Costa, Dentinho e Nijkamp (2011) explicam que a dependência espacial é definida como a relação entre seus valores analisados em pontos relacionados (ou próximo) com o valor que toma uma variável num determinado ponto do espaço.

A AEDE utiliza a matriz de pesos espaciais (w), por meio da relação de vizinhança da distância geográfica ou/e socioeconômica. Anselin (1999) explica que os elementos da matriz de pesos estão embasados na contiguidade ou nos arranjos geográficos das observações. Portanto, a matriz objetiva captar a ponderação que determinada variável de cada região recebe quando vier a fazer vizinhança com a região analisada. Entre as matrizes de pesos espaciais, a utilizada nesta pesquisa é a denominada de Rainha (QUEEN). Almeida (2004) explica que ela aborda as fronteiras com extensões diferentes de zero. Na Figura 1 o quadrado a pode se avizinhar com os quadrados b, ou se avizinhar com os quadrados c, ou ambas as combinações podem ocorrer.

Figura 1 - Matriz "Rainha"
Fonte: DINIZ et al., 2014.

Para Autocorrelação Espacial Global Univariada O grau de combinação linear entre os vetores apresentados no tempo e os valores médios ponderados da vizinhança é fornecido pelo Índice de Moran, de acordo com Almeida, Ferreira e Perobelli (2008). A equação estatística do I de Moran é apresentada abaixo:

Para que haja similaridade entre os valores das variáveis consideradas é necessária a presença de autocorrelação espacial positiva. A existência de dissimilaridade entre os valores das variáveis apresentadas revela a presença de autocorrelação espacial negativa. (Almeida, 2004)

A Autocorrelação Espacial Local Univariada, de acordo com Almeida (2004), o I de Moran local é explicado pelo agrupamento dos valores similares da região estudada formando clusters espaciais, significativos estatisticamente. Para Anselin (1995) constata-se de uma decomposição do indicador global de autocorrelação em quatro categorias, onde cada uma representa um quadrante no diagrama de dispersão.

A estatística I de Moran local é apresentada pela seguinte equação (2):

Onde:  são variáveis padronizadas, a somatória de j é tal que unicamente os resultados dos vizinhos  são incluídos. O conjunto  agrega os vizinhos da variável i, por definição .

O diagrama de dispersão de Moran apresenta quatro padrões distintos de associações local espacial entre as regiões analisadas e sua vizinhança (Almeida, Ferreira, Perobelli, 2008). Nas regiões Baixo-Baixo do diagrama encontram-se agrupamentos que apresentam valores baixos e suas regiões também apresentam valores baixos. Já a região Alto-Alto do diagrama encontram-se agrupamentos que apresentam valores altos e suas regiões também apresentam valores altos. No quadrante Alto-Baixo, encontram-se agrupamentos que apresentam altos valores e que são cercados por regiões com baixos valores. Finalmente, no quadrante Baixo-Alto, encontram-se agrupamentos que apresentam baixos valores e que são cercados por regiões com altos valores. 

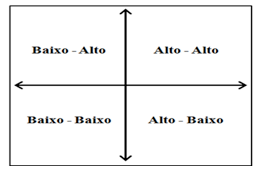
Fonte: DINIZ et al., 2014.
Figura 2 - Diagrama de dispersão

O objetivo da Autocorrelação espacial global bivariada é verificar se os valores observados em uma dada região guardam alguma relação com os valores observados de outra variável em regiões vizinhas, ou seja, se pretende verificar a existência de um padrão global entre duas variáveis diferentes, baseado em Almeida (2012). Para atingir tal objetivo necessário calcular a estatística I de Moran para duas variáveis diferentes padronizadas, digamos z1 e z2:

A expressão acima se transforma em,

Caso a matriz W seja normalizada na linha. O coeficiente possuíra dois componentes distintos. O numerado representará uma medida de covariância do tipo produto cruzado, o denominador se refere a um reescalonamento, utilizando a variância dos dados. A ideia é averiguar se existe uma associação linear entre a emissão de CO2 per capita e o PIB per capita.

A seguir apresenta-se a declividade da reta, onde α é a constante da regressão, β é o coeficiente angular e ε é um termo de erro aleatório.

Ao fazer o coeficiente angular da reta de regressão da defasagem espacial (Wz2) contra a variável z1 (de interesse), estimado pelo MQO (mínimo quadrados ordinários) obtém-se: 

No primeiro quadrante do diagrama de dispersão de Moran, situam-se os valores Alto-Alto (são as regiões com valores altos da variável de interesse no eixo das abscissas, circundados por regiões que também possuem valores altos da outra variável de interesse, está no eixo das ordenadas), no segundo quadrante têm os valores Baixo-Alto (são regiões com valores baixos da variável de interesse no eixo das abscissas, circunvizinhos por regiões com valores altos da outra variável), o terceiro quadrante apresenta os valores Baixo-Baixo (significa que os valores baixo de uma das variáveis são vizinhos dos valores baixo da outra variável) e o quarto quadrante exibe o agrupamento Alto-Baixo (neste os valores Alto da variável analisada estão rodeados pelos valores Baixo da outra variável).

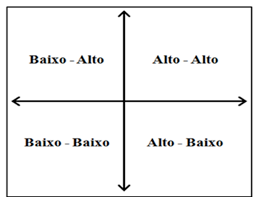
Fonte: Diniz et al.(2013)
Figura 3 - Diagrama de dispersão

O diagrama de dispersão bivariado, segundo Costa, Dentinho e Nijkamp (2011) permite representar sobre os eixos cartesianos a distribuição das duas variáveis geográficas, cuja relação desejamos conhecer. Da mesma forma, o GeoDa define uma recta de regressão que relaciona as duas variáveis analisadas, utilizando para tal um processo de ajustamento dos mínimos quadrados ordinários, que também permite apresentar no gráfico o valor da inclinação da recta ajustada. [...] A análise dos quatro quadrantes do diagrama de dispersão permite identificar as zonas com valores superiores ou inferiores à média em ambas as variáveis ou aqueles com valores superiores à média numa variável e inferiores noutra. (Costa, Dentinho E Nijkamp, 2001, p. 270 e 271) 

Para a Autocorrelação Espacial Local Bivariada, supondo a existência das variáveis de interesse xi e yi, padronizando-as estas, obtêm respectivamente z1 e z2. Assim a formula do I de Moran local será:

Modelo de Erro Autorregressivo Espacial (SEM) a dependência espacial é residual e se caracteriza pela estrutura autorregressiva de primeira ordem no termo de erro.  Este modelo se caracteriza por seu padrão espacial se manifestar no termo de erro é dado por efeitos não modelados por conta da falta de adequada medida, que não são distribuídos aleatoriamente no espaço, entretanto, ao contrario estão espacialmente autocorrelacionados. Os efeitos não modelados desta regressão não podem estar correlacionados com nenhuma das variáveis explicativas do modelo. (Almeida, 2012) A seguir a representação esquemática deste modelo SEM:

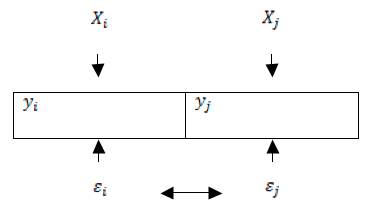
Fonte: Elaborado pelos autores com base em Almeida (2012)
Figura 6 - Processo de erro espacial

Na figura o erro da região j está correlacionado com o da região i. Portanto, no modelo SEM a dependência espacial se manifesta no termo de erro e não na variável dependente. (ALMEIDA, 2012) Abaixo apresenta-se formalmente o modelo SEM:

Costa, Dentinho e Nijkamp (2011) explicam que este modelo admite que exista autocorrelação no termo de erro, indicando que algo se passa em termos territoriais, entretanto não é possível identificar o porquê, ou seja, o modelo pode possuir outro tipo de erro de especificação ou se deve a existência de variáveis omissas no modelo. O modelo SEM mostrou-se adequado para averiguar o formato da CKA no curto e no longo prazo, no lugar do modelo clássico e de outros modelos espaciais, que apresentaram problemas em vários testes realizados em uma versão prévia deste artigo.

O teste do I de Moran difuso se apresenta como sendo um teste sobre a autocorrelação espacial dos resíduos da regressão. Assumindo inicialmente a seguinte forma:

A fórmula do teste é descrita a seguir:

De acordo com Almeida (2012):

[...] para pequenas amostras, Anselin e Rey (1991) descobriram que a estatística é robusta contra erros não normais, em especial para erros exponenciais e erros log-normais. Ademais, a estatística  mostra-se também robusta na presença de heterocedasticidade. Outra vantagem deste teste é a relativa facilidade computacional, já que, sob a hipótese nula, pode ser calculada com base nos resíduos de uma regressão estimada por MQO. Assim sendo, tal teste compartilha dessa vantagem com o I de Moran. A outra vantagem é a discriminação do tipo de autocorrelação espacial presente nos dados na forma de defasagem (Wy) ou de erro (W ). A grande desvantagem do teste é representada pela falta de poder que acarreta a frequência rejeição da hipótese nula, mesmo quando ela é verdadeira. (Almeida, p.223, 2012)

Nesse segmento com os dados da análise espacial a Curva de Kuznets Ambiental faz a relação entre pressão ambiental e nível de renda. Como o objetivo é verificar estatisticamente que existe relação entre essas variáveis, utiliza-se o PIB per capita e para a pressão ambiental escolhe-se uma variável medida globalmente e resultante da atividade humana a emissão de CO2 per capita.

Os dados foram coletados através do site do Banco Mundial (The World Bank, 2014), contendo 214 regiões. Às regiões que não possuíam valores para as duas variáveis foram atribuídos o valor zero. As amostras coletadas foram com relação ao PIB per capita dos países e suas emissões de CO2 cúbicas per capita. Os anos de 1994 e 2009 foram os selecionados para o estudo. As variáveis foram analisadas usando o programa Geoda. Somente foram analisadas as regiões que formaram estatisticamente significativamente e apresentaram relações de vizinhança formando clusters Alto-Alto e Baixo-Baixo. 

Os Dados e Modelo da Análise da Regressão Através do Geoda foram coletados através do site do Banco Mundial (The World Bank, 2014), contendo 214 regiões. Às regiões que não possuíam valores para qualquer uma das variáveis foi atribuído o valor zero para todas as demais. As variáveis foram analisadas usando o programa Geoda.

A análise se limitou a estudar as relações espaciais para uma possível existência da CKA para os anos 1994 e 2009. A variável ambiental dependente utilizada no modelo foi o dióxido de carbono per capita, por ser o principal responsável pelo efeito estufa e ser globalmente medido. As principais variáveis independentes utilizadas para a comprovação da CKA foi o PIB per capita, o PIB per capita ao quadrado e o PIB per capita ao cubo.

Além das variáveis independentes citadas acima, a analise do CO2 per capita foram incluídas as variáveis exportações per capita e o consumo de energia per capita. A especificação do modelo foi com base no apresentado por Almeida e Carvalho (2010) no trabalho "A hipótese da curva de Kuznets ambiental global: uma perspectiva econométrico-espacial". Caso alguma variável não possui valor para determinado país, está variável e as demais deste país receberam o valor zero, para evitar viesar os dados, que foram capitados através do site do Banco Mundial. 

A forma funcional do modelo de defasagem espacial com erro autorregressivo espacial apresenta o seguinte formato:

4 . Relação Mundial entre Renda e Emissão de Dióxido de Carbono

Este item discute inicialmente a relação espacial univariada e bivariada da emissão de dióxido de carbono per capita. Num segundo momento analisa-se a relação espacial entre emissão de gás carbônico per capita e PIB per capita. 

4.1 Relação Espacial Univariada da Emissão de CO2 Per Capita.

 As amostras coletadas foram com relação ao PIB per capita dos países e suas emissões de CO2 cúbicas per capita. Os anos de 1994 e 2009 foram os selecionados para o estudo. Somente foram analisadas as regiões que formaram estatisticamente significativas e apresentaram relações de vizinhança formando clusters Alto-Alto e Baixo-Baixo.  Os mapas foram obtidos através da analise exploratória de dados que busca investigar os padrões de associações espaciais (clusters).

Analisando a figura 3, o resultado indica a existência de autocorrelação espacial positiva para emissão de CO2 per capita cúbica para o ano de 1994 e 2009, ou seja, o I de Moran univariado é positivo (0,3437 e 0,3697 respectivamente) e este é maior que o I de Moran previsto (-0,004). Em outras palavras, o I de Moran é estatisticamente significativo, rejeitando-se a hipótese nula da aleatoriedade espacial. 

Fonte: Elaborado pelos autores através do programa GEODA
Figura 3 - Diagrama de dispersão e índices de Moran – 1994 e 2009

Ao comparar os I de Moran, nota-se que o ano de 2009 possui um I de Moran maior com relação ao ano de 1994. Tal resultado sugere que está havendo um aumento na relação de vizinhança espacial entre as regiões. Em outras palavras, a relação de emissão de CO2 cúbica per capita de uma dada região está tendo um maior impacto em outra dada região vizinha. Como os indicadores são significativos percebe-se também que a emissão de CO2 cúbica per capita apresenta concentração em determinadas áreas.

Na região Baixo-Baixo do diagrama acima se situam agrupamentos que apresentam valores baixos e suas regiões também apresentam valores baixos. Já as regiões Alto-Alto do diagrama encontram-se agrupamentos que apresentam valores altos e suas regiões também apresentam valores altos. Os valores encontrados para o I de Moran univariado obtido para emissão de CO2 per capita foram 0,3437 e 0,3697 respectivamente e revelam que na amostra os resultados concentram-se no primeiro quadrante (Alto-Alto) e terceiro quadrante (Baixo –baixo). Estão de acordo com a expectativa teórica da curva de Kuznets Ambiental, que prevê que nos estágios iniciais do desenvolvimento econômico as emissões de CO2 per capita são baixas dado o baixo nível de desenvolvimento, depois se elevam dado o aumento da produção e da renda per capita. O índice não permite identificar o padrão da curva, se linear (curtíssimo prazo), quadrática (curto e médio prazo) ou cúbica (longo prazo). A partir de certo nível as emissões de CO2 per capita irão começar a declinar com os aumentos na renda per capita, como resultados se tem que no curto prazo a CKA assumira o formato de U invertido.  

Na figura 4 em 1994 encontram-se dois clusters de CO2 per capita univariados Alto-Alto em 1994: (a) Polônia, Países Baixos, Noruega, Alemanha, Bélgica, Eslováquia e (b) Arábia Saudita, Omã e Emirados Árabes Unidos e o Canadá isolado. Foram identificados dois clusters Baixo-Baixo: (a) Guiné, Costa do Marfim, Burkina Faso e (b) Etiópia, Quênia, Tanzânia, Uganda, Zâmbia, Ruanda, República Democrática do Congo e República Centro Africana. Entende-se que essas áreas possuem baixas emissões de CO2 per capita e estão circundados por regiões com baixa emissão de CO2 per capita. A região branca do gráfico não apresentou valores significativos, enquanto a região cinza não apresentou relação de vizinhança.

Fonte: Elaborado pelo autor através do programa GEODA
Figura 4 - Mapa de Clusters da emissão per capita de CO2 do ano de 1994 e 2009

Em 2009, há dois clusters de CO2 per capita univariados Alto-Alto: (a) Alemanha e Bélgica e (b) Iraque, Arábia Saudita, Omã, Emirados Árabes Unidos e dois países isolados, Canadá e Rússia. Há também dois clusters Baixo-Baixo univariados na figura 4, as regiões que contemplam o primeiro cluster são Guiné, Costa do Marfim, Burkina Faso, Nigéria, Benim, Mali e Senegal e no segundo cliuster: Etiópia, Quênia, Tanzânia, Uganda, Zâmbia, Ruanda, República Democrática do Congo, República Centro Africana e Burandi.

4.2  Relação Espacial Bivariada entre Emissão de Gás Carbônico Per Capita e PIB Per Capita

Ao comparar os resultados obtidos de 1994 com 2009, percebe-se uma pequena mudança nas relações espaciais, portanto, as relações de autocorrelação entre as variáveis analisadas se alteram lentamente. Ou seja, a relação espacial entre emissão de CO2 cúbica per capita e PIB per capita se modificam pouco no tempo, resultando em clusters praticamente idênticos. No cluster Alto-Alto, por exemplo, houve a inclusão apenas do Reino Unido em 2009.

A figura 4 apresenta o índice Moran Global. Analisando o resultado para o ano de 1994, indica a existência de autocorrelação espacial positiva para emissão de CO2 per capita cúbica e o PIB per capita, ou seja, o I de Moran bivariado é positivo (0,2197) e este é maior que o I de Moran previsto (-0,004). Em outras palavras, o I de Moram é estatisticamente significativo, rejeitando-se a hipótese nula da aleatoriedade espacial.  A interpretação é que as regiões que apresentam elevada emissão de CO2 cúbica per capita tendem a estarem rodeadas por microrregiões vizinhas com um PIB per capita alto, as regiões com baixa emissão de CO2 cúbica per capita são vizinhas de microrregiões com baixa renda per capita (PIB per capita).

A análise da Figura 5 para o ano de 2009 indica a existência de autocorrelação espacial positiva para emissão de CO2 per capita cúbica e o PIB per capita, ou seja, o I de Moran bivariado é positivo (0,1778) e este é maior que o I de Moran previsto (-0,004). Em outras palavras, o I de Moram é estatisticamente significativo, rejeitando-se a hipótese nula da aleatoriedade espacial.  A interpretação é que as regiões que apresentam elevada emissão de CO2 cúbica per capita tendem a estarem rodeadas por microrregiões vizinhas com um PIB per capita alto, as regiões com baixa emissão de CO2 cúbica per capita são vizinhas de microrregiões com baixa renda per capita (PIB per capita).

Fonte: Elaborado pelo autor através do programa GEODA
Figura  5 - Diagrama de dispersão e Índice de Moram bivariado entre emissão de CO2 per capita cúbica e o PIB per capita- 1994 e 2009

No primeiro quadrante do diagrama de dispersão de Moran, situa-se os valores Alto-Alto (são as regiões com valores altos de emissão de CO2 cúbica per capita, no eixo das abscissas, circundados por regiões que também possuem valores altos da outra variável (PIB per capita), estão no eixo das ordenadas), no segundo quadrante temos os valores Baixo-Alto (são regiões com valores baixos de emissão de CO2 cúbica per capita no eixo das abscissas, circunvizinhos por regiões com valores altos da outra variável), o terceiro quadrante apresenta os valores Baixo-Baixo (significa que os valores baixo de emissão de CO2 cúbica per capita são vizinhos dos valores baixo do PIB per capita) e o quarto quadrante exibe o agrupamento Alto-Baixo (neste os valores Alto da variável analisada (de emissão de CO2 cúbica per capita) estão rodeados pelos valores baixo da renda per capita).

Ao comparar os I de Moran dos anos de 1994 e 2009, respectivamente 0,2197 e 0,1778, verifica-se que o ano de 1994 possui um I de Moran maior com relação ao ano de 2009. Tal resultado sugere que está havendo uma diminuição na relação espacial entre as regiões. Em outras palavras a relação de emissão de CO2 cúbica per capita e PIB per capita de uma dada região está tendo um menor impacto em outra dada região vizinha.

Como a estatística I de Moran bivariada apresentou valor significativo, aceita-se a hipótese da existência de relação entre a emissão de CO2 per capita e PIB per capita. Espera-se que o comportamento se assemelhe ao descrito pela curva de Kuznets Ambiental, que afirma que nos estágios iniciais do desenvolvimento econômico o aumento da renda leva a aumentos na poluição, entretanto, a partir de certo ponto a poluição começa a cair com os aumentos na renda, adquirindo formato de U invertido no curto e médio prazo e de N no longo prazo

Conforme a Figura 6, em 1994 há um cluster isolado com os países França, Itália, Suíça, Áustria, Alemanha, Países Baixos, Bélgica, Dinamarca, Reino da Noruega, Suécia e Finlândia, caracterizado por áreas que possuem elevadas emissões de CO2 per capita e estão rodeadas por regiões com elevada renda per capita. E o país isolado do Canadá. Existem três clusters bivariado Baixo-Baixo: (a) China e Índia; (b) Etiópia, Quênia, Tanzânia, Burundi, Ruanda, Uganda, Congo, e Benim e (c) Burkina Faso, Costa do Marfim e Guiné. Existe ainda uma relação Alto-Baixo para Coreia do Sul, o que significa uma relação de emissão de CO2 alta com uma renda per capita abaixo da média.

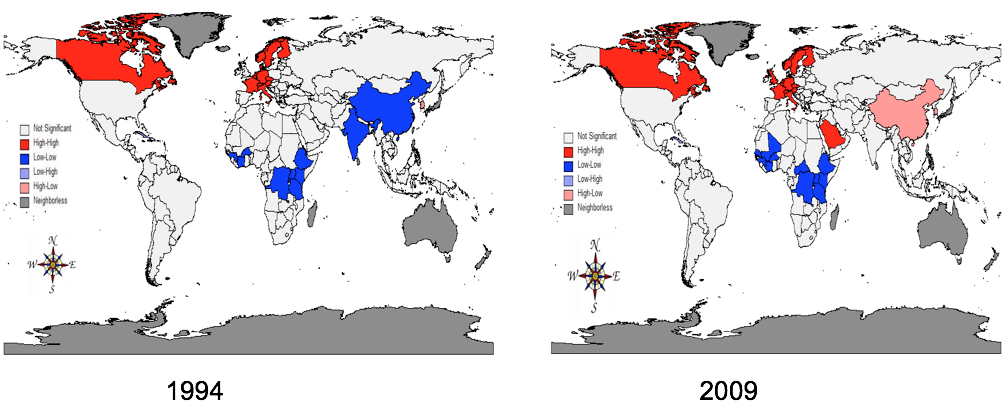
Fonte: Elaborado pelos autores através do programa GEODA
Figura 6 - Mapa de Clusters para a relação entre emissões de CO2 cúbica per capita e PIB per capita para o ano de 1994 e 2009

De acordo coma  Figura 6, em 2009 há cluster bivariado Alto-Alto envolvendo Reino Unido, França, Itália, Suíça, Áustria, Alemanha, Bélgica, Países Baixos, Noruega, Suécia e Finlândia.  Pode-se dizer que essas áreas possuem elevadas emissões de CO2 per capita e estão rodeadas por regiões com elevada renda per capita. Identificaram-se dois clusters bivariado Baixo-Baixo: (a) Etiópia, Uganda, Quênia, Ruanda, Tanzânia, Congo e Zâmbia; e (b) Burkina Faso, Mali, Costa do Marfim, Guiné e Senegal.  Existe ainda uma relação Alto-Baixo para Coreia do Sul e China, significando uma relação de emissão de CO2 elevada com uma renda per capita abaixo da média.

Como todos os indicadores do I de Moran apresentados anteriormente são significativos, sugerindo a existência de relação espacial entre as variáveis PIB per capita e CO2 per capita, portanto, este é mais indício da provável existência da curva de Kuznets ambiental. A análise de clusters revelou a presença de clusters alto-alto no Canadá e em europeus - França, Itália, Suíça, Áustria, Alemanha, Países Baixos, Bélgica, Dinamarca, Reino da Noruega, Suécia e Finlândia em 1994.  O formato da curva no curto prazo deverá ter um formato de U invertido, uma vez que os resultados apresentados pela análise univariada realizada no capitulo anterior mostra resultados que nos levam a essa conclusão.

3.2. Análise dos Resultados dos Modelos Espaciais

Os indicadores anteriormente analisados – índice Global de Moran univariado e bivariado apresentaram forte correlação espacial – e os dados da estimação da regressão  do CO2 per capita (variável dependente), contra o PIB per capita, PIB per capita ao quadrado, PIB per capita ao cubo, consumo de energia per capita e exportações per capita, pelo método dos mínimos quadrados ordinários, sem considerar a relação espacial presentou os problemas já esperados -.multicolinearidade entre moderada  e forte, teste Jarque Bera  e teste de Koenker-Basset confirma que os resíduos da regressão são homocedásticos. [6] Dada a presença  de tais problemas no modelo clássico, e a confirmação do teste do I de Moran difuso da presença de  relação espacial foram realizados os testes do multiplicador de Lagrange sendo todos significativos, menos o LM (multiplicador de Lagrange) Robusto lag que não apresentou valor significativo. O teste do multiplicador de Lagrange que apresentou os melhores resultados para o modelo foi LM Robusto error este, portanto, é o que melhor explica o modelo.

Tabela 2 - Modelo de Erro Espacial 1994 e 2009

Fonte: Elaboração dos autores com base no programa GEODA.

Para o ano de 1994, os coeficientes que foram significativos ao nível de significância de 1% são o PIB per capita, o PIB per capita ao quadrado, Lambda e o consumo de energia per capita. O coeficiente exportação per capita e o PIB per capita ao cubo foram significativos ao nível de significância de 5% e a constante não apresentou valor significativo. A variável dependente é explicada por 65% das variáveis independentes presentes no modelo, ou seja, o R² apresentou valor igual 0,65.

Os resultados da regressão estão de acordo com a expectativa teórica, com exceção da variável exportação per capita, e sugerem a existência de uma curva de Kuznets Ambiental no formato de U invertido no curto prazo e em uma perspectiva de longo prazo o modelo sugere uma provável existência da curva de Kuznets Ambiental no formato de N. Isso ocorre porque nos estágios iniciais o aumento da renda leva a aumentos na poluição, entretanto, a partir de certo ponto a poluição começa a cair com os aumentos na renda. Observa-se pelo modelo também que a queda da poluição não será para sempre, a partir de certo estagio novamente os níveis de poluição voltarão a se elevar.

O PIB per capita apresentou valor positivo, o que significa que esta variável impacta de forma positiva para o aumento das emissões per capita de CO2. As emissões de CO2 aumentarão conforme a renda aumenta, porém somente até certo ponto. Observamos que ao duplicar está variável, ela passa a receber sinal negativo, ou seja, o PIB per capita ao quadrado passa a impactar negativamente na emissão de CO2 per capita.  Portanto, no curto ela assumirá o formato de uma curva de U invertido. 

Finalmente, se estimou o PIB per capita ao cubo para verificar se os aumentos na renda continuariam indefinidamente provocando quedas na emissão de CO2, o resultado apresentado foi positivo indicando que novos aumentos na renda a partir de certo ponto fariam novamente a emissão de CO2 voltar a crescer para os dados  de 1994. Este fato no leva a entende que em um prazo maior a CKA assumiria um formato de N, como descrito na teoria acima. 

Em 1994, o coeficiente das exportações per capita apresentou valor positivo, sugerindo que existe uma relação positiva entre comércio internacional e emissões de CO2. Quando o esperado era que está variável apresenta-se sinal negativo. Porque a expectativa é que o comercio internacional ajude nas especializações das economias, o que significaria um menor consumo de energia e recursos naturais, de acordo com Stern et al  (1996), resultando em uma queda nas emissões de CO2 per capita.

 A variável consumo de energia também apresentou sinal positivo em 1994, significando que aumento nesta variável impacta positivamente no aumento das emissões de CO2. O sinal positivo assumido por esta variável já era esperado uma vez que as fontes produtoras de energia em grande parte emitem esse gás para gerar energia.  O valor positivo de 0,59 do coeficiente lambda é estatisticamente significativo e indica que existem variáveis que impactam a emissão de CO2 per capita, porém não são modeladas.

Para 2009 foram utilizados os testes do multiplicador de Lagrange sendo todos significativos, menos o LM (multiplicador de Lagrange) Robusto lag que não apresentou valor significativo. O teste do multiplicador de Lagrange que apresentou os melhores resultados para o modelo foi LM Robusto error este, portanto, é o que melhor explica o modelo. Os coeficientes que foram significativos ao nível de significância de 1% são o PIB per capita, o PIB per capita ao quadrado, PIB per capita ao cubo e Lambda. O coeficiente exportação per capita, o coeficiente consumo de energia per capita e a constante não apresentaram valor significativo.  A variável dependente é explicada por 66% das variáveis independentes presentes no modelo, ou seja, o R² apresentou valor igual 0,66.

Os resultados significativos da regressão para 2009 estão de acordo com a expectativa teórica e sugerem a existência de uma curva de Kuznets Ambiental no formato de U invertido no curto prazo e em uma perspectiva de longo prazo a existência da curva de Kuznets Ambiental no formato de N. Isso ocorre porque nos estágios iniciais o aumento da renda leva a aumentos na poluição, entretanto, a partir de certo ponto a poluição começa a cair com os aumentos na renda. Percebe-se pelo modelo também que a queda da poluição não será para sempre, a partir de certo estágio novamente os níveis de poluição voltarão a se elevar.

EM 2009, encontra-se o valor positivo de 0,59 do coeficiente lambda e ele é estatisticamente significativo indicando que existem variáveis que impactam na emissão de CO2 per capita, porém não são modeladas. As variáveis consumo de energia per capita e exportações per capita não apresentaram valores significativos para a nossa análise, por isso não podemos realizar inferências sobre elas, devido a grande chance de erro. O coeficiente PIB per capita apresentou valores positivos, o que significa que está variável impacta de forma positiva para o aumento das emissões per capita de CO2. As emissões de CO2 aumentarão conforme a renda aumenta, porém somente até certo ponto. Observamos que ao duplicar está variável, ela passa a receber sinal negativo, ou seja, o PIB per capita ao quadrado passa a impactar negativamente na emissão de CO2 per capita.  Portanto, no curto ela assumirá o formato de uma curva de U invertido. 

Por fim, se estimou o PIB per capita ao cubo para verificar se os aumentos na renda continuariam indefinidamente provocando quedas na emissão de CO2, o resultado apresentado foi positivo indicando que novos aumentos na renda a partir de certo ponto fariam novamente a emissão de CO2 voltar a crescer. Este fato permite inferir que em um prazo maior a CKA assumiria um formato de N, como descrito na teoria acima.

A hipótese da existência de uma curva de Kuznets global é aceita tanto para o ano de 1994 como para o ano de 2009, devido ao fato que nestes dois anos analisados os sinais dos coeficientes se comportaram de maneira esperada. Como PIB per capita apresentou valores positivos implica que está variável impacta de forma positiva para o aumento das emissões per capita de CO2 nos dois anos. Entendemos que as economias nos estágios iniciais, aumentos na renda levam a aumentos nas emissões de CO2 per capita, isso ocorre de acordo com a teoria por causa da pobreza que limita o país na adoção técnicas usadas durante o processo produtivo para conter os agentes poluidores.

 Ao elevar ao quadrado o PIB per capita para os dois anos, ele passa a receber sinal negativo, ou seja, o PIB per capita ao quadrado passa a impactar negativamente na emissão de CO2 per capita.  Esse resultado está de acordo com a teoria da CKA e no curto ela assumirá o formato de uma curva de U invertido. Isso ocorre porque a partir de certo com o crescimento da renda a pobreza já não é um fator tão limitante quanto nos estágios iniciais, o país agora passa a dar mais atenção ao meio ambiente e novas técnicas e leis são implementadas pela sociedade na produção de riquezas. 

A teoria da CKA nos diz que em certo momento ocorrerá um novo ponto de inflexão e a curva voltará a ser ascendente. Portanto, estima-se o PIB per capita ao cubo para verificar se os aumentos na renda continuariam indefinidamente provocando quedas na emissão de CO2, o resultado apresentado foi positivo para os dois períodos analisados indicando que novos aumentos na renda a partir de certo ponto fariam novamente a emissão de CO2 voltar a crescer. Este fato no leva a entende que em um prazo maior a curva de Kuznets ambiental assumiria um formato de N.

O coeficiente consumo de energia per capita deverá assumir valor positivo tanto para o ano de 1994 e 2009, porque teoricamente aumentos no consumo de energia devem aumentar a emissão do dióxido de carbono, uma vez que as fontes produtoras de energia em grande parte emitem esse gás para gerar energia, de acordo com Almeida e Carvalho (2010). Para o ano de 1994 esse resultado esperado é obtido, entretanto para o ano de 2009 ele é obtido somente para o modelo clássico, no modelo de erro espacial apesar do sinal estar de acordo com a teoria o valor obtido não é estatisticamente significativo.

Finalmente, para Stern et al., (1996), alterações nas estruturas das economias e as modificações dos padrões internacionais de qualidade ambiental induzirão os países a se especializarem em atividades que consumam menos recursos naturais e energia, portanto, espera-se que a variável exportações per capita  assuma um valor negativo. Como se observa nos períodos analisados não se obtivem os coeficientes com os sinais esperados para está variável. No ano de 1994 todos os períodos foram significativos a algum nível de significância, mostrando que o comércio internacional eleva as emissões de CO2 per capita. Já no ano de 2009, os coeficientes desta variável não foram estatisticamente significativos.

5. Considerações Finais

A teoria da curva de Kuznets descreve a trajetória da poluição de um estado como resultado do seu desenvolvimento econômico em dado período de tempo. A CKA deverá assumir o formato de "U" invertido no curto prazo, uma vez que está prevê que nos estágios iniciais do desenvolvimento econômico o crescimento da renda provocará a degradação ambiental, mas somente até certo momento, depois os aumentos na renda farão com que tal degradação comece a diminuir.

Portanto, o objetivo foi buscar elementos que poderiam comprovar a existência de relação entre emissão de CO2 e o crescimento da renda e também averiguar o formato da curva de Kuznets Ambiental. Os I de Moran bivariados foram significativos, indicando relação espacial entre as variáveis analisadas e as regressões indicaram que a CKA assumirá um formato de U invertido no curto prazo e de N no longo prazo.

O primeiro objetivo específico foi verificar a existência de relação espacial entre emissão de CO2 per capita e PIB per capita através da estatística I de Moran. Como a mesma apresentou valor elevado e foi significativa consegue-se afirmar que existe relação espacial entre essas duas variáveis. O Protocolo de Kyoto provavelmente foi um dos fatores capazes de promover modificações no cenário dos mapas principalmente onde se concentra os países presentes no anexo I que tem metas obrigatórias, no caso principalmente a Europa.

Após verificar através dos mapas e da estatística I de Moran a existência de relação espacial entre as variáveis CO2 per capita e PIB per capita. Busca-se através da regressão averiguar o formato da curva de Kuznets ambiental de acordo com a teoria econômica e este foi o último objetivo especifico alcançado. Para comprovar a hipótese da CKA na forma de U invertido era necessário que o coeficiente PIB per capita seja positivo e significativo, ao passo que o coeficiente PIB per capita ao quadrado apresente sinal negativo e ser significativo. Para verificar se os aumentos de renda manterão as quedas nas emissões de CO2 constante se estimou o PIB per capita ao cubo, caso seja significativo e apresente sinal positivo, isso implicará em evidencias de que a CKA em um prazo de tempo maior possuirá um formato de N.  A hipótese da existência de uma curva de Kuznets global é aceita tanto para o ano de 1994 como para o ano de 2009, devido ao fato que nestes dois anos analisados os sinais dos coeficientes se comportaram de maneira esperada. Indicando uma provável existência da CKA no formato de U invertido no curto prazo e no longo prazo a CKA assumiria um formato de N.

Referências

ALMEIDA, E.; CARVALHO, T. S. A hipótese da curva de Kuznets ambiental global: uma perspectiva econométrico-espacial. (Escrito em: 09/2010). Disponível em:<http://www.scielo.br/scielo.php?pid=S0101-1612010000300004&script=sci_ arttext>. Acessado em: 26/11/2013.

ALMEIDA, E. (2204) Curso de Econometria Espacial Aplicada. ESALQ-USP: Piracicaba.

ALMEIDA, E.(2012). Econometria espacial aplicada. Campinas, SP: Editora Alínea.

ALMEIDA, E. S.; FERREIRA P. G. C.; PEROBELLI, F. S. Existe convergência espacial da produtividade agrícola no Brasil?RER, Rio de Janeiro, vol. 46, n. 01, p. 031-052, jan/mar 2008.

ANSELIN, L. (1999). Spatial Econometrics. Universidade do Texas em Dallas, Escola de Ciências Sociais, 26 de abril.

ANSELIN, L. (1995). Local Indicators of Spatial Association – LISA. Geographical Analysis, 27, n. 2, p. 93-115

ARRAES, R. A.; DINIZ, Marcelo B.; DINIZ, Márcia J. T. Curva ambiental de Kuznets e desenvolvimento econômico sustentável. (Escrito em: 2006). Disponível em:<http://www.scielo.br/scielo.php?pid=S0103-20032006000300008&script=sci_ arttext>. Acessado em: 25/11/2013.

ARROW, et al. Economic growth, carrying capacity, and the environment. Science n.268, 520–521. 1995. Disponível em: <http://www.precaution.org/lib/06/econ_growth_and_ carrying_capacity.pdf>. Acessado em: 22/11/2009.

BANCO MUNDIAL. Disponível em: < http://data.worldbank.org/indicator/all >. Acessado em: 26/11/2013.

BRASIL. MMA, Ministério do Meio Ambiente do Brasil. (1997).  Protocolo de Quioto. Disponível em: http://www.mma.gov.br/clima/protocolo-de-quioto. Acessado em: 13/11/2013.

CMMAD. Comissão Mundial Sobre Meio Ambiente E Desenvolvimento. (1988). Nosso Futuro Comum. Rio de Janeiro: FGV, 1988.

COSTA, J. S; DENTINHO, T. P; NIJKAMP, P. (2011). Compêndio de Economia Regional. Cascais: Princípio.

DE BRUYN, S. M.; VAN DEN BERGH, J. C. J. M.; OPSCHOOR, J. B. (1998). Economic Growth and Emissions: reconsidering the empirical basis of environmental Kuznets curves. Ecological Economics, Amsterdam, vol. 25, p. 161-175.

DINIZ, S. S.; CÂMARA, M. R. G.; MASSAMBANI, M. O.; ANHESINI, J. A. R.; FILHO, A. S., Análise espacial da produtividade da laranja dos municípios do estado de São Paulo: 2002-2010. In: Sociedade Brasileira de Economia Administração e Sociologia Rural. Disponível em: <http://www.sober.org.br/?op =paginas&tipo= secao&secao=7&pagina=7>. Acessado em: 10/04/2014.

GUJARATI, D; (2006). Econometria Básica. Rio de Janeiro: Elsevier. 

LOMBORG, B. (2002). O Ambientalista Cético. Rio de Janeiro: Elsevier.

RATTNER, H. (1999). Liderança para uma sociedade sustentável. São Paulo: Nobel.

STERN, D. I; COMMON, M. S; BARBIER, E. B. (1996). Economic Growth and Environmental Degradation: The Environmental Kuznets Curve and Sustainable Development. World Development, vol. 24, n. 7, p. 1151-1160.

STERN, D.I; (06/2003). The Environmental Kuznets Curve. Disponível em: http://isecoeco.org/pdf/stern.pdf. Acessado em: 10/11/2014.

THOMAS, J. M; CALLAN. S. J. (2012). Economia Ambiental. São Paulo: Cengage Learning.

UNFCCC, United Nations Framework Convention on Climate Change.  Clean Development Mechanism (CDM). Disponível em: http://unfccc.int/kyoto_protocol/mechanisms/clean_development_mechanism/items/2718.php. Acessado em: 08/08/ 2014 - A.

UNFCCC, United Nations Framework Convention on Climate Change. International Emissions Trading. Disponível em:  http://unfccc.int/kyoto_protocol/mechanisms/emissions_trading/items/2731.php. Acessado em: 08/08/2014 - B.

UNFCCC, United Nations Framework Convention on Climate Change. Joint Implementation (JI). Disponível em: http://unfccc.int/kyoto_protocol/mechanisms/joint_implementation/items/1674.php. Acessado em: 08/08/2014 - C.

YANDLE B; VIJAYARAGHAVAN, M; BHATTARAI M. (05/2002). The Environmental Kuznets Curve: A Primer. Disponível em: http://www.macalester.edu/~wests/econ231/yandleetal.pdf . Acessado em: 05/12/2014. 

ANEXO

Tabela  A1 - Modelo Clássico 1994 e 2009

Fonte: Elaboração dos autores com base no programa GEODA.

1. Mestre, Universidade Estadual de Londrina – UEL. E-mail: fernandoartico@yahoo.com.br
2. Doutora, Economia, Universidade Estadual de Londrina, Londrina - UEL, PR, Brasil E-mail: zapparoli@uel.br

3. Doutor,Coordenador de Economia Regional, Universidade Estadual de Londrina, Londrina - UEL, PR, Brasil. E-mail: umasesso@uel.br

4. Doutor, Universidade Estadual Norte do Paraná – UENP, Cornélio Procópio, PR, Brasil. E-mail: paulobrene@uenp.edu.br

5. Doutora, Universidade Estadual de Londrina, Londrina - UEL, PR, Brasil E-mail: mgabardo@uel.br

6. Os testes apresentados neste parágrafo e os resultados do regressão via MQO podem ser encontrados no Anexo .