HOME | ÍNDICE POR TÍTULO | NORMAS PUBLICACIÓN

Espacios. Vol. 37 (Nº 02) Año 2016. Pág. 2

Análise da Eficiência Econômica na Produção de Vinhos do Rio Grande do Sul

Analysis of the Economic Efficiency of Rio Grande do Sul Wine Production

Paulo Henrique de Oliveira HOECKEL 1; Clailton Ataídes de FREITAS 2

Recibido: 01/09/15 • Aprobado: 22/09/2015

Contenido

1. Introdução

2. Aspectos teóricos da economia da produção

3. Metodologia

4. Resultados e discussões

5. Conclusão

Referências

1. Introdução

Atualmente, a área de produção vitivinícola no Brasil é de 83,7 mil hectares, divididos, principalmente, entre seis regiões [3]. São mais de 1,1 mil vinícolas espalhadas pelo país, a maioria instalada em pequenas propriedades (média de 2 hectares por família). A vitivinicultura brasileira está concentrada substancialmente no Rio Grande do Sul. Segundo a Academia do Vinho [4], esse estado respondeu por, aproximadamente, 90% da produção de vinho brasileiro [5] e abriga as principais entidades ligadas à busca por melhorias do vinho brasileiro, como a UVIBRA (União Brasileira de Vitivinicultura) e a ABE (Associação Brasileira de Enologia). Além disso, o estado conta com, aproximadamente, vinte mil famílias de agricultores direta e indiretamente ligados à produção de uva.

Os principais problemas enfrentados pela vitivinicultura gaúcha e, consequentemente, a brasileira são, primeiro, a competição com os vinhos estrangeiros, cuja qualidade e baixo preço ameaçam o mercado de vinhos de mesa no Brasil; segundo, o restrito consumo de vinho no mercado interno de, aproximadamente, dois litros per capita/ano [6]. Esse baixo consumo se deve aos fatores culturais, ao baixo poder aquisitivo do brasileiro e ao preço do vinho nacional, relativamente mais caro, vis-à-vis o importado.

Mesmo com a vitivinicultura tendo importância em termos sociais e culturais para a economia gaúcha, os estudos realizados dentro do setor vinícola estão mais ligados às questões técnicas, como a qualidade do vinho e as melhores formas de produzi-lo, aos fatores enológicos, aos tipos de uvas usadas na produção e à dinâmica estrutural do setor. Além disso, existe também um número ainda limitado de estudos a respeito do dinamismo econômico. Dessa forma, pôde-se verificar que ainda existe uma carência de pesquisa destinada a analisar a eficiência econômica deste setor.

Neste sentido, a consecução da presente pesquisa busca contribuir com as análises deste setor, objetivando alavancar e incitar novos estudos econômicos que possam complementar esta lacuna, para que seja possível compreender melhor a realidade desse setor no que se refere à eficiência das unidades vinícolas do Rio Grande do Sul.

De acordo com Gomes e Mangabeira (2004), a eficiência de uma unidade produtiva é medida através da comparação entre os valores observados e os valores ótimos de seus produtos (saídas) e recursos (insumos). Esta comparação pode ser feita, em linhas gerais, pela razão entre a produção observada e a produção potencial máxima alcançável, dados os recursos disponíveis; ou pela razão entre a quantidade mínima necessária de recursos e a quantidade efetivamente empregada, dada a quantidade de produtos gerados.

Com o intuito de realizar a mensuração dessas medidas de desempenho através do envelopamento dos dados, limitados por regiões (fronteiras) de máxima produção ou de mínimo custo, o presente estudo faz uso da modelagem que envolve a programação matemática, sendo tais modelos denominados como modelos de Análise Envoltória de Dados (DEA) [7].

Há várias utilizações da DEA na agricultura brasileira, conforme indica a literatura da área e entre as mais recentes, cabe destacar: Gomes e Mangabeira (2004), Magalhães e Campos (2006), Ferreira e Braga (2007), Pereira C. N. (2012), Vicente (2012) e Carlucci (2012). Na literatura internacional, tem-se Zofio e Lovell (2001), Krasachat (2002), De Koeijer et al. (2002), Lansink et al. (2002), Monchuk e Chen (2008), Asogwa et al. (2011), porém nenhum destes estudos engloba o setor vinícola.

Desta forma, a consecução da presente pesquisa avança com relação aos trabalhos existentes na literatura, ao verificar se as empresas vinícolas do Rio Grande do Sul possuem eficiência econômica relativa na produção de vinhos, recorrendo ao approach da teoria da produção e com o auxílio do ferramental da DEA. Isto é, este estudo permite analisar os efeitos de escala e diagnosticar, dentro da amostra, quais vinícolas são eficientes e quais são ineficientes, ou quais variáveis precisam de ajustes para que a vinícola se torne mais eficiente, agregando, assim, conhecimento teórico ainda não explorado em relação ao tema proposto.

Nesse sentido, o problema de pesquisa do presente estudo pode ser encerrado com um questionamento básico: dada a amostra das vinícolas gaúchas, quais dessas empresas podem ser consideradas eficientes, através do método DEA?

Como hipótese de estudo tem-se que a maior parte das vinícolas amostradas opera de forma eficiente, considerando que o setor vinícola de modo geral vem buscando se modernizar para fazer frente aos vinhos importados.

Para responder ao problema de pesquisa, delineia-se como objetivo geral: analisar a eficiência econômica na produção de vinhos do Rio Grande do Sul para o ano/safra 2008/2009 através da DEA, utilizando uma amostra estatisticamente representativa das vinícolas gaúchas legalmente cadastradas no IBRAVIN. Especificamente, busca-se avaliar os resultados obtidos quanto à eficiência alocativa, técnica e econômica das vinícolas, interligando-os com a realidade econômica do setor.

Este artigo está organizado em seis seções, a saber: a primeira contempla os objetivos do estudo e a contextualização do problema de pesquisa; na segunda seção é apresentado o referencial teórico com base na teoria da produção; a terceira seção apresenta a metodologia desenvolvida, a partir da coleta de dados, e a modelagem DEA; a quarta seção consiste na apresentação e análise dos resultados obtidos; na quinta e última seção delineia-se a conclusão a respeito das discussões propostas e dos resultados obtidos, contrapondo-os com a realidade econômica do setor estudado.

2. Aspectos teóricos da economia da produção

O presente trabalho tem a chamada "teoria da produção" como instrumento teórico para analisar o processo produtivo do vinho. Para tanto, utilizam-se os elementos teóricos da função de produção, do conceito de produtividade e de eficiência econômica, descritos a seguir, assim como os demais conceitos e técnicas utilizados ao longo da presente pesquisa.

Segundo Thompson e Formby (2003), qualquer atividade que cria valor pode ser considerada produção. O termo produção abrange, portanto, todas as atividades econômicas associadas ao fornecimento de bens ou serviços para o usuário final. Ainda segundo os autores, em termos gerais, a produção consiste em uma série de atividades pelas quais os insumos produtivos (matérias-primas, trabalho, tecnologia, capital, utilização da terra e talento empresarial) são usados para gerar produção de bens e serviços.

Segundo Mas-Collel et al. (1995), em uma economia com L commodities, um vetor de produção (ou plano de produção) é um vetor , que descreve os resultados (líquidos) das mercadorias L, a partir de um processo de produção. Alguns elementos de um vetor de produção podem ser zero, indicando que o processo não tem produto líquido dessa commodity. Ainda para esses autores, para analisar o comportamento da empresa, é preciso começar identificando os vetores de produção que são tecnologicamente possíveis. O conjunto de todos os vetores que constituem planos de produção viáveis para a empresa é conhecido como o conjunto de produção e é denotado por . Qualquer  é viável, e qualquer   não é possível. O conjunto de produção é tomado como ponto de referência primitivo da teoria.

Thompson e Formby (2003) indicam que os insumos produtivos podem ser classificados em fixos ou variáveis. Um insumo fixo é definido como aquele cuja quantidade não pode ser alterada a curto prazo em um esforço para se alterar a quantidade de bens que se produz, como exemplos se têm equipamentos e máquinas, edifícios e o conhecimento gerencial dos administradores da firma. O insumo variável é aquele cuja quantidade pode ser rapidamente alterada caso se deseje aumentar ou diminuir o volume de produção, tais como: energia elétrica, a maior parte das matérias-primas, os serviços de transportes e a força de trabalho.

Visto que as empresas podem transformar, de várias maneiras, os insumos em produtos, usando diferentes combinações de mão de obra, matérias-primas e capital, pode-se descrever a relação entre os insumos do processo produtivo e o produto resultante como uma função de produção. Logo, uma função de produção indica o produto máximo (volume de produção), y, que uma empresa produz para cada combinação específica de insumos.

Se a função de produção é dada por  e se todos os insumos são multiplicados pela mesma constante positiva   (onde ), então, é possível classificar os retornos de escala da função de produção, como retorno de escala constante, decrescente ou crescente, conforme reage a produção diante do incremento dos insumos. A produtividade de uma unidade de produção, ou no presente caso de uma vinícola, é a relação entre os produtos (outputs) e os insumos (inputs). De acordo com Gomes, Soares de Mello e Biondi Neto (2003), no caso mais geral onde existem vários insumos e vários produtos, ou seja, a unidade emprega em seu processo de produção múltiplos insumos, que produzem múltiplos produtos, a produtividade é definida como a combinação linear dos produtos dividido pela combinação linear dos insumos.

De acordo com Mas-Collel et al. (1995), um vetor de produção  é eficiente se não houver , de tal modo que  e . Em outras palavras, um vetor de produção é eficiente se não houver outro vetor de produção viável​​ que gere tanto de um produto y, sem usar insumo adicional e que, efetivamente, produza mais de algum produto, ou utilize menos de algum insumo.

Para Thompson e Formby (2003), no longo prazo, a concorrência e a motivação do lucro induzem as firmas a investirem na tecnologia de produção mais eficiente disponível. No entanto, a curto prazo, a firma é obrigada a utilizar a tecnologia de produção de que dispõe, de forma a tentar obter a produção máxima que pode conseguir a partir da combinação de insumos escolhida.

A definição proposta por Farrel (1957) para a eficiência econômica, e assumida como base neste estudo, diz que a eficiência econômica total é a combinação das medidas de eficiência técnica, que reflete a habilidade da firma em obter máximo produto (dado um conjunto de insumos), e a eficiência alocativa, que reflete a habilidade da firma em utilizar os insumos em proporções ótimas (dados seus preços relativos) [8]. Logo, a medida de eficiência relativa de uma firma é determinada pela comparação da produção observada nessa firma, dado um conjunto de insumos, com a produção "ideal", com os mesmos níveis de insumos.

Segundo Figueiredo (2005), outro conceito importante é a eficácia que é definida como a relação entre os resultados obtidos e os resultados desejados ou previstos, sem levar em conta os recursos utilizados. Ou seja, nesse contexto, ser eficaz é fazer com que uma combinação de insumos atinja plenamente os resultados esperados.

A estimação de fronteiras de produção, conforme Gomes et al. (2003), possibilita a reflexão da tecnologia utilizada, isto é, a estimativa de uma fronteira de produção é influenciada pelas unidades de melhor desempenho relativo dentro da amostra de unidades analisada.

3. Metodologia

3.1 A aplicação da Análise Envoltória de Dados (DEA)

De acordo com Gomes e Baptista (2004), a DEA é uma abordagem não-paramétrica, que envolve programação matemática em seu processo de estimação. Trata-se, assim, de um método baseado em programação linear, cujo objetivo é medir a eficiência de entidades denominadas de DMUs [9] de maneira comparativa, tendo como base as informações dos recursos (inputs) e dos produtos (outputs) de cada DMU.

Segundo Charnes et al. (1994), a DEA envolve um princípio alternativo para extrair informações sobre uma população de observações. Ao contrário das abordagens paramétricas convencionais, cujo objetivo é estimar uma (hiper) superfície de regressão através dos dados, a DEA otimiza cada observação individual com o objetivo de calcular uma fronteira discreta por partes formada pelas unidades Pareto eficientes.

Na literatura, pode se encontrar a técnica DEA em muitas formas de aplicação. Esta pode variar quanto à orientação do modelo (minimizar inputs ou maximizar outputs), a forma dual ou primal do modelo de programação linear (envelope ou multiplicativa, respectivamente), quanto aos retornos de escala (constantes ou variáveis), quanto ao tipo de variáveis utilizadas (inteiras, binárias, categóricas, de intervalo, etc.), entre outras.

Os dois modelos mais conhecidos de DEA são o CCR (CHARNES; COOPER; RHODES, 1978) e o BCC (BANKER; CHARNES; COOPER, 1984). O modelo CCR trabalha com retornos constantes à escala e BCC considera retornos variáveis à escala, ou seja, substitui o axioma da proporcionalidade pelo axioma da convexidade. Tradicionalmente, são possíveis duas orientações radiais para esses modelos na busca da fronteira de eficiência: orientação a inputs e orientação a outputs [10].

Segundo Gomes e Baptista (2004), a DEA é uma ferramenta muito útil para analisar a eficiência de unidades. No entanto, é preciso que se tenha consciência de suas restrições, mas também é importante conhecer suas vantagens em comparação com os outros métodos [11].

3.2 Descrição da técnica da Análise Envoltória de Dados (DEA)

O marco inicial dos estudos sobre DEA pode ser encontrado em Farrell (1957), que propôs um modelo empírico para eficiência relativa, em oposição ao modelo de produção funcional teórico para eficiência. Com base nesse estudo, Charnes et al. (1978) propuseram uma abordagem não paramétrica para análise de eficiência com múltiplos inputs e múltiplos outputs. Essa abordagem tornou-se conhecida como DEA (VILELA et al. 2007).

A DEA otimiza cada observação individual com o objetivo de calcular uma fronteira de eficiência, determinada pelas unidades que são Pareto eficientes. O objetivo primário da DEA consiste em comparar um certo número de DMUs, que realizam tarefas similares e se diferenciam nas quantidades de inputs que consomem e de outputs que produzem (GOMES et al. 2001). De acordo com Gomes et al. (2003), pode-se definir os modelos DEA multidimensionais considerando os casos clássicos CCR e o BCC.

Para Soares de Mello et al. (2005), o modelo CCR desenha uma superfície não paramétrica linear por partes envolvendo os dados. Trabalha com retornos constantes de escala. Dessa forma, qualquer variação nas entradas (inputs) produz variação proporcional nas saídas (outputs).

Com base na metodologia desenvolvida [12] em Charnes et al. (1994), Gomes e Baptista (2004) e Coelli et al. (2005), pode-se iniciar a formalização do modelo DEA considerando a existência de k insumos e m produtos para cada n DMUs. Assim, são construídas duas matrizes - a matriz X de insumos, de dimensões (k x n), e a matriz Y de produtos, de dimensões (m x n), representando os dados de todas as n DMUs, como:

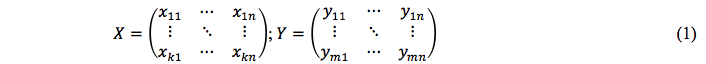
Na matriz X, cada linha representa um insumo e cada coluna representa uma DMU. Já na matriz Y, cada linha representa um produto e cada coluna uma DMU. Para a matriz X, são necessários que os coeficientes sejam não-negativos e que cada linha e cada coluna contenha, pelo menos, um coeficiente positivo, isto é, cada DMU consome ao menos um insumo, e uma DMU, pelo menos, consome o insumo que está em cada linha. O mesmo raciocínio se aplica para a matriz Y, ou seja, os coeficientes são não-negativos, cada produto é gerado ao menos por uma DMU e cada DMU produz pelo menos um produto.

 Pode-se, então, obter uma medida de eficiência para cada DMU da amostra, que é a razão entre todos os produtos e todos os insumos, matematicamente representado como:

em que,  e  são os vetores para insumos e produtos, respectivamente, para a i-ésima DMU;  é um vetor (m x 1) de pesos nos produtos e  é um vetor (k x 1) de pesos nos insumos.

O modelo adaptado de Charnes et al. (1978), para calcular a eficiência da i-ésima DMU, possui a seguinte forma:

Essa formulação envolve a obtenção de valores para  e , de tal forma que a medida de eficiência para a i-ésima DMU seja maximizada, sujeita à restrição de que as medidas de eficiência de todas as DMUs sejam menores ou iguais a um. A característica principal desse modelo é que os pesos  e  são tratados como incógnitas, sendo escolhidos de maneira que a eficiência da i-ésima DMU seja maximizada. Caso a eficiência obtida para a DMU que está sendo testada seja igual a um, ela será eficiente em relação às demais; caso contrário, ineficiente, pois, existem DMUs que combinam, de forma mais eficiente, os seus insumos e produtos.

Contudo, a restrição de não-negatividade imposta aos vetores de pesos não é matematicamente suficiente para obter um único valor definido. Isso porque, segundo Charnes et al. (1978), o modelo é originalmente uma programação não-linear estendida de um algoritmo de programação fracionário. Torna-se necessário, portanto, transformar o problema de programação fracionária, com infinitas soluções possíveis, em um problema de programação linear, com uma única solução. Essa transformação permite a utilização de um grande número de observações (DMUs) e um menor número de insumos e produtos, característica de muitas aplicações econômicas. A formulação linearizada é a seguinte:

O modelo apresentado na forma linearizada objetiva maximizar a produção virtual, mantendo a condição de que esta produção não exceda os insumos virtuais em nenhuma DMU. Nesse sentido, o modelo condiz com as condições de ótimo de Pareto, uma vez que incrementos no valor máximo somente são possíveis aumentando o valor de ao menos um insumo ou reduzindo a produção de algum produto (BOWLIN, 1998).

O problema anterior consiste em uma maximização do produto. Entretanto, por meio da dualidade em programação linear, pode-se derivar uma forma envoltória do problema anterior, a qual tem orientação insumo, da seguinte forma:

em que   é um escalar, cujo valor é a medida de eficiência da i-ésima DMU. Caso , a DMU será eficiente; caso contrário, será menos eficiente. O parâmetro  é um vetor (n x 1), cujos valores são calculados de forma a obter a solução ótima. Para uma DMU eficiente, todos os valores de  serão zero; para uma DMU ineficiente, os valores de  serão os pesos utilizados na combinação linear de outras DMUs eficientes, que influenciam a projeção da DMU ineficiente sobre a fronteira calculada. Isso significa que, para uma unidade ineficiente, existe pelo menos uma unidade eficiente, cujos pesos calculados fornecerão a DMU virtual da unidade ineficiente, mediante combinação linear. Essas unidades eficientes serão os benchmarks daquela DMU.

O modelo apresentado anteriormente busca identificar a ineficiência técnica das DMUs, mediante redução proporcional na utilização dos insumos, sendo, assim, um modelo com orientação insumo. No entanto, podem ser obtidas, também, medidas de eficiência com o aumento proporcional na produção, conhecidas como medidas de eficiência com orientação produto. Estas medidas permitem verificar qual a quantidade máxima que pode ser produzida, dada uma quantidade fixa de insumos. Assim, ao contrário dos modelos de insumo orientados, em que a ideia é reduzir os insumos, na orientação produto, os insumos são fixos e o produto pode ser expandido.

O problema com orientação produto, pressupondo-se retornos constantes, pode ser escrito da seguinte forma:

Para Coelli et al. (2005), o problema apresentado na forma envoltória (dual) envolve menor número de restrições do que o primal. Como no primal existem (k + m) variáveis, o dual terá (k + m) restrições, que é menor que as (n + 1) restrições do primal, uma vez que o número de DMUs é superior à soma do número de insumos mais o número de produtos. Nesse sentido, o dual é preferível ao primal, pois se consome menos tempo para ser resolvido. É importante destacar que o problema deve ser resolvido n vezes, isto é, uma vez para cada DMU na amostra.

Segundo Gomes e Baptista (2004), o modelo de retornos constantes a escala pode ser reformulado, com o objetivo de possibilitar retornos variáveis às DMUs analisadas. A ideia é introduzir uma restrição de convexidade ao modelo CCR apresentado na Equação (3). O modelo BCC pode ser representado pela seguinte notação algébrica:

em que  é um vetor (n x 1) de algarismos unitários (1,...,1).

O problema com orientação produto, pressupondo-se retornos variáveis, pode ser escrito da seguinte forma:

A abordagem de retornos variáveis forma uma superfície convexa de planos em interseção, a qual envolve os dados de forma mais compacta do que a superfície formada pelo modelo com retornos constantes. Com isso, os valores obtidos para a eficiência técnica, com a pressuposição de retornos variáveis, são maiores do que aqueles obtidos com retornos constantes. Se uma DMU é eficiente no modelo CCR, então ela também é eficiente no modelo BCC, pois, a medida de eficiência técnica obtida no modelo com retornos constantes é composta pela medida de eficiência técnica no modelo com retornos variáveis, também, chamada de pura eficiência técnica, pela medida de eficiência de escala e pela medida de congestão (SEIFORD; ZHU, 1999; FÄRE; GROSSKOPF, 2000).

O uso da especificação de retornos constantes, quando nem todas as DMUs estão operando em escala ótima, resulta em medidas de eficiência técnica que podem ser confundidas com eficiência de escala. Para separar essas medidas, realiza-se o procedimento, conduzindo ambos, retornos constantes e retornos variáveis, ao mesmo conjunto de dados. Se existir uma diferença nos valores de eficiência técnica para uma DMU qualquer, isso indica que esta DMU tem ineficiência de escala, que pode ser calculada pela diferença entre os valores das eficiências técnicas com retornos variáveis e com retornos constantes (GOMES; BAPTISTA, 2004).

Dessa forma, a medida de eficiência técnica com retornos constantes à escala é composta pela eficiência técnica pura e pela eficiência de escala:

em que ET é a medida de eficiência técnica; EEsc, a medida de eficiência de escala; o subscrito I indica modelos com orientação insumo; RC, retornos constantes; e RV, retornos variáveis.

O problema de minimização de custos para a i-ésima DMU, pressupondo-se retornos constantes à escala, é dado por:

em que  é o vetor de preço dos insumos para a i-ésima DMU e  é o vetor de insumos que minimiza os custos.

Obtida a composição ideal de insumos para a DMU e conhecendo os preços destes insumos, obtém-se o custo mínimo de produção. A medida de eficiência econômica (EE), para a i-ésima DMU, é dada pela razão entre o custo mínimo e o custo observado, sendo portanto:

Uma vez identificada a EE e conhecendo-se a eficiência técnica (ET), pode-se calcular, residualmente, a eficiência alocativa (EA) da seguinte forma:

Em um primeiro momento, define-se a escolha das DMUs que irão entrar na análise como objeto principal de pesquisa, as empresas vinícolas que fazem parte do sistema agroindustrial (SAI) [13] vitivinícola do Rio Grande do Sul, sendo a amostra de DMUs formada pelas vinícolas amostradas, legalmente cadastradas no IBRAVIN.

A aplicação dos modelos DEA, no presente estudo, foca-se na utilização dos insumos do processo produtivo do vinho, assumindo, desta forma, a orientação insumo. Sendo assim, a decisão primária é de regularizar a utilização dos insumos no processo produtivo das empresas do setor vinícola. Assim, são adotados os modelos CCR e BCC com orientação insumo para avaliar EE das empresas vinícolas (DMUs) ao decompô-la em ET e EA, além de analisar os efeitos de escala. Isso permite analisar mais detalhadamente o setor vinícola quanto ao funcionamento das vinícolas, de modo a avaliar se estas estão operando de forma eficiente economicamente.

Para realizar o processo de estimação dos modelos DEA propostos, utiliza-se o programa ISYDS - Integrated System for Decision Support (SIAD – Sistema Integrado de Apoio à Decisão). Utiliza-se a versão SIAD v.3.0 [14], com o objetivo de resolver os problemas de programação lineares e poder avaliar o desempenho das unidades vinícolas.

3.3 A caracterização da amostra

A base de dados é consolidada a partir de uma coleta de dados primários realizada para o projeto Observinho [15]. A coleta de dados [16] ocorreu nos seguintes municípios gaúchos: Bento Gonçalves, Caxias do Sul, Flores da Cunha, Garibaldi, Nova Pádua, São Marcos, Cotiporã, Antônio Prado, Farroupilha, Veranópolis, Monte Belo do Sul, Santa Maria e Santana do Livramento.

Como todos os elementos da população são conhecidos, recorre-se às técnicas da amostragem probabilística para a seleção da amostra. Esse tipo de amostragem implica em um sorteio com regras previamente determinadas. No presente caso, procedeu-se a seleção da amostra, obtida a partir das 660 empresas do setor, legalmente constituídas no período de análise, para o ano/safra 2008/2009, através da seguinte equação [17]:

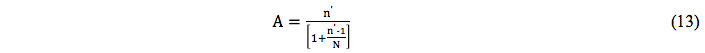
em que A é o tamanho da amostra selecionada; N é o tamanho da população; p são informações a priori sobre a característica da população [18]; sendo que n' é gerado através da equação:

em que z é o nível de 95% de confiança, o que resulta no valor crítico de 1,96; e é a probabilidade de erro que no presente caso é definida em 12%.

A partir das informações acima, a amostra ficou constituída por 59 vinícolas. O questionário foi elaborado em forma de planilha com perguntas relacionadas, por exemplo, ao capital amortizado, capacidade potencial de produção, produção efetiva da vinícola, custos fixos e variáveis e preço de venda.

3.4 O produto (output) e os fatores de produção (inputs) do setor vinícola

Existe uma grande variedade de categorias de vinho dentro da cadeia vinícola gaúcha, como apresentado anteriormente de acordo com as suas características básicas (físicas, químicas e organolépticas). No entanto, com o intuito de trabalhar com os dados mais agregados serão definidas apenas duas categorias de vinho conforme a classificação da Academia do Vinho, a saber: vinho de mesa ou comum (VM) - vinho elaborado a partir de variedades de uvas comuns (Concord, Herbemont, Isabel, Venus, Seyve Willard, Niágara, etc.), de espécies americanas (Vitis Labrusca, Vitis Rupestris, etc.); e vinho fino de mesa ou viníferas (VF) - o vinho fino é elaborado a partir de variedades de uvas nobres (Cabernet Sauvignon, Cabernet Franc, Pinot Noir, Merlot, Chardonnay, Riesling, Sauvignon Blanc, etc.) da espécie européia (Vitis vinifera).

A partir da divisão das unidades vinícolas em produtoras de VM ou VF, se tem o número de DMUs para cada modelo, ou seja, esta classificação possibilita avaliar o setor vinícola considerando as suas especificidades e a característica de produção de cada unidade de estudo. Deste modo, não incorre-se ao problema de avaliar empresas que produzem somente VF, o qual demonstra-se como um produto de valor agregado muito superior ao VM, com empresas que dedicam-se à produção de vinhos de "menor" qualidade.

Assim como produtos (outputs), no processo de avaliação da eficiência econômica das vinícolas, utiliza-se o volume produzido, em litros de vinho, de VF e VM, de cada empresa. Com a intenção de verificar a agregação de valor ao produto, utiliza-se como produto o faturamento das empresas, relacionando na análise a característica de cada empresa no seu processo produtivo (custo des produção) com a rentabilidade obtida pelas mesmas.

A partir da consolidação dos dados primários das vinícolas, os fatores de produção foram agrupados [19] em seis classes de insumos (inputs), conforme retratado na Tabela 1.

Tabela 1 - Agregação dos fatores de produção (insumos ou inputs)

Fonte: Elaborada pelos autores.

3.5 Caracterização da base de dados

Para avaliar os resultados obtidos, quanto à eficiência econômica das vinícolas, levando-se em consideração a realidade econômica do setor, é preciso conhecer o tamanho das mesmas. Esta classificação é derivada da oficialmente adotada no Brasil. No entanto, a realidade do setor exigiu que se adotasse uma classificação que fosse mais condizente com a sua dinâmica econômica, pois, as reconhecidas grandes vinícolas estariam fora da classificação oficial. Assim, resolveu-se adotar uma classificação que se julgou mais representativa, isto é, microempresa até R$ 2,4 milhões; pequena de R$ 2,4 milhões até R$ 10,5 milhões; a média de R$ 10,5 milhões até R$ 30 milhões e a grande acima de R$ 30 milhões (CAMPREGHER et al., 2013).

Assim, a partir das informações dispostas, a classificação das vinícolas amostrais (DMUs), quanto ao tamanho, evidência que a maioria das empresas amostradas, 72,88%, são consideradas micro vinícolas, dado que o valor de seu faturamento não atinge o montante de R$ 2.400.000,00, caracterizando a forte predominância de micro empresas no setor, visto que, entre as 59 vinícolas entrevistadas, 43 delas são micro vinícolas. Cabe destacar, ainda, que as vinícolas consideradas grandes e médias no espectro amostral, possuem participação individual de, aproximadamente, 5% (3 DMUs) na amostra. As pequenas vinícolas representam 16,95% (10 DMUs) no montante total de vinícolas analisadas.

Os levantamentos dos dados foram realizados tomando por base o ano/safra 2008/2009. Cabe ressaltar que afora as vinícolas mais estruturadas, as escriturações contábeis são realizadas em cadernetas de anotações. Isso constituiu em uma dificuldade a mais na coleta dos dados.

A fim de respeitar a idoneidade das unidades estudadas, vincula-se as 59 DMUs uma codificação que, nada mais é, do que a numeração sequencial para identificar cada empresa (DMU1, ..., DMU59). Ao analisar os dados, identificou-se 46 vinícolas produtoras de VM (destas, 5 empresas produzem apenas vinhos de mesa comum) e 54 produtoras de VF (sendo 13 delas produtoras apenas de vinhos viníferas), logo, 41 empresas produzem ambos os vinhos. Assim, a base de dados para os modelos DEA fica composta para o VM, com 46 DMUs, 6 insumos (inputs) e 2 produtos (outputs), e, para o VF, com 54 DMUs, 6 insumos (inputs) e 2 produtos (outputs), sendo tais variáveis identificadas na Tabela 2.

Tabela 2 - Identificação das variáveis utilizadas

Fonte: Elaborada pelos autores.

4. Resultados e discussões

Para verificar as eficiências individuais das DMUs e contornar um possível problema de confundir medidas de eficiência técnica (ET) com eficiência de escala (EEsc.), utiliza-se a Equação (5) e a Equação (7). Os resultados para o VM e VF apresentados nas Tabelas 3 e 4, respectivamente.

Tabela 3 - Resultados dos modelos DEA com retornos constantes e variáveis para o VM

    Fonte: Resultados da pesquisa.

Com base na Tabela 3, é possível verificar que para as 46 vinícolas (DMUs) produtoras de VM, 22 apresentam eficiência de escala (coeficiente de eficiência igual a 1), ou seja, 52,17% das empresas produtoras de VM estão operando com ineficiência de escala, e 47,83% em escala ótima. Analisando as unidades ineficientes, percebe-se que a ineficiência nas DMUs 1, 4, 7 e 12, é exclusivamente devido à escala incorreta, uma vez que sua medida de eficiência com retornos variáveis é máxima.

Tabela 4 - Resultados dos modelos DEA com retornos constantes e variáveis para o VF

 Fonte: Resultados da pesquisa.

A Tabela 4 apresenta os resultados quanto à eficiência de escala das DMUs produtoras de VF. Nesta é possível verificar que para as 54 vinícolas, 20 apresentam eficiência de escala, ou seja, 63% das empresas produtoras de VF estão operando com ineficiência de escala, e 37% em escala ótima. Analisando as unidades ineficientes, percebe-se que a ineficiência nas DMUs 1, 4, 6, 7, 22, 30, 41, 47, 50, 53 e 59, é exclusivamente devida à escala incorreta, uma vez que sua medida de eficiência com retornos variáveis é máxima.

Utilizando-se das informações a respeito dos preços dos insumos, após obter a eficiência técnica, calcula-se a eficiência econômica (EE), também conhecida como eficiência custo, das DMUs produtoras de VM e VF, e também a eficiência alocativa (EA). Dessa forma, com base no problema de minimização de custos (Equação 10), com retornos constantes a escala, obtém-se as quantidades ótimas de insumos que minimizam o custo de produção, permitindo determinar a EE (Equação 11) e a EA (Equação 12).

A Tabela 5 apresenta os resultados das medidas de EE, ET e EA para as DMUs produtoras de VM. Pode-se vislumbrar que as vinícolas produtoras de VM possuem um baixo nível de eficiência econômica, dado que apenas 6 DMUs são eficientes, com resultado igual a unidade, as demais 40 DMUs são ineficientes economicamente. Para a DMU1, por exemplo, o índice de eficiência econômica é igual a 0,74 indicando que esta possui uma ineficiência de 0,26. A medida de eficiência técnica para esta empresa é igual a 0,77, representando uma ineficiência técnica de 0,23, ou seja, existe a possibilidade de redução nos custos com insumo em, aproximadamente 23%, mantendo o mesmo nível de produção, para que esta possa operar com eficiência técnica. O índice de eficiência alocativa indica uma ineficiência de 0,04, sendo os insumos empregados de forma inadequada, em aproximadamente 4%.

Tabela 5 - Resultado do modelo de minimização de custos e medidas de eficiência VM

Fonte: Resultados da pesquisa.

A análise apresentada anteriormente pode ser realizada mecanicamente para cada DMU, mas para não tornar a leitura cansativa deixa-se a cargo do leitor essa tarefa.

Com o intuito de realizar uma análise agregada das DMUs, apresenta-se na Tabela 6, informações agregadas da Tabela 5. Nota-se que a medida de eficiência econômica média neste modelo é de 0,7241, representando uma ineficiência média de 0,2779, que indica, de outra forma, que as DMUs amostrais estão operando com 27,79% de ineficiência total. Neste sentido, das 46 empresas, 13,04% estão operando com eficiência econômica, ou seja, estas possuem eficiência técnica e alocativa.

Tabela 6 - Eficiência das DMUs produtoras de VM

Fonte: Resultados da pesquisa.

Seguindo estas definições, são identificadas 22 DMUs eficientes tecnicamente, equivalentes a 47,83% da amostra. A média da eficiência técnica é de 91,80%, representando uma ineficiência técnica de 8,2%, ou seja, existe a possibilidade de redução nos gastos com insumo em, aproximadamente 8%, mantendo o mesmo nível de produção. Por outro lado, o grupo das DMUs com ineficiência alocativa representa 84,78% da amostra, equivalente a 39 unidades produtoras (Tabela 6).

Logo, percebe-se que a ineficiência alocativa é um forte fator para as empresas vinícolas produtoras de VM estarem atuando de forma ineficiente economicamente (86,96%), ou seja, o emprego de insumos é feito em proporções inadequadas por estas empresas. Em outras palavras, as fontes de ineficiência técnica ocorrem devido ao uso excessivo de insumos, para dado nível de produção.

Observando mais detidamente a Tabela 5, um resultado interessante pode ser diagnosticado. As DMUs que possuem eficiência econômica são: DMU2, DMU3, DMU8, DMU23, DMU30 e DMU42. Cruzando estas informações com as informações de faturamento das mesmas, percebe-se que estas unidades são, respectivamente quanto ao tamanho, micro, pequena, pequena, micro, micro e micro. Desta forma, percebe-se que o grupo de empresas amostrais que operam com eficiência econômica, no ano safra em análise, é formado por micro e pequenas empresas, um resultado muito interessante do ponto de vista econômico, visto que, era de se esperar que as grandes empresas possuíssem uma relação de eficiência superior as pequenas. No entanto é preciso avaliar de maneira cuidadosa esse resultado, pois, ao se analisar a eficiência de escala das empresas, percebe-se que 50% das produtoras de VM, estavam operando com ineficiência de escala. Quando se analisa a eficiência alocativa há 39 DMUs produtoras de VM (aproximadamente 85% das DMUs amostradas), atuando com ineficiência alocativa. Sendo assim, ao se analisar as grandes e médias empresas percebe-se que na maioria das vezes o volume de produção dessas vinícolas está atrelado aos vinhos com menor agregação de valor, mas com a estrutura de custos de produção não muito distinto dos vinhos de maior agregação de valor. Isso proporciona um faturamento proporcionalmente menor para estas empresas, e a relação menos atraente do ponto de vista econômico entre insumos, volume produzido, e faturamento, se torna menos atraente vis-à-vis a empresas menores, que possuem estruturas de custos mais "enxutas" e com a utilização maciça da mão de obra familiar.

As medidas de eficiência (EE, ET e EA) para as DMUs produtoras de VF, são apresentadas na Tabela 7. Percebe-se que as empresas vinícolas de VF possuem baixo nível de eficiência econômica, pois, apenas 7 DMUs apresentam eficiência econômica (coeficiente máximo), sendo as outras 47 DMUs ineficientes economicamente. A interpretação mecânica para a DMU1 com um índice de eficiência econômica igual a 0,60, indica que esta possui uma ineficiência de 0,40. A medida de eficiência técnica para esta empresa é igual a 0,78, representando uma ineficiência técnica de 0,22. Ou seja, existe a possibilidade de redução nos gastos com insumo em, aproximadamente, 22%, mantendo o mesmo nível de produção, para que esta possa operar com eficiência técnica. O índice de eficiência alocativa aponta uma ineficiência de 0,76, sendo os insumos empregados, em cerca de 24%, de forma inadequada.

Tabela 7 - Resultado do modelo de minimização de custos e medidas de eficiência VF

Fonte: Resultados da pesquisa.

A Tabela 8 apresenta informações agregadas quanto a eficiência das DMUs produtoras de VF, sendo elaborada a partir dos resultados da Tabela 7. A partir dela, é possível constatar que a medida de eficiência econômica média apresentada pelas 54 DMUs analisadas é de 0,54, representando uma ineficiência média de 0,46, indicando que as DMUs amostrais estão operando com 46% de ineficiência total. Assim, das 54 empresas, apenas 12,96% estão operando com eficiência econômica, ou seja, estão operando com eficiência técnica e alocativa.

Tabela 8 - Eficiência das DMUs produtoras de VF

Fonte: Resultados da pesquisa.

Com base na Tabela 8, pode-se verificar que 20 DMUs das 54 analisadas, são eficiente tecnicamente, equivalente a 37,04% da amostra. A média da eficiência técnica é de, aproximadamente, 85%, representando uma ineficiência técnica de 15%. Nesse caso, existe a possibilidade de redução nos gastos com insumo, em média, de cerca de 15%, mantendo o mesmo nível de produção. O grupo das DMUs com ineficiência alocativa representa 85,19% da amostra, equivalente a 46 vinícolas. Sendo, portanto, apenas 8 DMUs (14,81%), eficiente alocativamente.

Assim, as empresas vinícolas produtoras de VF que atuam de forma ineficiente economicamente, ocorrem, principalmente, em ineficiência alocativa, devido a alocação dos seus insumos em proporções inadequadas, em relação aos seus respectivos preços. O uso excessivo de insumos, para dado nível de produção, causa ineficiência técnica. Isso ocorre em, aproximadamente, 63% das DMUs, causando ineficiência técnica.

As DMUs que possuem eficiência econômica na produção de VF são: DMU2, DMU8, DMU9, DMU26, DMU39, DMU40 e DMU45. Estas unidades são classificadas, respectivamente, quanto ao tamanho da empresa, em micro (DMU2, DMU9, DMU26, DMU39, DMU40 e DMU45) pequena (DMU8). Dentro das 54 vinícolas produtoras de VF, 7 operam de maneira eficiente economicamente, sendo 6 microempresas e 1 pequena empresa. Para efeito de análise, considera-se a discussão levantada anteriormente para as empresas produtoras de VM válida para as produtoras de VF. Assim, pode-se dizer que os custos produtivos envolvidos no processo de produção como um todo, principalmente custos administrativos, oneram relativamente em maior magnitude as médias e grandes empresas.

A hipótese de estudo de que as vinícolas analisadas operam de forma eficiente pode ser rejeitada, já que a maior parte das empresas estudadas, dado o resultado obtido através da DEA, possui ineficiência econômica, indicando um alto grau de ineficiência alocativa na produção de vinhos no Rio Grande do Sul. Porém, cabe destacar que a análise de eficiência econômica estudada aqui, é relativa, ou seja, as medidas encontradas são em relação às empresas amostradas. Isso indica que a partir das empresas que operam de maneira eficiente, ou de maior eficiência produtiva, é possível diagnosticar os elementos de custos que estão causando a ineficiência nas vinícolas.

5. Conclusão

Da amostra de vinícolas selecionadas (DMUs), pode-se verificar, no caso da eficiência de escala, que mais da metade das empresas produtoras de VM estão operando com ineficiência de escala, sendo a ineficiência causada exclusivamente devido à escala de produção incorreta. Para as DMUs produtoras de VF, o nível de ineficiência aumenta consideravelmente, ou seja, mais de 60% das empresas produtoras de VF estão operando com ineficiência de escala. Constatou-se também que, as empresas consideradas grandes, e também as consideradas médias, em virtude de seu faturamento, em sua totalidade estão operando com ineficiência de escala, devido a estarem utilizando uma escala incorreta, na produção de VF.

Ao analisar a eficiência econômica das vinícolas produtoras de VM, pode-se observar um baixo nível de eficiência econômica, estando cerca de 13% delas operando com eficiência econômica. Entretanto, a média da eficiência técnica das DMUs é de mais de 90%, mas ainda existe a possibilidade de redução nos gastos com insumo em, aproximadamente, 8%, mantendo o mesmo nível de produção, já que há ineficiência técnica. Por outro lado, o grupo das DMUs com ineficiência alocativa representou quase 85% da amostra.

As medidas de eficiência das DMUs produtoras de VF indicaram que cerca de 13% estão operando com eficiência econômica, ou seja, estão operando com eficiência técnica e alocativa, sendo que cerca de 37% são eficiente tecnicamente. O grupo das DMUs com ineficiência alocativa representou mais de 85% das vinícolas amostradas.

A ineficiência alocativa das vinícolas produtoras de VF decorrem, principalmente, da alocação de seus insumos em proporções inadequadas em relação aos seus respectivos preços. Enquanto que a ineficiência técnica, presente em mais de 60% das vinícolas se deveu ao uso excessivo de insumos para dado nível de produção.

Ao analisar a hipótese de estudo de que a maior parte das vinícolas estudadas operam de forma eficiente, percebe-se que esta hipótese não se confirma, dado que a maior parte das empresas avaliadas pelo modelo DEA apresentou resultado que indica ineficiência econômica e também ineficiência alocativa.

Um outro resultado alcançado é que há predomínio no grupo de vinícolas de VM e VF, ineficientes economicamente (coeficientes de eficiência menor do que a unidade), representando mais de 85% das empresas amostradas. Cabe destacar, ainda, que a EE média das empresas vinícolas produtoras de VM é maior do que a EE média das empresas produtoras de VF. Para finalizar, a análise de eficiência econômica estudada aqui é relativa, ou seja, as medidas encontradas são, em relação às empresas amostradas, o que indica que, a partir das empresas que operam de maneira eficiente, possuindo maior eficiência produtiva, é possível, também, que as empresas ineficientes, ao aperfeiçoarem as suas eficiências técnica e alocativa, passem a operar de forma mais eficiente em relação às economicamente eficientes.

Dada à representatividade da amostra de vinícolas analisadas no presente estudo, então os resultados aqui alcançados podem servir como uma boa aproximação da situação vivida pelas unidades vinícolas produtoras de vinho do Rio Grande do Sul, no ano-safra 2008/2009 em que ocorreu a coleta dos dados primários.

Contudo, apesar das limitações por parte da disponibilidade e dificuldade de se obter informações abrangendo o setor vinícola como um todo, fica o desafio de realizar um estudo complementar a este, envolvendo uma margem maior de vinícolas. Pode-se, também, aumentar a utilização de variáveis, insumos e produtos no modelo proposto para observar de maneira mais ampla o setor e as relações de produção. Outro fator que pode ser analisado é identificar os tipos de efeitos de escala individuais presentes no setor, visto que foi identificado um alto grau de ineficiência de escala no presente estudo. Assim, a consecução de estudos de acompanhamento das unidades produtivas possibilita obter resultados que são capazes de ampliar o entendimento do cenário econômico do SAI vitivinícola gaúcho.

Referências

ACADEMIA DO VINHO. Disponível em: <http://www.academiadovinho.com.br>. Acesso em: 2 mar. 2014.

ANGULO MEZA, L.; BIONDI NETO, L.; SOARES DE MELLO, J. C. C. B.; GOMES, E. G. (2005); "ISYDS - Integrated System for Decision Support (SIAD - Sistema Integrado de Apoio à Decisão): a software package for data envelopment analysis model". Pesquisa Operacional, v. 25, p. 493-503.

ASOGWA, B. C.; PENDA, S. T.; LAWAL, W. L. (2011); "Application of Data Envelopment Analysis to Evaluate Farm Resource Management of Nigerian Farmers". J Agri Sci, v. 2, p. 9-15.

BANKER, R. D.; CHARNES, H.; COOPER, W. W. (1984); "Some models for estimating technical and scale inefficiencies in data envelopment analysis". Management Science, v. 30, n. 9, p. 1078-1092.

BATALHA, M. O. (1997); Sistemas Agroindustriais: Definições e Correntes Metodológicas. In: BATALHA, M. O. (coord.). Gestão Agroindustrial, São Paulo: Atlas, v. 1, p. 23-48, 1997.

BOTTER, D. A.; PAULA, G. A.; LEITE, J. G.; CORDANI, L. K. (1996); Noções de estatística. São Paulo: IME/USP.

BOWLIN, W. F. (1998); "Measuring performance: an introduction to Data Envelopment Analysis (DEA)". The Journal of Cost Analysis & Management, Fall, p. 3-27.

CAMPREGHER, G. A., OLIVEIRA, G. N., FREITAS, C. A., HOECKEL, P. H. O. (2013); "Estimativas de custos das empresas produtoras de vinho e da renda agregada do arranjo vitivinícola gaúcho: uma primeira aproximação". Extensão Rural, v.20, p.86 - 131, Santa Maria.

CARLUCCI, F. V. (2012); Aplicação da Análise Envoltória de Dados (DEA) para avaliação do impacto das variáveis tamanho e localização na eficiência operacional de usinas de cana-de-açúcar na produção de açúcar e etanol no Brasil. 104 p. Dissertação (Mestrado em Administração de Organizações) – Faculdade de Economia, Administração e Contabilidade de Ribeirão Preto, Universidade de São Paulo, Ribeirão Preto, 2012. Disponível em: <http://www.teses.usp.br/teses/disponiveis/96/96132/tde-09112012-172303/pt-br.php>. Acesso em: 5 jun. 2013.

CHARNES, A.; COOPER, W. W.; LEWIN, A. Y.; SEIFORD, L. M. (1994); Data envelopment analysis: theory, methodology and applications. Boston: Kluwer Academic Publishers, 1994. Disponível em: <http://deazone.com/en/googlebook-orzz-kkc2mwc>. Acesso em: 4 abr. 2013.

CHARNES, A.; COOPER, W. W.; RHODES, E. (1978); "Measuring the efficiency of decision making units". European Journal of Operational Research, v.2, n.6, p. 429-444, 1978. Disponível em: <http://www.sciencedirect.com/science/article/pii/0377221778901388>. Acesso em: 4 abr. 2013.

COELLI, T.; RAO, D.S.P.; O'DONNELL, C. J.; BATTESE, G. E. (2005); An introduction to efficiency and productivity analysis. Second edition, Springer Science + Business Media, New York, United States of America.

DE KOEIJER, T. J.; WOSSINK, G. A. A.; STRUIK, P. C.; RENKEMA, J. A. (2002); "Measuring agricultural sustainability in terms of efficiency: the case of Dutch sugar beet growers". Journal of Environmental Management, v. 66, n. 1, p. 9-17.

FÄRE, R.; GROSSKOPF, S. (2000); Reference guide to OnFront. Sweden: Economic Measurement and Quality Corporation. 45p. Disponível em: <http://people.oregonstate.edu/~grosskos/ReferenceGuide.pdf>. Acesso em: 10 mar. 2013.

FARREL, M. J. (1957); "The measurement of productive efficiency". Journal Royal Statistical Society, v. 120, Part III, 253-290. Disponível em: <http://www.aae.wisc.edu/aae741/Ref/Farrell%201957.pdf>. Acesso em: 4 abr. 2013.

FERREIRA, M. A. M.; BRAGA, M. J. (2007); "Eficiência das Sociedades Cooperativas e de Capital na Indústria de Laticínios". RBE, Rio de Janeiro, v. 61, n. 2, p. 231-244, abr./jun.

FIGUEIREDO, S. P. (2005); Gestão do conhecimento, estratégias competitivas para a criação e mobilização do conhecimento na empresa. Rio de Janeiro: Qualitymark.

GOMES, A. P.; BAPTISTA, J. M. S. (2004); Análise envoltória de dados: conceitos e modelos básicos. In: SANTOS, M. L.; VIEIRA, W. C. Métodos quantitativos em economia. Viçosa: UFV, 2004.

GOMES, E. G.; MANGABEIRA, J. A. C. (2004); "Uso de Análise Envoltória de Dados em agricultura: O caso de Holambra". ENGEVISTA, v. 6, n. 1, p. 19-27, abril 2004.

GOMES, E. G.; SOARES DE MELLO, J. C. C. B.; BIONDI NETO, L. (2003); "Avaliação de eficiência por Análise de Envoltória de Dados: conceitos, aplicações à agricultura e integração com Sistemas de Informação Geográfica". Campinas: Embrapa Monitoramento por Satélite, 2003. 39p. (Documentos, 28). Disponível em: <http://www.cnpm.embrapa.br/publica/download/d28_envoltdados_vf.pdf>. Acesso em: 2 jun. 2013.

GOMES, E. G.; SOARES DE MELLO, J. C. C. B.; SERAPIÃO, B. P.; LINS, M. P. E.; BIONDI, L. N. (2001); Avaliação de eficiência de companhias aéreas brasileiras: uma abordagem por Análise Envoltória de Dados. In: SETTI, J. R. A.; LIMA JÚNIOR, O. F. (eds.). Panorama Nacional da Pesquisa em Transportes 2001, v. 2, 2001, p. 125-133.

IBRAVIN (Instituto Brasileiro do Vinho). Disponível em: <http://www.ibravin.org.br/>. Acesso em: 4 nov. 2013.

KRASACHAT, W. (2002); "Deforestation and productivity growth in Thai agriculture". In: International Symppsium on Sustainable Food Security and managing Natural Resources in Southeast Asia: Challenges for the 21st Century, 2002, Chiang Mai. Annals..., 2002.

LANSINK, A. O.; PIETOLA, K.; BÄCKMAN, S. (2002); "Efficiency and productivity of conventional and organic farms in Finland 1994-1997". European Review of Agricultural Economics, v. 29, n. 1, p. 51-65.

MAGALHÃES, K. A.; CAMPOS, R. T. (2006); "Eficiência técnica e desempenho econômico de produtores de leite no estado do Ceará, Brasil". RER, Rio de Janeiro, vol. 44, n. 4, p. 695-711, out./dez. 2006.

MAS-COLELL, A.; WHINSTON, M. D.; GREEN, J. R. (1995); Microeconomic theory. New York: Oxford University Press.

MONCHUK, D. C.; CHEN, Z. (2008); "Explaining Production Inefficiency in China's Agriculture using Data Envelope Analysis and Semi-Parametric Bootstrapping". The American Agricultural Economics Association Annual Meetings. Orlando, Florida, June 27-29.

OIV (Organização Internacional da Vinha e do Vinho). Disponível em <http://www.oiv.int/oiv/cms/index>. Acesso em: 1 jul. 2013.

PEREIRA, C. N. (2012); Análise exploratória da eficiência produtiva das usinas de cana-de-açúcar na região Centro-Sul do Brasil com o método Análise Envoltória de Dados (DEA) – Índice de Malmquist. 2012. Dissertação de Mestrado (Mestrado em Desenvolvimento econômico), Instituto de Economia, Universidade Estadual de Campinas, Campinas, SP, 2012.

ROLOFF, M; CAUS, M. (2014); (Ed.) Avaliação setorial 2013. IBRAVIN, 2014. Disponível em: <http://www.ibravin.org.br/public/upload/statistics/1380742265.pdf >. Acesso em: 7 fev. 2014.

SEIFORD, L. M.; ZHU, J. (1999); "An Investigation of returns to scale in data envelopment analysis". Omega - The Journal of Management Science, v. 29, n. 3, p. 255-265.

SOARES DE MELLO, J. C. C. B.; MEZA, L. A.; GOMES, E. G.; BIONDI NETO, L. (2005); Curso de Análise de Envoltória de Dados. In: XXXVII Simpósio Brasileiro de Pesquisa Operacional, Gramado, 2005. Anais... Disponível em: <http://www.uff.br/decisao/sbpo2005_curso.pdf>. Acesso em: 13 mai. 2013.

THOMPSON, A. A. Jr.; FORMBY, J. P. (2003); Microeconomia da firma: teoria e prática. Rio de Janeiro: LTC – Livros Técnicos e Científicos Editora S.A.

UVIBRA (União Brasileira de Vitivinicultura). Disponível em <http://www.uvibra.com.br>. Acesso em: 6 jul. 2013.

VICENTE, J. R. (2012); "Produtividade total de fatores e eficiência no setor de lavouras da agricultura brasileira". Revista de Economia e Agronegócio, vol. 9, n. 3.

VILELA, D. L.; NAGANO, M. S.; MERLO, E. M. (2007); "Aplicação da Análise Envoltória de Dados em Cooperativas de Crédito Rural". RAC, 2ª Edição Especial, p. 99-120.

ZOFIO, J. L.; LOVELL, C. A. K. (2001); "Graph efficiency and productivity measures: an application to U.S. agriculture". Applied Economics, v. 33, n. 11, p. 1433-1442.

1. Doutorando do Programa de Pós-Graduação em Economia do Desenvolvimento da PUCRS (PPGE/PUCRS). Mestre em Economia e Desenvolvimento (PPGE&D/UFSM). E-mail: ph.hoeckel@gmail.com

2. Pós-Doutor em Estatística e Experimentação Agropecuária (UFLA). Doutor em Economia Aplicada (ESALQ/USP), Professor Associado da UFSM e do Programa de Pós-Graduação em Economia e Desenvolvimento (PPGE&D). E-mail: lcv589@gmail.com

3. Tais regiões são: Campanha, Serra do Sudeste, Serra Gaúcha e Campos de Cima da Serra, no Rio Grande do Sul; Planalto Catarinense, em Santa Catarina; e Vale do São Francisco em Pernambuco. Para mais informações ver Roloff e Caus (2014). Disponível em: <http://www.ibravin.org.br/public/upload/statistics/1380742265.pdf>. Acesso em: 7 fev. 2014.

4. Disponível em: <http://www.academiadovinho.com.br>. Acesso em: 2 mar. 2013.

5. Segundo o IBRAVIN (2013) o Rio Grande do Sul sedia as principais vinícolas brasileiras, tendo, atualmente, 731 vinícolas legalmente cadastradas.

6. Segundo dados da OIV, disponíveis em: <http://www.oiv.int/oiv/cms/index>. Acesso em: 1 jul. 2013.

7. Termo em inglês, Data Envelopment Analysis.

8. Da mesma forma, Coelli et al. (2005) afirmam que a eficiência alocativa e técnica se combinam para proporcionar uma medida geral da eficiência econômica.

9. Termo em inglês, Decision Making Units.

10.A DEA apresenta algumas limitações de uso, as quais estão descritas em Gomes e Baptista (2004).

11.Entre as vantagens estão, segundo Gomes e Baptista (2004), a possibilidade de decompor a eficiência econômica em técnica e alocativa, além dos efeitos de escala. A DEA permite, ainda, encontrar quais foram as DMUs eficientes que foram as responsáveis por determinada DMU ter sido considerada ineficiente, indicando em quais variáveis devem ser feitas alterações.

12. A metodologia apresentada como base nesta subseção é adaptada de Charnes, Cooper e Rhodes (1978).

13.O sistema produtivo da vitivinicultura segue a definição de Sistema Agroindustrial (SAI) proposta por Batalha (1997), ou seja, trata-se de um conjunto de atividades que concorrem para a produção de mercadorias de origem agroindustriais, desde a produção dos insumos até a chegada do produto final ao consumidor.

14. Disponível em: http://www.uff.br/decisao. Acesso em: 2 set. 2013. Para mais informações ver Angulo Meza et al. (2005).

15. Observinho - Projeto de implantação de um Observatório do Vinho na Serra Gaúcha: Realização de pesquisas, seminários e reuniões para a constituição de um Observatório que colete e produza informações relevantes para o fortalecimento do APL Vitivinícola da Serra Gaúcha. As informações sobre os custos produtivos do setor vinícola foram coletados por pesquisadores participantes do projeto Observinho, sendo este financiado pelo CNPq e apoiado pelo IBRAVIN, com o objetivo de mensurar os custos de produção do vinho no Rio Grande do Sul.

16. Da qual os autores do presente estudo fizeram parte, e detém autorização dos responsáveis pelo projeto para a reprodução deste estudo utilizando a base de dados da referida pesquisa.

17. Essa fórmula é representada em Botter et al. (1996).

18.Representa a porcentagem com que determinado fenômeno se verifica, como as informação a priori não estavam disponíveis acerca do valor de p, é recomendável que se utilize p = 0,5.

19. Os fatores de produção foram agrupados em variáveis constituídas pelo custo de produção em R$.