Espacios. Vol. 36 (Nº 23) Año 2015. Pág. 21

Framework Computacional para a programação da produção de gabaritos de montagem com restrição de adjacência

Computational Framework for programming the production assembly jigs with restriction adjacency

Valdecir de Oliveira PEREIRA 1; André Felipe Henriques LIBRANTZ 2

Recibido: 15/08/15 • Aprobado: 27/10/2015

Contenido

1. Introdução

2. Fundamentação teórica

3. Metodologia de pesquisa

4. Exemplos de aplicação do framework Proposto

5. Resultados e discussões

6. Conclusões

Referências bibliográficas

1. Introdução

A concorrência mundial tem pressionado as empresas a cada dia produzirem mais, em menos tempo, com menor custo, com melhor qualidade, respeitando o meio ambiente e com grande variedade de produtos, tendendo a produtos personalizados. A cada dia a pressão por sistemas produtivos que sejam mais eficientes e controláveis estimula a pesquisa por alternativas inteligentes e viáveis.

Dentro deste cenário, a programação da produção é objeto de pesquisa no mundo nas últimas décadas, sempre buscando soluções ótimas, ou boas, do ponto de vista de redução de tempo e custo de setup, makespan, tempo de fluxo, atraso das tarefas e no atendimento das ordens de produção dentro de prazos de entrega e com a melhor utilização dos recursos da fábrica (Morais, 2009; Tubino, 2009). Dentre os diversos tipos de indústria existem sempre novos desafios que partem das características do processo de fabricação, da forma de atendimento das ordens às restrições técnicas e tecnológicas (Duin, Sluis, 2006). Gerar uma programação das ordens de produção considerando todas estas características e garantir bons resultados em tempo computacional aceitável é um grande desafio e gera espaço para novas pesquisas (Hvolby, 2010; Xing, 2009)

Turatti (2009) sugere que o sistema de programação de produção deve reproduzir as decisões estratégicas da empresa, com regras de programação que respeitem estas decisões, tornando-o assim um sistema que busca os melhores resultados em uso da capacidade fabril, direcionando os esforços da fábrica em busca dos objetivos estratégicos da empresa.

Framinan e Ruiz (2010) realizaram um levantamento em 184 artigos sobre programação de produção. Dentre todos artigos, menos de 3% consideravam condições realistas de produção.

Outro fato que aponta a preocupação em obter em soluções de programação da produção, foi a pesquisa realizada por (Giacon,2011), apoiada pela FIESP (Federação das Indústrias do Estado de São Paulo), que destacou que apenas 11% dos respondentes utilizam sistemas de programação da produção e 40% dos respondentes MTO (Make to order) disseram que pretendem investir neste tipo de solução. Esta mesma pesquisa demonstra que a adoção de soluções ERP (Enterprise Resource Planning) já é bastante difundida no mercado brasileiro e com instalações sendo utilizadas há mais de 10 anos.

A adoção de soluções de ERP, que normalmente utilizam algoritmos MRP I (Material Requirements Planning) ou MRP II (Manufacturing Resource Planning), não são capazes de gerar uma programação detalhada para a fábrica com eficiência. A deficiência na geração de uma programação detalhada ocorre em função de diversas características como: lead times superestimados, programação infinita, mesmo com a adoção do módulo CRP (Capacity Requirements Planning) que faz uma verificação aproximada da capacidade e não detalhada como nas soluções de programação da produção (Girotti,2011).

Outros trabalhos descrevem as vantagens das soluções de programação da produção também conhecidas pelo nome comercial APS (Advanced Planning and Scheduling) em relação às técnicas MRP I e II, como a flexibilidade para a geração de cenários sendo uma ferramenta de apoio à tomada de decisão, que não é possível em soluções ERP (Girotti,2011).

Dentre as diversas técnicas possíveis para o desenvolvimento de soluções APS, este trabalho apresenta um framework computacional, utilizando um diagrama de classes em UML(Unified Modeling Language) e a aplicação do método de busca CSP (Constraint Satisfaction Problem), como método de busca local, associado a regras de liberação e Algoritmos Genéticos, concluindo com o desenvolvimento de software protótipo.

O restante deste artigo está organizado como segue: na seção dois são apresentados os principais fundamentos teóricos. A metodologia é apresentada na seção 2. Na terceira seção são apresentados e discutidos os resultados obtidos. Na quarta e última seção são apresentadas as conclusões bem como sugestões de trabalhos futuros.

2. Fundamentação teórica

2.1. Framework conceitual

O framework conceitual é o resultado do processo qualitativo de teorização e pode ser compreendido como uma rede de conceitos que juntos oferecem a compreensão abrangente de um fenômeno. Em outras palavras pode ser entendido como uma rede de conceitos organizados para representar entidades do mundo real. O frequente uso do termo framework no Desenvolvimento de software segue os princípios de orientação a objetos. Hautamäki (2005) propôs como definição para framework um esqueleto de implementação de uma aplicação ou de um subsistema em um domínio de problema em particular. É composto por classes concretas ou abstratas e define um modelo de interação ou colaboração entre as instâncias de classes definidas pelo framework. Diferente de uma biblioteca de classes onde a relação entre as classes fica a cargo da aplicação, em um framework já está definido o papel de relações entre as classes. Por outro lado, os frameworks são mais dependentes do domínio do problema (Taligent, 1994).

Framework oferece infraestrutura de projeto permitindo ao desenvolvedor reduzir o esforço. As interconexões estabelecidas definem a arquitetura da aplicação. O desenvolvedor faz uso do framework estendendo e moldando as suas necessidades específicas (Dias, 2004). Nas próximas seções serão apresentadas todas as entidades do framework proposto, métodos de escolha, restrições, métodos de sequenciamento e relacionamento entre entidades.

2.2. Algoritmos de busca e otimização

2.2.1. CSP (Constraint Satisfaction Problem)

O CSP (Constraint Satisfaction Problem) é um sistema de busca onde se conhece os estados possíveis com um conjunto de variáveis sob um determinado domínio (Russel; Norvig, 2010). O CSP (Constraint Satisfaction Problem) pode ser considerado como o estudo de sistemas computacionais baseados em restrições, tendo por fundamento resolver problemas apenas especificando os requisitos (restrições) sobre a área problema ou, em outras palavras, sobre os valores possíveis (domínio) das variáveis. A solução para o problema, portanto, um conjunto de valores que atendam todos os requisitos (Pereira, 2011).

CSP (Constraint Satisfaction Problem) também pode ser modelado por meio de grafo de restrições, formando uma rede onde as variáveis de decisão são representadas pelos vértices e as restrições pelas arestas, que permite a utilização das ferramentas para manipulação de grafos. Dentre as principais formas de busca em restrições modeladas através de grafos podemos citar: consistência de nó, consistência de arco e consistência de caminho. Todos com o mesmo objetivo de minimizar o retrocesso do algoritmo por não ter encontrado a solução pelo caminho selecionado inicialmente (Brucker, 2002)

Também pode ser encontrada na literatura alternativa para resolução de problemas de satisfação de restrições como o particionamento do problema, denominado DCSP (Distributed Constraint Satisfaction Problem), cujo principal objetivo é permitir o processamento em paralelo e distribuído das restrições e com a possibilidade do uso de agentes inteligentes (Pereira, 2006; Giacomet, 2010).

Outra característica importante é a facilidade em modelar o problema, uma vez que se podem adicionar restrições independentemente de como será a solução do problema. Também difere de outros tipos de busca, por que não interessa qual o caminho para encontrar a solução, mas se encontrou uma solução que satisfaça as restrições (Russel;Norvig, 2010).

Problemas reais também foram observados no trabalho de (Framinan, Ruiz, 2010) com o uso de CSP (Constraint Satisfaction Problem). Zeballon (2010) descreveu em seu trabalho a aplicação do uso de restrições para a programação de produção. Além do detalhamento dos tipos de restrições o autor argumenta sobre a facilidade de modelar problemas reais, pois durante o desenvolvimento do modelo não é necessário ter a preocupação com qual tipo de solução.

2.2.2. Algoritmos Genéticos

A técnica de Algoritmos Genéticos consiste em um método de busca e otimização, baseado no princípio da seleção e evolução das espécies proposto por Charles Darwin. O algoritmo proposto por Holland na década de 70 utilizou de forma análoga os conceitos da biologia, como a sobrevivência dos mais aptos e a troca de informações de forma estruturada. Holland definiu como representação do indivíduo um conjunto de alelos representados por uma sequência de números zeros e uns, conforme pode ser observado na figura 1.

Figura 1 - Representação de um indivíduo.

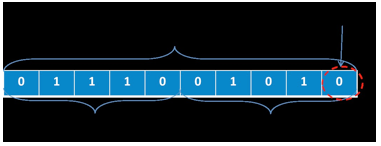
Fonte: Rosa (2011).

A população inicial de indivíduos é na maioria das vezes gerada de forma aleatória. No entanto, existem situações que pode ser mais vantajoso utilizar como população inicial outros métodos, como por exemplo, o resultado de uma busca heurística. Os indivíduos são avaliados por uma função chamada fitness na qual o indivíduo mais apto tem os melhores valores (função objetivo), seja de maximização ou minimização. Sobre a população são aplicados dois operadores, cruzamento (Crossover) e mutação (Mutation).  Após a aplicação dos operadores é realizada novamente a função fitness, onde será selecionada apenas uma parte de toda a população restante para a nova geração. Desta forma a cada geração deve haver uma população (soluções) mais próxima do objetivo ou das melhores soluções. O algoritmo pode parar quando atingir um número de gerações, duração de tempo em processamento ou ter atingido um determinado objetivo (Araújo et al., 2007).

Figura 2 . Esquema de funcionamento do Algoritmo Genético.

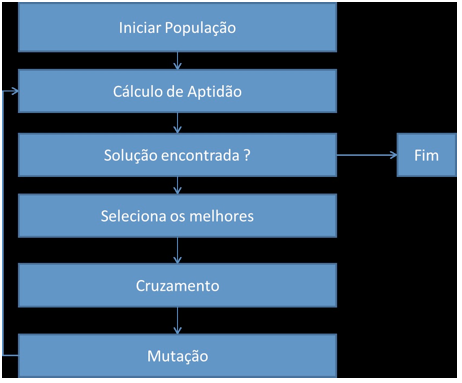
Fonte: Araújo et al. (2007).

Foram utilizadas como parâmetros para o algoritmo genético para o exemplo 1 população inicial de 8 indivíduos, 10 gerações, taxa de mutação de 4%. Para o exemplo 2 e exemplo 3 uma população inicial de 20 indivíduos, 30 gerações, taxa de mutação 4%. Em todos os casos o método de cruzamento foi o PMX (Partially Matched Crossover) e o método de mutação RSM (Reverse Sequence Mutation)(Abdoun, Abouchabacka, 2011).

2.3. Entidades

A capacidade produtiva da empresa pode ser representada pela disponibilidade de recursos produtivos (máquinas, operadores, ferramentas, materiais, energia, etc.), no framework será denominado de recursos, que podem ser divididos em recursos discretos e recursos contínuos, sendo que cada um representa melhor algum tipo de recurso (Weglaz et al.., 2010). O recurso discreto (RRD) representa normalmente postos de trabalho e máquinas e pode ser entendido que sua disponibilidade é a variação da eficiência em função do tempo, ou seja, conforme muda o período, poderá ou não estar disponível com eficiência diferente. Por exemplo: suponha uma empresa que possui seus recursos disponíveis a uma eficiência produtiva de 100% durante o horário das 8h00min as 12h00min, indisponível das 12h00min as 13h00min, em função do horário de almoço, ou seja eficiência de 0%, retomando das 13h00min as 17h00min a eficiência de 100%. Mas somente de segunda a sexta feira, exceto feriados. Podemos concluir que os recursos discretos tem sua disponibilidade somente das 8h00min as 12h00min e das 13h00min as 17h00min, ou seja 8 horas por dia, conforme pode ser observado na Figura 3 .Outra informação é que poderia executar múltiplas operações simultaneamente. Para restringir apenas uma operação durante determinado período, deverá ser adiconada nova restrição ROA ( operação alocada), que é tratada no decorrer deste artigo.

Figura 3 - Exemplo de variação de eficiência em recursos discretos

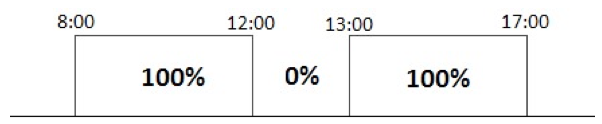
Nos recursos contínuos que podem representar volume, como consumo de energia, utilização de funcionários, entre outros, a disponibilidade varia em função dos limites inferior e superior, em função do tempo. Quando uma operação ou um recurso, adicionar (adiciona), por exemplo, dois funcionários, caso uma segunda operação necessite também de dois funcionários deverá esperar o término da operação e a respectiva devolução (reduzir) dos funcionários. O modo como são utilizados os recursos contínuos podem ser observados na Tabela 1.

Tabela 1 – Formas de consumo dos recursos contínuos.

Fonte: Adaptado de Weglaz et al ( 2010).

As operações serão nomeadas a partir deste ponto simplesmente como OP e as ordens de produção que são representadas no framework como um conjunto de operações passará a ser nomeadas como ORD.

2.4.  Métodos de Escolha

As restrições que utilizam recursos RRD e RRC, que serão detalhadas adiante, possuem um método de escolha para quando possuírem mais de um recurso capaz de executar a mesma operação, a escolha de qual será o recurso eleito depende do método escolhido, os quais seguem:

a) Disponível primeiro: Dentre todos os recursos definidos na restrição o que estiver disponível para executar a operação o mais breve possível, será o recurso eleito.

b) Terminar primeiro: Dentre todos os recursos definidos na restrição o que terminar a operação o mais breve possível, será o recurso eleito.

c) Menor Custo: Dentre todos os recursos definidos na restrição, independente do início ou término da operação, o que consumir menos recursos financeiros será o recurso eleito.

d) Menor Tempo de Processamento: Dentre todos os recursos definidos na restrição, o recurso em que a duração total da operação for menor, será o recurso eleito.

2.5. Restrições

As restrições são entidades que limitam, condicionam ou impedem a execução de uma operação. Devemos estudar todas as restrições para que durante o processo de modelagem possamos utilizar as que melhor representarem as características do processo, ressaltando que as restrições somente podem ser associadas a operações e recursos. Seguem abaixo a relação de restrições utilizadas neste trabalho com suas respectivas características:

a) RRD (Recurso Discreto): Esta restrição valida um conjunto de recursos discretos utilizando um método de escolha conforme citado anteriormente, retornando apenas um recurso válido para a restrição. Caso sejam necessários dois recursos simultâneos para a mesma operação, deve-se adicionar outra restrição deste tipo.

b) RRC (Recurso Contínuo): Na restrição de recurso contínuo, devemos além do método de escolha do recurso, que é o mesmo utilizado em recursos discretos, informar quais recursos irão participar do processo de escolha, pois somente um recurso válido contínuo será definido por restrição. Caso deseje mais de um recurso válido contínuo definido, deverá adicionar mais uma restrição com os respectivos recursos contínuos. Para adicionar um recurso contínuo será necessário informar uma quantidade e o método de uso conforme apresentado na Tabela 1.

c) RDP (Dependência entre operações): Para que a operação com esta restrição seja alocada a operação antecessora deverá estar devidamente alocada.

d) ROA (Operação Alocada): Esta restrição garante que apenas será alocada a operação com esta restrição se não existir nenhuma operação alocada neste recurso e adjacentes no mesmo período.

2.6. Métodos de Sequenciamento

Os métodos de sequenciamento podem ser aplicados em ordens e operações, dependendo das regras de programação, utilizam um ou outro, ou até mesmo ambos de forma combinada. No método de sequenciamento para frente verifica se todas as restrições podem ser atendidas o mais breve possível, caso exista alguma que não atenda, utiliza-se o início mais tarde da restrição que violou, mas que esteja disponível, então se verifica novamente com todas as restrições, até que todas sejam atendidas ao mesmo tempo ou ultrapasse o horizonte de programação, onde será considerada como uma programação fora da área de busca. No método de sequenciamento para trás, uma operação valida todas suas restrições o mais tarde possível(data de entrega), caso alguma restrição seja violada, utiliza-se o término mais cedo da restrição que violou, então verifica se novamente todas as restrições até que todas sejam atendidas no mesmo término, ou o agora seja ultrapassado, onde será considerada como uma programação fora da área de busca.  (Horny-Chyi, 2006)

2.7.  Método de Programação/Sequenciamento

As regras de sequenciamento também conhecidas como regras de despacho determinam qual o critério de escolha das ordens ou operações que vão disputar os recursos da fábrica. As regras de sequenciamento seguem normalmente as políticas de atendimento das ordens definidas pela empresa, ressaltando que podem ser utilizadas diversas regras de sequenciamento sobre um mesmo ambiente a fim de se obter a melhor programação para a empresa naquele momento. Nesse artigo, foram utilizadas as regras de despacho SPT (shortest process-time), cujo objetivo principal é programar primeiro as operações com o menor tempo de processamento por meio dos métodos de programação "para frente" de cada operação individualmente mantendo programada a operação que tiver menor duração. Como segundo método de programação foram utilizados os Algoritmos genéticos (AG), no qual os cromossomos que representam operações são sequenciados uma após outro utilizando o método de programação para frente.

3. Metodologia de pesquisa

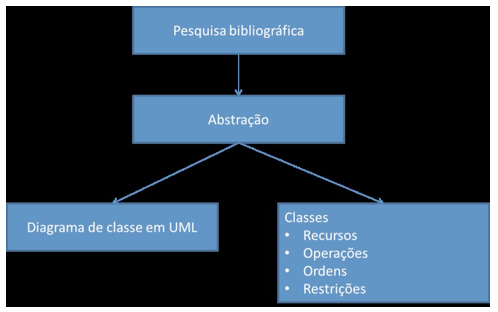
Este trabalho caracteriza-se como pesquisa de natureza aplicada para gerar conhecimento, a partir da aplicação da solução em problemas específicos. De acordo com Gil (2002), este trabalho pode ser classificado como exploratório-descritivo. Classifica-se como exploratório, pois visa proporcionar maior familiaridade com o objeto em estudo, tornando-o explícito através da apresentação do framework e algoritmos correlatos, descritiva, pois detalha as atividades de modelagem de sistemas produtivos através de um exemplo de modelagem e um estudo de caso. Teve início com uma pesquisa bibliográfica realizada, principalmente por meio de sistemas de busca no portal de periódicos da CAPES, Science Direct, Scielo, EBSCO host,  além de livros de administração de produção (Figura 4).

Figura 4 . Metodologia de pesquisa

Fonte: o autor.

O diagrama de classes foi desenvolvido utilizando a notação UML (Unified Modeling Language) e as premissas de abstração em modelagem de sistemas baseados em orientação a objetos. A figura 5 apresenta o diagrama de classes do framework proposto.

Figura 5 - Diagrama de Classes do Framework proposto.

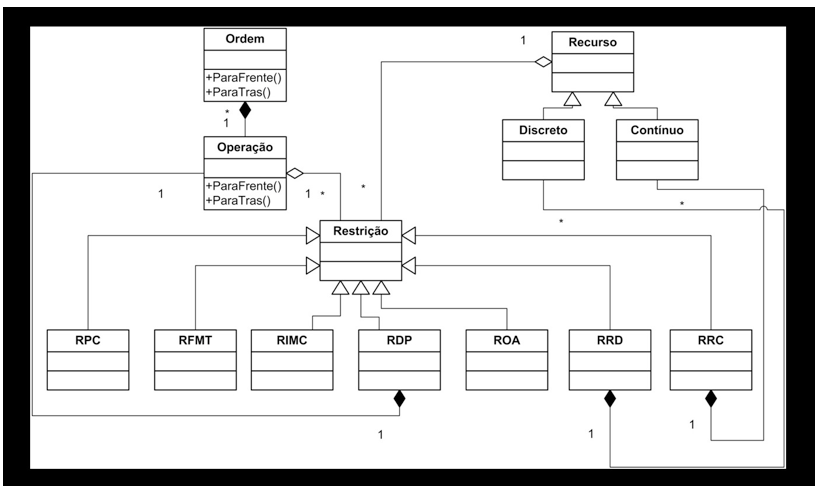
Fonte: O autor.

Esse diagrama em UML representa a agregação de restrições em recursos ou operações.  As restrições são especializadas em diversos tipos, sendo que cada tipo de restrição tem seu próprio objetivo, e as restrições RRC e RRD são compostas por um ou mais recursos dependendo da necessidade. Os recursos são especializados em discretos e contínuos e as ordens compostas por um conjunto de operações. Neste contexto, podem-se criar novos tipos de restrição caso sejam necessários e sua agregação também ocorre de forma dinâmica, o que facilita a modelagem de problemas a partir de componentes razoavelmente simples. 

4. Exemplos de aplicação do framework Proposto

O framework proposto foi utilizado no desenvolvimento de um software protótipo em linguagem Delphi e possui os seguintes módulos: Cadastro de Recursos, Cadastro de Turnos, Cadastro de Produtos/Roteiros, Cadastro de Ordens, Estados de calendário, Tela de Programação. O software foi aplicado em problemas de programação da produção de gabaritos de montagens na indústria aeronáutica reportado na literatura e os resultados foram comparados com os valores ótimos já conhecidos (Silva et al., 2011). Na Figura 4 pode-se observar a tela destinada ao sequenciamento das operações. Como exemplo, já se tem uma ordem com sua respectiva sequência de operações em função do tempo alocado no gráfico de Gantt (Pereira, Librantz, 2013).

Figura 6. Tela do Gráfico de Gantt com todas as ordens programadas.

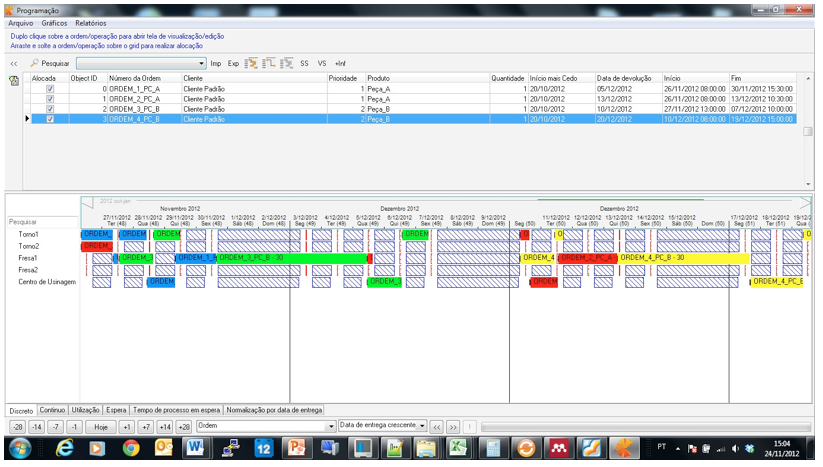
Fonte: o autor

Além do sequenciamento manual com o uso do mouse, o software possibilita a utilização de duas técnicas distintas para o sequenciamento das ordens de produção, sendo a primeira baseada em regras de liberação e a segunda com a utilização de algoritmos genéticos, ambas utilizadas nos exemplos a seguir.

4.1 Exemplo 1

Com os  dados publicados por Morabito (2011) foi possivel reconstruir o mesmo ambiente agora estruturado com o framework proposto. Desta forma foram criados seis recursos discretos, sendo três gabaritos com restrição ROA, que garante que não serão programadas mais de uma operação simultaneamente neste recurso e recursos adjacentes, ou seja, somente será alocada se o rescurso que possui a restrição e adjacentes não tenham operações em execução. Foi adicionado também um recurso contínuo a fim de representar o numero de funcionários nescessários para a execução das operações conforme pode ser observado na Tabela 2 . Para o problema também foram criadas três ordens de produção com quatro operações cada numeradas de dez em dez confome Tabela 3 . Os turnos de trabalho foram definidos para recuros discretos como disponivel a 100% de eficiencia durante 24 horas por dia. O turno de trabalho do recurso contínuo foi definido como mínimo 0 e maximo 4, pois  nosso objetivo não é restringir neste momento o numero de funcionários, mas apenas analisar a necessidade em função do tempo.

Tabela 2 – Exemplo de recursos disponíveis na empresa em estudo.

Fonte: Adaptado de Silva et al ( 2011).

-----

Tabela 3. Operações utilizadas no exemplo1.

Fonte: Adaptado de Silva et al ( 2011).

4.2 Exemplo 2

O segundo exemplo é baseado em uma aplicação prática e foi adicionada ao trabalho a fim de termos um problema com  mais recursos e que posteriormente sejam adicionadas novas restrições, conforme listado na tabela 3. Os recursos são similares a Tabela 2 mas foram adicionados novos postos e novas bancadas totalizando oito em cada e mais um recurso contínuo intitulado" Funcionários", que possui a mesma função do exemplo anterior.

Tabela 3. Recursos utilizados no exemplo 2.

Na tabela 4 são apresentadas as ordens de operação utilizadas no exemplo 2.

Tabela 4. Operações utilizadas no exemplo 2.

Fonte:  Adaptado de Silva et al (2011).

5. Resultados e discussões

Para os exemplos 1 e 2 foram testadas duas técnicas distintas de programação, a regra de liberação SPT (shortest process-time) e os Algoritmos Genéticos (AG). Cabe ressaltar que  o método de programação CSP (Constraint Satisfaction Problem) foi utilizado em uma busca local para resolver as restrições com os dois métodos conforme citado nas seções anteriores, para frente e a para trás. Nos exemplos somente foram utilizados os métodos de programação para frente, sendo que o método SPT (shortest process-time), faz a ordenação das operações pelo tempo de processamento, enquanto o algoritmo genético utiliza a sequência gerada nos cromossomos, sequenciando-os utilizando os métodos de programação para frente

No caso do exemplo 1,  ambas as técnicas SPT(shortest  process-time) e de algoritmos genéticos  convergiram rapidamente para a solução ótima ( makespan de 41 horas). A Figura 7 apresenta a tela do software desenvolvido para validar o framework proposto com a alocação das operações da Tabela 3. A Figura 8 apresenta parte da tela do software, representando a nescessidade de funcionários para a execução das operações da Tabela 3. Nesse caso, o Lead time acumulado, ou seja a soma do lead time de todas as ordens no sistema para todas as soluções ótimas com algoritmo genético foi de 103 horas.

Figura 7. Tela do software desenvolvido utilizando o framework proposto.

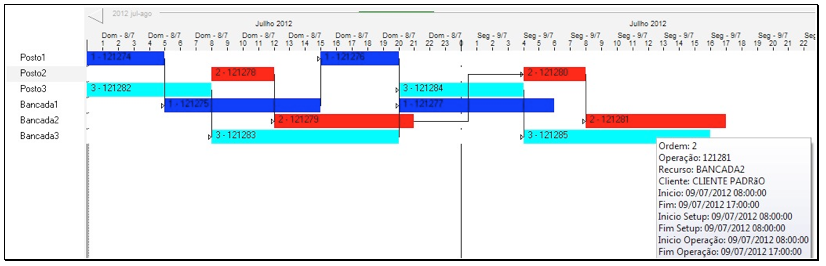
Figura 8. Representação da necessidade do recurso Funcionários.

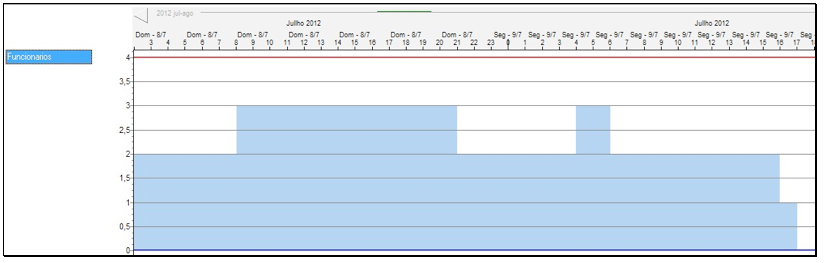
Fonte: O autor.

No exemplo 2 também foram aplicadas a regra de despacho SPT(shortest  process-time) e os algoritmos genéticos (AG). Com a primeira técnica foi obtido um makespan de 1040 horas, sendo que a solução ótima para makespan de 975 horas, ou seja, não se alcançou a solução ótima para este problema com o uso desta regra. Além disso o Leadtime acumulado das ordens foi de 9895 horas. No caso da aplicaçãp dos AG foram obtidas 20 soluções ótimas para o problema, ou seja, para o mesmo makespan de 975 ( ótimo). Pode se observar na Figura 9 que o lead time acumulado em cada solução gerada pelo algoritimo genético muda significativamente entre 10950 a 10360 horas (uma variação de 605 horas), ou seja, no problema estudado com o mesmo makespan  temos diversas soluções possíves que pode levar a análise de outros critérios como o leadtime total, que quando aumentado representa mais material em processo possivelmente entre operações, levando ao aumento do WIP(Work in process) .

Figura 9.  Lead Time acumulado.

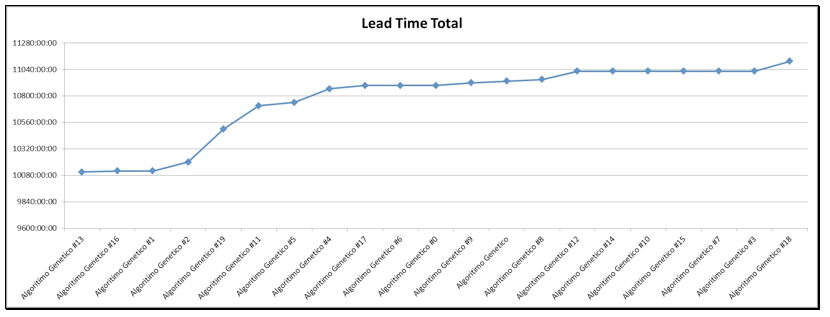
Fonte: O autor.

6. Conclusões

Adicionar caracteristicas reais de um processo de produção é fundamental para uma programação que se aproxime da realidade da fábrica. O método de busca CSP(Constraint Satisfaction Problem) permite com flexibilidade a modelagem de problemas, combinado com as caracteristicas do desenvolvimento orientado a objetos, que permite que todas as classes possuam a mesma interface, facilitando a interligação de clasess que representam restrições distintas sem a preocupação de qual o caminho para a solução. Permitiu também o uso de regras de liberação, demonstrado apenas com a regra SPT(shortest  process-time), mas podendo ser utilizada com diversas outras, presente na literatura. A implementação do AG como regra de despacho demonstra a flexibilidade do framework proposto na estratégia de programação das operações. Os resultados apresentaram boa concordância com os já reportados e o framework possibilitou uma modelagem mais simples dos problemas estudados, obtendo bons resultados na programação da produção. Como sugestão para trabalhos futuros indica-se a aplicação deste modelo em problemas mais complexos de programação da produção, utilização de técnicas de processamento em paralelo para solução das restrições bem como o uso de outras técnicas metaheurísticas como regras de despacho.

Referências bibliográficas

DUIN, C. W., SLUIS, E. V. (2006), "On the complexity of adjacent resource scheduling", Journal of Scheduling, 9 (1), 49–62.

FERNANDES, F. C. F.; FILHO, M. G.(2010)  "Planejamento e Controle da Produção: dos fundamentos ao Essencial". São Paulo: Editora Atlas.

FRAMINAN, J. M.; RUIZ, R. (2010)"Architecture of manufacturing schedulung systems: Literature review and an integrated proposal", European Journal Of Operational Research, 205, 237-246.

HVOLBY, H.-H.; STEGER-JENSEN, K. (2010). "Technical and industrial issues of Advanced Planning and Scheduling (APS) system", Computers in Industry, 61,  845-851.

MORAIS, M. F.; MENEGARDE, J. K.; CANTIERE, P. C. (2009); ".Regras de Prioridade e Critérios de Desempenho Adotados em Problemas de Programação da Produção em Ambientes Flow Shop". IV Encontro de Produção Cientifica e Tecnologia, 1-9.

SILVA, B. J. V. D.; MORABITO, R.; YANASSE, H. D. (2011); "Programação da Produção de gabaritos de montagem com restrições de adjacência na industria aéronáutica". Produção, 21, 696-707.

TUBINO, D. F. (2009) "Planejamento e Controle da Produção: Teoria e Prática". São Paulo: Editora Atlas, 190p.

TURATTI, R.; MARCANTONIO, R. (2009); "A Importância da Utilização dos Sistemas APS no Alinhamento de Estratégias Operacionais". SIMPOI, 1-9.

PEREIRA, V. O.; LIBRANTZ, A. F. H. (2013); " Framework computacional para programação da produção com capacidade finita', dissertação de mestrado, Universidade Nove de Julho, 110p.

WEGLAZ, J. ; JÓZEFOWSKA, J;  MIKA, M.; WALIGÓRA, G. (2011);"Project scheduling with finite or infinite number os activity processing modes – A survey", European Journal Of Operational Research, 208(3), 177-205.

XING, L.-N.; CHEN, Y.-W.; YANG, K.-W. (2009); "Multi-objective flexible job shop schedule: Design and evaluation by simulation modeling", Applied Soft Computing,  9(1), 362-376.

ZEBALLON, L. J. A (2010); "constraint programming approach to tool allocation and production scheduling in flexible manufacturing system". Robotics and Computer-Integrated Manufacturing, 26(6),725-743.

1. Universidade Nove de Julho – UNINOVE, Programa de Pós-Graduação em Engenharia de Produção (PPGEP), Email: valdecir@grv.com.br
2. Universidade Nove de Julho – UNINOVE, Programa de Pós-Graduação em Informática e Gestão do Conhecimento (PPGIGC), Email: librantz@uninove.br