Espacios. Vol. 36 (Nº 23) Año 2015. Pág. 6

Concentração de renda nos Municípios da Região Sul entre 2000 e 2010: Análise geográfica temporal utilizando a abordagem exploratória de dados espaciais

Concentration of wealth in the municipalities of the southern region between 2000 and 2010: Temporal geographic analysis using an exploratory approach of spatial data

Cleverson NEVES 1; Angelo RONDINA NETO 2; Emerson Guzzi Zuan ESTEVES 3; José Luiz PARRÉ 4; Antonio Edson AMARAL 5; Márcia Regina Gabardo da CAMARA 6

Recibido: 07/08/15 • Aprobado: 15/09/2015

Contenido

Introdução

1. Caracterização da Região Sul

2. Evolução das políticas sociais no Brasil

3. Metodologia: Análise espacial e o índice de Gini para distribuição de renda

4. Análise dos resultados

5. Considerações finais

Referências

Introdução

Conforme o primeiro relatório sobre o desenvolvimento humano para a América Latina e o Caribe, realizado pelo Programa das Nações Unidas para o Desenvolvimento (PNUD) em 2010, o Brasil possui um dos maiores índices de desigualdade do mundo – medido pelo índice de Gini. A análise permite verificar que, na América Latina, somente Bolívia (0,60) e Haiti (0,59) possuem índice de Gini superior ao Brasil (0,56). Em outros continentes, percebe-se que poucos países têm níveis próximos ao do Brasil, como é o caso na Ásia da Tailândia (0,59), que possui índice superior ao brasileiro. Na África percebe-se que vários países não tem uma desigualdade de renda em níveis próximos ao brasileiro. Entre os países desenvolvidos, o índice se localiza muito mais baixo. É o caso de países como a Dinamarca (0,27), Portugal (0,41) e os Estados Unidos da América (EUA) (0,40) (PNUD, 2014).

Os dados e a análise relativa permitem afirmar que o Brasil é um país significativamente desigual. Porém, deve-se levar em consideração que o país é continental e muito diverso, seja em termos geográficos, culturais, históricos e econômicos. Assim, é de se esperar que o índice de Gini também se revele diverso no país, como os pontos anteriores. Analisando-se os dados a nível estadual para o ano de 2009, por exemplo, vê-se que existem estados com índice de Gini inferiores ao nacional. É o caso de Santa Catarina (0,45), que possui níveis de desigualdade semelhantes aos países desenvolvidos (VIEIRA et al, 2011).

Essa desigualdade de renda e o elevado contingente de população pobre são considerados alguns dos principais problemas enfrentados atualmente no âmbito socioeconômico. Barros et al (2001) apontam que a condição de pobreza não se resume somente a uma definição, mas sim a uma condição em que a pessoa não consegue manter um padrão de vida satisfatório para arcar com suas necessidades básicas em um dado período.

Uma das medidas tomadas para confrontar essa questão é a intervenção do governo com políticas de transferência direta de renda para garantir à população mais vulnerável o nível mínimo dessa. Os programas inicialmente criados no final da década de 1990 foram, na década posterior, unificados no Programa Bolsa Família (PIRES, LONGO, 2008). Segundo Barros (2003), o Brasil conta atualmente com diversos programas sociais descentralizados. Nos últimos anos, o país apresenta sinais de melhora nos índices de pobreza, sendo que os programas de transferência de renda direta tiveram um papel importante para esse resultado.

Com base nessas considerações, pode-se chegar às questões: Como se evidencia a distribuição do índice de Gini especificamente nos municípios da Região Sul do Brasil? Quais as transformações na concentração de renda que se deram nesses municípios na década compreendida entre os anos de 2000 e 2010 – em que houve unificação dos programas de transferência de renda?

O presente trabalho tem o objetivo de responder essas perguntas. Ou seja, o objetivo é analisar as transformações ocorridas na concentração de renda (medida pelo índice de Gini) dos municípios da Região Sul do Brasil na década compreendida entre os anos de 2000 e 2010. Para tanto, será utilizada a metodologia de abordagem espacial e da análise univariada dos dados, permitindo analisar a trajetória do índice de Gini e agregar as informações sob a ótica espacial.

O artigo se divide em outras cinco seções além dessa introdução. Na seção 1 é apresentada uma caracterização dos estados da Região Sul. Na segunda seção é exposta a evolução das políticas sociais no Brasil, sobretudo na década analisada. A seção 3 tem como objetivo apresentar a metodologia desenvolvida pelo trabalho, ou seja, da análise exploratória dos dados espaciais e do índice de Gini, bem como a descrição da base de dados utilizada. Na quarta seção é apresentada as análises dos resultados. Por fim, são apresentadas as considerações finais do trabalho.

1. Caracterização da Região Sul

1.1. Paraná

De acordo com o censo demográfico de 2010 realizado pelo Instituo Brasileiro de Geografia e Estatística (IBGE), o Paraná apresentava 10.439.601 habitantes, totalizando 5,47% da população brasileira. A renda per capita era de R$ 16.928,00. Seu índice de desenvolvimento humano municipal (IDH-M), do PNUD era de 0,820, o menor dentre os Estados da Região Sul do Brasil.

A análise feita pelo Instituto Paranaense de Desenvolvimento Econômico e Social (IPARDES, 2014) mostra que de setembro de 2008, início da crise financeira mundial, a junho de 2009, 242 municípios dos 399 do Paraná obtiveram saldos positivos ou estáveis na geração de empregos. Ainda segundo o IPARDES (2014), a dinâmica da economia paranaense, fortemente influenciada pelo setor agropecuário, presenciou a redução da produção de soja e milho em 2009, impactando diretamente no resultado negativo de 1,2% do PIB do Estado. Em resumo, durante a crise internacional, a economia do Paraná decresceu mais do que a brasileira. Entretanto, no acumulado do emprego formal entre 2008 e 2010 a variação foi de 11,18%, próxima à média nacional (de 11,73%).

A crise também afetou as empresas do Paraná. Enquanto de 2003 a 2008 o número de empresas abertas no Estado aumentou em 30%, no mesmo período o número de empresas fechadas aumentou 99%, segundo dados da Junta Comercial do Paraná. Em 2008, foram criadas 40.664 empresas no Estado, mas 10.557 acabaram fechadas.

O comércio exterior paranaense também sentiu os efeitos da crise financeira internacional. Entre janeiro e julho de 2009, as exportações caíram 28,05% em relação ao mesmo período do ano anterior; e 42,64% na comparação entre julho de 2009 com o mesmo mês de 2008. No ano de 2009, o saldo acumulado em vendas ao exterior foi de US$ 6,8 bilhões. As importações, por sua vez, reduziram-se em 41,97% nos primeiros sete meses de 2009, resultando num saldo superavitário de US$ 2 bilhões (IPEA, 2009).

Entretanto, a indústria do Paraná alcançou a maior taxa de produtividade dentre os demais Estados brasileiros pesquisados (7,2%). Essa marca foi mais do que o dobro da registrada em 2007 (3,1%), sendo também a maior da série iniciada em 2002. Esse resultado foi obtido principalmente devido ao expressivo aumento da produção física (8,6%), o mais elevado dentre todos os Estado, muito acima da variação das horas pagas (1,3%). Contribuíram para essa performance as elevadas taxas de produtividade alcançadas pelos setores "Minerais não-metálicos" (20,8%) e "Madeira" (14,3%). Esse desempenho foi muito impactado, no caso do primeiro segmento, pelo aumento na produção física (25,4%) e, no caso do segundo, pela contração das horas pagas (-14,0%) (IBGE, 2014).

O IBGE adota uma subdivisão dos estados – as mesorregiões – que reúne municípios de uma área geográfica com similaridades econômicas e sociais. É empregada para fins estatísticos e não compõe, portanto, uma entidade política ou administrativa. Oficialmente, as dez mesorregiões do Estado do Paraná são: Centro Ocidental Paranaense; Centro Oriental Paranaense; Centro-Sul Paranaense; Metropolitana de Curitiba; Noroeste Paranaense; Norte Central Paranaense; Norte Pioneiro Paranaense; Oeste Paranaense; Sudeste Paranaense; e Sudoeste Paranaense (IPARDES, 2014). Essas mesorregiões são sintetizadas na Tabela 1, e apresentadas na Figura 1, no final da seção.

Tabela 1 - Mesorregiões do Paraná, quantidade de município e Microrregiões pertencentes

Fonte: IBGE, 2014.

1.2. Rio Grande do Sul

O Estado do Rio Grande do Sul é o mais meridional do Brasil, com papel destacado na história do país, uma vez que foi palco da Guerra dos Farrapos, a mais longa guerra civil do Brasil. É o segundo Estado brasileiro com mais presidentes da república na história do país, totalizando seis: Hermes da Fonseca, Getúlio Vargas, João Goulart, Costa e Silva, Emílio Médici e Ernesto Geisel.

O Estado ocupa uma área de 281.730,223 km, equivalente a pouco mais de 3% do território nacional (IBGE, 2014). De acordo com o Censo de 2010, o Rio Grande do Sul tinha uma população de 10.663.929 pessoas em 2010. Teve uma taxa de crescimento demográfico, entre 2000 e 2010, de 1,2% ao ano. De acordo com o censo demográfico de 2000, 80,8% da população do Estado morava na área urbana (IBGE, 2010). O IDH-M gaúcho, elaborado pelo PNUD, era de 0,746 em 2010.

Rio Grande do Sul é a quarta maior economia nacional, com 8,8% do PIB nacional – equivalente a R$ 252,483 bilhões (IBGE, 2014). A economia gaúcha tem ligação com os mercados nacional e internacional maior do que a média brasileira. Assim, ela tem oscilado conforme a evolução da economia brasileira bem como com a dinâmica das exportações.

Tabela 2 - Mesorregiões do Rio Grande do Sul, quantidade de município e Microrregiões pertencentes

Fonte: IBGE, 2014.

Conforme o IBGE (2014), no Estado do Rio Grande do Sul existem sete mesorregiões: Centro Ocidental Rio-Grandense, Centro Oriental Rio-Grandense, Metropolitana de Porto Alegre, Nordeste Rio-Grandense, Noroeste Rio-Grandense, Sudeste Rio-Grandense e Sudoeste Rio-Grandense. As mesorregiões se encontram sintetizadas na Tabela 2 e apresentadas, também, na Figura 1.

1.3. Santa Catarina

O Estado de Santa Catarina possui o maior PIB per capita da Região Sul e o quarto maior do Brasil. Ocupando apenas 1,2% do território nacional e com uma população em torno próxima dos 6 milhões de habitantes, o PIB do Estado atingiu, em 2008, mais de R$ 120 bilhões, aparecendo como o sexto maior dentre os estados brasileiros. O Estado é composto por 293 municípios, possuindo uma distribuição relativamente equilibrada, tanto da população como da atividade econômica, se comparado com os outros Estados (IBGE, 2014).

A forma geográfica do povoamento e colonização de Santa Catarina pode ajudar a explicar, em parte, o porquê de o estado vir apresentando o menor índice de concentração de renda dentre os Estados do Brasil, medido pelo índice de Gini. Dentro do processo de formação socioeconômica do Brasil, Santa Catarina é um caso à parte. Comparado às Regiões Norte e Nordeste, o Estado possui características divergentes, pois não teve na base de seu desenvolvimento raízes no latifúndio e no trabalho escravo e sim na pequena produção mercantil. Dessa originou-se os excedentes que possibilitaram a criação de importantes polos industriais que dinamizaram seu processo de desenvolvimento socioeconômico em relação às outras regiões do país – regiões essas que, em tese, não se observa um processo semelhante (VIEIRA et al, 2011).

Nas últimas décadas, os desequilíbrios regionais têm se mostrado de forma cada vez mais clara no Brasil e em seus Estados. Em Santa Catarina, em especial, houve a concentração da população e da atividade econômica em algumas regiões e a fuga da população e a estagnação ou declínio econômico em outras. Essa situação foi notável a ponto de estimular ações por parte do governo estadual que postulou como ação-base estimular a política de descentralização, uma tentativa de promover o desenvolvimento regional mirando à recuperação da harmonia na distribuição socioeconômica da população entre as regiões do Estado (RODOLFO; TEIXEIRA, 2011).

Em relação à atividade econômica, o estado conta com vários polos de significativa importância, dispostos por todo o território. Porém, pode-se notar a formação de arranjos produtivos bem definidos, de alcance regional e, em alguns casos, nacional. Os municípios mais importantes economicamente estão distribuídos por todas as regiões catarinenses.

Em termos populacionais, o maior município catarinense é Joinville, que em 2010 abrigava cerca de 515 mil habitantes – correspondendo a 8,24% da população do Estado. Isso contrasta com a maioria dos outros Estados brasileiros, em que a cidade mais importante economicamente detém um percentual muito maior da população estadual. Todavia, dos 293 municípios do Estado, 72,3% contavam, em 2010, com menos de 15 mil habitantes, o que pode contribuir para se entender a maneira como se sucedeu a distribuição espacial do desenvolvimento de Santa Catarina (RODOLFO; TEIXEIRA, 2011).

As mudanças ocorridas na economia catarinense se deram ao mesmo tempo em que se observaram as mudanças na distribuição da população espacialmente. Na medida que a atividade econômica de uma região entra em decadência, ou sofre contínuo processo de modernização produtiva, são criadas as circunstâncias que fazem com que parte dos habitantes tenham sua base de existência prejudicada. A esses restam algumas alternativas como migrar para outras regiões economicamente mais dinâmicas, ou buscar a especialização de mão de obra em busca de novas oportunidades (SINGER, 1990).

Conforme Singer (1990), associam-se as migrações à ação de dois fatores: os de estagnação e os de mudança. Os fatores de estagnação estão relacionados à escassez de recursos – como terra e capital – que geram a impossibilidade de se obter ganhos de produtividade. Por sua vez, os fatores de mudança estariam ligados à implementação de relações capitalistas na área de origem dos fluxos, aumentando a produtividade e criando uma população sobrante que poderia ser deslocada para outras áreas. Os fluxos gerados por esses fatores, nas áreas de origem, seriam orientados pela ação de fatores de atração – que podem ser desde a estrutura de oferta de serviços públicos, opções de lazer, ou à demanda por força de trabalho, elemento mais comum.

Conforme a divisão do IBGE (2014), o Estado de Santa Catarina se divide em 6 mesorregiões: Grande Florianópolis, Norte Catarinense, Oeste Catarinense, Serrana, Sul Catarinense e Vale do Itajaí. As mesorregiões são sintetizadas na Tabela 3 e apresentadas na Figura 1

Tabela 3 - Mesorregiões de Santa Catarina, quantidade de município e Microrregiões pertencentes

Fonte: IBGE, 2014

-----

Figura 1 - Mesorregiões da Região Sul do Brasil

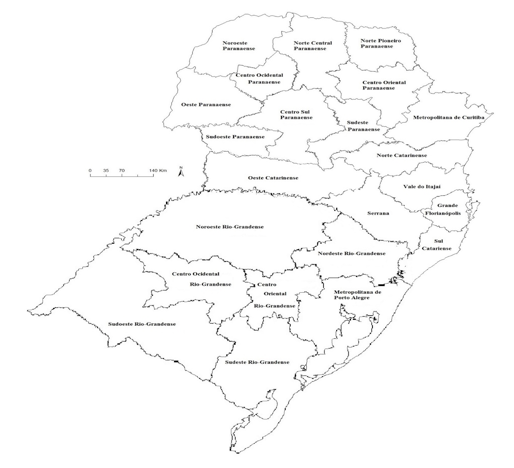
Fonte: Elaborado pelos autores a partir de IBGE (2014).

2. Evolução das políticas sociais no Brasil

Nos últimos dez anos a realidade brasileira passou por transformações intensas. O Brasil avançou, desenvolveu-se e ampliou os diretos a seus cidadãos. A intensidade desses avanços sociais decorre, sobretudo, dos efeitos sinergéticos de decisões eficazes de políticas públicas ao longo dos anos 2000. Dentre essas, cabe destacar o fortalecimento da agenda de políticas voltadas à universalização dos direitos sociais e a inclusão de segmentos populacionais historicamente excluídos. A implementação de políticas públicas articuladas entre as esferas de governo contribuiu para se resgatar a ampliação da capacidade de planejamento e investimento do Estado brasileiro, bem como contribuiu ao fortalecimento do mercado interno.

Conforme Fernandes (2006), a justiça social encontra-se nas constituições em praticamente todos os países, cabendo ao Estado formular as políticas sociais. Em uma análise histórica, o autor aponta que na década de 1970 os Estados Nacionais passaram por crises fiscais e de endividamento que comprometeram o financiamento de políticas sociais. A partir das décadas de 1980 e 1990, os Estados Nacionais buscam alternativas de gestão para financiar suas políticas públicas. Dessa forma, para que haja uma boa administração pública é necessário que o processo político feito pelos participantes das arenas de decisão política seja de qualidade.

Para Silva et al (2004), durante o governo de Fernando Henrique Cardoso a principal prioridade foi o ajuste e a estabilidade econômica, ficando as questões sociais em um segundo plano. Todavia, a partir de 2001 o governo cria a "rede de proteção social", com programas destinados às famílias pobres, na categoria Renda Mínima, sendo o Bolsa Escola a nível nacional, acompanhado de outros programas a níveis municipais e estaduais. Esses começaram em 1995, sendo exemplos: o programa de Garantia de Renda Familiar Mínima de Campinas/SP, também adotado em Ribeirão Preto/SP; o programa Bolsa-Escola, adotado em Brasília/DF; e o programa "Nossa Família", adotado por Santos/SP.

Barros et al (2001) enfatizam que o Brasil no início do século XXI não era um país pobre, mas um país com grande número de pobres e com muita injustiça e desigualdade. Para os autores, é necessário um processo democrático com eficiência econômica e justiça social; um desafio na era moderna do país, que leva o Brasil a ter inovações em suas políticas, por meio dos programas sociais.

3. Metodologia: Análise espacial e o índice de Gini para distribuição de renda

3.1. Análise exploratória dos dados espaciais

A análise exploratória dos dados espaciais pode ser realizada sempre que as informações estiverem espacialmente localizadas e for necessário considerar a importância do arranjo espacial na análise e interpretação dos resultados. Seu objetivo é aprofundar a compreensão do objeto de análise e avaliar hipóteses a ele relacionadas, ou, ainda, tentar prever valores em áreas onde as observações não estão disponíveis. (BAILEY; GATTREL, 1995).

Anselin (1999) classifica a análise exploratória dos dados espaciais como a coleção de técnicas para descrever e visualizar as distribuições espaciais, identificar localidades atípicas – os outliers espaciais –, descobrir padrões de associação espacial – clusters espaciais – e evidenciar diferentes regimes espaciais e outras formas de instabilidade.

Conforme Almeida (2012, p. 104), a primeira etapa nos estudos exploratórios dos dados espaciais é testar a hipótese de que os dados estão distribuídos aleatoriamente. A análise dessa hipótese permite a verificação se os valores de algum atributo em uma região dependem ou não dos atributos das regiões vizinhas (ou seja, que há influência espacial). Para tanto, esse teste de hipótese leva em consideração a estatística I de Moran.

Estatística I de Moran

Almeida (2012, p. 105) apresenta a estatística I de Moran como um coeficiente de autocorrelação espacial que utiliza a medida de autocovariância na forma de produto cruzado [7].

Algebricamente, a estatística I de moral é dada pela equação (1):

Ou, matricialmente, tem-se pela equação (2):

Nas equações,  representa o número de regiões,  os valores das variáveis de interesse padronizadas e  os valores médicos da variável de interesse padronizada nos vizinhos, definidos de acordo com uma matriz de ponderação espacial . Nessa matriz, o elemento referente à uma região "" e uma região "" é registrado como . Ainda, nas equações o elemento  representa a operação de soma, significando que todos os elementos da matriz de pesos espaciais  devem ser somados.

De acordo com Almeida (2012) o I de Moran fornece três tipos de informações:

1. O nível de significância que reforça a informação sobre os dados estarem distribuídos aleatoriamente ou não;
2. O sinal positivo da estatística I de Moran, desde que significativos, indica que os dados estão concentrados através das regiões. O sinal negativo, por sua vez, indica a dispersão dos dados;
3. A magnitude da estatística fornece a força da autocorrelação espacial, quanto mais próximo de um mais forte é autocorrelação e quanto mais próximo de -1 mais disperso estará os dados.

Conforme Almeida (2012), uma maneira usual de se visualizar a autocorrelação espacial evidenciada pelo I de Moran é, também, o diagrama de dispersão de Moran.

3.1.2. Diagrama de dispersão de Moran

O diagrama de dispersão de Moran apresenta a defasagem espacial da variável de interesse no eixo vertical e o valor de fato da variável no eixo horizontal.

Além da medida global de associação linear espacial, o diagrama fornece outras informações, sobre o tipo de associação, em cada um dos quadrantes – a saber, Alto-Alto (AA), Alto-Baixo (AB), Baixo-Alto (BA) e Baixo-Baixo (BB). A Figura 2 apresenta o exemplo de um diagrama de dispersão de Moran

Figura 2 – Diagrama de Dispersão de Moran

Fonte: Almeida (2012).

Assim, um agrupamento do tipo Alto-Alto (AA) apresenta que as unidades espaciais pertencentes a esse exibem valores altos das variáveis de interesse, estando rodeadas por unidades espaciais que também apresentam valores altos – primeiro quadrante do diagrama. O tipo de agrupamento Baixo-Baixo (BB) se refere aos agrupamentos em que as unidades espaciais apresentam valores baixos nas variáveis de referência e são circundadas por outras com valores também baixos – terceiro quadrante do diagrama.

De maneira semelhante, os agrupamentos Alto-Baixo (AB) são aqueles em que a unidade espacial evidencia alto valor em uma das variáveis de interesse e um baixo valor nas unidades espaciais que a circundam – quarto quadrante do diagrama. Por fim, o agrupamento Baixo-Alto (BA) é aquele em que a unidade espacial apresenta um baixo valor na variável de interesse e está circundado por unidades espaciais que apresentam um valor alto valor – segundo quadrante do diagrama.

3.1.3. Indicadores locais de associação espacial (LISA) [8]

Os indicadores LISA indicam o grau de associação espacial local. Conforme Anselin (1999), para que isso ocorra faz-se necessário que a estatística satisfaça dois critérios:

Deve possuir, para cada observação, uma indicação de clusters espaciais que sejam significativos estatisticamente;

O somatório dos indicadores locais, para todas as regiões, deve ser proporcional ao indicador de autocorrelação espacial global.

Dessa forma, os indicadores LISA podem ser representados por meio da equação (3):

Na equação (3),  corresponde à variável de interesse na região "" para o ano "",  é média das observações entre as regiões para o ano "", em que o somatório da relação para "" é tal que somente os valores vizinhos de "" são incluídos.

Conforme Anselin (1999), a estatística LISA é usada para testar a hipótese nula de ausência de associação espacial local. Dessa forma, deve-se fazer uso de uma aleatorização condicional que permita determinar pseudoníveis de significância. Para se obter uma distribuição empírica das estatísticas de teste deve-se observar se o valor da variável de interesse está localizado dentro ou fora da região crítica definida. Assim, caso o valor calculado for superior em magnitude à esperança matemática do I de Moran, seus resultados serão, então, estatisticamente significativos.

3.2. Índice de Gini e sua decomposição

O índice de Gini, criado pelo matemático italiano Conrado Gini, é um instrumento utilizado para medir o grau de concentração de renda em determinado grupo, ou seja, a diferença entre os rendimento dos mais pobres e dos mais ricos. Numericamente, o índice varia de 0 (zero), situação em que todos estão em igualdade, a 1 (um), em que uma só pessoa deteria toda a riqueza.

Na prática, o indicador é muito utilizado para comparar os 20% mais pobres com os 20% mais ricos. No Relatório de Desenvolvimento Humano de 2014, elaborado pelo PNUD, o Brasil aparece na 79ª posição dentre 187 países no valor do Índice de Desenvolvimento Humano (IDH) de 0,744. Todavia, quando descontado o valor do IDH em função da desigualdade presente no país, o índice fica 27% menor (0,542) (PNUD, 2014).

Conforme Pires e Longo (2008), os programas de transferência de renda são programas sociais – com uma intervenção do governo na economia nacional – voltados para resultados imediatos de combate à pobreza e à concentração de renda. Para tais fins, segundo os autores, é necessário que haja uma maior participação do setor privado nos programas sociais e também uma boa eficiência na alocação dos recursos, de forma a garantir aos indivíduos as suas necessidades básicas. Espera-se, assim, a integração dos indivíduos, antes afastados, na vida econômica moderna. Todavia, nem sempre os programas sociais adotados alcançam os resultados esperados.

3.2.1. Evolução recente do índice de Gini nas Regiões Brasileiras

Conforme dados do Atlas de Desenvolvimento Humano do PNUD e do IBGE, a melhoria do perfil distributivo da renda no Brasil é revelado na trajetória declinante do índice de Gini entre 2001 e 2011 para todas as Regiões brasileiras, conforme a Figura 3 .

Figura 3 - Evolução do índice de Gini por Região Brasileira entre 2000 e 2011*

Nota: * Rendimento Mensal Domiciliar. ** Norte Urbano
Fonte: Elaborado pelos autores com base nos dados da PNUD (2014).

Nas Regiões Sul e Sudeste o índice de Gini caiu para um patamar inferior a 0,5. Esse nível ainda é elevado se comparado internacionalmente, porém se mostra significativo se analisado o seu histórico anterior. Nas Regiões Centro-Oeste e Nordeste, que mantinham o pior quadro distributivo entre as regiões brasileiras em 2001, o índice convergiu para o patamar de 0,5 – situação semelhante à Região Norte.

3.2.2. Decomposição do Coeficiente de Gini

Shorrocks (1982) demonstrou que o Coeficiente de Gini pode ser decomposto por componentes de renda, bem como que a expressão resultante depende dos coeficientes de concentração de cada componente e de seu peso na renda total, como dado na equação (4):

Na equação (4), "" é o coeficiente de Gini, "" é o coeficiente de concentração da renda "" relativo à renda total e "" é o peso da renda "" na renda total.

No presente artigo, especificamente, utilizou-se a decomposição do coeficiente de Gini da distribuição de renda domiciliar per capita. Esse método corresponde na apuração das rendas médias de cada centésimo da distribuição da renda domiciliar per capita e de seus componentes.

Por sua vez, o impacto dos programas de Transferência Condicionadas pela Renda (PTCR) sobre a distribuição de renda pode ser calculado por diversos métodos. Para fins do trabalho, os vários tipos de rendas individuais foram agregados em quatro componentes:

1. Renda do trabalho;
2. Renda da Seguridade Social;
3. Renda dos PTCRs; e
4. Outras (como aluguéis, juros, doações etc.).

   3.3. Descrição da base de dados

Para os fins do trabalho, foram utilizados dados do IBGE, do Ministério do Desenvolvimento Social (MDS), da Matriz de Desenvolvimento Social, do Instituto de Pesquisa Econômica Aplicada (IPEA), PNUD. Foram utilizados o índice de Gini dos anos 2000 e 2010 para os municípios da Região Sul do Brasil.

4. Análise dos resultados

Nesta seção realiza-se a análise exploratória dos dados espaciais do índice de Gini para os anos de 2000 e 2010 para os estados da Região Sul do Brasil.

4.1. Resultados encontrados para a Região Sul

4.1.1. I de Moran Global Univariado

Segundo Almeida (2012), quando o valor do I de Moran calculado for maior do que o I de Moran esperado, indica-se a presença de autocorrelação espacial positiva. Entretanto, no caso do I de Moran calculado ser menor do que o I de Moran esperado, esse apresentará uma autocorrelação negativa.

A autocorrelação espacial global univariada possibilita identificar se a variável observada em determinada região tem alguma associação em relação a mesma variável em regiões ou municípios vizinhos. O I de Moran esperado é dado pela expressão matemática, , a qual fornece o valor que seria obtido caso não houvesse padrão espacial nos dados.

Em relação ao presente trabalho, ambos anos apresentaram a mesma esperança para o I de Moran, sendo E(I2000;2010)= -0,0034. Comparando com o valor do I de Moran para o ano 2000 (0,329988) e para o ano de 2010 (0,35926), nota-se que os valores computados são maiores que a esperança (-0,034). Ou seja, ambos coeficientes apresentam clara indicação de que o Índice de Gini é autocorrelacionado no espaço através dos municípios da Região Sul. Entretanto, é oportuno salientar que o I de Moran apresentou uma pequena elevação ao longo da década, registrando um aumento de (0,029272), demonstrando que houve uma maior concentração de renda em algumas regiões dos estados da região Sul ao longo da década, pelo provável aumento no número e no tamanho dos clusters observados. Sendo assim, pelos valores encontrados, a correlação existente na pesquisa demonstra que os municípios com um índice de Gini acima (abaixo) da média – ou seja, alto (baixo) – são vizinhos de municípios com um alto (baixo) índice de Gini – ou seja, acima (abaixo) da média registrada para a Região Sul.

A Tabela 4 apresenta os valores do I de Moran da variável Gini para a matriz de pesos espaciais do tipo Rainha (Queen) para os anos de 2000 e 2010. O sinal positivo da estatística I de Moran da Tabela 4 indica que os dados estão concentrados nos municípios – ou seja, correlacionados positivamente –, sendo possível observar o grau de associação espacial existente a uma probabilidade de 1% de significância.

Tabela 4 - Coeficiente univariado I para índice de Gini nos anos de 2000 e 2010

Nota: Pseudosignificância empírica baseada em 999 permutações aleatórias.
Fonte: Elaborado pelos autores com base nos dados do IBGE e MDS

Analisando comparativamente os coeficiente univariados I, para os anos de 2000 e 2010, pode-se observar uma maior ampliação da associação espacial. Ou seja, tem-se uma elevação na concentração espacial em relação ao índice pressuposto (Gini) nos municípios da Região Sul ao longo da década. A magnitude da estatística I fornece a força da autocorrelação. Ou seja, quanto mais próximo de 1 (um), mais forte a concentração, e quanto mais próximo de -1 (menos um), mais dispersos estão os dados.

Como Haddad e Pimentel (2004), explicam que a análise da estatística I de Moran respeita os preceitos da existência de regimes espaciais, mas não torna possível a visualização de onde estão esses regimes e sua evolução ao longo do tempo. Para isso será utilizado o diagrama de Moran.

Figura 4 - Diagrama de Dispersão de Moran Univariado do índice de Gini dos municípios da Região Sul de 2000 e 2010

Fonte: Elaborado pelos autores com base nos dados do IBGE e MDS.

4.1.2. I de Moran Local

Conforme Almeida (2012), pode-se também se realizar um mapeamento de que os valores da probabilidade medida sejam estatisticamente significativos, gerando um mapa de significância de Moran Local.

A Figura 5 apresenta a significância das unidades espaciais através da estatística I de Moran univariada local para o índice de Gini analisado. As cores indicam o nível de significância; quanto mais próximo do verde claro, menor a significância, até o verde escuro, que evidencia o maior nível de significância. Dessa forma, os valores variam de 0,01% a 5% de significância, com os municípios em cor branca aqueles que não são significativos.

Figura 5 - Mapa de Significância LISA Univariada do índice de Gini da Região Sul de 2000 e 2010

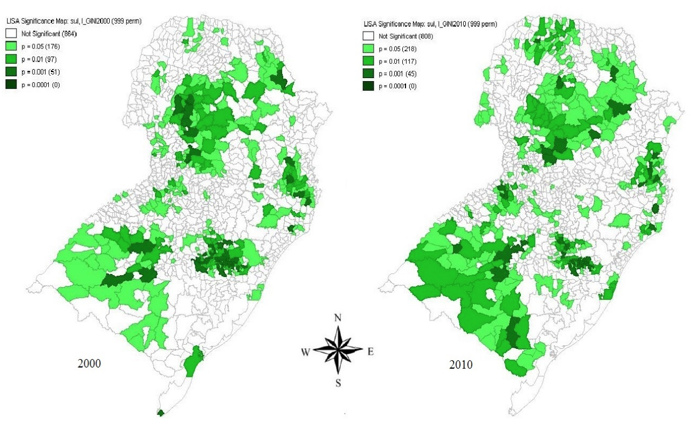
Fonte: Elaborado pelos autores com base nos dados do IBGE e MDS.

A Figura 6 na sequencia evidencia as aglomerações – clusters – univariadas que apresentam significância para o I de Moran Local.

De acordo com Almeida (2012), o mapa de clusters apresenta as quatro categorias estatisticamente significantes, combinando o mapa de significância local com o diagrama de dispersão de Moran.

De maneira geral, ao analisar os mapas de clusters para 2000 e 2010, percebe-se uma ampliação das aglomerações do tipo Alto-Alto, sobretudo na região central do Estado do Paraná e na região Oeste, Sudoeste e Sudeste de Rio Grande do Sul.

Pode-se visualizar também a concentração de três áreas de aglomerações Baixo-Baixo – norte/noroeste do Paraná, na parte leste de Santa Catarina e na parte nordeste do Rio Grande do Sul. A seguir, analisar-se-ão os resultados dos estados que compõem a Região Sul a nível de mesorregião.

Figura 6 - Mapa de Cluster Univariado do índice de Gini da Região Sul nos anos 2000 e 2010

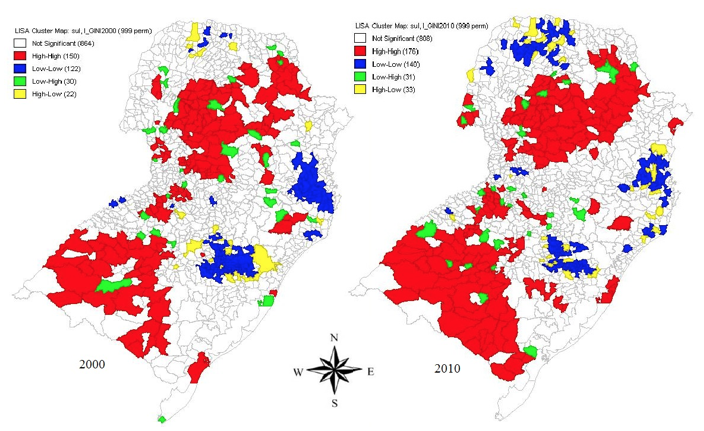
Fonte: Elaborado pelos autores com base nos dados do IBGE e MDS.
Análise dos resultados para os estados

4.2.1. Paraná

No estado do Paraná, pode-se constatar que, na Mesorregião Metropolitana de Curitiba, a cidade de Curitiba apresentava uma relação Alto-Baixo significativa. Já em 2010, Paranaguá apresentou uma relação Alto-Alto significativa.

Nas Mesorregiões Centro-Oriental Paranaense, Sudeste Paranaense, Centro-Sul paranaense, percebe-se um aumento da relação Alto-Alto entre 2000 e 2010.

Já na Mesorregião Norte-Pioneiro Paranaense, alguns municípios que eram Baixo-Alto em 2000 deixaram de ser significativo em 2010, evidenciando um aumento da presença de aglomerações Alto-Alto significativas.

Nas Mesorregiões Norte-Central Paranaense, Noroeste Paranaense houve uma melhora da relação de municípios Baixo-Baixo, aumentando a significância em 2010. Também houve um aumento da presença de municípios do tipo Alto-Baixo.

A Mesorregião Oeste Paranaense apresentou o surgimento municípios com uma relação Alto-Alto e Baixo-Alto de uma maneira mais intensa em 2010 do que em 2000.

Na Mesorregião Sudoeste Paranaense observa-se que dois municípios, antes do tipo Baixo-Alto em 2000, deixaram de ser significativos em 2010.

Por fim, a Mesorregião Centro-Ocidental Paranaense apresentou uma estabilidade nos dados entre 2000 e 2010.

4.2.2. Rio Grande do Sul

Pode-se verificar, para o estado do Rio Grande do Sul, que as Mesorregiões Metropolitana de Porto Alegre, Nordeste Rio-Grandense, Centro-Oriental Rio-Grandense apresentaram uma diminuição dos municípios com relação Baixo-Baixo e também de municípios Alto-Baixo em 2010. Houve também um município Baixo-Alto que passou a ser Alto-Alto. No sul da mesorregião Centro-Oriental Rio-Grandense, especificamente, surgiram municípios com relação Alto-Alto em 2010 que não apareciam anteriormente em 2000.

Nas Mesorregiões Centro-Ocidental Rio-Grandense, Sudoeste Rio-Grandense e Sudeste Rio-Grandense houve um grande aumento da relação Alto-Alto, apesar de surgir um pequeno acréscimo de municípios Baixo-Alto.

A Mesorregião Noroeste Rio-Grandense apresentou aumento no número de municípios Alto-Alto e Baixo-Alto, e alguns poucos que eram Baixo-Baixo deixaram de ser significativos.

4.2.3. Santa Catarina

Ao se analisar o estado de Santa Catarina, pode-se verificar uma redução dos municípios Baixo-Baixo em 2010 das Mesorregiões Norte Catarinense, do Vale do Itajaí e da Grande Florianópolis. Pode-se perceber também o surgimento em 2010 de aglomerações do tipo Alto-Baixo, quadro que não se verificava em 2000.

Na Mesorregião Oeste Catarinense é possível notar uma redução de municípios que apareciam com relação Alto-Alto significativa em 2010. Há, inclusive, o aparecimento de uma aglomeração Baixo-Baixo no último período.

Na Mesorregião Serrana, percebe-se que grande parte das aglomerações passaram a não ser significativas, sobretudo os municípios que apareciam em 2000 como Baixo-Alto.

Por fim, na Mesorregião Sul Catarinense pode-se verificar que os dados permanecem relativamente estáveis ao se analisar os cenários para 2000 e 2010.

5. Considerações finais

Esse estudo teve como objetivo verificar qual o padrão locacional do índice de Gini, para os municípios da Região Sul nos anos 2000 e 2010, analisando a autocorrelação espacial e a presença de clusters espaciais entre os municípios. Através da análise exploratória de dados espaciais identificou-se que, em geral, os municípios com alto índice de Gini são vizinhos de outros municípios com a mesma característica, assim como os municípios com baixo índice de Gini são cercados por municípios nas mesmas condições.

Analisa-se, através da técnica exploratória de dados espaciais, que no decorrer dos anos que houve um aumento da autocorrelação positiva do índice de Gini para os municípios da Região Sul entre 2000 e 2010, identificando clusters Alto-Alto e Baixo-Baixo maiores em 2010.

No Paraná observou-se um aumento significativo dos municípios com relação Alto-Alto, sobretudo nas mesorregiões Centro-Oriental Paranaense, Centro-Sul Paranaense e Sudeste Paranaense, e uma melhora da relação Baixo-Baixo e Alto-Baixo nas mesorregiões Norte Central Paranaense e Noroeste Paranaense.

No Rio Grande do Sul constatou-se uma elevação significativa dos municípios com relação Alto-Alto nas mesorregiões Centro Ocidental Rio-Grandense, Sudeste Rio-Grandense e Sudoeste Rio-Grandense, bem como uma diminuição no número de municípios na relação Baixo-Baixo e Alto-Baixo nas mesorregiões Nordeste Rio-Grandense e Metropolitana de Porto Alegre.

Pode-se apontar para o estado de Santa Catarina que a concentração de municípios com os maiores valores do índice de Gini, localiza-se na Mesorregião Oeste Catarinense, e a concentração de municípios com os menores valores de Gini alocam-se nas Mesorregiões do Vale do Itajaí, Norte Catarinense e Grande Florianópolis. Embora na parte nordeste da Mesorregião Norte Catarinense, na Mesorregião Serrana e na parte norte da Mesorregião Oeste Catarinense apresentar uma redução no decorrer da década do número de municípios atípicos do tipo Baixo-Alto e Alto-Baixo, houve também um aumento, embora disperso, dos clusters do tipo Alto-Alto.

Contudo, ao analisar os resultados encontrados, pode-se enfatizar que, nas regiões em que ocorrem um bom processo de industrialização e de ganhos tecnológicos, há a criação à sua população de acesso a mais oportunidades de melhores rendimentos, possibilitando, assim, uma melhor desconcentração de renda entre os indivíduos.

Referências

ALMEIDA, Eduardo.  Econometria Espacial Aplicada. Campinas: Editora Alínea, 2012.

ANSELIN, L. Spatial Econometrics. Texas: Klumer academic publishers, 1999.

BAILEY, T.C., GATRELL, A.C. Interactive Spatial Data Analysis, Prentice Hall. 1995.

BARROS, R. P. Desafios para a Política Social Brasileira. Rio de Janeiro: IPEA, texto para discussão, n. 985, out. de 2003.

BARROS, R. P.; HENRIQUES, R.; MENDONÇA, R. A Estabilidade Inaceitável: Desigualdade e Pobreza no Brasil. Rio de Janeiro, IPEA, texto para discussão, n. 800, jun. de 2001.

DINIZ, S. S. Análise espacial da produtividade de laranja dos municípios do estado de São Paulo: 2002-2010. 2012. 118 f. Dissertação (Mestrado Economia Regional) - Universidade Estadual de Londrina. Londrina, 2012.

FERNANDES, R. G. Programa Bolsa Família: Promoção de Cidadania?. 2006. Disponível em: <http://web.intranet.ess.ufrj.br/monografias/102053814.pdf>. Acesso em: 07 nov. 2014.

HADDAD, E. A.; PIMENTEL, E. A. Análise da distribuição espacial da renda no estado de Minas Gerais: Uma abordagem setorial. São Paulo, 2004.

IBGE. Instituto Brasileiro de Geografia e Estatística. Disponível em: <www.ibge.gov.br/cidades >.  Acessado em 07 nov. 2014.

IPARDES. Municípios e cidades. Disponível em: <www.ipardes.gov.br/cidades>. Acesso em: 07 nov. 2014.

IPEA. A crise internacional e possíveis repercussões: primeiras análises. Brasília: IPEA, 2009.

PIRES, D. C. A.; LONGO, L. A. F. de B. A implantação do Bolsa Família e sua relação com a pobreza nas regiões brasileiras no período de 2004 e 2006. Bahia Análise & Dados, Salvador, v. 18, n. 1, p. 007-021, abr./jun. 2008.

PNUD – Programa das Nações Unidas Para o Desenvolvimento. Disponível em; <http://www.pnud.org.br/rdh>. Acesso em: 07 nov. 2014.

RODOLFO, F. ; TEIXEIRA, Felipe Wolk. Santa Catarina: Desigualdades Regionais no Contexto de Descentralização. In: V Encontro de Economia Catarinense, 2011, Florianópolis. V Encontro de Economia Catarinense, 2011.

SILVA, M. O. da S.; YASBEK, M. C.; GIOVANNI, G. di. A Política Social Brasileira no Século XXI: a prevalência dos programas de transferência de renda. São Paulo: Cortez, 2004.

SINGER, Paul. A economia política da urbanização. São Paulo: Brasiliense, 1990.

SHORROCKS, A. Inequality decomposition by factor components. Econometria, v. 50, n.11, p. 193-211, 1982.

VIEIRA, P.A. ; SILVA, L. M. F. ; REDIVO, A. S. . A formação socioeconômica de Santa Catarina ajuda a explicar porque o estado apresenta a menor concentração de renda do Brasil?. In: V Encontro de Economia Catarinense, 2011, Florianópolis. Encontro de Economia Catarinense, 2011.

1. Professor Mestre em Economia Regional do Departamento de Economia da UEL. E-mail: cleversonneves@uel.br.
2. Doutorando pelo programa de Pós-Graduação em Economia (PCE) da UEM. E-mail: angelorondina@gmail.com
3. Doutorando do Programa de Pós-Graduação em Economia (PCE) da UEM. E-mail: esteves@sercomtel.com.br
4. Professor Doutor Titular do programa de Pós-Graduação (PCE) da UEM. E-mail: jlparre@uem.br
5. Doutor em Teoria Econômica pelo programa de Pós-Graduação (PCE) da UEM. E-mail: amaral@uel.br
6. Professora Doutora Titular do Programa de Mestrado Economia Regional – (UEL) e-mail: mgabardo@uel.br

7. A estatística leva o nome de Patrick A. P. Moran que, em 1948, propôs o primeiro coeficiente de autocorrelação espacial.

8. Do inglês Local Indicator of Spatial Association (LISA).