HOME | ÍNDICE POR TÍTULO | NORMAS PUBLICACIÓN

Espacios. Vol. 36 (Nº 20) Año 2015. Pág. 17

Simulação da dinâmica operacional do processo de esquartejamento de suínos e avaliação do peso final dos principais cortes

Simulation of operating dynamics of the quartering process of swine and evaluation of the final weight of the main cuts

Vanessa Angélica GONÇALVES 1, Genilso Gomes de PROENÇA, José Airton Azevedo dos SANTOS; Carla Adriana Pizarro SCHMIDT 2

Recibido: 26/06/15 • Aprobado: 09/07/2015

Contenido

1. Introdução

2. Materiais e métodos

3. Resultados e discussão

4. Conclusões

Referencias bibliográficas

1. Introdução

O Brasil é o quarto maior exportador mundial de carne suína e possui um dos maiores rebanhos de suínos do mundo. Segundo os dados apresentados pelo IBGE (2015) a quantidade de carcaças abatidas no ano de 2014, indicou a região sul do país como a principal produtora de carne suína. Sendo que, o estado de Santa Catarina foi o maior produtor, contabilizando 9.424.738, Rio Grande do Sul em segundo 8.011.700 e o Paraná em terceiro com 6.920.787 animais abatidos.

Atualmente a suinocultura é um importante fator do desenvolvimento econômico nacional, provocando efeitos multiplicadores de venda em todos os setores da economia, intensificando a demanda por insumos agropecuários e modernização das agroindústrias (Lima, 2010).

Na área alimentícia, trabalha-se cada vez mais com entregas mais frequentes e tempos de produção mais reduzidos. Assim, é preciso que o processo de esquartejamento de suínos seja organizado de modo que as perdas sejam mínimas, tanto de tempo como de produto. Para obter este resultado, diversas técnicas são disponibilizadas aos dirigentes desses processos, uma delas é a simulação computacional (Fernandes, 2006).

A simulação, utilizando modelos computacionais, torna possível analisar um sistema real, virtualmente, sem a necessidade de interferir nas suas atividades. A simulação de um modelo permite entender a dinâmica de um sistema assim como analisar e prever o efeito de mudanças que se introduzam no mesmo. É uma representação próxima da realidade, e será tanto mais real quanto mais características significativas do sistema seja capaz de representar (Miyagi, 2006; Alves et al., 2014; Baumgartner et al., 2013).

O controle Estatístico de Processos (CEP) é uma ferramenta que auxilia na obtenção de valores limites para o processo, auxilia ainda na detecção de comportamentos tendenciosos. Dentro deste contexto, os gráficos de controle são considerados uma das suas ferramentas mais importantes. Os gráficos de controle são elementos visuais para o monitoramento da conformidade de características de produtos e processos (Alencar et al., 2007).

O presente estudo objetivou conhecer e analisar o processo de esquartejamento de suínos de uma agroindústria do estado do Paraná por meio de controle estatístico do processo, avaliando os limites e a padronização de peso dos cortes suínos utilizados pela empresa bem como pela avaliação da linha através de técnicas de simulação.

2. Materiais e métodos

O frigorifico, em estudo, localiza-se no estado do Paraná, possui mais de 400 colaboradores e abate mais de 1500 suínos por dia. Neste trabalho analisou-se especificamente a linha de esquartejamento do frigorifico, por meio de técnicas de análise estatística e simulação. A Figura 1 ilustra o processo de esquartejamento de carcaças suínas.

Figura 1 - (a) Mesa rolante para cortes de carcaças de suínos e (b) Linha de esquartejamento de carcaças suínas.
Fonte: Multinox – Equipamentos agroindustriais (2014).

2.1 AVALIAÇÃO DOS PESOS DE CORTES DE SUÍNOS

Para coleta dos pesos foram escolhidos aleatoriamente, na linha de produção, 100 cortes de cada um dos quatro principais cortes suínos da empresa, a saber Paleta, Pernil, Barriga com Costela e Carré com Sobre Paleta. Para pesagem utilizou-se uma balança da marca Filizola do modeloTR 307580, testada e aprovada pelo INMETRO. Os dados foram anotados e posteriormente tabulados no software Microsoft Excel®. Na sequência, os dados (pesos) foram submetidos à análises de estatística descritiva e controle estatístico por meio do software Action® 2.7.

2.1.1 Gráficos de controle

Todo processo apresenta variabilidade, parte dela sendo originada por elementos vitais ao processo, como matérias-primas, máquinas, métodos, gerenciamento e mão-de-obra. Esta variabilidade pode ser constada através de gráficos de controle. Estes gráficos auxiliam na verificação da estabilidade do processo.

Os gráficos de controle (Figura 2) são compostos de três linhas paralelas, a linha central (LC), o limite superior de controle (LSC) e o limite inferior de controle (LIC).

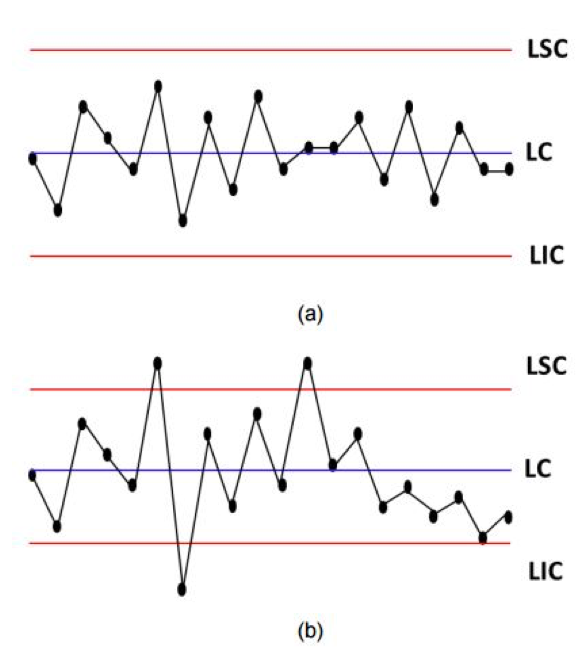
Figura 2 - Gráficos de Controle: (a) sob controle estatístico e (b) fora de controle estatístico.

Quando todos os pontos amostrais estiverem dispostos dentro dos limites de controle de forma aleatória, considera-se que o processo está "sob controle" (Figura 2a). No entanto, se um (ou mais) ponto(s) estiver(em) disposto(s) fora dos limites de controle, há evidência de que o processo está "fora de controle" (Figura 2b), e que a investigação e tomada de ação(ões) corretiva(s) se faz necessária para detectar e eliminar a(s) causa(s) especiais no processo (Oliveira, 2013).

2.2 SIMULAÇÃO COMPUTACIONAL

No planejamento da coleta de dados para simulação concluiu-se que seria necessário determinar as seguintes variáveis: Tempo de Corte das paletas (TC); Tempos de Acabamento das paletas (TA) e Tempos de processo no Mezanino (TM). Alguns desses dados foram analisados com a ferramenta Input analyzer (analisador de dados de entrada) do software Arena®. Segundo Prado (2010, p. 24) esta ferramenta permite analisar dados reais do funcionamento do processo e escolher a melhor distribuição estatística que se aplica a eles.

Na seção de resultados e discussão serão detalhados os dados coletados e o tratamento dado a eles visando garantir a sua consistência para utilização no modelo computacional.

2.2.1 Tamanho da amostra

O tamanho de cada uma das três amostras, cronometradas neste trabalho, foi obtida, para um nível de confiança de 95%, através da Equação (1) (Marôco, 2007).

onde: nA- número de indivíduos da amostra; Zα⁄2– valor crítico que corresponde ao grau de confiança desejado; S- desvio padrão e E- erro máximo estimado.

2.2.2 Número de replicações

O número de replicações (n*) foi obtido através da Equação 2 (Chwif; Medina, 2007).

onde: n - número de replicações já realizadas; h - semi-intervalo de confiança já obtido e h* - semi-intervalo de confiança desejado.

2.2.3 Validação do modelo

Durante a verificação e validação do modelo foi seguida a orientação metodológica proposta por Sargent (2012). Destacando, neste caso, a consistência dos dados com as pessoas familiarizadas com o processo, no caso o modelador, os funcionários da linha de esquartejamento de suínos e o funcionário responsável pela produção.

Para comparação entre os resultados reais e simulados utilizou-se, neste trabalho, o cálculo do erro médio estimado (Equação 3) (Montgomery, 2005).

onde: SE – erro médio estimado; SR – valor obtido a partir do sistema real;  MD – média dos valores gerados pelo modelo e  GLR – grau de liberdade considerando o número de replicações do modelo.

A simulação da dinâmica operacional do processo de esquartejamento foi realizada com o software ARENA®, e os resultados analisados nas ferramentas Output Analyzer e Process Analyser.

2.2.4 Outliers

Uma das principais etapas, em qualquer análise estatística de dados, é estabelecer a qualidade das observações. Atento a esse fato este trabalho utilizou a técnica de identificação de outliers (valores fora da normalidade) apresentada no Quadro 1 (Marrôco, 2007). As razões mais comuns para o surgimento desses valores são os erros na coleta de dados ou eventos raros e inesperados.

Quadro 1 – Identificação de Outliers
Fonte: Marrôco (2007)

Onde Q1 e Q3 são, respectivamente, os valores do primeiro e terceiro quartis, assim a amplitude entre inter-quartil "A" é calculada pela diferença: A=Q3-Q1.

Observa-se que neste trabalho os outliers considerados como extremos só foram descartados, das amostras, depois de uma análise criteriosa de suas causas. Os valores julgados como possíveis de ocorrer foram mantidos nas amostras.

3. Resultados e discussão

A análise dos pesos dos cortes de suínos, paleta, barriga com costela, carré com sobre paleta e pernil, e os resultados obtidos de simulação do processo de esquartejamento serão apresentados ao longo desse tópico.

3.2 Análise dos pesos dos cortes suínos obtidos

Inicialmente, avaliou-se os dados de pesos por meio de análise estatística descritiva, que de acordo com Pinheiro et al (2009) são técnicas de tratamento de dados que ajuda o pesquisador a fazer uma sondagem do terreno, tomando um primeiro contato com a informação disponível.

Os resultados dessa análise mostraram que a média de peso mais elevada encontrada foi para os cortes de pernil, 14,46 Kg, sendo que uma das peças pesou 10,88 Kg, bem menos que as demais, tendo sido considerada na plotagem do boxplot ou diagrama de caixas como um outlier (Figura 3). A seguir veio a média de peso dos carrés que foi de 11,71 Kg e não apresentou nenhum outlier.

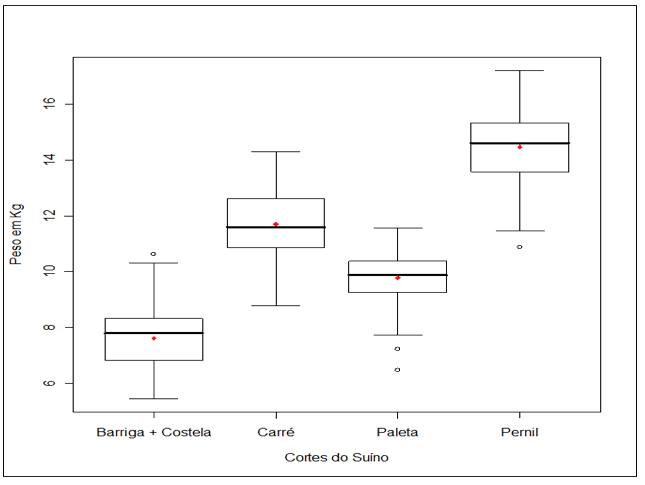
Figura 3 - Boxplots dos dados de peso coletados em 100 repetições
dos 4 tipos de cortes industrializados pela empresa estudada. Os pontos sólidos
representam as médias os pontos vazios representam os outliers
o traço central representa as medianas e os quadros apresentam os quartis.
Fonte: O autor, 2015.

Os dois produtos mais leves foram os cortes de paletas com média 9,79 Kg tendo apresentado 2 outliers de valores 7,24 Kg e 6,47 Kg e o de menor peso que foi o corte barriga com costela que apresentou uma média de peso de 7,62 Kg tendo apresentado um outlier superior de valor 10,62 Kg.

Com base nos dados apresentados na Tabela 1 percebeu-se que o valor da mediana foi inferior ao valor da média apenas para o corte de Carré com sobre paleta, o que indica uma assimetria positiva ou a direita, sendo que para os demais cortes ela mostrou-se superior ao valor encontrado para a média indicando uma assimetria negativa ou a esquerda.

Tabela 1. Resultados da estatística descritiva dos pesos dos cortes de suínos avaliados.

Dutra et al. (2001) ao avaliarem suínos abatidos com diversos pesos encontraram valores semelhantes aos encontrados neste estudo para os cortes de suínos com pesos entre 90 e 120 Kg.

Além da análise descritiva utilizou-se Gráficos de Controle Estatístico dos pesos apresentados na Figura 4. Observou-se que a maioria das médias das paletas analisadas, mantiveram-se entre a faixa de 7,28 Kg a 12,29 Kg, indicando que os cortes estão adaptados a esse padrão (Figura 4a), Dutra et al. (2001) relataram Paletas com pesos médios de 8,54 Kg e 11,70 Kg para suínos abatidos com 90 e 120 Kg respectivamente.

Notou-se que, dos 6 tipos de problemas de controle descritos por Sincish, (2006), três foram encontrados nas análises, sendo que estes foram indicados pelos números 1, 2 e 5.

O número 1 significou que existiram pontos fora dos limites de controle, nesse caso específico pesos menores que os esperados, tal fato pode ter ocorrido devido a eventualidades como um peso do animal um pouco abaixo do padrão, quando comparado às demais carcaças, ou seja suíno com menos de 90 Kg, ou o corte pode ter sido realizado de forma inadequada pelos funcionários, deixando esse corte com um tamanho menor que o recomendado.

Qualquer que tenha sido o problema pode-se observar que o percentual de ocorrência foi pequeno representando 2 % das Paletas avaliadas, mas cabe ressaltar que se faz importante avaliar as causas tendo em vista que a padronização tanto da matéria prima quanto dos cortes é de primordial importância para qualquer agroindústria.

O número 2 indicou que apareceram 7 pontos sequenciais do mesmo lado da linha central sendo que nesse caso específico estes foram notados acima da linha central indicando pesos maiores que a média para esse corte em 7 animais abatidos em sequência. O número 5 informou que 2 de 3 pontos consecutivos ficaram fora do limite de dois desvios padrão de distância da linha central, os quais nesse caso também apareceram no lado superior da linha indicando pesos superiores à média acrescida de 2 desvios padrão.

A leitura do gráfico de controle estatístico de peso das peças de Pernil indicou que todos as amostras, mantiveram-se entre a faixa de 10,53 Kg a 18,04 Kg durante todo o tempo de controle desse processo e estiveram dentro dos padrões de peso do lote de animais avaliado (Figura 4b). Dutra et al. (2001) relataram peças de Pernil com pesos médios de 11,79 Kg e 15,80 Kg para suínos abatidos com 90 e 120 Kg respectivamente.

No gráfico de controle estatístico de pesos das peças Barriga com costela observou-se que a faixa de controle ficou entre 4,57 Kg e 10,67 Kg, nesses cortes, notou-se 2 tipos de problemas de controle, sendo representados pelos números 2 e 5, indicando respectivamente 7 pontos sequenciais acima e abaixo da linha central, pois o número 2 apareceu duas vezes indicando 2 de 3 pontos consecutivos acima do limite de dois desvios padrão de distância da linha central, mas nenhuma peça ficou acima ou abaixo do limites superior e inferior de controle (Figura 4c). Dutra et al. (2001) encontraram peças de Barriga com pesos médios entre 6,17 Kg e 9,86 Kg para suínos abatidos com 90 e 120 Kg respectivamente.

A leitura do gráfico de controle estatístico de peso das peças de Carrés com Sobre Paleta, indicou que todos os cortes, mantiveram-se dentro da faixa de 7,91 Kg a 15,53 Kg, indicando assim, que os pesos, estiveram padronizados durante todo o tempo de controle do processo (Figura 4d). Dutra et al. (2001) relataram Carrés com pesos médios entre 8,66 Kg e 12,14 Kg para suínos abatidos com 90 e 120 Kg respectivamente.

Com base nos dados de pesos dos cortes dos animais abatidos pela agroindústria em comparação com os pesos médios de rendimento apresentados por Dutra et al. (2001) estima-se que os suínos que entraram para o abate durante o tempo de coleta dos pesos dos cortes possuíam entre 90 e 120 Kg e uma idade entre 140 e 170 dias, padrões indicados como adequados para o abate.

De acordo com Ellis e Bertol (2001), o aumento da idade e peso ao abate traz potenciais desvantagens pois tende a aumentar os teores de gordura na carcaça e nos cortes, além de ocasionar a redução da eficiência alimentar que ocorre quando os animais ficam mais pesados. Dessa forma existe uma preferência pelo abate de animais em uma faixa intermediária de pesos, que de acordo com os autores estaria na faixa entre 90 e 120 Kg.

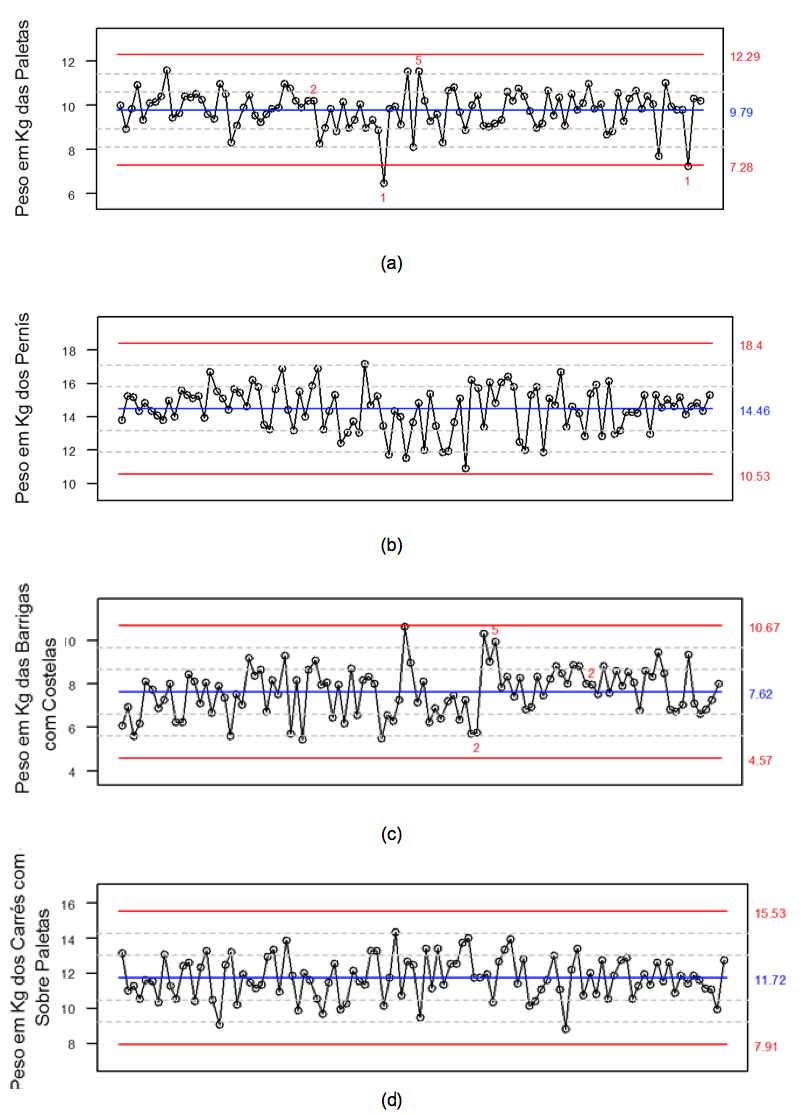
Figura 4. Gráficos de Controle Estatístico de Pesos de 100 suínos abatidos na linha de produção da Agroindústria Acompanhada.

3.1 Simulação do processo de esquartejamento

3.1.1 Tratamento dos dados

Inicialmente, realizou-se uma análise descritiva dos tempos coletados na linha de esquartejamento da empresa (Tabela 2).

Tabela 2 – Análise de dados dos tempos dos processos, coletados no
mezanino onde ocorre o processo de esquartejamento dos suínos.

   Fonte: O Autor, 2014.

A seguir, aplicou-se a técnica de identificação dos outliers nos dados coletados na linha de esquartejamento. Como pode-se observar através dos boxplots apresentados na Figura 5 não foram encontrados outliers.

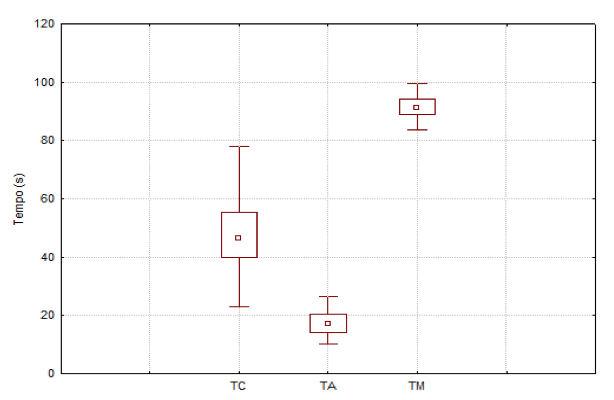
Figura 5 – Boxplots dos tempos dos processos coletados na linha.
Fonte: O Autor, (2014).

Após a análise dos dados cronometrados no sistema, através de técnicas estatísticas (MARIN; TOMI, 2010), o passo seguinte foi determinar as curvas de distribuição teórica de probabilidades que melhor representem o comportamento estocástico do sistema em estudo, através da ferramenta Input Analyzer do Arena®. Como os p-values dos testes de aderência: teste Chi Square e do teste Kolmogorov-Smirnof são maiores que o nível de significância adotado (0,1) (Chiwf; Medina, 2007), concluiu-se que as distribuições, apresentadas na Tabela 3, são as expressões que melhor se adaptaram aos dados coletados no sistema.

Tabela 3 – Distribuições de Probabilidade

    Fonte: O Autor, 2014.

3.2 Validação do modelo implementado

A validação, do modelo computacional, foi realizada por meio da técnica face a face, onde o modelo foi executado para os funcionários do setor de esquartejamento que o consideraram correto. Na sequência realizou-se uma comparação (Tabela 4), entre a média obtida do sistema real com a média gerada pelo modelo para a variável Tempo de Abate de um lote (1540) de Suínos (TAS) em um turno de trabalho. Nesta tabela apresenta-se, também, o erro médio estimado (SE, em decimal).

  Tabela 4 - Dados do sistema real e do modelo

   Fonte: O Autor, 2014.

Através da análise dos resultados da Tabela 4 pode-se concluir que o modelo computacional apresenta uma boa aproximação, em relação ao tempo de abate de um lote de 1540 suínos, em um turno de trabalho (8 horas), com o sistema real.

3.3 Simulação

Uma vez validado o modelo computacional (Figura 6), pode-se passar, segundo o método de pesquisa, para a etapa de análise. Nessa etapa o modelo computacional, agora denominado operacional, passa a trabalhar para o modelador com o intuito de responder aos objetivos do projeto de simulação.

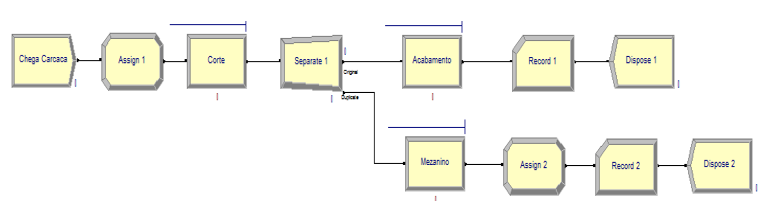
Figura 6 – Modelo computacional do Processo de Abate de Suínos
Fonte: O Autor, 2014.

Identificou-se, através de contatos com funcionários da indústria, que o gargalo do processo de esquartejamento é a ocupação dos funcionários que atuam no setor de corte da paleta, devido a velocidade da esteira (7 suínos por minuto). Atualmente trabalham 3 funcionários neste setor. Para a realização da análise da ocupação dos funcionários, são propostos sete cenários com o objetivo de observar a resposta do sistema a partir de alterações no número de suínos que chegam ao setor de corte por minuto. Os indicadores de desempenho utilizados para a análise são: o número de suínos industrializados e a utilização média dos funcionários do setor de corte da paleta. A Tabela 5 apresenta os resultados obtidos da simulação do sistema após 15 replicações, para os sete cenários.

Tabela 5 – Resultados de simulação.

Fonte: O Autor, 2014.

Observa-se dos resultados obtidos da Tabela 5, que para um lote de 1540 suínos, a velocidade da esteira de 7 suínos por minuto está dentro dos parâmetros de ocupação (85%) adotados pela empresa.

4. Conclusões

De acordo com os resultados das análises procedidas para a validação do modelo computacional, foi possível concluir que o mesmo pode ser aplicado para simular a dinâmica operacional do processo esquartejamento de suínos, principalmente na previsão da variável TAS (Tempo de Abate de um lote de Suínos). A aplicação da simulação computacional gerou um conhecimento adicional à cerca do processo para todos os envolvidos e possibilitou a afirmação de que a ocupação dos funcionários do setor de corte da paleta está dentro dos parâmetros estabelecido pela empresa.

Em relação aos resultados dos pesos dos cortes de paleta, pernil, barriga com costela e carré com sobre paleta, seguiram em sua grande maioria os recomendados pela literatura. Observou-se que existe uma certa padronização da matéria prima e que a agroindústria possui ainda um quadro de funcionários bem treinados para o processo estudado.

O controle estatístico de processos, em especial os gráficos de controle, mostraram-se muito úteis e práticos para uma obtenção de um panorama de como se encontra os pesos dos produtos estudados. A obtenção das médias e dos limites de controle possibilitou o levantamento de algumas observações pertinentes ao desempenho dos produtos e esclareceu alguns pontos importantes que devem ser estudados no setor de esquartejamento para um melhor aproveitamento na gestão da qualidade da empresa.

O levantamento dos dados deverá ser continuado para que as possíveis causas sejam levantadas em diferentes períodos e se obtenha a cultura do acompanhamento do processo na indústria. A conscientização e treinamento dos funcionários da empresa sobre a importância do controle de qualidade e de conceitos de estatística também são de relevante importância.

A implantação do controle estatístico de processo em todos os níveis da indústria de abate de suínos, permitirá liberar o tempo da gerência para os projetos de melhoria que tornarão a indústria mais competitiva.

Referencias bibliográficas

ALVES, R.; SANTOS, J. A. A.; SCHMIDT, C. A. P. Aplicação dos princípios da teoria das restrições e de técnicas de simulação na gestão da dinâmica operacional de um pequeno restaurante: um estudo de caso. Revista Espacios, v. 35, p. 21, 2014.

ALENCAR, J. R. B.; LOPES, C. E. SOUZA JR., M. B. Controle Estatístico de Processo Multivariado: aplicação ao monitoramento da produção de comprimidos de captopril. Revista Brasileira de Farmácia, v.88, n.4, p.200-205, 2007.

BAUMGARTNER, D.; CAVALLI, D.; SANTOS, J. A. A.; SCHMIDT, C. A. P. Aplicação dos princípios da teoria das restrições e de técnicas de simulação na gestão da dinâmica operacional de um pequeno restaurante: um estudo de caso. Revista Espacios, v. 34, p. 10, 2013.

CHWIF, L.; MEDINA, A. C. Modelagem e simulação de eventos discretos.

Teoria & Aplicações. São Paulo: Brazilian Books, 2007.

DUTRA, W. M. et al. Estimativas de Rendimentos de Cortes Comerciais e de Tecidos de Suínos em Diferentes Pesos de Abate pela Técnica de Ultra-sonografia em Tempo Real. Revita Brasileira de Zootecnia, v.30, n.4, p.1243-1250, 2001.

ELLIS, M.; BERTOL, T. M. Efeitos do Peso de Abate Sobre a Qualidade de Carne Suína e da Gordura. In: CONFERÊNCIA INTERNACIONAL VIRTUAL SOBRE QUALIDADE DE CARNE SUÍNA, 2, 2001. Anais....Concórdia: Embrapa Suínos e Aves, Brasil, 2001.

FERNANDES, C. A.; SILVA, C. S.; PEREIRA, J. O. YAMAGUCHI, M. M. Simulação da Dinâmica Operacional de uma Linha Industrial de Abate de Suínos. Ciência e Tecnologia de Alimentos, v. 26, p. 166-170. 2006.

IBGE. Pesquisa trimestral do abate de animais. Disponível em: <http://www.sidra.ibge.gov.br/bda/tabela/listabl.asp?c=1093&z=t&o=24>. Acesso em: 18 mai. 2015.

LIMA, U. A. Matérias primas dos Alimentos. São Paulo: Edgard Blucher, 2010. 282p.

MARIN, T.; TOMI, G. F. C. Modelagem de dados de entrada para simulação estocástica del lavra. Revista Escola de Minas, v. 60, p. 559-62. 2010.

MARRÔCO, J. Análise Estatística com Utilização do SPSS. 5 ed. Pero Pinheiro: Silabo, 2011, p.824.

MIYAGI, P. E. Introdução a Simulação Discreta. 2006. Disponível em: <http://sites.poli.usp.br/d/PMR2460/Arquivos/Apostila_Simulacao.pdf>. Acesso em 30 de out de 2013.

MONTGOMERY, D. C. Design and Analysis of Experiments. New York: Wiley, 2005.

MULTINOX - Equipamentos Agroindustriais. Mesa rolante

Para cortes de carcaças suínas. 2014. Disponível em: <http://www.multinox.ind.br/produtos/frigorificos/suinos/mesa-rolante-para-cortes-de-carcacas-de-suinos>. Acesso em 20 de janeiro de 2014.

OLIVEIRA, C. C.; GRANATO, D.; CARUSO, M. S. F.; SAKUMA, A. M. Manual para elaboração de cartas de controle para monitoramento de processos de medição quantitativo em laboratório de ensaios. São Paulo: Instituto Adolfo Lutz, 2013.

PINHEIRO, J. I. D.; CUNHA, S. B.; CARVAJAL, S. R.; GOMES, G. C.  Estatística básica: a arte de trabalhar com dados. Rio de Janeiro: Elsevier, 2009.

SINCISH, M. B. Estatística para administração e economia. 10. ed. São Paulo: Pearson Prentice Hall. 2006.

1. Email: vankli@hotmail.com

2. Email: cs910@yahoo.com.br