Espacios. Vol. 36 (Nº 13) Año 2015. Pág. 3
Abordagens heurísticas de solução para Problemas de Roteamento de Veículos (PRV)
Solution heuristic approaches for Vehicle Routing Problems (VRP)
Joaquim Rodrigo de OLIVEIRA 1; Antonio Sérgio COELHO 2
Recibido: 15/03/15 • Aprobado: 02/05/2015
Contenido
3. Formulação do modelo matemático do problema geral de roteamento de veículos (PRV)
4. Estratégias para a solução dos problemas de roteamento de veículos (PRV)
5. Abordagen heurística da solução
10. Referências bibliográficas
RESUMO: |
ABSTRACT: |
1. Introdução
A importância e a influência do modo de formular um problema de otimização, especialmente em áreas complexas como a de roteamento de veículos, busca-se entendimento, sendo evidente que a formulação terá impacto direto no desempenho dos algoritmos de solução. Para Goldbarg & Luna (2005) esse fato não é apenas intuitivo, ele possui justificativas teóricas, é fácil perceber que existirá uma relação entre o tamanho do espaço das soluções viáveis de um problema, bem como suas características, com a possibilidade de obtermos bons algoritmos de solução para o caso.
Para Hiller (2006), essa abordagem nem sempre funciona. Alguns problemas são tão complicados que pode ser que não seja possível encontrar uma solução ótima. Em tais situações, ainda é importante encontrar uma solução viável que seja próxima a solução ótima, as heurísticas são usadas em busca de tal solução.
Segundo Goldbarg & Luna (2005) é ponto pacífico que, quanto maior for o número de variáveis de restrições de um mesmo problema, normalmente maior será o esforço necessário para encontrarmos a solução.A Característica do espaço de solução é outro ponto fundamental, sendo a integração um fator conhecidamente complicador. Como a formulação de um problema pode interferir fortemente em seu processo de solução, o estudo das possíveis alternativas de formulação utilizando heurísticas, é um tema relevante.
As heurísticas construtivas devem apresentar estratégias para construir uma solução viável, próxima da ótima para o problema. O Objetivo do estudo se concentra na aplicação de abordagens heurísticas na resolução de problemas de roteamento de veículos (PRV).
2. Definindo heurística
Não é difícil imaginar a importância e significado de uma atividade produtiva e criadora. Descobertas científicas, criação de novas formas de construção, formulação e resolução de problemas complexos. Nem de longe compõe a relação dos diversos trabalhos em que, como importantíssimo componente, entra a atividade criadora, esse componente comprova até que ponto são relevante estudos dessa atividade e a descoberta de sua constante.
Heurística é a ciência que estuda as constantes da atividade do pensamento criador. Seus objetivos não se reduzem apenas às pesquisas das constantes do pensamento criador, mas compreendem também a elaboração de métodos e modos de direção dos processos heurísticos, sendo também ao âmbito da heurística os trabalhos experimentais, através dos quais cientistas cibernéticos procuram dar forma às manifestações superiores do intelecto humano. (PUCHKIN 1969 p. 8)
Segundo Ferreira (2011) a heurística é uma técnica que busca boas soluções ótimas e sub ótimas a um custo computacional razoável, sem garantia de otimalidade ou factibilidade sendo em muitos casos, incapaz de declarar quão próxima uma solução factível está da solução ótima.
A noção da atividade heurística é algo mais restrito do que a do pensamento, sendo predominante na atividade mental humana, diversas operações intelectuais elaboradas durante a aprendizagem e o desenvolvimento, bem como imagens intelectuais e automatismos.
Um dos mais importantes matemático do século XX o francês Jules Henri Poincaré, nos deu uma das mais expressivas descrições da atividade heurística. Ao narrar no seu primeiro trabalho (Memórias sobre as Funções de Fuchs), e nos revela algumas peculiaridades dessa atividade.
Durante duas semanas, Poincaré procurou comprovar a inexistência de quaisquer outras funções idênticas àquelas a que posteriormente denominou funções de Fuchs. Punha-se diariamente à mesa de trabalho, aí permanecendo, de uma a duas horas, a examinar uma série infinita de combinações, sem, todavia, chegar a uma conclusão. "certa feita, à noite, escreve Poincaré", "por ter tomado, contra meus hábitos, uma pequena xícara de café, não pude dormir. As idéias atormentavam-me o cérebro. Sentia como se estivesse havendo um choque entre elas. Até que, afinal, poder-se-ia até dizer, duas delas se uniram, formando uma combinação aceitável". Pela manhã, parte do problema estava resolvido. Restava-lhe somente formular as conclusões, o que não exigiu mais do que poucas horas (PUCHKIN, 1969, p.9).
Segundo Palavras de Poincaré [3], as tentativas de solucionar o problema apenas levam à verificação do grau de sua complexidade.
Puchkin (1969), comenta que ainda no século XVII, os filósofos racionalistas Descartes, Spinoza e Leibnitz prepararam alguns importantes componentes do pensamento criador. As teses desses filósofos, no que tange à intuição, revelam-se interessantes para a apreensão da específica atividade heurística. Eles mostram que na composição de atividade intelectual humana existem verdades que são descobertas pelo intelecto não à base de argumentação lógica e raciocínio, mas através de uma peculiar e súbita "visão intelectual"
3. Formulação do modelo matemático do problema geral de roteamento de veículos (PRV)
Para entender os problemas de roteamento de veículos (PRV) faz-se necessária uma definição sobre problema de de roteamento e os sistemas de roteamento. Novaes (2004) define um problema de roteamento sendo três fatores fundamentais: decisões, objetivos e restrições. Como objetivos principais, o processo de roteirização visa propiciar um serviço de alto nível aos clientes mas ao mesmo tempo mantendo os custos operacionais e de capital tão baixo quanto possível.
Goldbarg e Luna (2005) consideram um sistema de roteamento um conjunto organizado de meios com o objetivo de atender pontos de demanda localizados em arcos ou vértices de alguma rede de transportes. As decisões estratégicas afetam todo o sistema e possuem efeito duradouro, podendo tornar menos claras com o aumento da complexidade e do tamanho dos sistemas.
Para Ferreira (2011) em linhas gerais os Problemas Roteamento de Veículos (PRV), se resumem à definição de rotas para atendimento de demandas, as quais podem se apresentar na forma tanto de prestação de serviço como na coleta e/ou entrega de pessoas ou mercadorias em uma determinada região geográfica.
O objetivo é criar rotas para que os veículos possam transportar as demandas, sempre respeitando uma série de restrições operacionais e minimizando os custos envolvidos. Cada rota se da início em um depósito e termina no mesmo, sendo cíclico. Esse tipo de problema aparece em um grande número de situações. Pode citar atividades como:
- entrega, em domicílio, de produtos comprados nas lohas de varejo ou pela internet;
- distribuição de bebidas em bares e restaurantes;
- distribuição de dinheiro para caixas eletrônicos em bancos;
- coleta de lixo urbano etc.
Para o desenvolvimento de formulações do problema de roteamento de veículos (PRV) e quando nada for observado em contrário, Goldbar e Luna (2005) consideram o seguinte:
- O grafo de substrato não direcionado G = (N,A)
- S* = N \ S para S C= N
Uma das formulações matemática mais utilizadas para o problema de rotemaento de veículos tem como base a diversos métodos de solução é a de Fisher e Jaikumar (1981, apud GOLDBAR & LUNA, 2005)
Formulação do Problema Geral de Roteamento

Sujeito a:
![]()
![]()
![]()
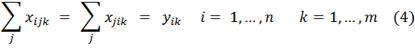

![]()
![]()
Onde:
xijk ≡ variável binária que assume o valor 1 quando o veículo kvisita o cliente j imediatamente após o cliente i, 0 em caso contrário.
yik ≡ variável binária que assume valor 1 se o cliente i é visitado pelo veículo k, 0 em caso contrário.
qi é a demanda do cliente i.
Qk é a capacidade do veículo k.
cij é o custo de percorrer o trecho que vai do cliente i ao j.
As restrições (1) asseguram que um veículo não visite mais de uma vez um cliente. As restrições (2) garante que o depósito recebe uma visita de todos os veículos. As restrições (3) obrigam que a capacidade dos veículos não seja ultrapassada. As restrições (4) garantem que os veículos não param suas rotas em um cliente. As restrições (5) são as tradicionais restrições de eliminação de sobtours.
4. Estratégias para a solução dos problemas de roteamento de veículos (PRV)
4.1 Classificação dos problemas
Os problemas de roteamento de veículos variam quanto a sua complexidade dependendo do número de variáveis e restrições que o problema considera em sua formulação. Alguns problemas podem ser considerados quanto a sua complexidade como intratáveis.
Para Goldbar e Luna (2005) os problemas em que as variáveis assumem valores inteiros ou que possuem funções objetivo com descontinuidades não podem, geralmente, ser solucionados diretamente pelo algoritmo simplex. Esse é o caso de grande parte dos problemas ditos de roteamento. Para esses problemas complexos, a otimização utiliza técnicas para alcançar soluções próximas da ótima, como as heurísticas. A Figura 1, abaixo, mostra como a pesquisa operacional desenvolveu estratégias para tratar cada tipo de problema.

Figura 1 – Estratégias para solução de PRV. (GOLDBARG & LUNA, 2005)
5. Abordagen heurística da solução
Os problemas de roteamento de veículos (PRV) são de grande complexidade sendo assim o nosso foco se concentra na abordagem heurística. Vamos destacar algumas abordagens em nosso estudo, para que se entenda a sua utilização na resolução desses problemas.
5.1 Heurísticas construtivas
Há várias abordagens heurísticas para resolver um Problema de Roteamento de Veículos. Novaes (2004) agrupa essas abordagens em duas categorias: métodos de construção de roteiros e métodos de melhoria de roteiros. Nosso estudo será focado na resolução de problemas de roteamento utilizando a abordagens de heurísticas construtivas que Goldbarg e Luna (2005) descrevem a seguir:
5.1.1 Procedimento de Economia e Inserção
Essas abordagens constroem uma solução através de um conjunto de configurações que a cada passo é atualizado. Os algoritmos realizam a progressão de uma configuração para outra segundo critério de minimização da função objetivo, também chamado de saving ou economia. Um trabalho clássico dentro dessa linha de atuação é o de Clark e Wright (1964, apud GOLDBAR & LUNA, 2005)
Heurística de Clark e Wright
Considerando que o vetor sij represente o valor da economia obtida pela reorganização de duas ligações do tipo (i - 1 - i) e (j -1 – j) em uma nova (i, j) como mostra a figura 2
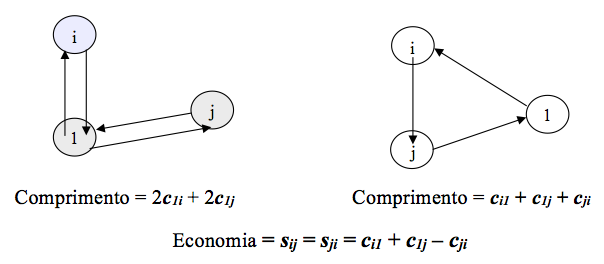
Figura 2 – O Procedimento de Economia (GOLDBARG & LUNA, 2005)
De um modo geral o algoritmo procede da seguinte forma:
Algoritmo Clarck e Wright (sequencial) |
INÍCIO Ler G = (N,A), cij . {*nó 1 é o depósito central do roteamento*} Inicializar Rota := (x1 – xs – x1), Calcular a economia sij := c1j – cij + cj1 para todo o par de clientes xi e xj {*nós em G*} Ordenar as economias em ordem não crescente e colocá-las em uma lista Enquanto existir ligações na lista Faça Iniciando pela maior economia da lista Faça Início Determine a primeira ligação na lista que pode ser utilizada para ser acrescida em um dos dois extremos da Rota, aumentando o seu comprimento e a retirando da lista; Se Rota não pode ser expandida da forma anterior então escolha a primeira ligação na lista para iniciar uma nova rota, e a retire da lista Fim FIM |
Estratégia de solução da aplicação da Heurística de Clark e Wright:
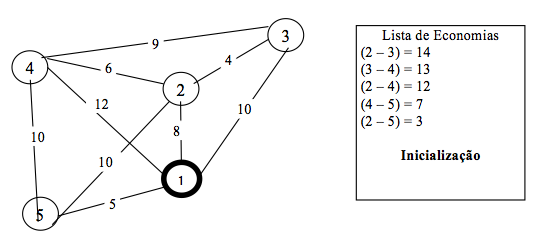
Figura 3 – Lista de economias – Inicialização (GOLDBARG & LUNA, 2005)
-----

Figura 4 – Lista de economias – 1ª melhoria (GOLDBARG & LUNA, 2005)
-----
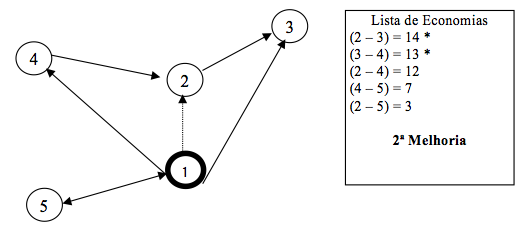
Na medida em que uma rota vai sendo construída é possível realizar os testes relativos a restrições de capacidade de veículos e, eventualmente, de janelas de tempo. Em relação ao comportamento do algoritmo ele possui a característica de aninhar os clientes nas rotas que vão se formando. Notamos que o nó 3, após a segunda melhoria, passou à condição de interno (sem ligação direta com o vértice depósito) não sendo mais candidato a melhoria na rota, uma vez que só são testados para a inserção os nós extremos ou seja, aqueles que se ligam diretamente ao nó central (vértice 1).
-
Heurística de Mole e Jamenson
Mole e Jamenson (1976, apud GOLDBARG & LUNA, 2005) descreve a abordagem sendo que o algoritmo ataca a fragilidade dos nós internos não serem candidatos a fazer parte do teste de economia, permitindo que a inserção de economia possa ser realizada entre dois nós intermediários. O critério para expandir a rota pela inclusão de novos vértices no algoritmo tem duas condições.
- e (i, l, j) = cie + cij – μcij
- σ(i, l, j) = λc0l – e(i, l, j)
De um modo geral o algoritmo procede da seguinte forma:
Algoritmo Mole e Jamenson |
INÍCIO Ler G = (N,A), cij . {*nó 1 é o depósito central do roteamento*} Inicializar F:= N \ {x1} Enquanto F # 0 Faça Início Rota := {x1 – xs – x1} {*vários critérios podem ser utilizados nesta atribuição*} Para todos os vértices x1 E a F Início verifique uma possível inserção na rota em exame que atenda a : e(i1, l, j1) = min[e(i, l, j)] e considere todos os vértices vizinhos xr e xs E Rota onde xj1 são os vértices entre os quais x1 será incluido e que representem a "melhor escolha" (Procedimento MV); Fim Inserir o vértice na rota corrente entre os vértices xi1 e xj1 e fazer F:=\{x1*} Otimizar a rota R utilizando métodos r-ótimos2 Fim FIM |
(*) Procedimento MV (Melhor Vértice)
INÍCIO Para todos os nós x1 ainda não incluídos na rota R e viáveis, o "melhor vértice" x1* a ser inserido é o que (il*, l*, jl*) = max[σ (ii, l, jl)] FIM |
Exemplo numérico do procedimento de Mole e Jameson, a heurística possui dois parâmetros de controle que podem ser modificados em conformidade com os desejos e estratégia da solução.
- λ = 0 e μ = 1 → a inserção será realizada levando em conta a minimização do aumento da rota pela inclusão de um novo cliente.
- λ = 0 e μ = 0 → a inserção será realizada levando em conta a minimização da distância entre os dois vizinhos.
o caso em que 1 ≤ λ ≤ 2; μ = λ – 1 trata-se de uma generalização do critério de Gaskell (1976, apud GOLDBARG & LUNA, 2005).
λ → ∞, 0 < μ < ∞ → a inserção ocorrerá para o cliente mais distante do depósito.
Se λ cresce, o peso para a distância entre o cliente e o depósito cresce, levando à formação de rotas mais circulares. Quando μ cresce as ligações mais longas são penalizadas.
Estratégia de solução de aplicação da Heurística de Mole e Jamenson:
Considerando λ = 1 e μ = 1 e o grafo da figura 6 e considerando a rota parcial do grafo da figura 7 em que os nós fora da rota são 4 e 6.
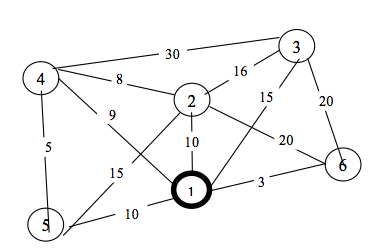
Figura 6 – Rede de Roteamento (a) (GOLDBARG & LUNA, 2005)
-----

Figura 7 – Rota Parcial (b) (GOLDBARG & LUNA, 2005)
-----
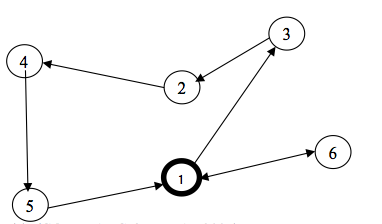
Figura 8 – Inserção (c) (GOLDBARG & LUNA, 2005)
Para realizar uma inserção o algoritmo calcula inicialmente uma lista de proximidades da seguinte forma:
l = 4 |
l = 6 |
e(2, 4, 5) = 13 e(5, 4, 1) = 14 e(3, 4, 2) = 38
|
e(2, 6, 3) = 40 |
Como exemplo, e(2, 4, 5) = 8 + 5 = 13. Sendo o nó 4 escolhido para inserção (mais próximo dos vizinhos). Para realizar a inserção o critério da função σ é utilizado conforme a tabela abaixo
Inserção Entre |
l = 6 |
2-5 1-5 2-3 |
σ (2, 4, 5) = 20 σ (3, 3, 2) = 20 |
Como exemplo, σ(2, 4, 5) = 18 + 15 – 13 = 20. O que resulta na inserção que a figura 8 mostra com que economia de 20 unidades para rota anterior.
5.1.2 Procedimento de Primeiro Agrupar e Depois Rotear
GOLDBARG e Luna (2005) definem essa estratégia sendo a procura de obtenção da solução em duas etapas distintas. A primeira visa agrupar os pontos de demanda segundo algum critério de proximidades, enquanto que na segunda etapa cada grupo (ou cluster)é selecionado independentemente.
Um exemplo dessa abordagem heurística pode ser encontrado no trabalho de Gillet e Miller (1974, apud GOLDBARG & LUNA, 2005), onde a estratégia parte do princípio que os trajetos entre nós serão desenvolvidos preferencialmente entre vizinhos. No quadro que se segue foi desenvolvido uma versão heurística que permite evidenciar sua enorme eficiência e simplicidade na fase de agrupamento.
De um modo geral o algoritmo procede da seguinte forma:
Algoritmo Gillet e Miller |
INÍCIO Ler G = (N,A), cij . {*nó 1 é o depósito central do roteamento*} Obter as coordenadas polares dos clientes em relação ao depósito e ordená-las em ordem de crescimento de seu valor e Fazer: Início F: = N \ {x1} Ponta_Rota = {x1} Rota1 := {x1 } i := x1 Fim Enquanto F # 0 Faça {*Agrupar*} Início Enquanto ∃ xs ∈ F atendendo às condições de viabilidade para Rotai Encontrar o vértice xs ∈ F de coordenada polar mais próxima de Ponta_Rota e Fazer Início Rotai ::= Rotai ∪ {xs} Ponta_Rota = {xs} F := F \ {xs} j := j + 1; Se controle(j) = Verdadeiro então aplicar Procedimento k-ótimo ( Rotai) Fim Fim Início i := i + j Ponta_Rota := {x1} Rotai := {x1} Fim FIM |
Estratégia de solução de aplicação da Heurística de Gillet e Miller:
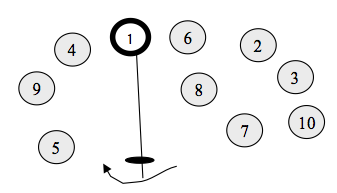
Figura 9 – Procedimento de Agrupar (a) (GOLDBARG & LUNA, 2005)
-----
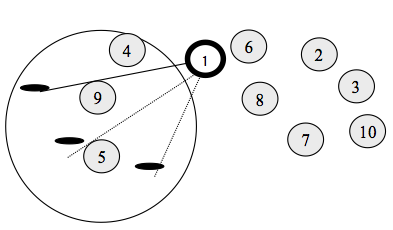
Figura 10 – Grupamento em Formação - Varredura (b) (GOLDBARG & LUNA, 2005)
-----

Figura 11 – Formato Inicial das Rotas (c) (GOLDBARG & LUNA, 2005)
As figuras 9,10 e 11 exemplificam a aplicação da abordagem heurística de Gillet e Miller ao grafo da figura 9. A varredura se desenvolve a partir do vértice 5 e no sentido horário.
6. Metodologia da pesquisa
O desenvolvimento do trabalho envolveu várias áreas do conhecimento. Nestas diversas áreas, os devidos aprofundamentos foram feitos gradativamente. As etapas do trabalho e implementação do sistema foram:
- pesquisa sobre Pesquisa Operacional (PO) e suas aplicações;
- pesquisa sobre Heurísticas, Métodos Heurísticos e sua importância na atualidade, bem como aplicações e sugestões de estudos na área;
- pesquisa sobre Problemas de Roteamento de Veículos (PRV) e suas aplicações;
- pesquisa sobre a formulação do modelo matemático do Problemas de Roteamento de Veículos (PRV);
- análise de cenários para aplicação de estratégias de abordagens heurísticas na solução.
7. Modelagem do problema
Dado um conjunto de cidades (ou consumidores), cada qual com uma demanda qipor um produto, e um depósito com veículos de capacidade Qk, como encontrar as rotas para os veículos minimizando os custos de transporte, aplicando abordagens Heurísticas?
8. Trabalhos futuros
Segundo Novaes (2004) existe no mercado um número razoável de softwares de roteirização, que ajudam as empresas a planejarem e programarem os serviços de distribuição física. Sendo assim é relevante a criação de um software heurístico parametrizado que vai possibilitar em um ambiente computacional a otimização e resolução de Problemas de Roteamento de Veículos (PRV)
Aplicação da Roteirização Probabilística que Novaes (2004) define sendo o estabelecimento de visitas num roteiro, não são fixas, pois nem sempre os clientes emitem pedidos de forma regular. Esse tipo de roteirização aparece com bastante freqüência na distribuição das compras no comércio eletrônico, pois o conjunto de clientes a ser visitado varia dia a dia, sendo recomendada a alocação de um roteiro básico de referência. Sendo assim é relevante a aplicação de métodos heurísticos para resolução de problemas de roteamento.
9. Considerações finais
Os Problemas de Roteamento de Veículos (PRV), são muito estudados e analisados, principalmente pela sua grande aplicabilidade nas áreas de Logística e Supply Chain Management. Porém, mesmo possuindo uma formulação exata relativamente simples, sua resolução analítica é de alta complexidade. Tal contexto propicia a utilização de heurísticas como instrumentos fundamentais de resolução destes problemas, conforme demonstrado neste trabalho. O presente estudo buscou um entendimento de três abordagens heurística baseada nas estratégias: procedimentos de economia e inserção e procedimentos de primeiro agrupar e depois rotear. Analisou-se as abordagens apresentadas e pode-se concluir que as mesmas são de grande importância na resolução de problemas complexos de roteamento.
10. Referências bibliográficas
DANTZIG, G., RAMSER, J., (1959). The truck dispatching Problem. Management Science, 6:81-691.
FERREIRA, Vanessa de Oliveira. Uma abordagem heurística para o problema de roteamento de veículos com designação de entregadores extras. São Carlos : UFScar, 2011. 92 p.
GOLDBARG, Marco César; LUNA, Henrique Pacca L. Otimização combinatória e programação linear: modelos e algoritmos. 2.ed.rev. e atual. Rio de Janeiro: Campus, 2005.
GONÇALVES, S. M. Uma Metodologia para o Roteamento de Veículos – o Estudo de Caso da Distribuição de Água Mineral em Itú, São Paulo. Curitiba, 2003. Dissertação (Mestrado em Métodos Numéricos em Engenharia) - Universidade Federal do Paraná.
HILLIER, Frederick S. Introdução à pesquisa operacional. 8.ed. São Paulo : McGRAW-HILL, 2006.
NOVAES, Antônio Galvão. Logística e gerenciamento da cadeia de distribuição: estratégia, operação e avaliação. Campinas: Campus, 2004.
POINCARÉ, J. H., A Criação da Matemática, 1909
PUCHKIN, V. N. Heurística: a ciência do pensamento criador. Rio de Janeiro: Zahars, 1969. 181 p.
REEVES, C. R. Modern heuristic technicques for combinatorial problems. John Wiley & Sons. Inc. New York, 1993.
1. Doutorando em Engenharia da produção e Sistemas . UFSC- Universidade Federal de Santa Catarina Professor Centro Universitário UNIFACVEST-Lages/SC profrodrigo@globo.com
2. Professor associado II na UFSC- Universidade Federal de Santa Catarina a.s.coelho@ufsc.br
3. Poincaré J. H., A Criação da Matemática, 1909.