Espacios. Vol. 36 (Nº 10) Año 2015. Pág. 15
Previsão para o volume de vendas no varejo - Combustíveis e lubrificantes - no estado do Rio Grande do Sul
Study of a model to forecast the volume of retail sales - Fuels and lubricants in the state of Rio Grande do Sul
Claudia Aline de Souza RAMSER 1, Adriano Mendonça de SOUZA 2, Tatiana Fernanda MOUSQUER, Luciana ROCKENBACH de Moares, Antonio Vanderlei dos SANTOS, Adenise CLERECI, Jeferson Pinto de MORAES, Maria Aparecida Brum TRINDADE.
Recibido: 08/02/15 • Aprobado: 22/02/2015
Contenido
RESUMO: |
ABSTRACT: |
1. Introdução
O petróleo é a matéria prima utilizada para gerar a gasolina, óleo diesel e seus derivados, todos estes produtos servem de combustível para máquinas e automóveis, sabe-se que vários produtos são derivados do petróleo, exemplo, a parafina, gás natural, GLP, produtos asfálticos, nafta petroquímica, querosene, solventes, óleos combustíveis, óleos lubrificantes, óleo diesel e combustível de aviação. (GURGEL, NETO, s/a, p 25).
Somente no ano de 1939 no Brasil foi descoberto o óleo de Lobato na Bahia. Depois de alguns anos a Petrobras foi criada, em 1954, com o objetivo de monopolizar a exploração do petróleo no Brasil, com isto, muitos poços foram perfurados. Atualmente, a Petrobras está entre as maiores empresas petrolífera do mundo. Estando presente em 27 países. Em 2007, a Petrobras foi classificada como a 7ª maior empresa de petróleo do mundo com ações negociadas em bolsas de valores, de acordo com a Petroleum Intelligence Weekly (PIW), publicação que divulga anualmente o ranking das 50 maiores e mais importantes empresas de petróleo. O petróleo é uma das principais commodities minerais produzidas pelo Brasil.
Sabe-se que o Brasil a partir do ano 2006 se tornou um país auto-suficiente na produção de petróleo. A Agência Nacional de Petróleo, Gás Natural e Biocombustível(ANP, 2012), conceitua óleo diesel como produto oleoso mais abundante obtido a partir da refina do petróleo. Sua composição apresenta basicamente hidrocarbonetos (compostos orgânicos que constituem átomos de carbono e hidrogênio) e em baixas concentrações de enxofre, nitrogênio e oxigênio. É um produto inflamável, com nível médio de toxicidade, pouco volátil, sem matéria em suspensão, límpido com cheiro forte e característico. O Álcool é um combustível alternativo, tendo como matéria prima: cereais e vegetais (glicose, amido, celulose,etc) sendo obtido por fermentação anaeróbica, é um bicombustível renovável, menor emissão de poluente com seu consumo. A gasolina é o carburante atualmente utilizado nos carros, sendo uma mistura de compostos orgânicos que contém átomos de carbono e hidrogênio obtidos do petróleo bruto, por intermédio de vários processos, destilação e outros. (ANP, 2012)
Conforme informações disponibilizadas pela Secretaria de Planejamento, Gestão e Participação Cidadã do Rio Grande do Sul (SEPLAG):
A Refinaria Alberto Pasqualini - REFAP em Canoas e a Refinaria Riograndense em Rio Grande, são as responsáveis pelo total do refino do petróleo no Rio Grande do Sul. Em 2011, ambas processavam 165.147 barris/dia, o que correspondia a 8,8% da capacidade nominal nacional. Os principais derivados extraídos são: óleo diesel, óleo combustível, gasolina, gasolina de aviação, gás liquefeito de petróleo - GLP e querosene. (CARGNIN et al, s/a, s/p).
O maior gasto com combustíveis derivados do petróleo, com exceção do óleo diesel, acontece nos principais centros urbanos do Estado onde é utilizada a maior parte da frota de veículos. O consumo de óleo diesel distribui-se mais uniformemente pelos municípios, sobretudo, a sua utilização nas atividades rurais, com destaque para a lavoura arrozeira.
Conforme informações coletadas em diversos níveis de agrupamento das informações geográficas foi demonstrado pelos autores Cargninetal (s/a) mapas do uso de combustíveis no RS.
Figura 1: Consumo de gás liquefeito no ano de 2011.

Fonte: Cargninet al (s/a)
Conforme figura 1 Porto Alegre é o maior consumidor de gás liquefeito, segundo informações da Petrobras esta cidade possui gasodutos Uruguaiana-Porto Alegre de utilização limitada, fornecendo para clientes específicos.
Figura 2: Consumo de gasolina no ano de 2011.
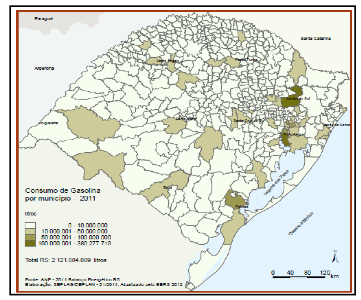
Fonte: Cargninet al (s/a)
O mapa acima descreve o consumo de gasolina no Rio Grande do Sul, sabe-se que 60% deste combustível são utilizados em carros de passeios, Porto Alegre e Caxias do sul são as cidades que mais consomem gasolina, pois esta ligada aos grandes centro de industrias e comércio.
Figura 3: Consumo de óleo diesel 2011.
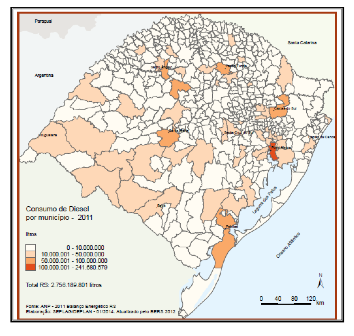
Fonte: Cargninet al (s/a)
O óleo diesel segundo Petrobras é um produto consumido por três grandes setores: o de transportes, representando mais de 75% do total consumido; o agropecuário, representado cerca de 16% do consumo; e o de transformação, que utiliza o produto na geração de energia elétrica e corresponde à cerca de 5% do consumo total de diesel.
Nota-se analisando os mapas acima que as figura 1, 2 e 3, demonstraram as regiões onde se concentra o maior consumo de combustíveis, onde a cidade de Porto Alegre é a que se destaca maior consumo em todos os tipos de combustíveis.
O objetivo deste estudo é demonstrar o consumo de combustíveis e seus derivados no estado do Rio Grande do Sul e o modelo que conseguiu capturar sua sazonalidade foi o SARIMA, e assim também demonstramos a importância desta pesquisa, pois o petróleo é um recurso natural não-renovável.
Sabe-se que outros autores estudaram a trajetória do preço dos combustíveis, como exemplo no trabalho de Almeida et al (2013), que utilizaram no trabalho o modelo auto-regressivo integrado de médias móveis ARIMA. Estes autores tiveram como objetivo realizar a previsão para o preço recebido pelo consumidor dos combustíveis (Gasolina, Álcool e Gás natural) através da modelo ARIMA, apresentando uma possível trajetória acerca do desempenho preditivo do nível de preços destes produtos em Pernambuco.
2. Material e métodos
2.1 Conjunto de dados
O conjunto de dados utilizado neste trabalho provém do site do IBGEe refere-se a uma série mensal de venda mensal (em litros) de combustíveis e lubrificantes no período de janeiro de 2000 até dezembro de 2014.
2.2 Método
Conforme abordagem de Morettin e Toloi, (2004), uma série temporal (ST) é um conjunto de observações ordenadas no tempo, que devido a essa ordenação cronológica, surge o efeito da autocorrelação entre as observações. Esta amostragem devem ser colhidas em intervalos de tempo iguais.
A ST (Zt) pode ser discreta, contínua, univariada, ou multivariada e o tempo (T) identificado como unidimensional ou multidimensional.
A análise de séries temporais apresenta como objetivo principal, a realização de previsões futuras, adotando por base seus valores presentes e/ou passados, por meio da correlação temporal que existe geralmente entre os valores exibidos pela série.
Recomenda-se a utilização de ST estacionárias, pois só assim tornam-se os efeitos sazonais aditivos e a variância residual constante garantindo a ergodicidade (representatividade) do processo. (SOUZA, s/a, s/p).
De acordo com Morettin e Toloi, (2004), a série a ser estudada deve ser estacionária, isto quer dizer, a série deve se distribuir aleatoriamente em torno de uma média constante, admitindo certa estabilidade ao longo do tempo. Dessa forma, garante-se que os parâmetros estimados para essa série sejam válidos, e confiáveis.
Para auxiliar os estudos e análises das séries temporais George Box e Gwilyn Jenkins em 1976 desenvolveram um método de análise de séries temporais que se tornou mundialmente conhecido como metodologia de Box &Jenkins, sendo que a previsão é um dos principais fatores da popularidade deste modelo. (Souza et al., 2011).
Conforme Bueno (2008), para distinguir os possíveis modelos devemos analizar a função da autocorrelação (FAC) e a função de autocorrelação parcial (PACF). Conforme tabela 1.
Tabela 1- Identificação dos modelos AR(p) e MA(q).

A tabela acima explica como se identifica o modelo por meio da função de autocorrelação (FAC) e função de autocorrelação parcial (FACP).
Um processo aleatório linear simples é o processo autoregressivo AR(p) em que p = 1. O modelo AR(p) correspondente ao processo autoregressivo de 1ª ordem ou 2ª ordem.
O modelo autoregressivo genérico AR(p) escreve-se:

Na verdade, como o nome indica, AR(p) modela uma autoregressão da variável Yt com essa mesma variável, defasada (Y t-1, Y t-2, ... , Y t-p), para os "p" períodos de defasagem em que a autocorrelação parcial entre as variáveis é significativa. Onde o p indica a ordem do modelo, ou o número de defasagens.
Já o MA(q) quer dizer modelo de médias móveis de ordem "q" significa que o Zt é uma função soma algébrica ponderada dos at, que se movem no tempo, Zt não é média, visto que os parâmetros θ ' s não somam, obrigatoriamente, a unidade. No modelo MA (q) onde "q" determina a ordem do modelo e θ é um parâmetro. (SOUZA, 2006).
2.2.1 Arma
O modelo ARMA (p,q) é formado por uma parte autoregressivo e a outra de médias móveis, onde o modelo se encontra estacionário. Podendo ser chamado método de previsão de mínimos quadrados.
2.2.2 Arima
O modelo ARIMA gera da combinação de três componentes Autoregressivo (AR), o componente de Integração (I) e o componente médias móveis (MA). Este modelo não é estacionário.
A metodologia de (Box- Jenkins, 1970) determina em ajustar os modelos ARIMA (p,d,q) a um conjunto de observações em um determinado período, onde p é a parte autoregressiva, d o número de diferenças aplicados na série para deixá-la estacionária e q é a parte de médias móveis.
Já o modelo SARIMA é um processo sazonal autoregressivo integrado de média móvel de ordem (p,d,q) X (P,D,Q)S denotado por SARIMA (p,d,q) X (P,D,Q)S onde d é a diferenciação e o D é o grau de diferenciação sazonal.
A tática usada para construção do modelo será feita por meio de um ciclo interativo conforme descrito abaixo seguindo a metodologia Box e Jenkins (1970):
Identificação, estimação, verificação e previsão. Com a identificação saberemos se a série é estacionária ou não-estacionária, para confirmar a estacionariedade usaremos os testes Dick-Fuller (ADF) e KPSS. A identificação do modelo será feita pela análise da função de autocorrelação (FAC) e função de autocorrelação parcial (FACP). A estimação será analisada pelo AIC e BIC. A adequação do modelo será feita através dos resíduos conforme Amaro e Souza (2014) que deverão ser ruído branco, ou seja, possuir média zero, variância constante e ser não correlacionado.Com a verificação saberemos qual o melhor modelo será usado para por fim fazer a previsão.
3. Resultado
Para analisar o comportamento da Série do Índice de volume de vendas no varejo - Combustíveis e lubrificantes - Rio Grande do Sul, de janeiro de 2000 a dezembro de 2014, no Rio Grande do Sul, desenvolveu-se um Gráfico da Série Original, que possibilitou observar o comportamento ao longo do período de análise.
Na figura 2, é possível observar que as Séries não assumem um comportamento estacionário por apresentar uma tendência crescente e picos, até o ponto 4 a série é estável, depois decai ate 05 e depois começa a crescer; Também observa a sazonalidade espera-se que tudo isso se reflita no modelo. Como a análise visual não é comprobatória recorreu-se aos testes Dick-Fuller (ADF) e KPSS, através da análise das Funções de Autocorrelação de cada Série Original, e aos testes de significância, para se concluir se as Séries apresentam tendência.
Figura 4: Verificação de estacionariedade.

Na figura 4 visualmente identificamos que a série não é estacionária, portanto devemos aplicar uma diferença, mas para confirmarmos esta não estacionáriedade fizemos o teste de estacionariedade Kwaiatkowski, Phillips, Schmidt and Shin (KPSS), e oTeste da raiz unitária Augmented Dickey-Fuller (ADF).
Figura 5: Paralelo do gráfico da verificação de estacionariedade, com aplicação da diferença.

Após aplicada esta diferença podemos observar na figura 3 em paralelo com o gráfico da série sem a diferença, que a série ficou estacionária, mas para confirmação aplicaremos os testes ADF e KPSS, para assim comprovar que a série se tornou estacionaria.
Tabela 2- Teste da raiz unitária Augmented Dickey-Fuller (ADF)

H0 =p = 0 não estacionária
H1 = p≠ 0 é estacionária
Tabela 3- Teste de estacionariedadeKwaiatkowski, Phillips, Schmidt andShin (KPSS).

H0 =p = 0 é estacionária
H1 = p≠ 0 não estacionária
Analisada a estacionariedade da série, conclui-se que ela torna-se estacionária, após a primeira diferença, o próximo passo é identificação dos modelos significativos que representam o comportamento do preço das vendas no varejo de combustíveis e derivados.
Através da estimação de vários modelos(tabela 4), observou-se os modelos significativos encontrados bem como seus parâmetros. Onde o modelo que foi capaz de capturar a sazonalidade da série, revelando os períodos de maior e menor consumo.
Tabela 4- Modelos

Como regra de decisão para optar pelo melhor modelo, usou os Critérios o AIC e o BIC, que definem os modelos parcimoniosos, por meio dos menores valores encontrados. Tais valores encontram-se na tabela 4. Encontrados os modelos significativos, o próximo procedimento é a verificação das Funções de Autocorrelação (FAC) e Autocorrelação Parcial (FACP) de cada modelo verificando se os resíduos não se apresentam autocorrelacionados. As FAC e FACP (Figura 6) satisfizeram esta condição e encontraram-se dentro dos limites de confiabilidades.
Figura 6: Função de Autocorrelação (FAC) e Função de AutocorrelaçãoParcial (FACP)

A FAC apresentou φ1negativo e a FACP decai exponencialmente, mas esta apresentando sinais positivos e negativos denominando uma parte do modelo como autorregressivo demonstrando e captando a sazonalidade deste modelo.
Figura 7: Gráfico dos resíduos da série atual e da série com uma diferença
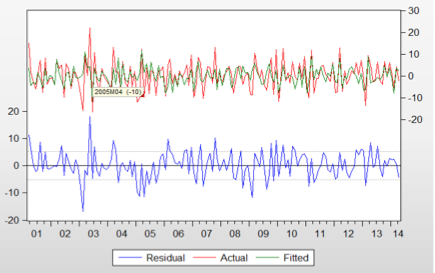
A figura 7 esta demonstrando o comportamento do resíduo da série atual e do ajustado.
Figura 8: Correlação dos Resíduos

Conforme a figura 8 ela descreve que os resíduos são ruídos branco, foi realizada a análise dos resíduos assim como no primeiro modelo e todas as suposições foram verificadas, sendo assim o modelo selecionado cumpriu com a condição dos resíduos serem ruído branco – RB e não autocorrelacionados. Auxiliando na escolha do melhor modelo. Portanto o modelo representativo da série está em negrito na tabela abaixo:
Figura 9: Gráfico da Previsão do consumo de combustíveis e seus derivados

Na Figura 9 Observa-se que o gráfico das previsões do consumo de combustíveis e seus derivados, para ano de 2015 não tem muita diferença do gráfico da série atual, também observa-se que ele terá sazonalidades em alguns períodos.
Tabela 5 - Modelos significativos para a Série

4. Conclusão
A análise descritiva do consumo de combustíveis e derivados destacou que o maior consumo ocorreu no período de 2013 no estado do Rio Grande do Sul. A metodologia Box &Jenkins proporcionou um eficiente papel para representar as séries em estudo, captando os efeitos sazonais ocorridos nos preços e descrevendo o comportamento da série.
O estudo realizado teve como objetivo encontrar um modelo de previsão confiável para a venda no varejo de combustíveis e lubrificantes, no Estado do Rio Grande do Sul no ano de 2015, pois como se sabe cada vez há mais veículos trafegando no estado, também e o petróleo é um recurso natural não renovável, a partir daí surgiu o interesse em demonstrar à quantidade de combustíveis e lubrificantes utilizados no estado.
Assim através dos resultados obtidos verifica-se que a previsão de melhor qualidade ou que melhor se ajustou aos dados, segundo os critério utilizados neste presente estudo, foi o modelo SARIMA(1,1,1)12.
Com isso chega-se à conclusão de que a venda de combustíveis e lubrificantes pode se beneficiar da utilização de métodos de previsão a partir de séries temporais, pois esta metodologia possibilitou efetuar a análise das informações tentando retirar conhecimento útil das mesmas e assim predizer o futuro, por meio da análise dos dados estudados e com isso construir um modelo que permita antever a evolução futura da série temporal.
Referencias Bibliograficas
AMARO. Silveira Raphae, SOUZA Mendonça, Adriano.(2014); Análise da Série de Retornos do Índice Bovespa utilizando como instrumental modelos Box-Jenkins. Espacios. Vol. 35 (Nº 12) Año 2014. Pág. 14
ALMEIDA, et al. (2013); Análise e previsão nos preços dos combustíveis no mercado de Pernambuco: Uma abordagem através de séries temporais Univariadas. XIII JORNADA DE ENSINO, PESQUISA E EXTENSÃO – JEPEX – UFRPE: Recife, 09 a 13 de dezembro.
BOX, G. E. O.; JENKINS, G.M. (1970); Time series Analysis: Forecasting and Control. San Francisco: Holden-Day.
BUENO, R. L. S. (2008); Econometria de Séries Temporais. São Paulo: Cengage Learning.
GURGEL, Alexandre. NETO, Afonso Avelino Dantas (s/a);Refino De Petróleo E Petroquímica. Departamento de Engenharia Química. UFRN.
MORETTIN, P. A.; TOLOI, C. M. C. (2004);Análise de Séries Temporais. 1ª edição. Editora Edgard Blucher.
PEREIRA, Zulema L.; Requeijo, José G. (2008);Planejamento e Controlo Estatístico dos Processos, Prefácio.
SOUZA. Mendonça, Francisca (2006);Modelos Box & Jenkins Aplicados a Previsão de Demanda de Leitos Hospitalares. Monografia de Especialização. UFSM.
VASCONCELLOS, M. A. S.; ALVES, D. (2002); Manual de econometria. São Paulo. Atlas.
LIMA, C, R; Góis, R M; Ulises, C. (2007);Previsão de preços futuros de Commodities agrícolas com diferenciações inteira e fracionária, e erros heteroscedásticos. Rev. Econ. Sociol. Rural vol.45 no.3 Brasília July/Sept. [Acessado em 06 de junho de 2014]. Disponível em: http://www.scielo.br/scielo.php?pid=S0103-20032007000300004&script=sci_arttext.
SOUZA, Francisca Mendonça; ALMEIDA, Silvana Gonçalves; SOUZA, Adriano Mendonça; LOPES, Luis Felipe Dias; ZANINI, Roselaine Ruviaro (2011); Previsão do preço da gasolina para a região sul do Brasil. IJIE – Iberoamerican Journal of industrial Engineering. v.3, n.1, p. 234-248.
1.Email: claudiaramser@hotmail.com
2. Universidade Federal de Santa Maria – UFSM amsouza@smail.ufsm.br