Espacios. Vol. 36 (Nº 09) Año 2015. Pág. 13

Combinação de previsões das vendas no setor de suplementação animal: um estudo de caso com ajustes de especialistas

Combination of sales forecasts in the animal supplement industry: a case study with experts settings

Rodolfo Benedito da SILVA 1; Liane WERNER 2

Recibido: 09/01/2015 • Aprobado: 16/02/2015

Contenido

1. Introdução

2. Técnicas de previsões

3. Combinação de previsões

4. Ajuste de previsões

5. Procedimentos metodológicos

6. Apresentação e discussão dos resultados

7. Considerações finais

Referências

1. Introdução

A previsão de demanda tem desempenhado um papel importante dentro das organizações, pois através dela é possível obter uma declaração antecipada do comportamento do mercado em momentos futuros. Tendo em mãos estas informações, os gestores podem definir planos para atender a demanda, alocando de modo eficaz os recursos disponíveis, tais como, mão-de-obra, recursos financeiros, estoques, dentre outros.

Tendo em vista que o processo de previsão envolve incertezas, não basta somente obter as informações para garantir a eficiência da aplicação da ferramenta. É preciso que estas informações apresentem boa acurácia, de modo que sejam mais confiáveis, conforme exposto por Abraham e Ledolter (2005).

Existem diversos métodos de previsão de demanda, no entanto, muitos deles usam as informações utilizando uma única técnica de previsão (WERNER e RIBEIRO, 2006). Este fato pode comprometer a acurácia da previsão, pois não permite que outras informações possam ser incorporadas no processo. Para sanar esta lacuna, é necessário agregar diversas previsões em uma única e nova previsão (ARMSTRONG, 2001; WERNER, 2004). Esta integração tem permitido reduzir os erros de previsão e obter previsões mais acuradas em relação às previsões individuais (CLEMEN, 1989; RODRIGUES e STEVENSON, 2013).

Segundo Werner (2004), a obtenção de previsões confiáveis requer a utilização de várias técnicas, de modo a captar o maior número de informações disponíveis. O processo de incorporação de diferentes previsões obtidas de diferentes técnicas é realizado através do método conhecido como combinação de previsões.

A principal vantagem da combinação de previsões é a incorporação de conhecimentos sobre a natureza e comportamento das variáveis estudadas no processo de previsão de demanda, aliado às informações contextuais obtidas dos dados históricos, de fontes de informações públicas e/ou de fontes internas da empresa. Especialistas com domínio de conhecimento possuem capacidade de julgar quais informações são importantes para o processo de previsão (WEBBY et al., 2001). Estudos como de Armstrong e Collopy (1998), Lemos (2006) e Rodrigues e Stevenson (2013) apresentam evidências de que a combinação de previsões tem apresentado resultados satisfatórios quanto à acurácia.

Este estudo fará uma adaptação do modelo integrado de previsão proposto por Werner (2004), para prever demanda de produtos destinados à suplementação animal. Para isto, serão considerados dados históricos que refletem o comportamento da demanda em períodos anteriores, dados históricos das variáveis que interferem na demanda dos produtos e dados de especialistas que contribuirão com conhecimentos para realizar os ajustes na previsão integrada com o intuito de obter a previsão final.

2. Técnicas de previsões

As técnicas de previsões, aqui chamadas de previsões individuais, são obtidas através de modelos quantitativos ou métodos qualitativos. Os métodos quantitativos são aqueles que usam dados históricos para estimativas de demandas em momentos futuros. Para isto, requerem a construção de modelos matemáticos a partir desses dados históricos, dispostos em forma de séries temporais. Tais técnicas utilizadas para a construção desses modelos são conhecidas por técnicas de forecasting (PELLEGRINI, 2000).

As técnicas quantitativas se dividem em dois grupos, dependendo de como as causas da demanda são consideradas nos modelos. No primeiro, enquadram-se os modelos baseados em séries temporais, aqueles que não buscam conhecer as causas da demanda e sim descrever o comportamento desta demanda em função de dados passados. Já no segundo grupo, encontram-se os modelos causais, que se preocupam em identificar e compreender as variáveis que interferem na demanda (MAKRIDAKIS et al., 1998). Salienta-se que os dois grupos são focos deste estudo.

Dentre as técnicas baseadas em séries temporais, encontram-se a média móvel, suavização exponencial e o método de Box-Jenkins. Já entre as técnicas baseadas nos modelos causais, têm-se os modelos obtidos via análise de regressão linear simples ou múltipla.

Como este artigo foca no uso de modelos de suavização exponencial para previsão estatística, somente estes modelos serão delineados neste referencial teórico. O modelo de Suavização Exponencial Simples é um método que obtêm a previsão com base na previsão anterior, acrescentando o erro auferido nesta previsão, corrigido por um coeficiente de ponderação (HOLT, 2004).

Para casos em que os dados históricos apresentam tendência linear e não apresentam sazonalidade, Makridakis et al. (1998), recomendam que seja utilizado o modelo linear de Holt. Este método, também conhecido como Suavização Exponencial Dupla, contempla o nível e a tendência da série temporal empregando duas constantes de suavização, α e β (com valores entre 0 e 1, e não relacionados).

Por fim, tem-se o modelo de Holt-Winters que é indicado para casos em que as séries temporais apresentam padrão de demanda com tendência linear e sazonalidade. Este modelo faz aplicação de equações de suavização para estimar o nível, a tendência e a sazonalidade da série temporal estudada no processo de previsão (MAKRIDAKIS et al., 1998). Tal método apresenta duas abordagens distintas, as quais dependem da forma como é modelada a sazonalidade: forma multiplicativa ou aditiva. A forma multiplicativa é indicada para séries temporais em que a amplitude da sazonalidade varia com o nível da demanda. A forma aditiva é apropriada para séries temporais cuja amplitude da sazonalidade é independente do nível de demanda (HOLT, 2004).

Os modelos causais, aqueles que buscam conhecer as causas da demanda e as variáveis que interferem na mesma, são estruturados por análise de regressão e podem ser divididos em: i) regressão linear simples; ii) regressão linear múltipla. A regressão linear simples considera apenas um único regressor ou preditor X e uma variável dependente ou variável de resposta Y de modo linear (MONTGOMERY e RUNGER, 2009). A regressão simples é baseada na correlação linear, medida pelo coeficiente linear de Pearson. Quando se eleva este coeficiente ao quadrado, têm-se o coeficiente de determinação, que é um indicador de qualidade da regressão realizada. Os valores deste indicador variam de 0 a 1 e, valores próximos a 1 são desejáveis e indicam que as variáveis dependente e independente estão fortemente correlacionadas (MONTGOMERY e RUNGER, 2009), o que indica que um modelo de regressão será adequado.

Segundo Werner (2004), em muitas ocasiões, dificilmente uma variável dependente Y se relaciona com apenas uma única variável explicativa, por exemplo, a demanda de um determinado produto depende de diversas outras variáveis, como por exemplo: preço, preço do concorrente, renda do consumidor. Para situações como esta, a regressão linear múltipla deve ser utilizada.Sendo assim, a primeira etapa é coletar dados históricos de cada variável independente. A aplicação do modelo de regressão linear múltipla requer a listagem de todas as variáveis que interferem na demanda de Y. A lista inicial de variáveis independentes pode ser obtida com base nos seguintes fatores: i) experiência de especialistas; ii) disponibilidade dos dados, e; iii) restrições de tempo e custo. Tal lista deve ser filtrada utilizando procedimentos formais, tais como regressões de subconjuntos de variáveis ou análise de componentes principais de todas as variáveis (incluindo Y) para decidir quais são as variáveis importantes. De modo geral, uma combinação de procedimentos é utilizada para obter a lista final de variáveis explanatórias (MAKRIDAKIS et al., 1998). Neste estudo, estas variáveis foram selecionadas através da aplicação do método Analytic Hierarchy Process conforme proposto por Silva (2014).

Quando se trata da utilização de métodos quantitativos de previsão, há necessidade de mensurar o desempenho das modelagens, com o intuito de identificar quão acurada é esta previsão. Segundo Paliwal e Kumar (2009), diversos estudos utilizaram as medidas MAPE (Mean Absolute Perceptual Error), MAE (Mean Absolute Error) e MSE (Mean Square Error) para medir o desempenho das modelagens.

Por sua vez, as técnicas qualitativas obtêm previsões futuras através de opiniões, intuição, indicadores, pesquisas de mercado, experiência de especialistas ou informações subjetivas. De acordo com Wright et al. (1996) e Goodwin (2002), a opinião está envolvida em toda e qualquer técnica de previsão de demanda.

Tendo em vista a natureza subjetiva, estes métodos geralmente são utilizados quando os dados são escassos para formulação de estratégias, desenvolvimento de novos produtos e tecnologias que possuem introdução e aceitação de mercado desconhecidas e também no desenvolvimento de planos de longo prazo (MAKRIDAKIS; WHEELWRIGHT; HYNDMAN, 1998). Diversas técnicas de previsão subjetiva são encontradas na literatura, dentre eles destacam-se: i) método Delphi; ii) analogia histórica; iii) pesquisa de mercado; e iv) painel de consenso.

3. Combinação de previsões

A combinação de duas ou mais técnicas de previsões tem apresentado boa aceitação e demonstrado evidências de um aumento na acuracidade das previsões finais (WEBBY e O'CONNOR, 1996; COSTANTINI e PAPPALARDO, 2010). Na visão de Lawrence et al. (2006), isto se deve ao fato de que as previsões, quando combinadas, agregam informações de diversas fontes, aumentando deste modo as informações sob as quais a previsão está fundamentada.

A combinação de previsões parte do seguinte princípio: baseando-se em conjunto de dados históricos e informações contextuais, são gerados os modelos de previsões com base em diferentes métodos (método 1, método 2, ..., método n), obtendo-se n previsões. Posteriormente, estas previsões são combinadas e gera-se uma única previsão final, conforme pode ser visto na Figura 1.

Figura 1: Combinação de previsões

Fonte: Adaptado de Webby e O'Connor (1996, p. 100)

Na literatura, pode-se encontrar diversos estudos que propõem a combinação de previsões. No entanto, para fazer uso desta combinação e considerar as variáveis que podem afetar as previsões, há necessidade, segundo Werner (2004), de saber quais técnicas usar e como proceder (quais métodos utilizar para combiná-las).

Existem duas abordagens para combinação de previsões, sendo uma de abordagem objetiva e outra de abordagem subjetiva. Segundo Werner (2004), "a abordagem objetiva reflete os métodos que fazem uso da matemática, de forma que os resultados possam ser repetidos. A abordagem subjetiva inclui esforços intuitivos para combinar previsões-base, empregando conhecimento e opinião individual ou de grupo".

Os métodos objetivos de combinação foram originados a partir do estudo de Bates e Granger (1969). Estes autores sugeriram o método de combinar as previsões por meio de uma combinação linear de duas previsões objetivas não viciadas (ou devidamente corrigidas), atribuindo peso k para a primeira previsão e peso (1 - k) para a segunda, conforme pode ser visto na equação (1).

onde: C é valor combinado, f1é a previsão 1, f2 é a previsão 2 e k é o peso da previsão 1.

Bates e Granger (1969) recomendam ainda a atribuição de um peso maior à previsão que apresenta os menores erros. Para isto, propuseram a minimização da variância dos erros da previsão combinada.

Após a proposta de obtenção de pesos via variância mínima de Bates e Granger (1969), apresentada anteriormente, De Gooijer e Hyndman (2006) afirmam que diversos métodos já foram propostos para selecionar os pesos combinados, sendo que a média aritmética é a técnica de combinação mais utilizada. O método da média aritmética, composto por duas previsões, é apresentado na equação (2).

onde: C é o valor combinado, f1é a previsão 1 e f2 é a previsão 2.

De acordo com Werner (2004), apesar de não ter pesos ótimos, a média pode gerar resultados melhores que os métodos mais sofisticados. Esta mesma conclusão também foi exposta por Clemen (1989). Já Armstrong (2001) relata que, embora a média aritmética das previsões demonstre ser relativamente robusta e mais acurada que métodos mais elaborados, diversos autores continuaram na busca pelo melhor método de combinação.

4. Ajuste de previsões

O ajuste de previsões baseada na opinião de especialistas consiste em uma maneira de acrescentar informações no processo de previsão. Para isto, os especialistas devem ter disponíveis informações contextuais não capturadas pelo modelo estatístico e também domínio de conhecimento para fazer a interpretação de modo correto dos eventos inesperados e das informações informais (STAUDT, 2011). De acordo com Armstrong e Collopy (1998), o ajuste de previsões é uma das maneiras mais comuns de integração entre métodos estatísticos e opiniões de especialistas.

Nas visões de Sanders e Ritzman (2001) a decisão de quando e como usar o julgamento no ajuste de previsões estatísticas deve-se considerar cinco princípios, sendo eles:i) a previsão estatística deve ser ajustada quando houver domínio de conhecimento suficiente; ii) ajustar quando há alto grau de incerteza; iii) ajustar quando existe conhecimento de mudanças no ambiente; iv) o processo de ajuste deve ser estruturado; e v) levar em consideração a integração mecânica de previsões estatísticas e por julgamento.

Webby e O'Connor (1996) recomendam três maneiras de ajuste por julgamento no resultado de uma previsão estatística: i) ajuste sem contexto; ii) ajuste contextual e; iii) ajuste estruturado. A primeira situação pode ser utilizada quando o previsor verifica que a previsão está imprecisa, apesar do mesmo não conseguir associar nenhuma informação contextual com a série, ou seja, sem o uso de qualquer processo de raciocínio. Já o ajuste contextual é usado quando há informações contextuais disponíveis e o especialista ajusta a previsão inicial com o intuito de incorporar os efeitos destas informações. Comumente este ajuste é eficaz, apesar de ser difícil afirmar que o aumento da acuracidade se dá apenas pelo contexto, visto que a experiência e a motivação do especialista podem influenciar. Por sua vez, o ajuste estruturado leva em consideração a aplicação de metodologias estruturadas para construir um julgamento sem informalidade, pois a principal crítica do ajuste por julgamento está em ser, muitas das vezes, de natureza empírica.

O ajuste estruturado pode ser realizado simplificadamente por meio de um procedimento formal de conhecimento dos especialistas ou até mesmo fazendo-se uso de um sistema de suporte à decisão como, por exemplo, o método Analytic Hierarchy Process – AHP (STAUDT, 2011). Werner (2004) fez uso de uma estrutura baseada no AHP para realizar ajustes na previsão de demanda em uma empresa de assistência técnica de computadores. Já Lim e O'Connor (1996), utilizaram o método julgamento revisado para estruturação do ajuste de previsão fictícia de vendas de refrigerantes. Segundo Werner (2004), realizar um ajuste na previsão baseada na opinião de especialistas ainda é um assunto pouco explorado.

Para se tornar útil, o ajuste baseado na opinião deve acrescentar informações que não são consideradas pela previsão estatística de modo estruturado (ARMSTRONG e COLLOPY, 1998). O uso de uma estrutura de ajuste tem por objetivo minimizar a incorporação de viés, intrínseco à tomada de decisão humana (WEBBY e O'CONNOR, 1996).

5. Procedimentos metodológicos

Tendo em vista os objetivos propostos neste estudo, esta pesquisa é caracterizada como explanatória e descritiva. Segundo Gil (2007), a pesquisa explanatória busca possibilitar mais familiaridade com o problema, com o intuito de torná-lo mais explícito ou de construir hipóteses. Na maioria das vezes estas pesquisas envolvem: i) levantamento bibliográfico; ii) entrevistas com pessoas que tiveram experiências práticas com o problema estudado; e iii) análise de situações que estimulem a compreensão. Por sua vez, a pesquisa descritiva exige do pesquisador diversas informações a respeito do objeto de pesquisa. Este tipo de pesquisa busca descrever os fatos e fenômenos de determinada realidade (GIL, 2007). A partir da compreensão desses tipos de pesquisas, procedeu-se o estudo do seguinte modo.

Inicialmente foram obtidas as previsões de demanda através da adaptação do método proposto por Werner (2004). Esta adaptação consistiu primeiramente na exclusão da previsão baseada na opinião de especialistas, devido à restrição quanto ao número mínimo, sendo recomendado pela literatura entre cinco e vinte especialistas. Por se tratar de uma empresa de médio porte, não há número mínimo suficiente de especialistas que possam contribuir com a previsão. Sendo assim, foram obtidas somente as previsões individuais: estatística e via regressão e, posteriormente, realizou-se a combinação destas duas previsões pelos métodos de variância mínima e média aritmética. Após selecionar o modo de combinar as previsões, foi realizado o ajuste por meio da opinião de especialistas, fazendo-se uso de uma estrutura simplificada baseada no método AHP (Processo Hierárquico Analítico) e, posteriormente, obteve-se a previsão final. A Figura 2 apresenta a adaptação do modelo proposto por Werner (2004) utilizado neste estudo.

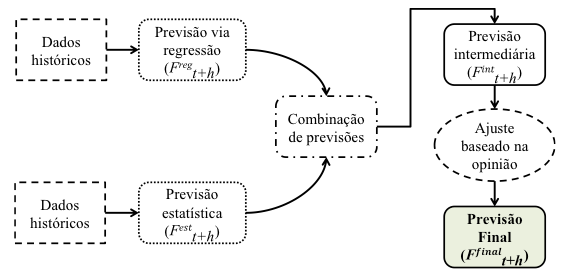
Figura 2: Adaptação do modelo composto de previsão proposto por Werner (2004)

Fonte: Adaptado de Werner (2004, p. 98)

Para a previsão via regressão, além dos dados históricos de demanda da empresa (variável dependente), foi necessário realizar a coleta, tratamento e análise de dados históricos das variáveis independentes que interferem na demanda dos produtos destinados a suplementação animal. Os dados das variáveis independentes utilizados neste estudo foram selecionados através da técnica de decisão multicriterial AHP (Processo Hierárquico Analítico) com três especialistas da empresa, conforme o estudo realizado por Silva (2014), de onde foram selecionadas as variáveis a serem avaliadas na modelagem via regressão, i) preço da arroba do boi; ii) número de animais abatidos; iii) tamanho do rebanho; e iv) condições climáticas.

Na construção do modelo estatístico, foi realizada a análise da série temporal para identificar o comportamento da mesma e selecionar o modelo que melhor se ajustou aos dados. Foram utilizados dados históricos de vendas em toneladas disponibilizados no software de gestão da empresa. Para isto, foram reunidos dados de janeiro de 2008 a agosto de 2013, totalizando 68 períodos, dos quais 56 períodos foram utilizados na modelagem (treino) e 12 períodos para o teste de previsões.

Neste estudo, os desempenhos das modelagens foram analisados através das seguintes medidas de acurácia: MAPE (Mean Absolute Perceptual Error), MAE (Mean Absolute Error) e MSE (Mean Square Error).

6. Apresentação e discussão dos resultados

6.1. Análise dos dados

A Figura 3 apresenta os dados históricos coletados da demanda. Através desta figura é possível visualizar a relação entre os valores demandados (toneladas) em função do período de observação e também o comportamento e as principais características da série temporal, a saber: que a série apresenta tendência levemente positiva por meio da linha tracejada. Além disso, sugere-se comportamento sazonal da série com comprimento sazonal de 12 meses, indicada através dos picos elevados da demanda nos meses de julho de cada ano. Sendo assim, a descrição realizada, sugere que a série é não estacionária e sazonal.

Figura 3: Dados históricos da demanda

6.2. Previsão estatística

Para os dados apresentados na Figura 3, foram obtidas primeiramente as previsões via modelagem estatística pelo modelo aditivo de Holt-Winters, seguindo a recomendação de Makridakis et al. (1998), visto que a série apresenta comportamento sazonal e a amplitude de sazonalidade é independente do nível da demanda.

6.3. Previsão via modelo causal (regressão)

Após a obtenção da previsão estatística através do modelo aditivo de Holt-Winters, obteve-se a previsão via regressão. Inicialmente, realizou-se uma regressão linear múltipla utilizando o método dos Mínimos Quadrados Ordinários (MQO) com todas as variáveis selecionadas em Silva (2014): i) preço da arroba do boi; ii) número de animais abatidos; iii) tamanho do rebanho; e iv) condições climáticas.

Para esta modelagem, verificou-se através da análise de variância um modelo significativo, com p-value inferior a 0,0005. No entanto, o modelo apresentou um coeficiente de determinação ajustado baixo (R2 = 0,477) e os coeficientes das três primeiras variáveis demonstraram não serem significativos, a um nível de significância de 5%. Devido a este baixo poder de explicação do modelo, outros modelos de regressão foram testados, tais como, os modelos logarítmico e polinomial, levando em consideração apenas a variável condições climáticas, que demonstrou ser significativa para a modelagem (p-value= 0,000), visto que mesmo fazendo diversos tratamentos das outras variáveis, os seus respectivos coeficientes continuaram não significantes.

Inicialmente realizou-se um estudo da correlação entre o volume de vendas e a variável condições climáticas, através do coeficiente de correlação de Pearson, cujo valor foi de – 0,842. Deste modo, verifica-se uma forte correlação negativa entre as variáveis, o que significa que, quanto menor for o valor das condições climáticas, medida através do índice de pluviosidade (precipitação), maior será o volume demandado, como pode ser observado através das Figuras 4 e 5, respectivamente.

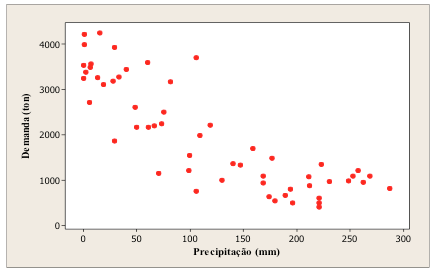
Figura 4: Correlação entre a demanda (ton) e precipitação (mm)

-----

Figura 5: Séries históricas da demanda (ton) e precipitação (mm)

Constata-se através da Figura 5 que nos meses em que há redução considerável de chuvas, ou seja, valores da precipitação baixos ou zero, que geralmente ocorre entre os meses de abril e setembro de cada ano, a demanda se eleva consideravelmente. Isto se deve ao fato que nos períodos de pouca chuva as pastagens diminuem e os produtos comercializados pela empresa são utilizados como alimento substituto para garantir a sobrevivência dos animais.

Posteriormente a estas análises, procedeu-se o estudo buscando encontrar um modelo que apresentasse um melhor poder de explicação. Após diversos testes e análises, encontrou-se um modelo de regressão polinomial de 2ª ordem, com coeficiente de determinação ajustado razoável (R2 = 0,768), que é representado através da equação 3.

em que: Y: demanda ou volume de vendas (ton); X: condições climáticas ou pluviosidade (mm).

A Figura 6 apresenta as duas previsões individuais modeladas e selecionadas a partir de um conjunto de validações.

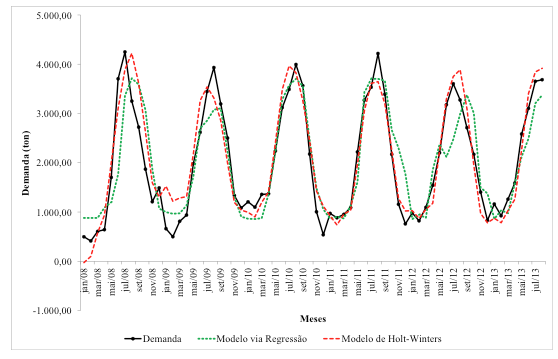
Figura 6: Previsões individuais

6.4. Combinação de previsões

Após a obtenção das duas previsões individuais apresentadas na seção anterior, realizaram-se os ajustes das previsões combinadas, via variância mínima e média aritmética. A previsão combinada via variância mínima foi obtida considerando o formato sem correlação entre os erros das previsões individuais.

A Figura 7 apresenta o comportamento destas duas técnicas de previsões combinadas. É possível verificar através desta Figura, que as previsões combinadas via variância mínima e média aritmética apresentam comportamentos similares. No entanto, somente através da Tabela 2 que é possível ter uma noção real da acurácia dos modelos analisados.

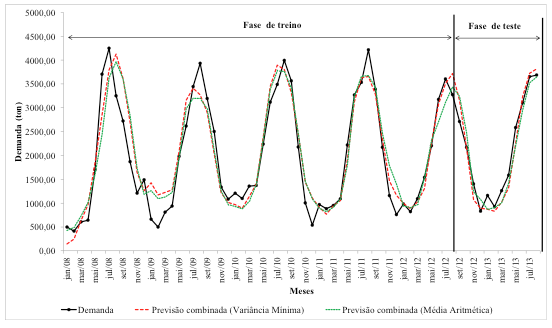
Figura 7: Previsões combinadas

A Tabela 1 apresenta as medidas de acurácia Erro Absoluto Percentual Médio (MAPE), Erro Absoluto Médio (MAE) e Erro Quadrático Médio (MSE) para as previsões individuais e previsões combinadas obtidas na fase de teste. Os valores para estas medidas de acurácia que se encontram entre parênteses, são referentes aos 68 períodos da série temporal.

Tabela 1: Medidas de acurácia para os modelos analisados

Pode-se constatar, através da Tabela 1, que as previsões combinadas, tanto via regressão mínima quanto através da média aritmética, apresentaram desempenhos superiores (melhores resultados) para todas as medidas de acurácia analisadas em relação às técnicas de previsões individuais, ficando na primeira e segunda colocação, respectivamente.

Na terceira posição, encontra-se o modelo de Holt-Winters que apresentou os menores resultados para MAPE, MAE e MSE em comparação ao modelo via regressão, que ficou na última colocação. Com base nestes resultados, a previsão combinada via variância foi utilizada no estudo para a obtenção da previsão final.

6.5. Ajuste da previsão combinada e obtenção da previsão final

Nesta etapa é realizado o ajuste da previsão combinada através da opinião de especialistas e, posteriormente, obtêm-se a previsão final conforme proposto por Werner (2004). Para isto, faz-se necessário usar um método estruturado visando o aprimoramento da acurácia da previsão combinada. Werner (2004) recomenda fazer uso de uma estrutura simplificada baseada no método AHP (Processo Hierárquico Analítico), seguindo os passos descritos a seguir. O ajuste da previsão foi realizado por somente dois especialistas, visto que o terceiro não compunha mais o quadro da empresa no momento da realização desta etapa.

Passo 1: Fixação do percentual máximo e mínimo de ajuste - o especialista 1, estabeleceu um percentual máximo de 30% e mínimo de -30%, indicando que de um período para o outro a demanda poderá ter um acréscimo ou uma de redução de 30%. Já o especialistas 2fixou um percentual máximo de 40% e mínimo de -25%.

Passo 2: Listagem dos fatores que impactam na demanda - neste momento os especialistas fizeram a listagem de fatores que influenciam o comportamento da demanda, conforme apresentado na Tabela 4.

Passo 3: Mensuração do impacto de cada um dos fatores identificados - aqui os especialistas atribuíram pesos para os fatores, com o intuito de identificar a influência (fraca, moderada ou forte) sobre demanda, fazendo-se uso da escala de importância proposta por Saaty (1991), no desenvolvimento do método AHP. Após esta atribuição de pesos, os mesmos foram normalizados através da relação entre o peso do fator i e a soma de todos os pesos.

Passo 4: Mensuração da opinião dos especialistas - nesta etapa os especialistas informaram como cada fator irá contribuir na alteração da demanda para o próximo período, de modo que se a contribuição for de aumento na demanda, optaram pelo valor +1, se a contribuição for de queda na demanda optaram pelo valor -1.

A Tabela 2 apresenta a listagem dos fatores com seus respectivos pesos, pesos normalizados, bem como os impactos de cada um deles na demanda para o próximo período.

Tabela 2: Opiniões e pesos dos especialistas para os fatores que impactam na demanda

Passo 5: Cálculo das médias ponderadas - os resultados obtidos da soma de produto entre os pesos normalizados e o impacto de cada fator corresponde à média ponderada que se deseja obter neste passo. Deste modo, para o especialista 1 obteve-se a média 0,220 e para o especialista 2 a média foi de 0,122.

Passo 6: Cálculo do ajuste percentual - como os resultados das médias ponderadas foram positivos, realiza-se a multiplicação de tais médias pelo percentual máximo.No caso do especialista 1, o valor de ajuste percentual foi de 0,220 x 0,35 = 7,70%. Sendo assim, o especialista sugere que a previsão combinada deve ter um acréscimo de 7,70%. Para o especialista 2, o valor de ajuste obtido foi de 0,122 x 0,35 = 4,27%, ou seja, na visão do especialista 2 a previsão combinada deve ter um acréscimo de 4,27%. A média aritmética dos percentuais de ajuste dos dois especialistas resulta no percentual de ajuste médio, sendo 5,985%.

Passo 7: Obtenção da previsão final - para proceder com o ajuste final da previsão combinada, adiciona-se o valor 1 ao ajuste percentual médio encontrado e multiplica-se o resultado desta soma pelo valor da previsão combinada, assim como pode ser visto na Tabela 3.

Tabela 3: Obtenção da previsão final

O valor real da demanda observado para setembro de 2013 foi de 3.338,93 toneladas. Deste modo, o volume previsto final foi superior em 187,60 toneladas, o que corresponde que a demanda real foi inferior em 5,32% em relação ao valor previsto.

7. Considerações finais

Este estudo realizou a aplicação na área de suplementação animal para obter a previsão de demanda com base no modelo apresentado por Werner (2004). Para tanto, foram considerados dados históricos de vendas em toneladas, dados históricos das variáveis que impactam na demanda dos produtos selecionadas em Silva (2014) e também informações de especialistas que contribuíram na realização dos ajustes da previsão combinada para obtenção da previsão final.

Tendo em vista o comportamento da série temporal analisada, na previsão estatística foi utilizado o modelo aditivo de Holt-Winters, seguindo a recomendação de Makridakis; Wheelwright; Hyndman (1998). Já na obtenção da previsão causal obtida via regressão, levou-se em consideração na modelagem apenas a variável condições climáticas (precipitação), visto que as outras três variáveis demonstraram não impactar na demanda a um nível de significância de 5%. Além disso, foi possível verificar uma forte correlação negativa (r = - 0,842) entre a demanda e esta variável, indicando que, quanto menor o volume de chuvas, maior o volume demanda de produtos produzidos e comercializados pela empresa. Após diversas análises, chegou-se a um modelo polinomial de 2ª ordem que apresentou um coeficiente determinação ajustado razoável (R2 = 0,768) para obter a previsão via modelo de regressão.

Através das medidas de acurácia analisadas, constatou-se que as previsões combinadas apresentaram desempenhos superiores em relação às técnicas de previsões individuais. Diante deste contexto, a previsão combinada por meio da variância mínima foi selecionada para a obtenção da previsão final. Os modelos de Holt-Winters e de regressão obtiveram a terceira e quarta colocação, respectivamente, no ranking de desempenhos.

O ajuste da previsão combinada foi feito levando em consideração a opinião de dois especialistas da empresa. Para realizar o ajuste, foram estabelecidos os percentuais máximos e mínimos que a demanda pode aumentar ou diminuir de um período para outro. Também foram listados os fatores que mais impactam na demanda e os pesos e a intensidade dos fatores para o próximo período, com o intuito de obter o ajuste percentual médio a ser utilizado na obtenção da previsão final. Este ajuste percentual demonstrou que os especialistas sugerem um acréscimo de 5,985% na previsão combinada de um período para outro, sendo a previsão para o período de setembro/2013 igual a 3.526,53 toneladas. Recomenda-se que as intensidades dos fatores sejam revisadas para previsões futuras, pois estas podem impactar de modo diferente na demanda de período a período.

Por fim, foi possível verificar que o método de combinação de previsões destaca-se em relação às técnicas individuais. Os resultados obtidos demonstraram que a previsão combinada via variância mínima não deve ser desconsiderada pelos previsores, bem como pelos interessados na previsão. Além disso, o modelo de previsão adaptado demonstrou ser apropriado para obter previsões combinadas e ajustadas também no setor de suplementação animal.

Referências

ABRAHAM, B.; LEDOLTER, J. Statistical Methods for Forecasting. New York: John Wiley & Sons, 2005.

ARMSTRONG, J. S. Principles of Forecasting: A Handbook for Researchers and Practitioners. Kluwer Academic Publishers. 2001.

ARMSTRONG, J. S.; COLLOPY, F. Integration of Statistical Methods and Judgment of Time Series Forecasting: Principles for Empirical Research. In: WRIGHT, G. & GOODWIN, P. (Ed.) Forecasting with Judgment. Wiley & Sons, 1998.

BATES, J. M.; GRANGER, C. W. J. The Combining of Forecasts. Operational Research Quarterly. v.20, n.4, p. 451-468, 1969.

CLEMEN, R. T. Combining Forecasts: A Review and Annotated Bibliography. International Journal of Forecasting. v. 5, p.559-583, 1989.

COSTANTINI, M; PAPPALARDO, C.A. Hierarchical procedure for combination of forecasts. International journal of forecasting, v. 26, p. 725-743, 2010.

DE GOOIJER, J. G.; HYNDMAN, R. J. 25 years of time series forecasting. International Journal of Forecasting, v. 22, p. 443–473, 2006.

GIL, A. C. Como elaborar projetos de pesquisa. 4. ed. São Paulo: Atlas, 2007.

GOODWIN, P. Integration Management Judgement and Statistical Methods to Improve Short-term Forecasts. Omega. The International Journal of Management Science. v.30, p.127-135, 2002.

HOLT, C. C. Forecasting Seasonals and Trends by Exponentially Weighted Moving Averages. International Journal of Forecasting. v. 20, n. 1, p. 5-10, 2004.

LAWRENCE, M.; GOODWIN, P.; O'CONNOR, M.; ONKAL, D. Judgmental forecasting: A review of progress over the last 25years. International Journal of Forecasting, v. 22, p.493-518, 2006.

LIM, J. S.; O'CONNOR, M. Judgmental forecasting with time series and causal information. International Journal of Forecasting, v. 12, p. 139-153, 1996.

LEMOS, F. O. Metodologia para seleção de métodos de previsão de demanda. 2006. 183p. Dissertação (Mestrado em Engenharia de Produção), Escola de Engenharia, Universidade Federal do Rio Grande do Sul, Porto Alegre, 2006.

MAKRIDAKIS, S.; WHEELWRIGHT, S.; HYNDMAN, R. J. Forecasting: Methods ans Applications. 3ª ed. New York, John Wiley & Sons, 1998.

MONTGOMERY, D.C.; RUNGER, G.C. Estatística aplicada e probabilidade para engenheiros. 4. ed. Rio de Janeiro: LTC, 2009.

PALIWAL, M.; KUMAR, U. A Neural networks and statistical techniques: A review of applications. Expert Systems with Applications, v. 36, p. 2-17, 2009.

PELLEGRINI, F. R. Metodologia para implementação de sistemas de previsão de demanda. 2000. 146p. Dissertação (Mestrado em Engenharia de Produção), Escola de Engenharia, Universidade Federal do Rio Grande do Sul, Porto Alegre, 2000.

RODRIGUES, B. D; STEVENSON, M. J. Takeover prediction using forecast combinations. International Journal of Forecasting. v. 29, n. 4, p. 628-641, 2013.

SAATY, T.L. The Analytic Hierarch Process. RWS Publications, 1996.

SANDERS, N. R.; RITZMAN, L. P. Judgmental adjustment of statistical forecasting. In: ARMSTRONG, J. S. Principles of forecasting: a handbook for researches and practitioners. Dordrecht: Kluwer Academic Publishers, p. 405-416, 2001.

SILVA, R. B. Previsão de demanda no setor de suplementação animal usando combinação e ajuste de previsões. 2014. 64p. Dissertação (Mestrado em Engenharia de Produção), Escola de Engenharia, Universidade Federal do Rio Grande do Sul, Porto Alegre, 2014.

STAUDT, F. H. Estudo de métodos de previsão de demanda com incorporação de julgamentos. 2011. 169p. Dissertação (Mestrado em Engenharia de Produção), Universidade Federal de Santa Catarina, Florianópolis, 2011.

WEBBY, R.; O'CONNOR, M. Judgement and Statistical Time Series Forecasting: a Review of the Literature. International Journal of Forecasting, v.12, p.91-118, 1996.

WEBBY, R.; O'CONNOR, M.; LAWRENCE, M. Judgmental Time-Series Forecasting Using Domain Knowledge. In: ARMSTRONG, J. S. Principles of Forecasting: A Handbook for Researchers and Practitioners. Kluwer Academic Publishers. 2001.

WERNER, L. Um Modelo Composto para Realizar Previsão de Demanda através da Integração da Combinação e de Previsões e Ajuste Baseado na Opinião. Tese de Doutorado. Universidade Federal do Rio Grande do Sul, Porto Alegre, 2004.

WERNER, L.; RIBEIRO, J. L. D. Modelo composto para prever demanda através da integração de previsões. Produção, v. 16, n.3, p.493-509, 2006.

WRIGHT, G. LAWRENCE, M. J.; COLLOPY, F. The Role and Validity of Judgement in Forecasting. International Journal of Forecasting, v.12, 1996, p.1-8.

1. Universidade Federal do Rio Grande do Sul - UFRGS, Brasil, rodolfoengenheiro@hotmail.com
2. Universidade Federal do Rio Grande do Sul - UFRGS, Brasil, liane@producao.ufrgs.br