Espacios. Vol. 36 (Nº 08) Año 2015. Pág. 10
Fractais, contextualização de matemática e arte
Fractals, contextualization of Mathematics and Art
Simone SEMMER; Sani de Carvalho Rutz da SILVA 1; Marcos Cesar Danhoni NEVES; Luiz Alberto PILATTI
Recibido: 22/01/15 • Aprobado: 16/02/2015
Contenido
RESUMO: |
ABSTRACT: |
1. Introdução
Aliando razão e sensibilidade no ensino é possível, segundo Fainguelernt e Nunes (2006) observar a influência mútua entre duas áreas de conhecimento aparentemente antagônicas, mas que, quando intimamente ligadas podem fornecer em várias conexões, subsídios de investigação e reflexão. Assim, se definem estudos envolvendo Matemática e Arte.
Entre diversas conexões envolvendo Matemática e Arte, encontra-se atualmente o estudo dos fractais.
Do ponto de vista da Arte, os fractais além de revelarem belíssimas imagens, suas aplicações vão desde padronagens em tecidos, até o uso em cenas cinematográficas. E, no que diz respeito aos fractais na Matemática, estudam-se o crescimento e a complexidade da natureza, por meio de uma linguagem que descreve, analisa e modela as formas encontradas, denominada Geometria Fractal. O documentário: Fractais, uma jornada pela dimensão oculta (DUETTO, 2009) mostra além de aplicações em Arte e em Matemática, seus empregos em Economia, Medicina, Biologia e Física, relatando um breve histórico da teoria dos fractais e do avanço de pesquisas nas diversas áreas.
Relativos aos avanços das pesquisas de Geometria Fractal, seu ensino nas escolas tem sido motivado pela amplitude de metodologias que podem ser usadas. Podendo contextualizá-lo tanto com recortes de papel, quanto com softwares de geometria dinâmica. Exemplos metodológicos podem ser encontrados em Brandão (2002), Frame e Mandelbrot (2002), Barbosa (2002), Sallum (2005), Dias (2010) e Nascimento (2012), entre outros pesquisadores.
Cabe ressaltar ainda, os trabalhos de pesquisa de Baier (2005) e Chaves (2008), que relacionados a fractais, especificamente usaram Matemática e Arte.
Como exposto, especialmente em relação à Arte, imagens fractais geradas em ambientes informatizados são belíssimas e se tornam verdadeiras obras de arte, no entanto, a presença de fractais foi identificada em obras de arte realizadas antes dos avanços tecnológicos. Entre elas se destacam as de Leonardo da Vinci, Katsushika Hokusai e Maurits Cornelis Escher, que foram analisadas e descritas por Mandelbrot em The Fractal Geometry of Nature (1983) e em The Science of Fractal Images (1988). Da mesma forma, em obras de Jackson Pollock dimensões fractais foram identificadas por Taylor (2009) e, explicadas por Crato (2009).
Assim, por meio de obras de artistas, este artigo pretende apresentar e discutir a conexão Matemática e Arte, envolvendo fractais. Nele, estão descritas propriedades e características de fractais, bem como a descrição de análise de obras de arte envolvidas à luz da literatura e dos fundamentos matemáticos. Inova-se nesse texto, a presença de propriedades fractais na pintura de Salvador Dali intitulada O rosto da guerra. Este documento também sugere a utilização das análises aqui descritas para uso em sala de aula, revelando mais uma aplicação interdisciplinar de Geometria Fractal.
2. Fractais
Nas últimas décadas do século XX, viu-se o nascimento e desenvolvimento da ciência denominada Caos que trouxe consigo a observação de ordem e padrões em ambientes caóticos, irregulares, aleatórios e imprevisíveis. A Geometria dos fractais está intimamente ligada a esta ciência. Os objetos fractais, observáveis na natureza compõem suas formas onde dominam a irregularidade e o caos. São objetos fractais da natureza os mares e oceanos, continentes e ilhas, com suas costas, montanhas, rios e rochas, animais e plantas, e o céu com suas nuvens e raios. O universo inteiro pode ser descrito na forma fractualizada, até mesmo as galáxias (BARBOSA, 2002).
Segundo Barbosa (2002) Benoit Mandelbrot (1924-2010) criou a denominação "fractais" ao empregar situações e modelos de outros cientistas à resolução de problemas. Dentre os diversos modelos e situações fractais, que podem ser usados em sala de aula, destacam-se na literatura, os fractais Poeira de Cantor, Triângulo e Tapete de Sierpinski, Conjunto de Julia, Curva e Ilha de Koch, Curva de Hilbert e Curva de Peano. Tais indicações didáticas se encontram em Frame e Mandelbrot (2002), Barbosa (2002), Sallum (2005) e Dias (2010).
Em sala de aula os fractais podem ser usados para ensinar vários conteúdos, como explica Sallum (2005, p. 1):
A introdução de fractais no ensino médio, além de satisfazer a curiosidade de quanto já ouviram falar neles, propicia a oportunidade de trabalhar com processos iterativos, escrever fórmulas gerais, criar algoritmos, calcular áreas e perímetros de figuras com complexidade crescente, introduzir uma ideia intuitiva do conceito de limite e é um excelente tópico para aplicação de progressões geométricas e estímulo ao uso de tabelas.
Como explica o autor, o uso de tabelas e as Progressões Geométricas pode ser uma metodologia excelente usando os fractais. O fractal ao ser construído modifica a sua forma segundo uma sequência lógica, e esta sequência possui estágios de desenvolvimento numerados consecutivamente.
Ao se tratar do fractal Curva de Koch (figura 1), por exemplo, o estágio 0 ou semente é uma linha ou reta AB. Seu estágio 1 "é uma curva que vai do ponto A ao ponto B, formada por 4 segmentos de mesmo comprimento, igual a um terço (⅓) da distância de A até B" (SALLUM, 2005, p. 1). Os estágios subsequentes repetem a mesma curva, em cada segmento da figura inicial, sempre reduzindo a terça parte (⅓) de seu tamanho, até formar uma nova curva de A até B. No estágio 2 por exemplo, a curva será formada por 16 segmentos, no estágio 3, terá 64 segmentos, formando assim, uma Progressão Geométrica nos números de segmentos formados.
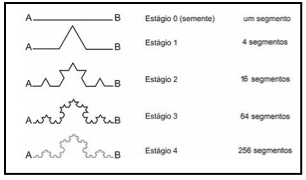
Figura 1 - Curva de Koch.
Fonte: Adaptado de Kinouchi in www.ceticismoaberto.com/ciencia/kinouchi_frac (2006)
Pode-se repetir o padrão escolhido em ambiente informatizado por diversas vezes, infinitamente. Em sala de aula, segundo Sallum (2005), é importante colocar os dados em um quadro e realizar a generalização, encontrando assim uma lei de formação da progressão, podendo calcular o número de segmentos para qualquer estágio de desenvolvimento.
No quadro 1 pode-se observar que na Curva de Koch existem dois tipos de Progressões Geométricas. Uma crescente de razão 4, em relação ao número de segmentos e outra decrescente, de razão ⅓ ou 3-1 em relação à medida de cada segmento. A lei de formação do perímetro da Curva de Koch mostra a tendência ao infinito, assim como a medida e a quantidade de segmentos.
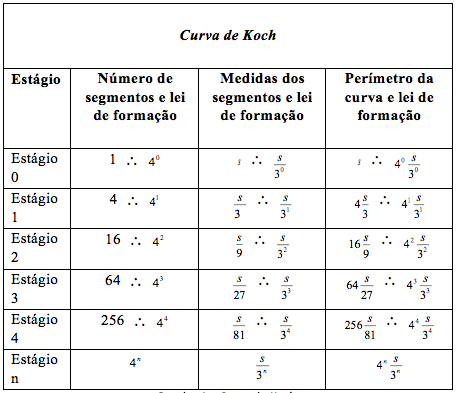
Quadro 1 – Curva de Koch.
Fonte: Adaptado de Sallum (2005)
Também se pode verificar que na última curva da ilustração (estágio 4, figura 1) há partes da linha que se assemelham à cópia do todo, pois a cada estágio de desenvolvimento, repete-se a mesma operação (figura 2). Autosimilaridade é o nome dessa propriedade.
A autosimilaridade apresenta-se como uma propriedade notável dos fractais, a imagem apresenta seus padrões característicos repetidamente encontrados em escala decrescente, de modo que suas partes, em qualquer escala, são, na forma, semelhantes ao todo (CAPRA, 2006).
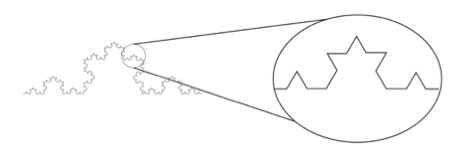
Figura 2 – Autosimilaridade da Curva de Koch.
Fonte: adaptado de Kinouchi in www.ceticismoaberto.com/ciencia/kinouchi_frac, 2006
A autosimilaridade é explicada por Stewart (1991, p. 234) como sendo a exibição da estrutura detalhada ao longo de muitas escalas. Um "fractal matemático ideal tem estrutura numa série infinita de escalas". Ou seja, um fractal possui duas características fundamentais, a autosimilaridade e a tendência ao infinito.
Como visto anteriormente, quando se refere às formas da natureza, a Geometria Fractal descreve, analisa e modela essas formas por meio de linguagem matemática. Mandelbrot (1998, p. 13), afirma que fractal "surge a partir do adjetivo latino fractus, que significa irregular ou quebrado". É uma geometria de rara beleza que pode ser visualizada por meio dos recursos computacionais existentes.
O mais famoso fractal é o Conjunto de Mandelbrot cuja imagem provém da equação z2 + c, onde z e c são números complexos. Sua resolução é explicada por Horgan (2009, p. 8-9):
Com um valor fixo para c, e z sendo zero, calcula-se o resultado. A seguir, calcula-se repetidamente, ou itera-se a equação, substituindo cada novo resultado por z. Alguns valores de c, quando colocados nessa função iterativa, produzem resultados que rapidamente disparam para o infinito. Outros valores de c produzem resultados que oscilam rápida e eternamente dentro de certos limites.
O Conjunto de Mandelbrot quando visualizado, segundo Horgan (2009, p. 8), a imagem não possui as bordas lisas, mas semelhantes a chamas, a "amplificação repetida das bordas nos leva a um padrão fantasmagórico sem fim de imagens barrocas".
Capra (2006, p. 128) descreve o Conjunto de Mandelbrot como um "armazém de padrões de detalhes e de variações infinitas". Segundo o autor (2006, p. 126), esse fractal apresenta "espirais dentro de espirais, cavalos marinhos e vórtices, repetindo incessantemente os mesmos padrões".
É possível visualizar esse e outros fractais por meio de software livre denominado Xaos (1996), que permite ampliar e deslocar um fractal em tempo real, exibindo as imagens rapidamente. Esse software, além de outras funções, permite ver a imagem de um fractal modicando uma forma inicial e gerando iterações para se transformar em fractal. A imagem é gerada infinitamente, destacando a autosimilaridade das formas fractais.
Utilizar a autosimilaridade e a tendência ao infinito do fractal Triângulo de Sierpinski, por exemplo, pode ser uma forma contextualizada de aplicação dos conteúdos de Geometria Plana e das Progressões Geométricas (BARBOSA, 2002).
No Triângulo de Sierpinski (quadro 2) os estágios iniciam com um triângulo equilátero, dividido em quatro triângulos congruentes proporcionais ao original na razão de semelhança igual a 2-1 (½) . Em seguida, retira-se o triângulo central, reduzindo o triângulo original em um quarto (¼) de sua área. Aos triângulos restantes, no estágio seguinte, repete-se a divisão em quatro triângulos, e a retirada do triângulo central.
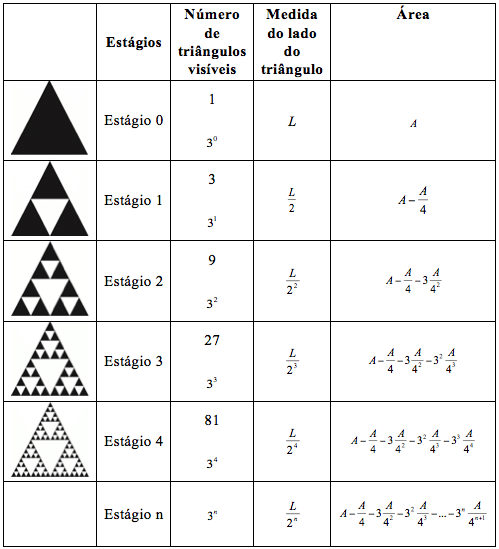
Quadro 2 - Triângulo de Sierpinski.
Fonte: adaptado de Kinouchi in www.ceticismoaberto.com/ciencia/kinouchi_frac, 2006
Repetindo-se infinitamente o processo, tem-se uma estrutura fractal (quadro 2). As generalizações quanto ao número de triângulos visíveis mostra a configuração de uma Progressão Geométrica crescente de razão 3. Quanto à medida do lado de cada triângulo, a Progressão Geométrica apresenta-se decrescente, de razão ½ ou 2-1 e, a generalização da área, mostra sua tendência a zero (0), na medida em que da área inicial A são retirados os triângulos, que se apresentam cada vez menores e em maior quantidade.
Nesta mesma concepção de exemplos, Frame e Mandelbrot (2002), Sallum (2005) e Barbosa (2002) indicam outros fractais a serem usados na sala de aula. Os autores, além de explicar a autosimilaridade e a tendência ao infinito também explicam a dimensão fractal.
Para se calcular a dimensão fractal é necessário entender a dimensão euclidiana, que estabelece as configurações d = 0 para o ponto, d = 1 para a linha, d = 2 para o plano e d= 3 para figuras geométricas espaciais (figura 3).
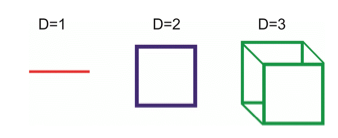
Figura 3 - Dimensões euclidianas.
Fonte: Adaptado de http://www.absoluteastronomy.com/topics/Fractal_dimension
Os fractais se distinguem do espaço euclidiano por estabelecerem dimensões de caráter irracional (0 < d < 1; 1 < d < 2; 2 < d < 3) e, são determinados por meio de uma expressão logarítmica: ![]() , em que m representa o número de segmentos semelhantes e n, a razão de semelhança.
, em que m representa o número de segmentos semelhantes e n, a razão de semelhança.
Essa expressão segundo Nascimento (2012), pode ser usada para encontrar dimensões como dos fractais Curva de Koch e Triângulo de Sierpinski, pois apresentam autosemelhança exata.
No fractal Curva de Koch, por exemplo, Sallum (2005, p. 2) explica que "a cada etapa de construção acrescentam-se quatro cópias reduzidas da etapa anterior", então, o número de segmentos desse fractal é 4, logo, m = 4. E, nesse mesmo fractal, a cada etapa de construção, a cada estágio de desenvolvimento, os segmentos se reduzem a ⅓ do tamanho anterior, portanto, a razão de semelhança é n = 3.
Aplicando esses dados na expressão tem-se ![]() , logo, a dimensão do fractal Curva de Koch é d = 1,26.
, logo, a dimensão do fractal Curva de Koch é d = 1,26.
Já a dimensão d do Triângulo de Sierpinski corresponde ao quociente logarítmico entre o número de triângulos resultantes a cada estágio (m = 3), e o coeficiente de redução da medida do lado do triângulo (n = 2), ou seja, ![]() . Isto é, para o Triângulo de Sierpinski a dimensão apresenta-se como d = 1,58.
. Isto é, para o Triângulo de Sierpinski a dimensão apresenta-se como d = 1,58.
Se a dimensão da Curva de Koch corresponde a 1,26 e, a do Triângulo de Sierpinski corresponde a 1,58, ambas correspondem à dimensões fractais, como se pode observar na figura 4 pois as dimensões estão compreendidas entre as dimensões euclidianas 1 e 2. Ou seja, 1 < 1,26 < 2 e 1 < 1,58 < 2.
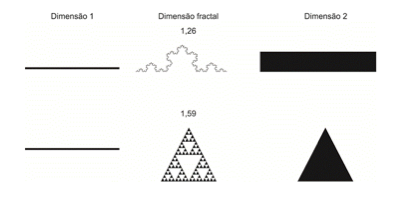
Figura 4 – Comparação de dimensões fractais.
Fonte: Adaptado de http://pages.uoregon.edu/msiuo/taylor/art/scientificamerican.pdf
Em resumo, de acordo com as informações descritas, os fractais distinguem-se por apresentar autosimilaridade, tendência ao infinito e dimensão irracional.
Diante dessas características dos fractais, segundo Mandelbrot (1983, 1988) existem obras de arte, descritas a seguir, cujas estruturas matemáticas de ordem, medidas e padrões se apresentam com autosimilaridade, tendência ao infinito e dimensão irracional, as quais podem apresentar composições que se remetem a estruturas fractais e, à Geometria Fractal.
3. Fractais e obras de arte
A Geometria Fractal de acordo com Barbosa (2002, p. 9) teve o seu "inegável apelo estético, daí sua entrada no domínio das artes". Essa Geometria trouxe a visualização de ordem e de padrões em situações em que somente se observava o irregular, aleatório e imprevisível, acrescentando assim, distintas formas de conceber o Universo. Mandelbrot (1998, p. 219) corrobora quando relata:
Retomando a ideia da linguagem, vemos que a geometria fractal vem acrescentar novos caracteres ao alfabeto que Galileu herdara de Euclides. Desde os tempos longínquos da descoberta da perspectiva que o homem da rua não via nada de semelhante sair da matemática e nem o próprio matemático alguma vez imaginara que o seu domínio poderia interagir desta forma com a arte.
Concordando com Barbosa e com Mandelbrot, e, buscando interagir Matemática e Arte, descreve-se a seguir as obras de Dalí, Hokusai, Escher e Pollock relacionando-as com as características dos fractais: a autosimilaridade, a tendência ao infinito e a dimensão fractal.
A escolha das obras deveu-se às indicações de Mandelbrot (1983, 1988) e de Crato (2009). As obras de arte de Hokusai, indicações de Mandelbrot (1983), enquanto que a dimensão fractal encontrada em obras de Pollock foram analisadas por Richard P. Taylor em pesquisa sobre caos e fractais (CRATO, 2009). No que diz respeito aos círculos e quadrados infinitos de Escher, Mandelbrot os explicou em The Science of Fractal Images (1988) e, Ernst em O Espelho Mágico de M. C. Escher (2007). E, em se tratando de uma sucessão de imagens semelhantes em escala tendendo ao infinito, exemplifica-se com uma tela de Dalí (RIUS, 2007).
A seguir, detalham-se cada obra nas especificidades em relação à Arte e à concepção de fractais.
Conhecido por suas gravuras retratando o monte Fuji, Katsushika Hokusai (1760-1849) realizou composições que retratam a natureza cujas repetições ordenadas sugerem composições fractais. Mandelbrot citou Hokusai com a obra A grande onda de Kanagawa (figura 5) em The Fractal Geometry of Nature (1983) como utilizador de Geometria Fractal nas suas gravuras.
No documentário Fractais: uma jornada pela dimensão oculta, citado anteriormente, Mandelbrot afirma que depois que citou Hokusai, muitos lhe disseram que conseguiam compreender as gravuras e as imagens retratadas pelo artista japonês. Ele, de certa forma antecipou o uso das características fractais descritas somente no século XX. Kaye (1989) ao descrever a teoria do Caos ligada à turbulências, cita Both Kadanoff e Mandelbrot que discutem a turbulência da famosa gravura japonesa que mostra os fractais das ondas numa repetição de formas.

Figura 5 - A grande onda de Kanagawa. (Gravura 25 x 37 cm)
Fonte: MANDELBROT 1983
As diversas obras dos séculos XVIII e XIX de Hokusai mostram a concepção fractal do artista nas repetições dos fragmentos das ondas e das nuvens, imagens claras da natureza representadas detalhadamente. "Assim, a propriedade de escala que caracteriza os fractais não está presente só na natureza, mas em algumas das criações mais cuidadosas do homem" (MANDELBROT, 1983, p. C16).
A escala foi usada por Maurits Cornelis Escher (1898-1972) que é referência obrigatória, segundo Fainguelenrt e Nunes (2006), quando se exprimem artistas que se utilizaram da Matemática para compor suas obras. Escher conseguiu de forma consciente, inserir conceitos matemáticos com uma notável combinação de sensibilidade e precisão. Em diversos períodos da sua vida, segundo Ernest (2007), Escher utilizou conceitos matemáticos de Möbius, Poincaré, Riemann e Penrose para compor suas obras.
Escher tinha o desejo de penetrar nas profundezas do infinito, de se aproximar dele, e expressá-lo com a ajuda de imagens estáticas, perceptíveis sobre o papel. Segundo Ernst (2007), o artista também tinha a noção de que é impossível produzir uma superfície que se estende infinitamente em todas as direções, mas que poderia dar noção de infinito. A respeito de suas obras, Escher, em seus comentários explica que "quem quiser representar um número infinito, tem que reduzir gradualmente o tamanho das figuras até que alcance, pelo menos teoricamente, o limite do formato infinitamente pequeno" (ESCHER, 2004, p. 10).
Quanto às orientações visuais do artista em relação ao infinito, Ernst dedica o último capítulo de O Espelho Mágico de M. C. Escher (2007) para explicar que Escher trabalhou basicamente com duas formas de expressar o infinito numa figura plana, sendo da extremidade ao centro, ou do centro à extremidade, indiferentemente se realizada com círculo ou quadrado.
Observa-se que as obras de Escher (figuras 6 e 7) tendem ao infinito, nelas, há relações matemáticas como perspectiva, uso de padrões e simetrias e, escalas. Em seus esboços é possível ver linhas implícitas, diagramas e representações gráficas indicando relações matemáticas existentes, como se observa no esquema da figura 7.

Figura 6 - Limite circular I, 1958
Xilogravura, diâmetro de 42 cm
Fonte: VEDHUYSEN, 2006
----
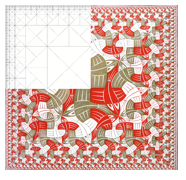
Figura 7 - Limite Quadrado, 1964
Xilogravura, 34 x 34 cm
Fonte: VEDHUYSEN, 2006
Tomando como exemplo a tesselação de lagartos de um esboço de Escher (figura 8) divulgado por Vedhuysen (2006), verifica-se que os elementos figurativos - os lagartos – seguem uma sequência de escalas de tamanhos a qual pode ser visualizada com a malha de triângulos sobreposta na composição (figura 9).
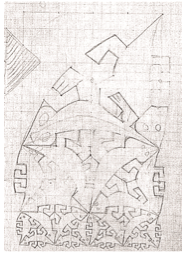
Figura 8 – Esboço de Escher (1964)
Fonte: VENDHUYSEN (2006, p. 68)
----
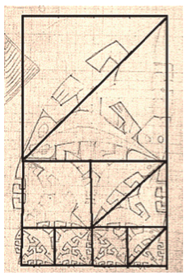
Figura 9 – Malha geométrica sobreposta à obra de Escher.
Fonte: Adaptado de VENDHUYSEN (2006, p. 68)
O esboço e as linhas de composição da imagem dele formam quadriláteros divididos em triângulos. Cada triângulo foi dividido na sua metade, então, o tamanho do triângulo imediatamente menor que o anterior fica reduzido à metade de sua área.
Quando se visualizam apenas alguns lagartos da imagem (figura 10), verifica-se uma sequência de escalas e Progressão Geométrica nos desenhos.

Figura 10 - Elementos figurativos do esboço de Escher, colocados em evidência.
Fonte: Adaptado de VEDHUYSEN (2006, p. 68)
Tomando como exemplo um esquema da figura 10, destacada no quadro 3, a Progressão Geométrica envolvida é decrescente de razão 2-1 em relação ao tamanho dos lagartos, mas crescente de razão 2 em relação ao número de lagartos desenhados em cada estágio, semelhanças essas com as leis de formação da Curva de Koch.
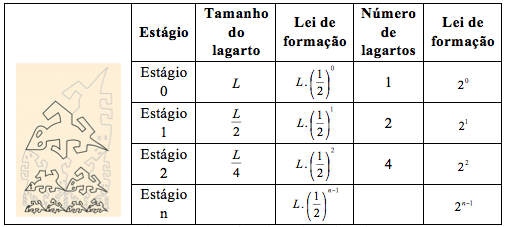
Quadro 3 – Estrutura fractal de esboço de Escher.
Fonte: Autoria própria
Diante do quadro 3, no comparativo de formas em escalas usado por Escher, pode-se configurar a análise visual de que há conceitos fractais na imagem do esboço desse quadro, tanto na repetição de elementos em escalas, como na tendência ao infinito das Progressões Geométricas analisadas.
Ou seja, nos esboços de Escher os detalhes, peculiaridades e irregularidades dos padrões geométricos são intimamente ligadas à Matemática (BARBOSA, 1993).
Contemporâneo a Escher, Salvador Felipe Jacinto Dalí (1904-1989) foi descrito por Fainguelernt e Nunes (2006) como um artista contemporâneo polêmico, brilhante, versátil e significativo. Além de pintor, foi escritor, escultor, designer de joias, ilustrador e coreógrafo. Ao transitar entre várias correntes artísticas, destacou-se mais no Surrealismo. De acordo com as autoras, é possível explorar conceitos matemáticos como simetria, perspectiva, profundidade, secção áurea e proporção nas obras de Dalí. O Rosto da Guerra, (figura 11), mostra uma repetição de crânios humanos, em escalas menores, e tendendo ao infinito.

Figura 11 – O rosto da guerra, 1940-1941. Óleo sobre tela 66 x 79 cm
Fonte: RIUS, 2007
Descharnes e Néret (1997), afirmam que, dentre as três inspirações do artista, a angústia da morte é um deles, sendo a libido e o instinto sexual as outras. Para compor a obra de 1941, o artista espanhol se encontrava nos Estados Unidos, num período marcado pelo pós-guerra espanhol, e, durante a Segunda Guerra Mundial. Segundo Rius (2007, p. 64) ao fazer essa obra, o artista estava em intenso processo criativo, em que as imagens vividas pelos horrores da guerra impregnavam suas composições. O autor descreve a tela O rosto da guerra como "uma grande caveira", em cujos "olhos e boca se reproduzem mais caveiras". Dentro dessas, outras caveiras, na mesma razão de repetição, "criando uma percepção infinita de morte e desolação". Ainda, o autor complementa, se referindo à obra, afirmando que "a fórmula empregada é quase matemática, para tentar descrever um fenômeno complexo, que seria inexplicável por meio de métodos tradicionais".
Como se pode observar no quadro 4, de acordo com o exposto, a obra de Dalí mostra uma repetição de imagens em escalas, a parte se assemelha ao todo, e apesar do suporte – a tela – não conceder o infinito, ele pode ser visualizado na repetição ordenada em que os espaços vazios da boca e dos olhos da caveira refletem novas caveiras, em tamanho menor, e seu número em Progressão Geométrica de razão 3, simulando o infinito na escala usada (quadro 4). Quando se referem à imagem como um todo, Descharnes e Néret (1997, p. 389), a descrevem como "a horrível figura da guerra, os olhos repletos de morte infinita". O infinito também pode ser observado na proporção em que cada caveira se apresenta em menor tamanho, mas em maior quantidade, assemelhando-se ao observado no Triângulo de Sierpinski.
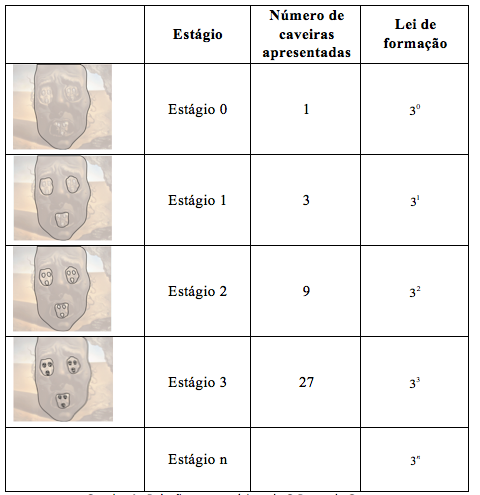
Quadro 4 - Relações matemáticas de O Rosto da Guerra.
Fonte: Autoria própria
Salvador Dalí compôs obras polêmicas durante quase toda a sua vida, algumas delas, repletas de Matemática, em que usou perspectiva, introduziu proporção áurea, e simetrias nas mais diversas variações, além de compor proporções tendendo ao infinito. Fainguelernt e Nunes (2006) apresentam uma série de atividades utilizando as obras de Dalí, mas não citam O Rosto da Guerra, nem a visualização de fractais, no entanto, no que diz respeito às propriedades dos fractais, - a autosimilaridade e a tendência ao infinito - a obra pode ajustar-se perfeitamente.
No contexto do estudo de fractais, Taylor (DUETTO, 2009) tem pesquisado a dimensão fractal em obras de Jackson Pollock (1912-1956), que numa combinação de traços coloridos ritmados, pingos de tinta e espirais extensas sobre gigantescas lonas, compôs uma série inovadora para os anos 40/50 do século XX.
Ao ser observado na ênfase de uma composição, Pollock segundo Crato (2009), começou a dar voltas no quadro (uma lona esticada no chão de um celeiro, ateliê do artista), e em cada volta que dava, sua inquietação era visível. Até que, subitamente parou, e, com um balde de tinta, começou a borrifar o quadro na horizontal, deixando a força da gravidade atuar sobre a tinta.
Nessa composição, como se pode observar na figura 12, Pollock pintava-o por camadas, de início, grossas, usando uma cor base. Em seguida, traços mais finos, em longos movimentos de braço, como nos riscos de tinta e salpicos. Ao final, usava movimentos mais curtos, finos riscos e pequenos pingos, um processo complexo e sem arbitrariedade (CRATO, 2009).

Figura 12 - Reflexão da Ursa maior 1947. Óleo sobre tela 111 x 95 cm
Fonte: http://www.ocaiw.com/catalog/?lang=pt&catalog=pitt&author=592
Não sabia Pollock, de acordo com Crato (2009), que sua composição seria analisada por cientistas. O físico Richard Taylor analisou obras de Pollock e as conceituou como aproximações de imagens da natureza, numa formação remetendo a processos caóticos que produzem fractais. A atuação do processo é "semelhante com o que acontece com a natureza, que salpica as paisagens de relevo e vegetação" (p. 131).
Taylor simulou a pintura de Pollock e pode comparar o resultado à dimensão fractal resultante e, analisou as obras do período de 1943 a 1952. Ele concluiu que o artista americano foi explorando sucessivamente a complexidade de suas pinturas. As telas de 1943 possuem dimensão pouco superior a 1, as de 1947 (figura 12), dimensão 1,45 – valor estimado para estruturas da natureza - e a obra de 1952, com 1,72 de dimensão fractal (CRATO, 2009).
As imagens do experimento de Taylor mostram as dimensões numa escala crescente da dimensão 1 até a dimensão 2, passando pelas dimensões fractais, segundo um esquema gráfico (figura 13).

Figura 13 – Esquema gráfico de dimensões.
Fonte: Adaptado de http://pages.uoregon.edu/msiuo/taylor/art/scientificamerican.pdf
Portanto, diante do esquema e das pesquisas de Taylor, pode-se dizer que as obras de Pollock oscilaram sua dimensão d entre dimensões euclidianas de 1 e 2, classificando-as como dimensões não-euclidianas, dimensões fractais, ou seja, 1 < d < 2.
Assim, mediante o exposto, configuram-se conexões em Arte e Matemática relativas aos fractais, usando obras de arte. No que diz respeito às propriedades de Geometria Fractal pode-se dizer que são visualizadas em obras de vários artistas, mesmo entre os que viveram numa época distante de formulações dessa Geometria.
De toda forma, a ideia de fractais incorporados às obras de arte não configuram que os artistas as tenham usado. Mas, são percebidas e podem ser aproveitadas para auxiliar a visualização da Geometria da -Natureza e do Universo.
Considerações finais
Uma conexão de Matemática e Arte envolvendo a Geometria Fractal foi apresentada e discutida por meio de obras de arte, mostrando algumas relações existentes.
Pode-se observar a presença de propriedades fractais em obras de Salvador Dalí, Maurits C. Escher, Katsushika Hokusai e Jackson Pollock. As obras distinguem-se nas composições e na exploração de Geometria Fractal, entretanto o conjunto delas pode propiciar um novo olhar sobre a cultura matemática existente.
Entende-se que para a utilização desse tipo de visualização em aulas de Matemática, é necessário que o professor dessa disciplina se interesse pelo assunto, e perceba as conexões interdisciplinares. No entanto, a articulação entre essas duas áreas do conhecimento, pode propiciar não só o uso de saberes matemáticos no contexto artístico, mas um entendimento de cultura, de aplicações de uma nova linguagem geométrica, que não se apresenta totalmente nova, mas que inspiram a utilizá-la de forma inovadora.
Como sugestão, poderiam tanto professores de Arte como professores de Matemática, trabalhar Fractais de formas distintas, mas articuladas tanto pelo apelo estético quanto pela composição geométrica.
Referências
BAIER, Tania. O nexo "geometria fractal – produção da ciência contemporânea" tomado como núcleo do currículo de matemática do ensino básico. 2005. 147 f. Tese (Doutorado em Educação Matemática). Universidade Estadual Paulista, Rio Claro, SP. 2005. Disponível em:<http://www.athena.biblioteca.unesp.br/exlibris/bd/brc/33004137031P7/2005/baier_t_dr_rcla.pdf>. Acesso em: 12 set. 2011.
BARBOSA, Ruy Madsen. Descobrindo padrões em mosaicos. São Paulo: Atual, 1993.
___________. Descobrindo a Geometria Fractal para a sala de aula. Coleção Tendências da Educação Matemática. Belo Horizonte: Autêntica, 2002.
BRANDÃO, Leônidas de Oliveira. Algoritmos e fractais com programas de GD. Revista do Professor de Matemática. 49, 2002.
[5] CAPRA, Fritjof. A teia da vida. São Paulo: Cultrix, 2006.
CHAVES, Márcia de Nazaré Jares Alves. "Sentimento de semelhança": poéticas visuais de interconexões em arte e matemática. 2008. 127 f. Dissertação (Mestrado em Educação em Matemática) Universidade Federal do Pará. Belém, PA. 2008. Disponível em: <http://bc.ufpa.br/Portal/DTD/Escola_de_Aplicacao/Escola_de_Aplicacao_2008/CHAVES.htm>. Acesso em: 11 set. 2011.
CRATO, Nuno. A Matemática das Coisas, do papel A4 aos cordões de sapatos, do GPS às rodas dentadas. São Paulo: Livraria da Física, 2009.
DESCHARNES, Robert ; NÉRET, Gilles. Salvador Dalí, 1904-1989. Taschen, 1997.
DIAS, Ana Lucia Braz. O fractal de Grossman. Revista do professor de matemática, 72, 2010.
DUETTO. Fractais: uma jornada pela dimensão oculta (documentário). Scientific American Brasil, 2009a.
___________. Fractais: uma jornada pela dimensão oculta. Edição temática. Scientific American Brasil. 2009b.
ERNST, Bruno. O Espelho Mágico de Escher. Taschen, 2007.
ESCHER, Maurits Cornelis. Gravuras e Desenhos. Taschen, 2004.
FAINGUELERNT, Estela Kaufman, NUNES, Regina Ashton. Fazendo arte com a matemática. Porto alegre: Artmed, 2006.
FRAME, M. L.; MANDELBROT, B. B. Fractals, graphics, & mathematics education. Washington: MAA, 2002.
KAYE, Brian H. A random walk through fractal dimensions. Cambridge – New York: VCH, 1989.
MANDELBROT, Benôit. The fractal geometry of nature. New York: Freeman, 1983.
___________. The prehistory of some fractals-to-be: Poincaré, Fricke, Klein and Escher. in Barnsley, M. F. et all. The science of fractal images. New York: Springer-verlag, 1988.
___________. Objectos Fractais. Lisboa: Gradiva, 1998.
NASCIMENTO, Maristel do. Uma proposta metodológica para o ensino de geometria fractal em sala na educação básica. 2012. 87 f. Dissertação (Mestrado em Ensino de Ciência e Tecnologia) – Programa de Pós-Graduação em Ensino de Ciência e Tecnologia, Universidade Tecnológica Federal do Paraná. Ponta Grossa, 2012.
SALLUM, Élvia Mureb. Fractais no ensino médio. Revista do professor de matemática, 57, 2005.
STEWART, Ian. Será que Deus joga dados? A nova matemática do caos. Rio de janeiro: Jorge Zahar, 1991.
RIUS, Josep. Salvador Dalí. Coleção Folha, Grandes Mestres da Pintura. Barueri-SP: Editorial Sol 90, 2007.
TAYLOR, Richard P. Ordem no caos de Jackson Pollock. in DUETTO. Fractais:uma jornada pela dimensão oculta (documentário). Scientific American Brasil, 2009a. Disponível em: < pages.uoregon.edu/.../taylor/.../scientificamerican>. Acesso em 23 mai. 2010.
VEDHUYSEN, W. F. The magic of M. C. Escher. London: Thames & Hudson, 2006.
XAOS, Tutorial, 1996. Disponível em: <http://xaos.sourceforge.net/black/tutorial.html> . Acesso em 28 abr. 2013.
1. Professor do Programa de Pós-Graduação em Ensino de Ciência e Tecnologia - Mestrado Profissional e Doutorado Universidade Tecnológica Federal do Paraná - UTFPR (sanirutz@gmail.com)