Espacios. Vol. 35 (Nº 12) Año 2014. Pág. 14
Análise da Série de Retornos do Índice Bovespa utilizando como instrumental modelos Box-Jenkins
Analysis of Series of Returns Bovespa Index using as instrumental Box-Jenkins models
Raphael Silveira AMARO 1, Adriano Mendonça SOUZA 2
Recibido: 07/08/14 • Aprobado: 19/10/14
Contenido
|
RESUMO: Com o intuito de servir como um instrumental para que os investidores consigam reduzir de forma significativa o risco inerente aos investimentos no mercado de capitais brasileiro, tem-se como objetivo analisar o comportamento da série de retornos diários do Índice Bovespa, no período de 02 de janeiro a 07 de julho de 2014, e apontar um método alternativo de acompanhamento de tendências futuras. Para isto, utilizou-se a metodologia Box-Jenkins e, através dela, conseguiu-se identificar um modelo MA(2) que capturou de forma eficiente e significativa o comportamento da série em estudo, proporcionando aos investidores um auxílio a mais nas tomadas de decisões. |
ABSTRACT: In order to serve as a tool for investors to be able to significantly reduce the risk inherent in investments in the Brazilian capital market has to analyze the behavior of the series of daily returns of the Bovespa Index, between 02 January to July 7, 2014, and point out an alternative method for monitoring future trends. For this, we used the Box-Jenkins methodology and, through it, we were able to identify a MA (2) model that captured efficiently and significantly the behavior of the series under study, providing investors an aid in making the most decisions. |
1. Introdução
O Produto Interno Bruto (PIB) brasileiro, que representa a soma de todos os bens e serviços finais produzidos no país, apresentou uma expansão média de 4,57% ao ano [3] no governo Lula, entre os anos de 2003 a 2010. Este crescimento contribuiu para que, em 2011, o Brasil assumisse a sexta posição no ranking das maiores economias do mundo. Já nos anos subsequentes, de 2011 a 2013, percebemos que o PIB brasileiro continuou se expandindo, porém a uma taxa de crescimento menor que a expansão média vista no governo Lula.
Dentro da doutrina econômica, quando se alega que o PIB de um país está se expandindo, pressupõe-se que este país está aumentando a sua produção, isto é, em outras palavras, as suas empresas estão crescendo, levando a um aumento da oferta de emprego e, consequentemente, a um aumento da renda das famílias. Portanto, supõe-se que a expansão do Brasil nos últimos anos acarretou um aumento significativo da riqueza das famílias brasileiras.
Nota-se que, conforme a renda familiar aumenta, segundo Keynes (1936), o consumo familiar também se eleva, porém não na mesma proporção que o crescimento da renda, ou seja, somente uma parte deste aumento é consumido, a outra parte é poupada. Percebe-se a veracidade deste conceito quando se analisam os dados referentes ao saldo da caderneta de poupança dos brasileiros, nos anos de 2003 a 2013, e se depara com uma taxa média de crescimento de 14,95% ao ano [4] deste saldo neste período, indicando que parte do aumento da renda familiar do brasileiro está sendo poupado e aplicado na caderneta de poupança.
Porém, não seria mais vantajoso para o brasileiro investir as suas economias em algo talvez mais arriscado, porém com um potencial de rendimento mais elevado, como o mercado acionário? Imagina-se que muitas pessoas, por possuírem aversão ao risco, responderiam a esta pergunta com um taxativo "Não!", principalmente por considerarem o mercado acionário como um investimento de extremo risco, pois ele possui uma rentabilidade totalmente aleatória, que não pode ser antecipadamente conhecida ao certo.
Em parte concorda-se com essa aversão, porém, ver-se-á, através desta pesquisa, que os indivíduos conseguem reduzir o risco dos investimentos em ações através de técnicas estatísticas, pois, embora estes ativos possuam uma rentabilidade aleatória, é possível sim prever a tendência do seu preço futuro por meio de técnicas de previsão sedimentas na literatura.
O objetivo desta pesquisa é analisar o comportamento do Índice Bovespa [5] com o intuito de identificar um modelo, por meio da metodologia Box-Jenkins, que possa servir para auxiliar na tentativa de minimizar os riscos inerentes dos investimentos no mercado acionário brasileiro, pois a rentabilidade que este mercado pode proporcionar é extremamente significativa, levando o indivíduo a maximizar a sua satisfação em poupar com o intuito de aumentar, futuramente, o seu poder aquisitivo.
Devido à importância deste tema, existem inúmeros estudos realizados sobre o comportamento de ativos financeiros, como exemplo podemos citar: Araujo. et al. (2013), que aplicaram a metodologia Box-Jenkins nas ações das empresas mais negociadas da BM&FBOVESPA; Santos (2012), que analisou a série de preço de soja no norte do paraná através de modelos ARIMA; Leroy (2006), que realizou uma previsão do preço da Usiminas através da metodologia Box-Jenkins. Observe que, em todos estes estudos analisados, e também nesta pesquisa, a metodologia utilizada para modelagem da série financeira foi a metodologia Box-Jenkins.
A escolha do Índice Bovespa como o ativo financeiro deveu-se ao fato de que, este índice, segundo Piazza (2009), possui como característica principal medir a lucratividade de uma carteira hipotética, podendo, com isto, ser utilizado como parâmetro para calcular o rendimento que um investidor teria se possuísse as 100 ações com os maiores volumes de negociação dentro da BM&FBOVESPA [6].
O mercado acionário brasileiro possui vantagens incomparáveis em relação à rentabilidade de investimentos, porém este mercado possui um risco considerável e precisa da oferta de ferramentas que auxiliem a minimizá-los. Para tanto, é necessário existir um estudo que mostre técnicas estatísticas que possibilitem a um indivíduo prever com uma boa confiabilidade a tendência de um índice ou de um preço futuro de uma determinada ação negociada na bolsa de valores com o intuito de diminuir os riscos desta aplicação.
2. Metodologia
Neste item apresentam-se os aspectos metodológicos que nortearão esta pesquisa.
2.1 Base de dados
Os dados foram coletados no sitio da BM&FBOVESPA [7] e correspondem a informações diárias, no período entre 14 de março de 2014 a 07 de julho de 2014, do preço de fechamento, em pontos, do índice Bovespa (Ibovespa). Este índice, por sua vez, é considerado o indicador de performance mais importante da Bovespa, pois expressa o desempenho médio das cotações dos ativos de maior negociabilidade e representatividade dentro do mercado acionário brasileiro.
Este período, de 77 observações, foi escolhido pelo fato de que desde o início do ano de 2014 o Ibovespa vinha perdendo valor, dia após dia, e no dia 14 de março de 2014 foi observado o menor preço de fechamento do Ibovespa. Logo após este dia, o índice iniciou uma trajetória ascendente de valor, representando uma quebra estrutural, estabelecendo uma nova tendência de curto prazo para o ativo financeiro.
Observa-se que, as séries financeiras podem possuir características como: tendências, sazonalidades, pontos influentes, heterocedasticidade condicional e não-linearidade. Portanto, com o intuito de minimizar ou até mesmo eliminar algumas destas características, utilizou-se, nesta pesquisa, os retornos do Índice Bovespa, pois, segundo MORETTIN (2008), os retornos financeiros apresentam as seguintes características: 1) são, em geral, não-auto-correlacionados; 2) os quadrados dos retornos são auto-correlacionados; 3) estas séries apresentam agrupamentos de volatilidade ao longo do tempo; 4) a distribuição dos retornos apresenta caudas mais pesadas do que uma distribuição normal e, embora a distribuição seja aproximadamente assimétrica, ela é em geral leptocúrtica.
A série de retornos do Ibovespa pode ser calculada através da seguinte expressão matemática:
![]()
Em que, ![]() representa o preço de fechamento do Índice Bovespa em pontos.
representa o preço de fechamento do Índice Bovespa em pontos.
2.2 Abordagem conceitual
Ao se trabalhar com modelagem de séries temporais precisa-se, antes de mais nada, analisar se elas são estacionárias, isto é, em outras palavras, é necessário analisar os seus comportamentos para verificar se elas são geradas por processos estocásticos estacionários, pois, quando uma série temporal é dita não estacionária se torna impossível estimar todos os seus momentos, o que impossibilita a realização de inferências estatísticas sobre a série.
Existem vários testes com o intuito de verificar a estacionariedade de uma série temporal, porém, neste trabalho, utilizam-se o teste de Dickey Fuller Aumentado (DFA) e o teste de Kwiatkowski–Phillips–Schmidt–Shin (KPSS) [8].
Após a verificação de que a série em estudo é estacionária, pode-se começar a modelá-la através da metodologia ARIMA, também conhecida como Box-Jenkins. A ênfase desta metodologia, segundo GUJARATI (2006), está na análise das propriedades probabilística, ou estocásticas, das séries temporais segundo a filosofia de deixar que os dados falem por si, isto é, nesta metodologia, a variável dependente é explicada por seus valores passados e por seus termos de erro estocásticos.
Na prática, a modelagem de séries temporais pelo método Box-Jenkins é realizada em quatro etapas:
- Identificação: nesta etapa, encontram-se os filtros ARIMA e a ordem do modelo, representados pelos valores de
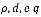 do modelo;
do modelo; - Estimação: logo após, estimam-se os parâmetros dos termos auto-regressivos e de médias móveis que serão incluídos no modelo, por meio do Método de Mínimos Quadrados – MMQ;
- Verificação: nesta fase, verifica-se se o modelo escolhido ajusta-se adequadamente aos dados, isto é, analisa-se se os resíduos estimados se comportam como um ruído branco [9], em caso positivo, passa-se para a quarta etapa, e em caso negativo, deve-se recomeçar;
- Previsão: esta é a fase final do processo, em que é estimada a previsão para a série temporal, em geral para um horizonte de curto prazo.
Entretanto, normalmente, quando se estudam as séries temporais financeiras se depara com um fenômeno peculiar denominado volatility clustering, mais conhecido na literatura brasileira como aglomeração de volatilidade. Quando se depara com esta peculiaridade, deve-se utilizar modelos da família ARCH (Autoregressive Conditional Heteroscedasticity) para modelar esta variância desigual da série, pois, conforme aponta GUJARATI (2006), a heterocedasticidade, ou variância desigual, pode ter uma estrutura auto-regressiva no sentido de que a heterocedasticidade observada ao longo de diferentes períodos pode ser autocorrelacionada.
Portanto, para verificar se a série em estudo possui heterocedasticidade, neste trabalho, aplica-se o teste ARCH-LM [10] nos resíduos quadráticos do modelo estimado pela metodologia ARIMA.
3 Evidências empíricas
Primeiramente, verifica-se se a série em estudo pode ser considerada um processo estocástico estacionário ou não. Para isto, antes de realizar os testes formais de estacionariedade, faz-se uma inspeção visual da série, conforme pode ser visto nas Figuras 1 e 2.
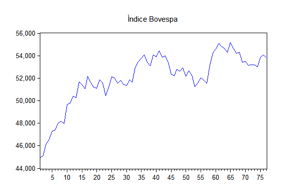
Fonte: BM&FBOVESPA;
Figura elaborada pelo autor.
Figura 1 - Série de pontos diários do Índice Bovespa, no período de 14 de março de 2014 a 07 de julho de 2014.
----

Fonte: BM&FBOVESPA;
Figura elaborada pelo autor.
Figura 2 - Série de retornos diários do Índice Bovespa, no período de 14 de março de 2014 a 07 de julho de 2014.
Observa-se que, na Figura 1, a série de pontos do Ibovespa apresentou uma tendência crescente, sugerindo que, talvez, a sua média tenha mudado ao longo do tempo, indicando a possibilidade da série ser não estacionária. Já na Figura 2, que representa a série de retornos do Ibovespa, não se pode identificar, somente com a análise visual, se a sua média, variância e autocovariância se mantiveram constantes ao longo do tempo.
Em continuidade com a inspeção visual da série de retornos do Ibovespa, utiliza-se a análise da sua Função de Auto-correlação (FAC) e de Auto-correlação Parcial (FACP), que pode ser visualizada na Figura 3.

Figura elaborada pelo autor.
Figura 3 – Função de Auto-correlação (FAC) e de Auto-correlação Parcial (FACP) da série de retornos do Índice Bovespa.
A análise da Função de Auto-correlação e da Função de Auto-correlação Parcial indica que a série em estudo parece ser estacionária, pois seus coeficientes de auto-correlação não se mostraram estatisticamente diferentes de zero. Porém, a inspeção visual de uma série temporal raramente permite distingui-la como de tendência estocástica ou determinística. E, frequentemente, quando se toma uma decisão apenas através da inspeção visual, incorre-se em equívocos. Portanto, necessita-se verificar a estacionariedade de uma série através de testes específicos de raiz unitária, como por exemplo o teste de Dickey Fuller Aumentado (DFA) e o teste de Kwiatkowski–Phillips–Schmidt–Shin (KPSS). Estes testes foram abordados na Tabela 1.
Tabela 1 – Testes de raiz unitária para a série de retornos do Ibovespa.
Variável |
ADF |
I(d) |
KPSS |
I(d) |
Retornos do Ibovespa |
-8.841622 |
I(0) |
0.391896 |
I(0) |
Fonte: Tabela elaborada pelo autor.
OBS: Os valores críticos para o teste ADF são: 1% -3.520307; 5% -2.900670; 10% -2.587691. Os valores críticos para o teste KPSS são: 1% 0.739000; 5% 0.463000; 10% 0.347000. Todos os testes foram realizados com interceptos e a série foi considerada em nível.
Percebe-se, na Tabela 1, que, os testes ADF e KPSS indicaram que a série de retornos do Índice Bovespa é estacionária e não contém raiz unitária ao nível de 5% de significância. Portanto, procede-se a pesquisa para a segunda etapa: encontrar um modelo matemático que seja representativo para a série em estudo. Para que isto aconteça, o resíduo deste modelo deve se comportar como ruído branco, ou seja, possuir média zero, variância constante e ser não correlacionado.
Dentre os vários modelos investigados, encontram-se cinco modelos que possuem esta característica nos resíduos. Estes modelos concorrentes para os retornos do Ibovespa e seus critérios de informação foram abordados na Tabela 2.
Tabela 2 - Modelos concorrentes para a série de retornos do Índice Bovespa.
Modelos |
Parâmetros |
Prob. |
AIC |
BIC |
AR(1) |
|
0.0099 |
6.069968 |
6.037590 |
MA(1) |
|
0.0114 |
6.063875 |
6.033208 |
MA(2) |
|
0.0000 0.0000 |
6.039537* |
5.978202* |
ARMA (1,1) |
|
0.0112 0.0615 |
6.074907 |
6.010150 |
ARMA(1,2) |
|
0.0000 0.0019 0.0466 |
6.146292 |
6.049157 |
Fonte: Tabela elaborada pelo autor.
Ao observar a Tabela 2, percebe-se que o melhor modelo para representar a série de retornos do Ibovespa é um MA(2), pois ele apresenta o menor AIC e o menor BIC entre os modelos concorrentes. A Figura 4 mostra a Função de Auto-correlação residual e a Função de Auto-correlação Parcial residual deste modelo, que evidenciam o comportamento de um ruído branco, pois os coeficientes de auto-correlação ficaram dentro dos limites de confiabilidade.

Figura elaborada pelo autor.
Figura 4 - Função de Auto-correlação residual e de Auto-correlação Parcial residual do modelo MA(2).
Portanto, o modelo mais adequado para realizar a modelagem da série pode ser descrito de acordo com a equação (1). Observa-se também, na Figura 5, a comparação entre o comportamento da série real e do modelo estimado.
![]()
(-9.605494) (4.844284)
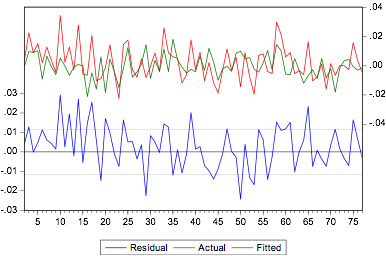
Figura 5 – Série de retornos do Ibovespa real em comparação com o modelo estimado e seu resíduo.
Vê-se, na Figura 5, que, o modelo escolhido, através da metodologia ARIMA, representou relativamente bem a série de retornos do Índice Bovespa para o período em análise. Entretanto, é preciso verificar se a sua variância condicional varia ao longo do tempo, ou seja, se a série apresenta heterocedasticidade condicional. Para isto, aplica-se o teste ARCH-LM nos resíduos quadráticos do modelo MA(2). O resultado deste teste pode ser visualizado na Tabela 3.
Tabela 3 – Resultado do teste ARCH-LM para os resíduos quadráticos do modelo escolhido.
Lags |
Estatística ARCH-LM |
Prob. |
Estatística F |
Prob. |
1 |
|
0.0525 |
3.886362 |
0.0525 |
2 |
|
0.0645 0.9775 |
1.876364 |
0.1607 |
Fonte: Tabela elaborada pelo autor.
Percebe-se, através da Tabela 3, que, não se pode aceitar a hipótese nula de inexistência de heterocedasticidade condicional na série de retornos do Ibovespa, ao nível de significância de 10%, mostrando que existe a necessidade de modelarmos a variação da variância no tempo. Portanto, sugere-se, para futuras pesquisas, que se utilizem modelos da família ARCH (Autoregressive Conditional Heteroscedasticity) para modelar a série do Ibovespa.
4 Conclusão
Este estudo teve como preocupação principal encontrar um modelo que explicasse de forma coerente as oscilações dos retornos do Índice Bovespa, com o intuito de servir como instrumental para que futuros investidores consigam investir seus recursos financeiros minimizando, da melhor maneira possível, o risco do mercado acionário brasileiro.
Portanto, o modelo encontrado, através da metodologia Box-Jenkins, que se mostrou mais adequado para análise da série de retornos do Índice Bovespa foi um MA(2). Entretanto, verificou-se a existência de heterocedasticidade condicional na série a um nível de 10% de significância, sugerindo que se utilize, em pesquisas posteriores, modelos da família ARCH para a modelagem dos retornos do Ibovespa, com o intuito de capturar o comportamento da variância desigual da série. Pois, como se sabe, este mercado é fortemente e constantemente influenciado por notícias, boas ou ruins, que acabam se refletindo nos preços das ações, gerando momentos de incertezas na bolsa, isto é, em outras palavras, estes choques ou abalos, provocados pelas notícias, fazem com que a volatilidade dos preços das ações aumente, ampliando os riscos assumidos pelos investidores, tornando-se extremamente importante ter um método que auxilie os investidores na análise do comportamento deste mercado.
5 Referências bibliográficas
ARAUJO, SAULO. et al. "Precificação de ações: aplicação do modelo ARIMA para as empresas mais negociadas na BM&FBOVESPA". Congresso Fluminense de Iniciação Científica e Tecnológica, Rio de Janeiro, 3 a 6 de junho de 2013.
Banco Central do Brasil, 2014. Disponível em: <http://www.bcb.gov.br/>. Acesso em: abr. 2014.
BM&FBOVESPA, 2014. Disponível em: < http://www.bmfbovespa.com.br/>. Acesso em: abr. 2014.
BUENO, RODRIGO. Econometria de séries temporais. 1ª Ed. São Paulo: Cengage Learning, 2011.
GUJARATI, DAMODAR N. Econometria Básica. 4ª Ed. Rio de Janeiro: Elsevier, 2006.
Instituto Brasileiro de Geografia e Estatística (IBGE), 2014. Disponível em: < http://www.ibge.gov.br/>. Acesso em: abr. 2014.
Instituto de Pesquisa Econômica Aplicada (IPEA), 2014. Disponível em: < http://www.ipeadata.gov.br/>. Acesso em: abr. 2014.
KEYNES, JHON MAYNARD. (1936). Teoria Geral do Emprego do Juro e da Moeda. 1ª Ed. São Paulo: Abril Cultural, 1983.
LEROY, FELIPE. "Projeção do preço futuro de uma ação da Usiminas: uma abordagem Econométrica". Revista da Faculdade de Ciências Administrativas de Curvelo, Curvelo, MG, v. 5, n. 4, Outubro. 2006.
MORETTIN, PEDRO A. Econometria financeira: um curso de séries temporais financeiras. 1ª Ed. São Paulo: Blucher, 2008.
PIAZZA, M. C. Bem vindo a Bolsa de Valores. 8ª Ed. São Paulo: Novo Conceito Editora, 2009.
SANTOS, ISRAEL. "APLICAÇÃO DE MODELOS ARIMA EM SÉRIES DE PREÇOS DE SOJA NO NORTE DO PARANÁ". Tekhne e Logos, Botucatu, SP, v.3, n.3, Novembro. 2012.
1. Universidade Federal de Santa Maria (UFSM), Santa Maria, RS, Brasil. Raphael.Amaro@ufsm.br
2. Universidade Federal de Santa Maria (UFSM), Santa Maria, RS, Brasil. amsouza@mail.ufsm.br
3. Dados da variação do PIB brasileiro fornecidos pelo Instituto Brasileiro de Geografia e Estatística (IBGE).
4. Dados do saldo da caderneta de poupança fornecidos pelo Banco Central do Brasil.
5. O índice Bovespa representa o desempenho médio das cotações das 100 ações com maior volume negociado nos últimos meses dentro da BM&FBOVESPA.
6. Bolsa de Valores, Mercadorias e Futuros de São Paulo.
7. Disponível em <http://www.bmfbovespa.com.br/>.
8. A formalização dos testes de raiz unitária pode ser encontrada em BUENO, RODRIGO. Econometria de séries temporais. 1ª Ed. São Paulo: Cengage Learning, 2011.
9. Cabe aqui ressaltar que um processo puramente aleatório, dito ruído branco, possui média zero, a variância σ² é constante e ele é serial não correlacionado.
10. A formalização do teste ARCH-LM pode ser encontrada em BUENO, RODRIGO. Econometria de séries temporais. 1ª Ed. São Paulo: Cengage Learning, 2011.