Espacios. Vol. 35 (Nº 11) Año 2014. Pág. 21

Projeto de tolerâncias: Levantamento cronológico e perspectivas de inovação

Design tolerances: Chronological Survey and prospects for innovation

Roderlei CAMARGO 1, Carlos Roberto Camello LIMA 2

Recibido: 27/07/14 • Aprobado: 09/08/14

Contenido

1 Introdução

2. Procedimentos Metodológicos

3. Levantamento Cronológico da Evolução Conceitual

4. Teoria Matemática Aplicada

5. Conclusões

6. Referências Bibliográficas

1. Introdução

O mercado moderno demanda produtos cada vez mais sofisticados e especializados, onde são analisados a ergonomia, a funcionalidade, a eficiência, a durabilidade, o retorno do investimento e a produtividade, sob o ponto de vista dos stakeholders. Nguyen et al. (2010) relatam que, devido ao rápido desenvolvimento da tecnologia e a estreita competição entre as empresas, - dentro de um contexto global e da economia concorrente - os desejos dos clientes, como qualidade, confiabilidade, sustentabilidade e custo dos produtos, são cada vez mais exigidos. Então,  satisfazer estes requisitos é uma chave importante a ser considerada pelo projetista de produto.

Também afirma Weckenmann (2008) que, ao integrar desenho, engenharia e manufatura sob um mesmo teto, consegue-se produzir de acordo com as necessidades dos clientes e sob conceitos mais exigentes de produção, graças às recentes pesquisas em metrologia e sistemas de tolerâncias, principalmente, que é o foco da tríade formada pelo projeto, fabricação e controle de qualidade. O sucesso e a permanência de uma empresa neste mercado competitivo está diretamente ligada a sua capacidade de introduzir novos produtos em menores tempos e custos, aumentando a qualidade e o valor tecnológico agregado aos mesmos, na mesma proporção em que a confiabilidade do produto é convalidada pelos consumidores no nicho de mercado ao qual se destinam. Usando estas metodologias no desenvolvimento de um produto, estimar a tolerância por meio da análise, síntese e avaliação estatística, torna-se um elemento fundamental para a otimização do processo de montagem, diminuição do custo e redução do ciclo de vida de um produto (CROSTACK et al., 2010).

De acordo com Chase (2007), a análise de tolerância é uma função do processo produtivo, sendo realizada depois das peças serem manufaturadas. Os passos principais para uma boa análise são: 1) obtenção dos dados dos componentes  referentes a variação individual; 2) criação de um modelo de montagem para identificar qual cota mais contribui para com a dimensão final de montagem; 3) aplicação da variação medida do componente para o modelo, prevendo a variação dimensional de montagem. Sendo assim, a análise de tolerância não só estima os efeitos da variação da manufatura sobre as dimensões da montagem do produto, como provê uma ligação importante entre o projeto de engenharia e a manufatura, sendo uma ferramenta que quantifica o efeito da variação da montagem dos componentes sobre as especificações de desempenho. A análise de tolerância acopla a capabilidade da manufatura e os requisitos de desempenho dentro de um modelo de engenharia, provendo um ambiente comum de integração onde o projeto e a manufatura podem interagir e avaliar quantitativamente os efeitos dos seus respectivos requisitos.

Ainda conforme Chase (2007), a síntese de tolerância (função de projeto) é um procedimento inverso da análise, ou seja, é constituída no início do ciclo de desenvolvimento do produto, antes que qualquer peça seja produzida ou mesmo antes da ordem de construção do ferramental. O processo de síntese de tolerância envolve 3 estágios: 1) decisão do limite de tolerância a ser colocado nas folgas críticas e ajustes para uma montagem baseada nos requisitos de desempenho; 2) criação de um modelo de montagem para identificar que cotas contribuem com as dimensões da montagem final; 3) decisão do quanto da tolerância de montagem será majorada para cada componente montado. Em suma, consiste em se determinar as tolerâncias individuais das peças, sendo que a sua soma vai ao encontro da especificação da tolerância de montagem (requisitos de projeto), considerando que a magnitude da tolerância dos componentes para cumprir este requisito é desconhecida.

A avaliação estatística é uma iteração via checagem das características relevantes, onde procede-se a síntese e otimização da tolerância, cujo principio, por ser um método promissor de alocação de tolerância, utiliza as técnicas de otimização para atribuir tolerâncias aos componentes, tais que os custos de produção de uma montagem sejam minimizados (CHASE, 2007). Isto é realizado pela correta definição de uma curva de custo versus tolerância de cada componente da montagem. Neste método, a otimização do algoritmo estocástico varia a tolerância de cada componente e pesquisa sistematicamente pela combinação de tolerância que melhor minimize o custo.

Fazendo uma comparação, a análise de tolerância estima a porcentagem de rejeição oriunda da variação da especificação dos componentes, enquanto a atribuição de tolerância determina um conjunto de tolerâncias de componentes contendo as especificações admissíveis do limite de rejeição. Geralmente, o desenvolvimento de um produto é um processo evolutivo. Modificações feitas ao projeto original são introduzidas ao longo do período de desenvolvimento do produto, de tal forma que as informações obtidas na revisão anterior do projeto possam não ser mais relevantes ao produto, considerando o avanço tecnológico dos sistemas (DROGUETT e MOSLEH, 2006). Daí a importância destas modificações serem efetuadas na fase inicial de desenvolvimento do produto. Devido à crescente complexidade dos produtos, a confiabilidade do sistema de tolerância transforma-se num parâmetro de projeto, difícil de definir e conseguir. Entretanto, a experiência prática tem mostrado que a correta variação geométrica da peça, por meio da cadeia de dimensionamento, é reconhecida como um requisito necessário para se desenvolver um produto e também pela aplicação de técnicas de tolerâncias, durante o processo de desenvolvimento do ciclo de vida do produto. A tolerância pode, então, ser quantificada durante a especificação dos requisitos de projeto, podendo ser prevista por hipóteses estocásticas e simulações computacionais orientadas a objetos 3D, onde facilmente é possível analisar, sintetizar, visualizar e entender a tolerância geométrica e a variação dimensional que impactam no projeto do produto. Também a tolerância pode ser controlada na produção, garantindo uma adequada sustentabilidade do produto, durante sua vida útil no campo.

Neste contexto, e considerando o projeto de tolerâncias cada vez mais presente na fase de criação do produto dentro das indústrias, este trabalho discute algumas metodologias relacionadas ao projeto de tolerâncias, apresentando uma aplicação do método discutido.

2. Procedimentos Metodológicos

Este trabalho pode ser dividido, basicamente, em 3 etapas: i) definição do problema; ii) revisão bibliográfica com resumo e discussão das técnicas propostas na literatura e iii) estudo de aplicação do método proposto. Sobre a definição do problema, o início deste trabalho surgiu da necessidade de maior conhecimento acerca dos requisitos relacionados ao projeto de tolerâncias, mais especificamente nas questões envolvendo a engenharia de projeto e a manufatura do produto. Se de um lado a engenharia procura apertar ao máximo a tolerância, provocando um aumento no custo do produto e, do outro lado, a manufatura procura afrouxar a tolerância como forma de adequação do seu processo de fabricação, então é necessária uma estratégia que leve em conta os requisitos competitivos que se deseja priorizar, apertando o conjunto de atividades inerentes ao projeto de engenharia ou afrouxando as atividades inerentes à manufatura. Quanto à revisão bibliográfica, foi focada no estudo realizado pela leitura e síntese de livros de autores renomados na área, artigos e periódicos, que forneceram e esclareceram os conceitos de aplicação das diversas técnicas disponíiveis para otimização do projeto e do processo de fabricação do produto. No estudo de aplicação das técnicas estudadas eselecionadas, escolheu-se um produto da linha de bens de consumo (serra mármore), evidenciando o conjunto estator e induzido, sendo realizado um estudo de otimização dimensional, via análise de tolerância, como forma de controlar os parâmetros de projeto robusto.

3. Levantamento Cronológico da Evolução Conceitual

Esta parte do trabalho tem a finalidade de apresentar as principais metodologias e filosofias do sistema de tolerâncias, na visão de projeto e processo, que são aplicáveis durante a fase de projeto, relacionadas ao projeto de tolerâncias. Por se tratar de um tema de grande abrangência na grande área da engenharia de desenvolvimento, especificamente para a fase do projeto do produto, descrevem-se alguns aspectos abordados nas dimensões do conhecimento, desde a criação das primeiras pesquisas, envolvendo os trabalhos acadêmicos, até o atingimento do apogeu tecnológico, onde se sugerem algumas tendências inovadoras referentes ao sistema de tolerância como parte do gerenciamento do ciclo de vida do produto.

A partir do levantamento histórico, apresentam-se as principais metodologias aplicadas em sistemas de tolerâncias, procurando traçar um panorama atual e identificando futuras possibilidades de utilização do projeto de tolerâncias. Como fontes de pesquisa, foram utilizados livros especializados no assunto, artigos disponíveis nas bases de consulta, páginas eletrônicas e outras entidades acadêmicas de primeira linha, que fornecem subsídios para pesquisa. Especificamente, foram realizados estudos nas bases Sciencedirect, Springerlink e periódicos do Engineering Village Compendex.

Em 1976, a simulação pelo método de Monte Carlo foi efetivamente implementada para a resolução de um problema de análise de tolerância. Neste artigo, os autores Corlew e Oakland (1976) descrevem, passo a passo, todo o processo estocástico relacionado ao estudo de um modelo virtual, representado por um processo matemático que executa uma randomização baseada nas suas distribuições probabilísticas. A evolução das pesquisas e publicações de artigos sobre análise de tolerância dá conta que, a partir de 1987, Greenwood e Chase (1987) desenvolvem um grande estudo, o qual foi chamado de "novo método de análise de tolerância", destinado a um público alvo composto a priori por profissionais engenheiros e projetistas. Este método abrange tanto a análise quanto a síntese de tolerância, capacitando o engenheiro projetista para incorporar os efeitos da variação da manufatura, já nas fases iniciais do projeto do produto, possibilitando prever o seu comportamento probabilístico por meio dos métodos não lineares, Simulação de Monte Carlo e Método dos Momentos Combinados, e obter uma otimização das tolerâncias geométricas do produto final com redução significativa no custo do produto, fazendo com que o tempo de desenvolvimento seja também bem menor quando comparado com outros métodos convencionais de projeto. Em 1.988, a pesquisa assume uma nova abordagem dirigida aos profissionais tecnocratas, porém, com a inclusão da estatística dimensional, que vem a ser um processo estocástico relacionado aos limites das tolerâncias. Greenwood e Chase (1988) afirmam ser uma forma de problematizar as análises não lineares, incluindo na análise da tolerância os casos de "Worst Case" (pior caso), considerando os limites estatísticos de variação permitidos e problemas de análises não lineares.

Chase et al. (1990) alocam os custos das tolerâncias nas montagens mecânicas por meio da seleção automática de processos, o que não foi muito bem aceito devido a não comprovação prática dos argumentos teorizados. Em 1990, a pesquisa foi acrescida de uma nova linha de pensamento, a somatória da raiz quadrada (RSS - Root Sum Square). Chase e Greenwood (1990) discutem este método de modo convergente para a análise não linear. A partir de 1991, Chase e Parkinson (1991) executam uma pesquisa voltada à aplicação da análise de tolerância para o projeto de montagens mecânicas, dentro da área de engenharia de produto. Logo a seguir, Carr (1993) resolve agrupar os requisitos das tolerâncias de engenharia com as restrições da manufatura, usando um modelo comum de engenharia capaz de identificar as variações da montagem do conjunto. Desenvolveu-se um sistema dedicado para definir as especificações de montagem (requisitos de engenharia) e para prever, de forma analítica, as variações desta montagem, permitindo um controle da qualidade do produto e seu desempenho. Foi criada uma malha de vetores para modelar o conjunto mecânico. Esta malha, agrupa as dimensões formando cadeias de elementos, onde as malhas fechadas definem as restrições cinemáticas da montagem, e as malhas abertas definem as restrições de engenharia.

Devido ao grande gap entre os dois mais populares métodos de análise de tolerância: método de linearização ou soma da raiz quadrada (RSS) e método de Monte Carlo, Glancy (1994) definiu um novo método para análise de tolerância de peça, o qual denominou de método de segunda ordem para análise de tolerância (SOTA_part – Second-order Tolerance Analysis), que leva em conta algumas características de estatística, como forma de convergir para uma metodologia mais assertiva, pois no método de linearização é previsto: análise rápida, as restrições são em malha fechada, alocação de tolerância e iteração de projeto, enquanto no método de simulação de Monte Carlo uma intensa computação é requerida devido à grande precisão interna do modelo CAD e dos efeitos não lineares da geometria da montagem. Com isto, este novo método SOTA_part tenta combinar as vantagens do método linear com os ganhos da simulação de Monte Carlo, contemplando os seguintes benefícios: velocidade, alocação de tolerância e restrição em malha fechada.

Em 1995, a pesquisa assume uma nova linha de pensamento conduzida por Magleby et al. (1995), desta vez voltada a pequenos ajustes cinemáticos de montagens mecânicas, sendo então analisadas no ambiente 2D e fazendo uso da simulação pelo método de Monte Carlo modificado. Também têm início os estudos por Gao et al. (1995) referentes a uma nova técnica de análise de tolerância, o método de linearização direta (DLM – Direct Linearization Method), para ser usado em análise de tolerância 2-D e 3-D de conjuntos mecânicos. O método DLM usa uma restrição de montagem e uma matriz algébrica para estimar a variação da montagem ou a variação cinemática, prevendo assim as não conformidades desta montagem. O resultado da comparação com o método de Monte Carlo reside no fato do método DLM ter maior acuracidade de cálculo se as tolerâncias forem relativamente pequenas, quando comparadas com as dimensões nominais dos componentes. Por outro lado, o tamanho das amostras denota ter uma grande influência sobre a exatidão na simulação considerando o método de Monte Carlo. Publicado por Liu e Hu (1995), foi usado um modelo de elemento finito simplificado para prever a variação da montagem de chapas dobradas flexíveis, sendo este trabalho focado no efeito da fixação destas peças e na ordem da montagem, não sendo considerado o efeito da variação da superfície na montagem flexível.

Preconizado por Sorenson et al. (1996), houve a inclusão da variação geométrica das características do modelo CAD, fazendo aderência à análise de tolerância de montagens mecânicas. Também surge, em 1996, um novo método para a determinação da sensibilidade de montagens, o método da variação poligonal, que trata da análise de tolerância de sistemas flexíveis, trabalho este desenvolvido por Merkley et al. (1996) como alternativa ao método de Sorenson (variação geométrica das features). Huo e Chase (1996) melhoram o método da variação poligonal de Merkley e implementam o método da sensibilidade das tolerâncias em conjuntos montados.

Alternativamente e corroborando com a visão de modelo estatístico simplificado, Bisgaard (1997) propôs o uso do experimento fatorial, afirmando ser uma proposta alternativa ao método de tentativa e erro, visando a avaliar o limite do projeto de tolerância quando se tratar de montagens de produtos, onde deseja-se promover o acoplamento de componentes, sob diversos tipos e restrições de graus de liberdade (translação e rotação), referentes aos três planos cartesianos "X", "Y" e "Z" que, por sua vez, relacionam-se com os ângulos tensores: Roll, Pitch e Yaw.

Entre 1997-1998, os estudos envolvendo a cinemática das partes, conforme Gao et al. (1997, 1998), evoluíram para uma abordagem 2D e 3D referente à análise de tolerância, convergindo ao método da coordenada global, com o escopo de se determinar a sensibilidade em análise de tolerâncias de montagens, assim como a inserção de novas métricas ao método de Monte Carlo, orientadas ao ambiente do modelo matemático CAD, composto de pequenas montagens. De acordo com Chase (1999, 1999a), aprimoraram-se os estudos referentes aos custos de tolerâncias nas montagens mecânicas e publicou-se uma nova literatura de alocação de tolerância, contemplando o projeto para mínimo custo (Design for Minimum Cost), assim como a análise de tolerância multidimensional. Também surge o método de segunda ordem (SOTA_assembly), descrito por Glancy e Chase (1999), destinado à análise de tolerância de montagens e adaptado ao projeto robusto de montagens mecânicas.

Bihlmaier (1999) teoriza a análise de tolerâncias de montagens flexíveis usando um novo método para modelamento da montagem de componentes, representando a superfície variacional das peças via série de Fourier (análise espectral de freqüência), método este em que o modelo espectral de freqüência pode ser usado para representar qualquer contorno da peça, incluindo ambos os contornos: nominal e variável. A partir deste modelo espectral de freqüência, informações estatísticas podem ser obtidas e utilizadas como entrada no elemento finito que recobre a peça. Assim, este elemento pode ser usado para prever a probabilidade da série de forças, tensões e deformações das peças devido à montagem do conjunto. Este método proposto é batizado de FASTA, num acrônimo para Flexible Assembly Spectral Tolerance Analysis.

Parkinson e Chase (2000) iniciam os estudos para acoplar a análise de tolerância ao método de projeto robusto dentro da engenharia de projeto e utilizando sistemas CAD 3D em plena fase de projeto conceitual, relativo a montagens mecânicas.         Maghsoodloo e Li (2000) consideram a função perda linear quadrática para determinação da média do processo ótimo, de acordo com os argumentos de Taguchi (1986) para projeto robusto, ou seja, minimizando os valores  da função perda da qualidade, para valores de tolerâncias assimétricos, conforme a voz do produto.

Wittwer et al. (2001) estudam a previsão do posicionamento errôneo em ligações (links) cinemáticas, fazendo uma comparação entre os métodos determinísticos e probabilísticos. Também são relatados os efeitos das folgas em juntas planares de micro-mecanismos, graças ao modelamento matemático e às facilidades dos sistemas de informática científica CAD e CAE. Downey et al. (2002) aplicam o conceito de tolerância de juntas flexíveis ao projeto robusto postulado por Taguchi (1986) como forma de integrar os desenvolvimentos de montagens em projetos de engenharia. Para resolver o problema de montagens mecânicas no projeto robusto, Pearce et al. (2003) solucionam esta não conformidade adotando o projeto de forças de assentamento para montagens restritas em conjuntos cinemáticos.

Wittwer et al. (2004), baseando-se nos estudos de Magleby et al. (1995), implementam o método de linearização direta (DLM) aplicado para o posicionamento errôneo em ligações (links) cinemáticas, cujo nicho de aplicação dá-se em sistemas de mecanismos e construções mecânicas de máquinas.  Os modelos CAD são construídos por elementos comuns da engenharia: cadeia de vetores, juntas cinemáticas, datums de conjunto, tolerâncias dimensionais, tolerâncias geométricas do feature e limites de tolerância do conjunto. Este método é indicado para se integrar aos diversos sistemas CAD existentes, aproximando a matriz algébrica e o erro quadrático (RSS) ao vetor do modelo base, como forma de estimar a pilha de tolerância nos conjuntos montados. Três fontes de variações aparecem nestes modelos, quais sejam: dimensional, geométrica e cinemática. Variações dimensionais acarretam pequenas mudanças no tamanho devido ao processo de manufatura. Variações geométricas promovem mudanças na forma, na posição e na orientação das características geométricas. Variações cinemáticas descrevem a propagação da variação da montagem por meio de pequenos ajustes entre as peças dos acoplamentos. O método DLM, por não usar computação intensiva, é ideal para o projeto iterativo, onde os algoritmos de alocação das tolerâncias podem ser aplicados sem a repetição das análises.

Tonks e Chase (2004), com base na análise de tolerância estatística de montagem, introduzem o método de modelamento covariacional, dedicado ao conjunto de componentes.

Em 2005, uma nova linha de raciocínio surge para fortalecer a análise de tolerância estatística de montagem, quando Tonks e Chase (2005) introduzem o polinômio de superfície covariacional, relacionando a metodologia Seis Sigma, tanto para o projeto, quanto para a manufatura, considerando a análise de tolerância como elemento vital para as novas técnicas de engenharia off-line, dentro do ciclo de vida do produto. A engenharia off-line de projeto e fabricação classe mundial compreende algumas ferramentas tecnológicas destinadas à prevenção de eventos não conformes, durante a fase de desenvolvimento do conceito, dentro do processo de desenvolvimento do produto.

Define-se engenharia off-line como sendo as ferramentas tecnológicas que possuem, como características principais, uma orientação baseada em critérios sistêmicos preventivos. Estes critérios preventivos identificam a causa raiz e, posteriormente, indicam a melhor solução adequada à resolução do problema em questão, tendo como prerrogativa heurística os critérios de falhas, seus efeitos e a prioridade de risco baseados na detecção, severidade e ocorrência do evento não conforme. Constituem exemplos de engenharia off-line: FMEA (Análise do Modo de Falha e seus Efeitos) de sistema, de projeto, de processo e ecológico; FMECA (Análise Critica do Modo de Falha e seus Efeitos); TRD (Projeto Robusto de Taguchi); DRBFM (Revisão de Projeto Baseado em Critérios de Falha); FTA (Análise da Causa Raiz); EQFD (Desdobramento Avançado da Função Qualidade); AGF (Análise dos Geradores de Falha); TRIZ (Teoria da Solução Inventiva de Problemas); WOIS (Estratégia de Inovação de Orientação Contrária) e QFD (Desdobramento da Função Qualidade).

Tonks et al. (2006) melhoram os entendimentos relativos ao modelamento covariacional e adicionam à análise de tolerância elementos estatísticos covariacionais, como forma de prever a deformação de montagens concorrentes. Em 2007, os estudos e pesquisas, conforme Chase (2007), foram dedicados a um sistema abrangente de análise de tolerância, com aplicação em montagens de conjuntos mecânicos, dentro de um ambiente rígido de processo de montagem e dependente das variações do modelo virtual.

Jérome e Denis (2008) apresentam uma estrutura de dados colaborativa centrada no modelo do produto para suportar a tolerância geométrica, em qualquer fase do desenvolvimento do projeto. Significa que o modelo matemático CAD do produto permite que projetistas descrevam as especificações geométricas em qualquer fase do ciclo de projeto, incluindo tolerância de forma, de posição, de orientação e localização. A proposta destes autores é criar um ambiente de engenharia colaborativa, onde diversos especialistas inserem os dados diretamente no modelo matemático (CAD, manufatura, tolerância geométrica, modelo de elementos finitos), de forma concorrente.

Chase (2008) dedica-se à pesquisa de montagens de peças flexíveis - usadas em produtos domésticos, defletor de ar, chassi elétrico e peças plásticas – por meio de um novo sistema de análise de tolerância de montagem: combinação da análise estatística de tolerância, elementos finitos e da análise de resposta espectral. Assim, a intenção é prever a variação geométrica do perfil, tensões residuais e o efeito mola devido à variação dimensional e variação de forma em processos de montagens flexíveis.

Dantan e Qureshi (2009) publicam um trabalho evidenciando uma nova técnica matemática baseada em quantificadores universais "", os quais fornecem uma expressão unívoca da condição, correspondente a uma exigência geométrica do produto. A formulação matemática da análise de tolerância, simula as influências dos desvios geométricos e dos tipos de elementos de contatos, no comportamento do mecanismo, integrando os quantificadores Universal e Existencial como requisitos funcionais do projeto. Adragna et al. (2010) apresentam uma abordagem para toleranciamento estatístico 3D utilizando um novo critério de aceitação. A abordagem baseia-se no critério de aceitação 1D inercial que se estende a 3D e aceitação de forma. A caracterização modal é usada para descrever o desvio de forma de uma geometria como a combinação dos desvios elementares (localização, orientação e forma).

Yu et al. (2011) propuseram um método de análise não linear de tolerância que utiliza ferramenta Matlab para construir a formulação matemática e calcular o resultado de análise de tolerância não linear com base no princípio de análise de tolerância worst case, com todos os processos tratados e testados por computador. Os engenheiros apenas informam alguns parâmetros básicos através da interface normalizada, e, em seguida, o resultado pode ser obtido sem intervenção artificial. A Tabela 1 ilustra um registro ordenado de contribuições metodológicas e seus autores correlatos, destacando o ano de sua criação.

De posse dos conceitos apresentados e após uma análise abrangente sobre as características, fatores positivos e dificuldades inerentes a cada proposição existente, propõe-se um método de análise que facilite a determinação e a otimização da tolerância geométrica, migrando-se do atual sistema de representação intuitiva do projetista para um sistema digital.

A teoria matemática a ser aplicada para a tolerância geométrica será o princípio de GD&T (Geometric Dimensioning and Tolerancing) - Tolerância de perfil, forma, batimento, localização e orientação - via método estatístico de Monte Carlo. Neste caso, está previsto o uso do software VisVSA, da empresa Siemens, cujo pacote gráfico executa uma série de simulações virtuais, com base nas características geométricas (features) e nos meta dados do modelo matemático CAD.

4. Teoria Matemática Aplicada

A simulação de Monte de Carlo é uma ferramenta computacional que torna possível uma aproximação matemática entre a manufatura e o processo de montagem, permitindo fazer decisões de projeto baseado no desempenho destes processos e, ao mesmo tempo, provendo a oportunidade de analisar o projeto antes da produção.

Dantan e Qureshi (2009) comentam que este método de simulação usa perturbações randômicas (aleatórias) das dimensões das peças, dentro das tolerâncias, para simular a população de uma montagem completa. Desta forma, as tolerâncias de montagens podem ser verificadas via programa de simulação de produção. No método de Monte Carlo, conforme Mark e Stember (1965)  um grande número de réplicas é simulado via modelo matemático, formando as variáveis e os seus respectivos parâmetros. Os valores destas variáveis e parâmetros são randomicamente selecionados, com base nas suas distribuições probabilísticas.

O custo do retrabalho e rejeição da peça pode ser eliminado ou reduzido para um nível aceitável, antes que o projeto alcance a manufatura. Precedendo a análise da função de montagem, o método de Monte Carlo utiliza quatro momentos - medidas descritivas de caráter mais geral - em torno da média da distribuição estatística, para quantificar a variabilidade dentro do projeto do produto e do processo de manufatura.

Tabela 1. Taxonomia metodológica da época e as contribuições tecnológicas

A Figura 1 ilustra o diagrama de blocos do método de Monte Carlo, evidenciando o modo e o grau dos quatro momentos estatísticos: i) Média aritmética (momento de 1ª.ordem); ii) Desvio padrão (momento de 2ª.ordem); iii) Assimetria (momento de 3ª.ordem); iv) Curtose (momento de 4ª.ordem). O desempenho total do sistema pode ser comparado a um conjunto de especificações, sendo que o elevado número de valores de desempenho deste sistema é usado para desenvolver uma freqüência de distribuição do sistema. A distribuição resultante, gerada pelo método de Monte Carlo, é usada para calcular a porcentagem de rejeição da montagem dentro do lote, assim como o índice de capacidade de processo, a variância, a média e o desvio padrão, conforme ilustrado na Figura 2.  

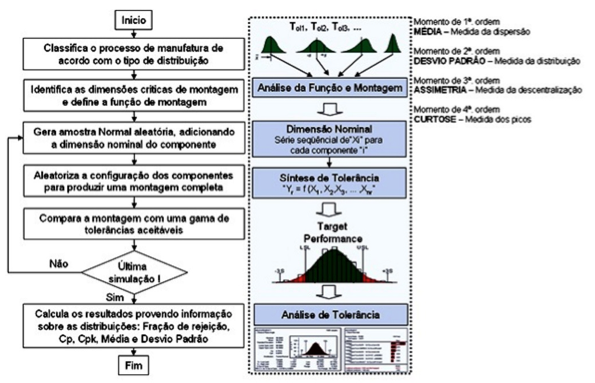
Figura 1. Fluxograma do método de Monte Carlo (DANTAN e qureshi, 2009)

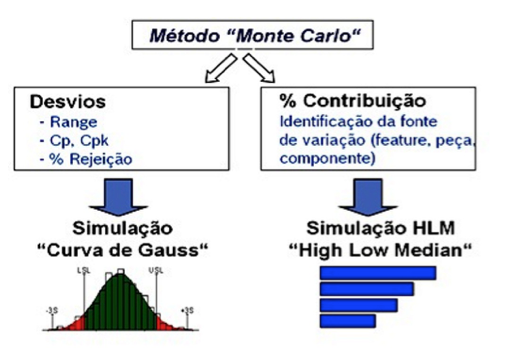
Figura 2. Simulação de Monte Carlo: Curva de Gauss e "HLM"

Para auxiliar o entendimento e exemplificar a aplicação das técnicas mencionadas (Monte Carlo), apresenta-se um produto da linha de bens de consumo, destacando-se o conjunto induzido, sendo realizado um estudo de otimização dimensional, via análise de tolerância, utilizando-se os recursos computacionais do software Vis_VSA (Siemens). No workflow representado pela Figura 3, a análise de tolerância é o portal de entrada das operações de montagens, através do modelo CAD, do processo, das tolerâncias e da montagem.

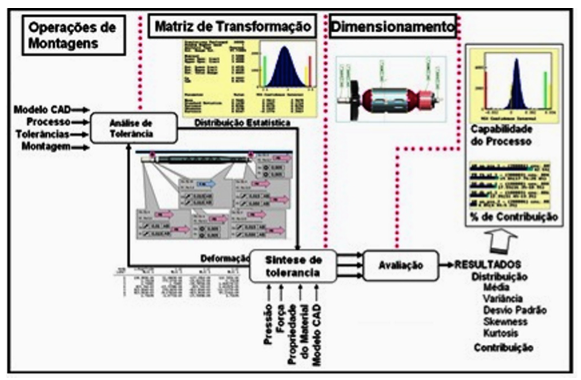
Figura 3. Workflow da metodologia de Análise de Tolerância

O próximo passo é a matriz de transformação que gera a distribuição estatística das dimensões mais representativas. Estas dimensões são os dados de entrada para a síntese de tolerância, que também leva em consideração: pressão, força, propriedade do material e o modelo CAD, tendo como resultado a otimização dimensional. Segue com a avaliação evidenciando o dimensionamento do modelo matemático CAD e tendo como saída os resultados inerentes à análise realizada, ou seja: distribuição (capacidade do processo "Cp e Cpk", média, variância, desvio padrão, curtose e centralização da Gaussiana) e percentual de contribuição de cada dimensão.

A Figura 4 denota uma análise de tolerância realizada no conjunto estator/induzido de uma serra mármore, onde ficam evidenciadas duas análises realizadas: i) no induzido do motor, onde nota-se a curva de Gauss seguida da porcentagem de contribuição de cada cota dimensional deste conjunto, desta forma auxiliando o engenheiro projetista na tomada de decisão do melhor valor a atribuir no sistema de cotagem, visando a uma adequação ao sistema de qualidade; ii) no eixo do induzido, como forma de garantir uma estratégia de usinagem, fazendo aderência aos requisitos de projeto. 

Neste estudo, realizou-se um total de 5.000 simulações no produto induzido via método de Monte Carlo e observou-se que os valores de Cp e Cpk ficaram em torno de 1,35, o que excede a qualificação, considerando o sistema de qualidade 3 Sigma. Também se realizou um total de 5.000 simulações para o eixo do induzido e os valores de Cp e Cpk ficaram em torno de 2,1, o que também excede a qualificação para a qualidade 3 Sigma.

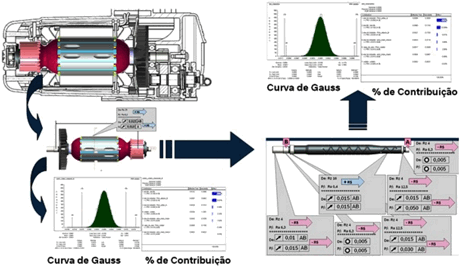
Figura 4. Análise de tolerância do conjunto induzido e eixo

De acordo com Creveling (1997), o  termo Cp é o índice de capacidade que é definido como a amplitude da tolerância dividida pela capacidade do processo, sem preocupar-se com a centralização do processo. É expresso pela fórmula:

As características "LSE e LIE" delimitam os limites superior e inferior de especificação, conforme exigências do projeto. Em geral, dados o limite superior de especificação (LSE) e o limite inferior de especificação (LIE), um processo estará centralizado se a média () da amostra for igual à média aritmética entre os limites de especificação:

O termo Cpk é o índice de capacidade que leva em conta a centralização do processo, definido como o mínimo entre Cps (índice de capacidade superior) e Cpi (índice de capacidade inferior). Relaciona a distância entre a média do processo e o mais próximo limite de especificação, com a metade da capacidade do processo.           

Capacidade potencial inferior (Cpi):

Capacidade potencial superior (Cps):

Desta forma, o Cpk é obtido tomando o mínimo entre esses dois índices:

O Cpk indica, também, a proporção entre a posição da média e os limites de especificação em relação ao desvio padrão. A comparação entre os dois índices Cp e Cpk é uma importante informação para que se possam manter os processos centralizados em torno do valor médio.  Portanto, é verdadeira a afirmação:

5. Conclusões

Neste trabalho, apresentou-se uma topologia histórica das diversas metodologias tecnológicas referentes ao projeto de tolerância, com suas respectivas justificativas filosóficas, inerentes ao estágio da evolução da tecnologia. Estas metodologias propostas possibilitam fazer uso de informações avançadas com o escopo de prever o comportamento geométrico e variacional referente ao sistema de tolerância, já na fase inicial do projeto, especificamente na fase inicial de desenvolvimento do produto.

Quanto à contribuição para o conhecimento, o projeto de tolerância tem uma função de extrema importância no processo de desenvolvimento de produto, capaz de atender aos requisitos do projeto robusto e fazendo aderência ao gerenciamento do ciclo de vida do produto e, também, mantendo a rastreabilidade das tolerâncias durante o processo de projeto. Assim, a solução para integrar a síntese de tolerância no processo de projeto, otimizando o processo de desenvolvimento do produto, dar-se-á pelo conjunto final de cotas e tolerâncias, obtendo o compromisso ideal entre o que é tecnicamente possível e o que é desejável pelos clientes: custo (menor), prazo (menor) e qualidade (maior).

Como perspectiva de evolução no tema aqui discutido, no campo do projeto de tolerâncias, aponta-se para a direção da integração total e colaborativa do sistema de análise de tolerâncias com as novas técnicas de engenharia off-line, a qual está inserida no gerenciamento do ciclo de vida do produto, sendo que quanto mais cedo o sistema de tolerância for integrado à metodologia de projeto, obter-se-á uma redução de custo no desenvolvimento do produto na mesma proporção em o produto chegará mais cedo ao mercado, contribuindo para a redução do tempo de lançamento do produto no mercado consumidor (time-to-market).

6. Referências Bibliográficas

ADRAGNA, P.-A., SAMPER, S., PILLET, M.A. A proposition of 3D inertial tolerancing to consider the statistical combination of the location and orientation deviations. Int. J. Prod.Dev. 10 (2010) 26-45.

BIHLMAIER, B. Tolerance Analysis of Flexible Assemblies Using Finite Element and Spectral Analysis, M.S. Thesis, BYU, Provo, UT, 1999.

BISGAARD, S. Designing experiments for tolerancing assembled products, Technometrics 39 (1997) 142-152.

CARR, C.D. A comprehensive method for specifying tolerance requirements for assemblies, M.S. Thesis, Mechanical Engineering Department, Brigham Young University, Provo, UT, 1993

CHASE, K.W. Chap. 13 – "Multi-Dimensional Tolerance Analysis", pp. 1-27, In: Dimensioning and Tolerancing Handbook, Ed. Drake, P., McGraw-Hill, 1999.

CHASE, K.W. Chap. 14 – "Minimum-Cost Tolerance Allocation", pp. 1-23. In: Dimensioning and Tolerancing Handbook, Ed. Drake, P., McGraw-Hill, 1999.

CHASE, K.W. Pagina pessoal do pesquisador, http://www.byu.edu, acesso em 19/12/2008, Brigham Young University, Provo, UT, 2008.

CHASE, K.W., "A Comprehensive System for Tolerance Analysis of Assemblies," and "Modeling Compliance & Variation in Fixtured Assembly Processes," General Motors Technical Center Seminar, Warren, MI, 2007.

CHASE, K.W., GREENWOOD, W.H., LOOSLI, B.G., HAUGLUND, L.F. "Least Cost Tolerance Allocation for Mechanical Assemblies with Automated Process Selection," Manuf. Rev. 3 (1990) 1-22.

CORLEW, G., OAKLAND, F. Monte Carlo Simulation for Setting Dimensional Tolerances, Mach. Des. (1976) 91-95.

CREVELING, C.M. Tolerance Design: A Handbook for Developing Optimal Specifications, Addison Wesley Longman Inc., ISBN 0-201-63473-2, 1997.

CROSTACK, H.A., REFFLINGHAUS, R., LIANGSIRI, J.DEFINING Tolerances in Assembly Process with the Aid of Simulation, in: IPAS 2010, IFIP AICT 315, Ed. Ratchev, S., IFIP, 2010, pp. 33-40

DANTAN, J.-Y., QURESHI, A,-J. Worst-case and statistical tolerance analysis based on quantified constraint satisfaction problems and Monte Carlo simulation, Comput Aided Des. 41 (2009) 1-12.

DOWNEY, K., PARKINSON, A., CHASE, K.W. Smart Assemblies for Robust Design: A Progress Report," in: Proceedings of the 2002 ASME Design Automation Conference, 2002.

DROGUETT, E.L., MOSLEH, A. Análise Bayesiana da Confiabilidade de Produtos em Desenvolvimento, Revista Gestão e Produção, 13 (2006) 57-69.

GAO, J., CHASE, K.W., MAGLEBY, S.P. Comparison of Assembly Tolerance Analysis by the Direct Linearization and Modified Monte Carlo Simulation Methods, in: Proceedings of the ASME Design Engineering Technical Conferences, Boston, MA, (1995), pp. 353-360.

GAO, J., CHASE, K.W., MAGLEBY, S.P. General 3-D Tolerance Analysis of Mechanical Assemblies with Small Kinematic Adjustments, IIE Trans. 30 (1998) 367-377.

GAO, J., CHASE, K.W., MAGLEBY, S.P. Tolerance Analysis of 2-D and 3-D Mechanical Assemblies with Small Kinematic Adjustments", in: Advanced Tolerancing Techniques, Edited by H-C. Zhang, John Wiley (1997) pp. 103-137.

GLANCY, C.G. A second-order for assembly tolerance analysis, M.S. Thesis, Mechanical Engineering Department, Brigham Young University, Provo, UT, 1994

GLANCY, C.G., CHASE, K.W. A Second-Order Method for Assembly Tolerance Analysis, in: Proceedings of the ASME Design Engineering Technical Conferences, Las Vegas, NV, 1999.

GREENWOOD, W.H., CHASE, K.W. A New Tolerance Analysis Method for Designers and Manufacturers, J. Eng. Ind. 109 (1987) 112-116.

GREENWOOD, W.H., CHASE, K.W. Worst Case Tolerance Analysis with Non-linear Problems, J. Eng. Ind. 110 (1988) 232-235.

HUO, H., CHASE, K.W. Variation Polygon - a New Method for Determining Tolerance Sensitivity in Assemblies," in: Proceedings CSME Forum, Ontario, 1996.

JÉROME, D., DENIS, T. A tolerancing framework to support geometric specifications traceability, Int. J. Adv. Manuf. Tech. 36 (2008) 894-907.

K.W. Chase, A.R. Parkinson, A Survey of Research in the Application of Tolerance Analysis to the Design of Mechanical Assemblies", in: Res. Eng. Des. 3 (1991) 23-37.

K.W. Chase, W.H. Greenwood, Root Sum Squares Tolerance Analysis with Nonlinear Problems, J. Eng. Ind., 112 (1990) 382-384.

LIU, S.C., HU, S.J. An Offset Finite Element Model and its Application in Predicting Sheet Metal Assembly Variation, Int. J. Mach. Tool Manu., 35 (1995) 1545-1557.

MAGHSOODLOO, S. LI, M.H. Optimal asymmetric tolerance design, IIE Trans. 32 (2000) 1127-1137.

MAGLEBY, S.P., CHASE, K.W., GAO, J. General 2-D Tolerance Analysis of Mechanical Assemblies with Small Kinematic Adjustments", J. Des. Manuf. 5 (1995).

MARK, D.G.,  STEMBER Jr., L. H. Variability Analysis, Electro-Technol. 76 (1965) 37-48.

MERKLEY, K.G., CHASE, K.W., PERRY, E. An Introduction to Tolerance Analysis of Flexible Systems, MSC World Users Conference, CA, 1996.

NGUYEN, D.S., VIGNAT, F., BRISSAUD, D. Product performance simulation with geometric deviations throughout its life cycle, In: DET 2009 Proceedings, Huang, G. et al. (Eds.), AISC 66, Springer-Verlag, Heidelberg, 2010, pp. 79-95.

PARKINSON, A.R., CHASE, K.W. An Introduction to Adaptive Robust Design for Mechanical Assemblies, in: Proceedings of the ASME Design Eng. Tech. Conferences, Baltimore, MD, 2000.

PEARCE, E., PARKINSON, A., CHASE, K.W. On the Design of Nesting Forces for Exactly Constrained, Robust Mechanical Assemblies", ASME Design Automation Conference, Chicago, IL, 2003.

SORENSON, C.D., CHASE, K.W., GAO, J., MAGLEBY, S.P. Including Geometric Feature Variations in Tolerance Analysis of Mechanical Assemblies, IIE Trans. 28 (1996) 795-807.

TAGUCHI, G. Introduction to Quality Engineering: Designing Quality intoProducts and Processes, Asian Productivity Organization, Tokyo, 1986.

TONKS, M. R., CHASE, K.W. Covariance Modeling Method for Use in Compliant Assembly Tolerance Analysis", ASME Design Automation Conference, Salt Lake City, UT, 2004.

TONKS, M. R., CHASE, K.W. Statistical Tolerance Analysis of Compliant Assemblies with Polynomial Surface Covariance", ASME J. Mech. Des. 2005

TONKS, M. R., CHASE, K.W., SMITH, C.C. Predicting Deformation of Compliant Assemblies Using Covariant Statistical Tolerance Analysis, 9th CIRP Intl. Seminar on Computer-Aided Tolerancing, AZ, 2006.

WECKENMANN, A. 10th CIRP Conference on Computer Aided Tolerancing – CAT 2007, Measuring Science and Technology, 19 (2008) doi:10.1088/0957-0233/19/6/060101,

WITTWER, J.W., CHASE, K.W., HOWELL, L.L. The Direct Linearization Method Applied to Position Error in Kinematic Linkages, Mech. Mach. Theory, 39 (2004) 681-693.

WITTWER, J.W., CHASE, K.W., HOWELL, L.W. Predicting the Position Error in Kinematic Linkages: A Comparison of Deterministic and Probabilistic Methods, ASME Mechanism Conference, 2001.

YU, M.Q.; YAN, Y.; HAO, J.; WANG, G.X. A nonlinear tolerance analysis method using worst-case and Matlab. Adv. Mat. Res. 201-20 (2011) 247-252.

1 Professor do Centro Universitário Salesiano de São Paulo – UNISAL roderley@sj.unisal.br

2 Professor Titular do Programa de Pós Graduação em Engenharia de Produção da UNIMEP – Universidade Metodista de Piracicaba crclima@unimep.br