Espacios. Vol. 35 (Nº 11) Año 2014. Pág. 12
Programação Linear: Uma aplicação para a otimização na distribuição de uma empresa de nutrição animal
Heterogeneity of Brazilian agriculture in access to information technologies
Bianca Jupiara FORTES 1; Roberto Portes RIBEIRO 2; Felipe Martins MÜLLER 3
Recibido: 08/07/14 • Aprobado: 23/08/14
Contenido
2. Cadeia logística e de distribuição
5 Problemas de rede e roteirização
7 O modelo de roteiros elaborado
RESUMO: |
ABSTRACT: |
1. Introdução
A logística de distribuição em cadeias de suprimentos tem assumido importante papel na economia brasileira, fundamentando-se assim a preocupação em se estudar e buscar a melhor forma de desenvolver estas atividades nas empresas. Neste contexto, Fleury (2007) aponta que as organizações necessitam se adaptar às constantes mudanças econômicas, como globalização, aumento da concorrência, maiores exigências dos clientes, inserindo em seu ambiente as inovações tecnológicas, visando gerenciar de maneira mais eficaz as operações logísticas, otimizando seus recursos e reduzindo seus custos, assim como os de distribuição. Nesse sentido, conforme Oliveira (2005), as empresas tem a necessidade de buscar, através da melhoria dos processos das cadeias produtivas, a excelência na qualidade dos produtos, minimizando custos e evitando ao máximo os desperdícios.
Dada à relevância desta área, este estudo é resultante de um antigo problema referente aos altos custos do setor de logística de distribuição de uma empresa localizada ao norte do Estado do Rio Grande do Sul. Esse trabalho foi realizado por meio da investigação e análise de como ocorre o sistema de entregas juntamente à identificação de quais eram as demandas da região onde se realizavam tais entregas, buscando-se a elaboração de um modelo de roteirização para uma das regiões específica de distribuição de produtos desta empresa, objetivando-se reduzir seus custos.
A partir da solução apresentada da formação e análise dos roteiros a serem seguidos por cada caminhão da empresa na região em questão, busca-se levar a empresa uma proposta de diferencial nas entregas, minimizando custos, ampliando sua eficiência e consequentemente conferindo-lhe maior competitividade.
Pretende-se, portanto, verificar a relevância do estudo no setor de logística de distribuição para a empresa, aliado ao teste de eficácia da aplicação do método da pesquisa operacional, mais especificamente o modelo de elaboração de roteiros a ser apresentado. Para isso, o estudo é composto de cinco partes: introdução, referencial teórico, metodologia, modelo proposto e considerações finais.
2. Cadeia logística e de distribuição
Para uma empresa obter o melhor desempenho em um segmento, faz-se necessário inserir a gestão da cadeia logística. Conforme Ballou (2004) a missão da logística é dispor a mercadoria ou serviço certo, no lugar certo, no tempo certo e nas condições desejadas. Ao mesmo tempo em que fornece a maior contribuição à empresa, pois busca resultados superiores, alinhando todas as atividades de forma sincronizada para reduzir os custos.
Em termos conceituais faz-se relevante apresentar ainda o conceito de gestão da cadeia de suprimentos por Simchi-Levi et al. ( 2003):
O gerenciamento da cadeia de suprimentos é um conjunto de abordagens utilizadas para integrar de forma eficiente fornecedores, produtores, depósitos e lojas, de modo que o produto seja produzido, e distribuído nas quantidades certas, nos locais certos, de forma a minimizar s custos globais do sistema enquanto se satisfazem os níveis de serviços definidos (SIMCHI-LEVI et al., 2003, p. 18).
É importante considerar que diante da complexidade de um sistema logístico, deve-sefaz-se necessário analisá-lo em etapas, destaca-se assim o setor de distribuição, o qual é o foco desse estudo. Na linha de pensamento de Fleury (2007) desde a antiguidade, até os dias atuais, com avanço de tecnologias que permitem a troca de informações em tempo real, o transporte continua sendo fundamental para se atingir o objetivo logístico, ao menor custo possível. Tal que Ballou (2004) e Fleury (2007) afirmam que este setor ganha destaque, pois o transporte comumente representa para grande parte das empresas, o mais significante fator nos custos logísticos.
Para Figueiredo (2006) Bowersox e Closs (2004), a relevância da distribuição física está na integração que promove entre a empresa e seus clientes, sendo, portanto, um elo. E Figueiredo (2006) comenta que cada vez mais se apresentam exigências ao longo das cadeias, buscando maior eficiência e pontualidade nos serviços de entrega, melhor elaboração das rotas, melhor uso da frota e dos motoristas; gerando assim significativas reduções de custos operacionais, melhoria da imagem da empresa no mercado e consequentemente ampliando a fidelidade de clientes.
3. Transportes
Faz-se relevante discorrer mais especificamente sobre o setor de transportes, Ballou (2004) relata que a área de transporte dentro do gerenciamento logístico mostra-se de ampla importância, pois promove um diferencial tanto em níveis de serviço ao cliente quanto na estrutura de custo da organização.
Quanto à mensuração de custos, os princípios norteadores das operações e gerenciamento do transporte são dois, na concepção de Bowersox e Closs (2004): a economia de escala e a economia de distância. A primeira se dá por meio da redução dos custos de transporte por unidade de peso com cargas maiores e/ou consolidadas. Isso ocorre em virtude de que em economias de escala, as despesas fixas de transporte são diluídas quando há uma maior quantidade transportada. Já a economia de distância, é identificada pela redução dos custos de transporte por unidade de distância, à medida que ela aumenta.
O transporte rodoviário é aquele realizado em estradas de rodagem com a utilização de veículos, como por exemplo, caminhões e carretas, ou ainda em menor escala por veículos de menor porte. É considerado o modal mais flexível por possibilitar um serviço ponto a ponto, tornando possível o carregamento no estabelecimento de origem e a descarga no próprio armazém de destino, sem a obrigação de utilizar armazéns de terceiros (FRANZONI; FREITAS, 2005).
Para Bowersox e Closs (2004), as transportadoras rodoviárias necessitam de investimentos fixos, relativamente pequenos, em terminais que operam em rodovias com manutenção pública. Já os custos variáveis são considerados médios, no entanto, o custo variável por quilômetro é alto, sendo necessária uma unidade motora e um motorista para cada veículo despachado.
4. Pesquisa operacional
Conforme Oliveira (2005), a tomada de decisão tem grande relevância na atualidade, apresentando alta complexidade, principalmente quando se tem várias alternativas, onde cada decisão envolve fatores relevantes para os negócios das organizações. Nesta esfera, insere-se o campo da pesquisa operacional, considerado um método que oferece suporte ao processo decisório em organizações, tornando-o mais aprimorado, melhorando seu desempenho e elevando o nível de confiança na escolha feita.
A pesquisa operacional teve origem nos anos da Segunda Guerra Mundial, quando evidenciou a necessidade de se alocar os recursos escassos de maneira eficiente para otimizar as atividades militares que eram feitas. (HILLIER; LIEBERMAN, 2006; ARENALES et al., 2007; ANDRADE, 2004).
De forma mais específica a definição de pesquisa operacional é:
[...] Pesquisa operacional é a aplicação de métodos científicos a problemas complexos para auxiliar no processo de tomada de decisão, tais como projetar, planejar e operar sistemas em situações que requerem alocações de recursos escassos. (ARENALES et al. 2007, p. 6).
Atualmente ela oferece um mister de ferramentas que auxiliam no processo de tomada de decisões gerenciais, e os realiza por meio da formulação de modelos matemáticos, que podem ser executados com o auxílio de computadores. Goldbarg e Luna (2005) comentam que os modelos matemáticos que a pesquisa operacional permite elaborar podem-se dividir em dois grupos: programação linear (PL) e programação não-linear (PNL). E afirmam ainda que na PL as variáveis são ininterruptas e demonstram comportamento linear, no que se refere às restrições, e também à função objetivo, assim é vista como algo a parte dos modelos de programação matemática; e já os modelos PNL, tanto nas suas restrições como na função objetivo, demonstram qualquer forma de não-linearidade, em problemas de programação matemática. A técnica do Método Simplex é amplamente empregada, em razão de ter habilidade para modelar os complexos problemas de decisão, e aptidão de produzir soluções rapidamente, dependendo das particularidades do problema. O Método Simplex pode ter sua definição encontrada em Zionts (1974).
Os problemas de PL são compostos por:
- Uma função linear formada pelas variáveis de decisão, chamada de função objetivo, cujo valor deve ser otimizado;
- Relações de interdependência entre as variáveis de decisão que se expressam por um conjunto de equações ou inequações lineares, chamadas de restrições do modelo;
- Variáveis de decisão que devem ser positivas ou nulas;
As equações (1), (2) e (3) mostram a formulação para um problema de PL:
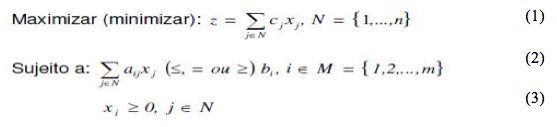
Com o surgimento da programação linear, em meados da década de 40, em destaque o modelo de transporte, foi possível inserir cenários mais complexos que o original. Assim viabilizando um meio de trabalhar com várias regiões de demanda, e também com várias regiões de oferta de matéria-prima. Segundo Nunes (2002), uma das vantagens de se trabalhar com modelos multiregionais é que ele consiste no fluxo de produtos e os preços relativos de mercado ao mesmo tempo.
5 Problemas de rede e roteirização
De acordo com Lachtermacher (2009) é comum que modelos de redes sejam aplicados à situações particulares de problemas de programação linear, sendo analisados por meio de uma representação gráfica. São inúmeros os problemas que permitem sua modelagem em redes, onde, associando informações de distâncias, custos ou tempos com demandas e capacidades de serviços, utiliza-se geralmente o conceito espacial.
Scarpin et al. (2010) comentam que uma rede de transportes, trabalhada em termos matemáticos é um grafo, sendo uma ferramenta acessível e eficaz, empregada no campo de pesquisa operacional, em problemas de roteirização, por exemplo. A teoria dos grafos, visa localizar facilidades ao longo de uma rede viária, o autor descreve o problema de agrupamento – clusterização, onde o problema das p-medianas será implementado para delinear no grafo formado pelos clientes, p-pontos principais, que representam depósitos fictícios. Sendo que o restante dos pontos serão determinados a cada uma destas medianas, para que se forme p-conjuntos iniciais cada um com cardinalidade igual à capacidade dos veículos. Salienta-se que estas facilidades ponderadas por um fator de demanda, necessitam ser localizadas visando à minimização da soma da distância de cada um dos pontos à facilidade mais próxima.
Os problemas de redes correspondem à variados problemas do mundo real, inclusive os problemas de menor caminho, o qual é analisado neste estudo, sendo considerado por Lachtermacher (2009) como a representação de um caso especial em que os arcos correspondem à distância entre dois pontos. No problema de rota mais curta, Lorena (2003) afirma que são diversos os algoritmos que podem ser usados, onde em cada arco de um grafo, determina-se a distância que representa. Possuindo como finalidade identificar o caminho mais curto entre dois nós e podem também ser úteis na descrição de custos ou tempos mínimos.
Já problemas de roteirização de veículos, introduzido por Dantzig e Ramser (1959), conforme Ballou (2004) é um dos problemas mais impactantes no custo logístico. E tem sua definição segundo Pileggi e Rosa (2006) como sequências de pontos de carregamento/descarregamento pelos quais os veículos deverão passar, ao custo mais baixo possível, respeitando todas as restrições do problema, inserindo-se as decisões, objetivos e restrições. Sendo as decisões, a alocação de um conjunto de veículos a um determinado grupo de clientes, pelos quais os veículos devem passar e a elaboração do sequenciamento dessas visitas. Já os objetivos consistem em maximizar o nível de serviço oferecido aos clientes e minimizar os custos operacionais. Nas restrições, as rotas devem ser com os recursos disponíveis, respeitando restrições de trânsito como o tamanho dos veículos e os limites de tempo dos motoristas.
Caric e Gold (2008) comentam em seus estudos que se pode conceituar o problema de roteamento de veículos (PRV) como dado um conjunto de n (i=1,..,n) clientes, onde cada um demandando uma quantidade qi de certo produto, e um armazém com m veículos de capacidade Q, a finalidade é tendo inicio e termino no depósito, identificar um conjunto de rotas, resultando no suprimento das demandas de todos os clientes, e que estes possam ser atendidos somente por um único veículo alcançando a minimização de custos de transporte. Perante essa eficácia na minimização de custos afirmam ainda que o problema do roteamento de veículos vem sendo um dos temas mais estudado em otimização combinatória nas últimas décadas.
6 Metodologia
O método empregado no trabalho conforme Vergara (2004) classifica-se quanto aos fins como exploratório por meio do qual, se realizou levantamento bibliográfico dos temas tratados no estudo, e descritivo, pois trabalha com dados colhidos da própria realidade, e nesse estudo foram coletados dados no departamento de contabilidade da empresa, ou seja, nos relatórios contábeis e nas notas de entrega, quanto a cada custo de quilômetros por litro dos caminhões e capacidade dos caminhões. Salienta-se que foi pesquisado o endereço de cada localidade de entregas, quantidade de pedido, data de pedido, além da distância em quilômetros da empresa até cada localidade de entrega. Utilizaram-se mapas e entrevistas não estruturadas com os motoristas da empresa para analisar as regiões onde estão localizados os mercados consumidores.
Além disso, essa pesquisa é de abordagem experimental e quantitativa, fez uso da técnica de modelagem matemática aplicando-se o método da pesquisa operacional, a qual evidencia alguns dados tratados como informações para serem analisados na tomada de decisão. Sampieri et al. (2006, p. 157) mencionam que "o método experimental remete diretamente a uma abordagem quantitativa e de modelagem empírico descritiva". Por fim empregou-se o programa computacional Microsoft Excel®, ressaltando-se que na criação do modelo foi utilizado o método de programação linear, usando o complemento do Solver desse software, o qual de acordo Lapponi (2005) é um comando que oferece uma resolução prática, para análise e execução de fórmulas tanto de maximização quanto de minimização, que é o caso aplicado neste estudo, pois se trabalhou com o fator de minimização dos custos das entregas.
7 O modelo de roteiros elaborado
7.1 Etapa de definição do problema, coleta e análise de dados
Para elaboração do modelo de roteiros foi necessário inicialmente, realizar um diagnóstico do setor de distribuição da empresa em questão, este foi descrito brevemente, oferecendo um melhor entendimento do problema abordado: A partir das observações na empresa estudada e entrevistas com o gerente de logística, com os agentes envolvidos na elaboração de notas para os pedidos das entregas aos clientes, foi possível chegar ao seguinte diagnóstico:
As entregas na empresa ocorrem de segunda a sábado, por meio de sua frota própria, esta é composta de onze caminhões, dentre estes sete são caminhões baú com a entrega de produtos ensacados e quatro são para a entrega de produtos a granel. Por ser a distribuição a granel a forma de entrega abordada neste estudo, vale salientar que dos quatro caminhões dois têm capacidade de vinte toneladas, e os outros dois de quinze toneladas.
O modo como ocorre o processo de entregas é diretamente aos revendedores e também diretamente a todos os clientes atendidos por cada revendedor. Não há redistribuição do produto a granel pelos revendedores, estes atuam apenas como intermediários entre cliente e empresa para negociações de compra e venda, pois a maior parte deles não possui silos em seus estabelecimentos para repassar ao produtor, somente alguns dispõem de pequenos estoques para reposição em casos de pedidos de emergências dos clientes ou atrasos nas entregas por parte da empresa. Evidenciando deste modo, a complexidade do atual sistema logístico da empresa estudada, na medida em que entrega diretamente a todos os seus clientes, nas mais diversas regiões em que estão alocados seus mercados consumidores incluindo os estados do Rio Grande do Sul e Santa Catarina. Agravando a complexidade de sua distribuição, a empresa atualmente não dispõe de um roteiro específico para entrega nas diferentes regiões onde estão localizados seus clientes, a fim de alinhar a entrega das mercadorias por região.
Visando minimizar os custos da viagem, os funcionários do setor buscam constantemente fechar cargas e transportar o máximo de produtos para uma mesma região, contatando o maior número de clientes possíveis para mandar uma carga fechada na região onde estão sendo solicitados os produtos, caso um pedido só, não ocupe toda a capacidade do caminhão. Fato esse, faz o serviço perder eficiência, gerando atrasos em mais de um dia para o fechamento e liberação de uma carga para seus locais de destino.
Esse cuidado em maximizar o preenchimento das cargas, procede dos altos custos que vem se apresentando há algum tempo no setor. Conforme a opinião dos revendedores e seus clientes a logística da empresa é percebida de modo positivo por ser de grande flexibilidade, porém para a empresa isso não vem se refletindo positivamente, pois, entregas realizadas sem planejamentos de periodicidades em uma região, resultam em altos custos de distribuição para a empresa, levando-a buscar uma solução para não repassar esse alto valor ao preço de venda dos produtos e ao mesmo tempo evitando prejuízos. Além disso, tais custos são tão expressivos que conforme os relatórios contábeis da empresa vêm sendo os maiores dentre os ouros setores, excedendo até mesmo o custo total de produção.
A partir desta avaliação do setor de distribuição, foi abordada a próxima etapa para a elaboração dos roteiros. Primeiramente por análise junto à empresa, determinou-se que, devido ao fluxo intenso de entregas a granel na região do extremo oeste de Santa Catarina, seria essa a região de entregas modelada. Mais especificamente formada por quatro cidades que serão aqui denominadas como Cidade A, Cidade B, Cidade C, Cidade D. Essa seleção procedeu do modo de entregas da empresa, como falado anteriormente, estas são realizadas diretamente à clientes localizados em linhas do interior, fato este que limitou a coleta de dados exata das quilometragens. Para simplificar o modelo, os clientes distribuídos nas variadas linhas do interior localizadas entre as quatro cidades (A, B, C e D) foram agrupados a partir de dois critérios, união daqueles pertencentes à mesma linha, (união das linhas) e aqueles que apresentavam número aproximado de distância em quilômetros até o centro de distribuição, neste caso, mesmo que as linhas pertencessem a munícipios diferentes, mas próximos um do outro, eram unidas por possuírem distâncias similares.
Desta forma, ficou estabelecido que o número de nós, ou seja, de localidades para formar o modelo seriam cinco, isto é, cinco agrupamentos de localidades diferentes (Figura 1). Em seguida realizou-se uma média da distância em Km do Centro de Distribuição da Empresa até cada uma das linhas que formaram cada um dos cinco agrupamentos (nós). Assim ficaram estabelecidas as médias das distâncias para cada nó da seguinte forma conforme se observa no modelo de rede representado na Figura 1: Nó 1 = 127 km; Nó 2 = 133 km; Nó 3 = 113 km; Nó 4 = 164,5 km; Nó-5 = 139,5 km.
Além disso, foram coletados no departamento de contabilidade, os dados quanto a cada custo de quilômetros por litros dos caminhões, a capacidade dos caminhões, onde os quatro caminhões empregados no modelo de entrega a granel possuem capacidades em toneladas e custos de combustíveis diferentes. Assim, são demonstrados na Tabela 1 os dados específicos de cada um dos caminhões e qual a sua denominação no modelo, visando uma melhor identificação.
Figura 1 – Modelo de Rede Elaborado

Fonte: (Elaborado pelos autores)
Quadro 1: Identifição dos caminhões no modelo elaborado

Parte da coleta de dados foi realizada por meio de todas as notas expedidas para todos revendedores da região selecionada, as quais apresentavam o endereço de cada localidade específica de entregas, quantidade de pedido (demanda por cliente), e a data de pedido vendido a cada cliente (frequência de pedidos por cliente) para o período de janeiro à outubro de 2013. Além da coleta da distância em quilômetros de cada localidade de entrega até a empresa (Figura 1). Tendo acesso a coleta de todos esses dados, foram então tabulados em planilha eletrônica (Microsoft Excel®), para a etapa de organização dos dados reais, e posterior emprego na elaboração do modelo de rede elaborado. Deste modo, depois de todos os dados tabulados e organizados, foram desenvolvidos os cálculos necessários visando obter as variáveis contidas no modelo:
- Média mensal de demanda por cliente;
- Frequência mensal de pedidos por cliente;
- Frequência mensal de pedidos (X) a demanda mensal média dos clientes;
- Soma das médias de demanda mensais (X) frequência de demandas por agrupamento de localidade;
- Média da distância em quilômetros de cada agrupamento de localidade até a empresa (Figura 1); e
- Custo de cada caminhão (Tabela 1) (X) média da distância em quilômetros de cada agrupamento de localidade até a empresa (Figura 1).
7.2 A Etapa para formulação do modelo matemático para representar o problema nálise dos dados obtidos
Para iniciar a modelagem do problema definem-se quais são as variáveis de decisão na função objetivo, as quais se referem com que frequência mensal cada caminhão irá para cada um dos nós, ou seja, os cinco agrupamentos de localidades (Figura1). O número de caminhões de entrega é quatro, cada um possuindo uma capacidade de carga em tonelada e custo de quilometro por litro diferente.
Assim, buscou-se os valores dessas variáveis de decisão que minimizem os custos (Equação 1), esses valores na alternativa selecionada devem satisfazer um conjunto de restrições.
As restrições, referem-se à quantidade de demanda por agrupamento, essa determinava que a soma das capacidades de cada caminhão deveria ser igual à soma da demanda de cada agrupamento (Equação 2) e (Equação 7 à 11).
E a outra restrição refere-se à limitação imposta no problema de que cada caminhão poderia fazer no máximo cinco viagens por mês para cada localidade, isto é para o mesmo lugar, tal quantia imposta a fim de otimizar o número de viagens que atendesse a demanda ao menor custo possível (Equações 3 e 4), juntamente, está imposto o trajeto de cada caminho, onde todas as constantes são cinco como exemplifica a Equação 12. Desta forma têm-se o modelo matemático:
Modelo matemático

Onde:
e = empresa
j = caminhão
p = localidade do produtor
Dpj = demanda da localidade do produtor p do caminhão j
Kep = distância da empresa e para entreposto k
Cej = custo da empresa e do caminhão j
oj = capacidade de carga do caminhão j
np = números de produtores
x = números de viagens dos caminhões.
7.2.1 A Função objetivo
A função objetivo teve sua formulação com o cálculo do custo de combustível por quilômetro percorrido de cada um dos quatro caminhões de entrega a granel da empresa, sendo que a média de cada custo foi calculada pelos dados apresentados do período de janeiro a outubro de 2013 (Tabela 1). Tais custos foram multiplicados pela média de quilômetros calculada para cada agrupamento de localidade, estas médias de km são aquelas apresentadas na Figura 1. As variáveis na função objetivo representam a quantidade de viagem mensal que cada caminhão faz de acordo com sua capacidade para cada agrupamento, no cálculo busca-se pela função de minimização, encontrar o melhor roteiro de entregas desses caminhões visando atingir o menor custo possível.
A multiplicação do custo de combustível por quilômetro percorrido de cada um dos quatro caminhões pela média de quilômetros para cada agrupamento de localidade pode ser verificada na Equação 5, após este cálculo efetuado, configurou-se uma função objetivo para ser aplicada no Solver, conforme a Equação 6.
Demonstração da Função objetivo:
Min Z = 2,57*127X11 + 2,82*127X12 + 2,47*127X13 + 2,52*127X14 + 2,57*133X21 + 2,82* 133X22 + 2,47*133X23 +2,52*133X24 + 2,57*113X31 + 2,82*113X32 + 2,47*113X33 + 2,52*113X34 + 2,57*139,5X41 + 2,82*139,5X42 + 2,47*139,5X43 + 2,52*139,5X4 + 2,57*164,5X51 + 2,82*164,5X52 + 2,47*164,5X53 + 2,52*164,5X54 (5)
Min Z = 326,3X11 + 358,14X12 + 313,69X13 + 320,04X14 + 342,81X21 + 375,06X22 + 328,51X23 + 335,16X24 + 291,7X31 + 320,07X32 + 280,34X33 + 286,02X34 + 358,51X41 + 393,39X42 + 344,56X43 + 351,54X44 + 422,76X51 + 463,89X52+ 406,32X53 + 414,54X54 (6)
7.2.2 Restrições
As restrições impostas ao problema referem-se à quantidade de demanda por agrupamento, essa determina que a soma das capacidades de cada caminhão deve ser igual à soma da demanda de cada agrupamento (Equação 7 à 11). A segunda restrição refere-se à limitação imposta no problema de que cada caminhão poderia fazer no máximo cinco viagens por mês para cada localidade, isto é, para o mesmo lugar, tal quantia foi imposta a fim encontrar o número de viagens que atendesse a demanda ao menor custo possível, a equação 12, exemplifica as estas cinco restrções.
Demonstração da Restrição 1:
15*X11+15*X12+20*X13+20*X14 = 53,43 (7)
15*X21+15*X22+20*X23+20*X24 = 60,59 (8)
15*X31+15*X32+20*X33+20*X34 = 56,59 (9)
15*X41+15*X42+20*X43+20*X44 = 32, 51 (10)
15*X51+15*X52+20*X53+20*X54 = 53, 34 (11)
Demonstração da Restrição 2:
1*X11+1*X12+1*X13+1*X14 ≤ 5 (12)
7.3 Desenvolvimento do procedimento computacional para implementação e resolução do modelo restrições
Na solução do problema desenvolvido em planilha eletrônica com o programa, o primeiro passo é a forma como devem ser organizadas as células na planilha, pois essa organização refletirá em toda a resolução do problema (Figura 3). Inicia-se colocando os parâmetros do modelo, sendo os custos de cada caminhão para cada localidade, vistos nas células B3 à U3, em seguida descrevem-se as variáveis de decisão, como são vinte neste caso, devendo ser distribuídas em vinte células, que receberão esses valores (B4 à U4), e uma para representar o valor que será atribuído à função objetivo (B5), sendo de minimização. Alocam-se as restrições, em cinco células, representando as constantes, limites impostos, (W9 à W17).
Nas células V9 à V17 serão expressos os valores totais de demanda atendida por localidade e quanto de viagens cada caminhão realiza, resultantes das restrições impostas. Nas células B9 à U17, é especificada a relação que cada um dos quatro tipos de caminhões por localidade tem com cada restrição. Em seguida, determina-se o modelo na ferramenta Solver com a janela de parâmetros sendo organizada como apresentado na Figura 1, definindo-se a restrição de não negatividade, no botão "Tornar variáveis irrestritas Não negativas" e para enquadrar o problema como uma aplicação de programação linear, clica-se na opção de método "LP Simplex".
Por fim, para otimizar o modelo clica-se no botão Resolver (Figura 2). E a partir da resolução podem ser observados os resultados em planilha eletrônica (Figura 3).
Figura 2 – Configuração do Solver do Programa Excel
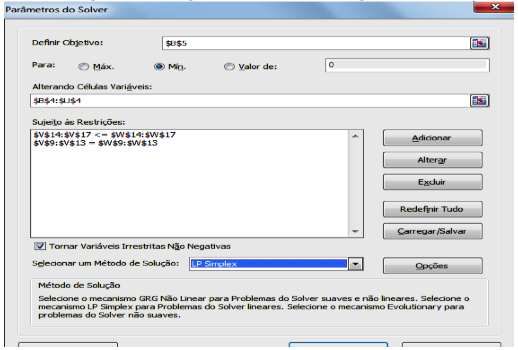
Fonte:( Elaborado pelos autores)
---
Figura 3 - Resolução do problema no Programa Excel

Fonte:( Elaborado pelos autores)
7.4 Análises dos resultados obtidos e validação do modelo
A partir da solução do problema, obteve-se a resposta de qual é a melhor quantidade, ou seja, a solução ótima de viagens de cada caminhão, adequando-se ao custo por caminhão e distância que cada local tinha, submetido às diferentes distâncias das localidades à empresa. Desta forma, os resultados foram os seguintes:
O caminhão tipo 4 do modelo, é o único que deve atender a demanda mensal da localidade um (Nó-1), o qual possui 20 toneladas para realizar estas entregas por meio de três viagens por mês. Já o agrupamento ou nó dois deve receber entregas do caminhão 3 e 4, os quais devem fazer uma e duas viagens mensais para suprir sua demanda respectivamente. No que diz respeito ao agrupamento 3, esta deve receber entregas apenas do caminhão 4 o qual possui 20 toneladas, e ele realizará três viagens mensais para este local. Já o agrupamento da localidade quatro deve receber ofertas somente do caminhão 3, este de 20 toneladas, o qual necessitará realizar duas viagens para estes locais. E por fim, o agrupamento de localidade cinco receberá produtos apenas do caminhão tipo 3, este de 20 toneladas que suprirá toda a demanda por meio de três viagens.
Deste modo, o resultado evidencia que é necessário ter-se um número de viagens determinado para cada caminhão com antecedência, visando à minimização dos custos, assim como observado nos resultados, este a partir da aplicação no problema do roteiro de entregas dos caminhões por local e demanda. Assim, observa-se nos resultados, uma função objetivo minimizada ao valor de R$ 4.611,00, representando atingir a minimização dos custos no período de um mês para essas linhas atendidas, já que se realizou uma simulação de entrega conforme a demanda mensal da região. Salienta-se que se elaborou também outra resolução como teste, com a limitação de quatro viagens e o resultado apresentou custos maiores, incluindo-se nas entregas o caminhão tipo 2, o qual tem o maior custo. Assim, na medida em que se incluíram cinco viagens limitando o problema, esse caminhão foi eliminado automaticamente pelo modelo.
De acordo com a região estudada, afirma-se que o roteiro mensal estabelecido por agrupamento pode ser elaborado da seguinte forma:
- Nó 1 - três viagens, nos dias 5, 12, 19, entregues pelo caminhão tipo 4;
- Nó 2 - três entregas, nos dias 10, 20 e 30, entregues por dois caminhões (tipo 3 e 4);
- Nó 3 - quatro entregas, nos dias 1, 11, 21 e 31, todas realizadas pelo caminhão tipo 1;
- Nó 4 - duas entregas, apenas do caminhão tipo 3, nos dias 17 e 28; e
- Nó 5 - três viagens, nos dias 5, 14 e 24, todas pelo caminhão tipo 3, visando-se estar atento para não confrontar as viagens com o nó 2 e 4 que também recebem desse caminhão.
Observou-se que os caminhões mais solicitados pelo problema para as entregas, realizando o máximo de viagens possíveis foram os caminhões que apresentavam os menores custos, o caminhão tipo 3 (R$ 2,47) e o caminhão tipo 4 (R$ 2,52), e em seguida o caminhão tipo 1 com quatro viagens, o terceiro de menor custo no modelo (R$ 2,57). Ressaltando novamente o fato do caminhão tipo 2 não ter sido direcionado para nenhuma viagem, por ter o maior custo (R$ 2,82), mostrando que empresa poderia deixar de empregar esse caminhão no seu processo de distribuição. O uso dos roteiros, mostra que alocando os caminhões entre os lugares através de mais viagens por mês na medida em que retira um dos seus caminhões, otimiza as suas entregas e reduz seus custos.
Mostra-se relevante ainda o modelo de roteiros elaborado, pois além de reduzir os custos de combustível abordado no problema, também reduzirá os custos fixos com a utilização de um caminhão a menos em sua frota, reduzindo consideravelmente os custos com o setor de transportes. Por outro lado, verifica-se assim, que não necessitará repassar custos mais altos ao produto final, mantendo os preços atuais, conservando seus clientes e ainda com esse diferencial na sua logística de distribuição, há maior viabilidade de ampliar seu mercado consumidor. Sendo que consequentemente uma redução de custos aliado a mais vendas, otimizará sua receita e seus lucros.
Por fim, o modelo de redes elaborado se mostra eficaz também, pois como demonstrado na resolução do problema, todas as demandas são atendidas. Assim, corresponde plenamente à expectativa contida no pedido de compra do cliente, e ainda regulamenta as datas de entregas, com a fixação destes dias, proporcionado aos clientes à oportunidade de aguardar chegadas dos produtos na data certa, evitando contratempos e maximizando sua satisfação.
8 Conlusões
Os reflexos das transformações da economia vêm ocorrendo em todos os setores, assim a velocidade e a competência com que esta realidade é assimilada pelas empresas constituem um diferencial que pode determinar a sua evolução ou a sua exclusão do mercado. Para tanto, a partir de uma análise do setor de logística de uma empresa, pode-se elaborar um modelo de roteiros de entregas de produtos nas regiões de seus mercados consumidores no extremo oeste de Santa Catarina, visando minimizar os custos da empresa.
O estudo alcançou seus objetivos, pois a partir de um embasamento teórico, juntamente ao levantamento de dados, elaborou-se um modelo de roteiro, demonstrando a eficácia da redução de custos de transportes por meio do método da pesquisa operacional, esta aplicada à realidade da empresa. Onde se obteve a minimização dos custos com atendimento de toda a demanda, porém com uma frota menor de caminhões, eliminando-se o caminhão no processo apresentava os maiores custos no processo, chegando-se ao resultado ótimo de R$ 4.611,00, para o atendimento mensal da região estudada. Evidenciando, assim a necessidade de inserir esse diferencial na logística de distribuição, pois reduz custos e organiza as suas entregas, tornando-se positivo também para o consumidor caso essa redução de custos seja factível com uma redução no preço de venda dos produtos.
Verificou-se, portanto, que se implementados tais roteiros na empresa, utilizar-se-iam três dos quatro caminhões que compõe sua frota a granel, esses com menores custos de rodagem, com uma quantia de viagens que atenderia todas as demandas mensais apresentadas por cada localidade, otimizando suas entregas, e ao mesmo tempo reduzindo seus custos.
Por meio do problema proposto evidencia-se a relevância da Pesquisa Operacional como ferramenta importante na tomada de decisão dos gestores, com destaque ao método de elaboração de roteiro para minimização dos custos logísticos de distribuição das organizações. Desse modo, compreende-se que a programação linear, técnica empregada no modelo, auxilia na minimização de custos, bem como, na maximização do lucro da empresa que faz uso de tal metodologia. Logo, a utilização deste método no presente estudo permite inferir a existência de diversas possibilidades de aplicação da Pesquisa Operacional, aqui vista como ferramenta de melhoria no desempenho de uma cadeia de distribuição.
Por fim, o trabalho encontrou como limitação o amplo número de clientes que a empresa entrega seus produtos, simplificando a aplicação do modelo em apenas uma das regiões, em razão da coleta de dados ser de grande complexidade para formulação do modelo. Sugere-se a empresa, a divisão de regiões de entrega como realizado no estudo, para obter maior controle da quantidade de demanda e distâncias, simplificando a elaboração de roteiros, sendo viável atender melhor à menor custo.
Referências Bibliográficas
ANDRADE, E. L. Introdução a Pesquisa Operacional: métodos e modelos para análise de decisão. 3. ed. Rio de Janeiro: LTC, 2004.
ARENALES, M. ARMAMENTO, V.; MORABITO, R. & YANASSE, H. Pesquisa Operacional – para cursos de Engenharia. Rio de Janeiro: Elsevier, 2007.
BALLOU, R. H. Gerenciamento da Cadeia de Suprimentos. 5. ed. Porto Alegre: Bookman, 2004.
BOWERSOX, D. J. & CLOSS, D. J. Logística Empresarial: o processo de integração da cadeia de suprimento. São Paulo: Atlas, 2004.
CARIĆ, T. & GOLD, H. Vehicle Routing Problem. In-Teh, Zagreb, 2008.
FRANZONI, A. M. B & FREITAS, S. M. M. Logística de Transporte Internacional. In: SIMPÓSIO NACIONAL DE ENGENHARIA DE PRODUÇÃO, 12., 2005, Bauru. Anais... Bauru: SIMPEP, 2005.
FIGUEIREDO, K. A Logística Enxuta. 2006. Disponível em <http://joomla.coppead.ufrj.br/port/index.php?option=com_docman&task=cat_view&gid=56&Itemid=204&mosmsg=Voc%EA+est%E1+tentando+acessar+de+um+dom%EDnio+n%E3o+autorizado.+%28www.google.com.br%29>. Acesso em: 15 dez. 2013.
FLEURY, P. F. Logística e Transportes. Jornal Valor Econômico, São Paulo, ano 7, nº1673, p. A8, 9 jan. 2007.
GOLDBARG, M. C. & LUNA, H. P. L. Otimização Combinatória e Programação Linear: Modelos e algoritmos. 2. ed. Rio de Janeiro: Campus, 2005.
HILLIER, F. S. & LIEBERMAN, G. J. Introdução à Pesquisa Operacional. 8. ed. São Paulo:McGraw-Hill, 2006.
LACHTERMACHER, G. Pesquisa Operacional na Tomada de Decisões. 4. ed. São Paulo: Pearson Prentice Hall, 2009.
LAPPONI, J. Estatística Usando o Excel. 4. ed. Rio de Janeiro: Campus Elsevier, 2005.
LORENA, L. A. N. Análise Espacial de Redes com Aplicações em Sistemas de informações Geográficas. 2003. Disponível em: <http://www.lac.inpe.br/~lorena/producao/Analiseredes.pdf>. Acesso em: 09 out. 2013.
NUNES, L. F. Um algoritmo heurístico para a solução de problemas de grande escala de localização de instalações com hierarquias. 2002. Tese (Doutorado em Engenharia de Produções) - Departamento de Engenharia de Produção. Universidade Federal de Santa Catarina, Florianópolis 2002.
OLIVEIRA, A. L. R.. Otimização de Recebimento e Distribuição em Unidades Armazenadoras de Soja. 2005. Dissertação (Mestrado em Ciências ) -Programa de Pós-Graduação em Métodos Numéricos em Engenharia, Área de Concentração em Programação Matemática dos setores: de Ciências Exatas e de Tecnologia da Universidade Federal do Paraná., Curitiba 2005.
PILEGGI, G. C. F. & ROSA, R. O. Avaliação da Logística de Distribuição de Produtos em uma Empresa de E-commerce. In: SIMPÓSIO NACIONAL DE ENGENHARIA DE PRODUÇÃO, 13., 2006, Bauru. Anais... Bauru: SIMPEP, 2006. p.1-12.
SAMPIERI, R. H.; COLLADO, C. F. & LUCIO, P. B. Metodologia de Pesquisa. 3. ed. São Paulo: McGraw-Hill, 2006.
SIMCHI-LEVI, D.; KAMINSKY, P. & SIMCHI-LEVI, E. Designing and Managing the Supply Chain: concepts, strategies and case studies. 2 ed., 2003.
VERGARA, S. C. Projetos e Relatórios de Pesquisa em Administração. 5. ed. São Paulo: Atlas, 2004.
ZIONTS, S. Linear andIntegerProgramming. Prentice-Hall, Inc, Englewood Cliffs,New Jersey, United States of America, 1974. http://www.irati.pr.gov.br/municipio/localizacaogeografica.asp - Página Prefeiruta Municipal de Irati, acessada em 05/12/2013.
1 (PPGEP/UFSM) Brasil. bifortes22@gmail.com
2. (USP/UFSM) Brasil. robertor@smail.ufsm.br
3. (PPGEP/UFSM) Brasil. felipe@inf.ufsm.br