1. Introdução
As organizações estão inseridas em um ambiente competitivo, constituído de clientes cada vez mais exigentes e concorrentes mais aguerridos. A busca por um desempenho melhor, num cenário como este, se faz necessária a todos aqueles que pretendem se manter e evoluir no mercado. Por isso, o gerenciamento financeiro é primordial para a saúde das empresas e peça chave para dar subsídio para o administrador ter a capacidade de tomar decisões corretas e rápidas no momento certo sem fugir das metas estabelecidas. A incorporação de técnicas contábeis e modelagens matemáticas auxiliam gestores a aprimorar a gestão financeira e produtiva permanecendo inovadores e atuais frente ao mercado cada vez mais tecnológico (TELÓ, 2001).
Um dos principais instrumentos para a análise financeira de qualquer empresa é o fluxo de caixa, pois possibilita um gerenciamento adequado dos recursos financeiros, evita a falta de liquidez e o não cumprimento dos compromissos, ou seja, disponibiliza a independência financeira da empresa (SILVA; SANTOS; OGAWA, 1993). A tomada de decisão por parte do proprietário precisa ser baseada na realidade do fluxo de caixa da empresa para que não haja descontrole entre receita e despesa. Ao fazer a sua projeção devem ser consideradas as entradas de recursos - como as contas a receber, os empréstimos e o capital investido pelos sócios - e as saídas de recursos - como: contas a pagar, despesas gerais da administração, que são os custos fixos da empresa, compras à vista e pagamento de empréstimos (FERRAZA; RAUBER, 2008).
O resultado em uma atividade significa se o empreendimento esta dando ao produtor lucro ou prejuízo. Serve para o produtor analisar sua empresa no longo prazo. Para calcular o resultado da atividade utiliza-se a seguinte expressão: Resultado: receita bruta – custo total (FUGI, 2004). É comum a utilização do diagrama de fluxo de caixa para tornar o processo visualmente mais fácil e entendível, já que, dá a noção do valor no tempo. O diagrama é composto por uma escala de tempo, uma reta horizontal, em intervalos contínuos e flechas verticais representando as saídas e entradas de recursos. O resultado da operação desses valores pode ser considerado uma série temporal. Série temporal é um conjunto de observações dispostas ao longo do tempo (MORETTIN, TOLOI, 1986).
A análise dessas séries tem por objetivo estudar sua trajetória ao longo do tempo, suas características, causas, efeitos e formas de controle. De posse dessas informações é possível modelar o fenômeno considerado. Buscando auxiliar o gerenciamento das informações financeiras o presente artigo utiliza a análise estatística descritiva para explorar as contas de uma empresa X do ramo gráfico, bem como estudar o comportamento das séries de receitas e despesas através da metodologia Box Jenkins e realizar previsões.
2 Histórico da Gráfica
A Gráfica foi fundada em 2004 e possui 14 funcionários, está localizada na região noroeste do estado do Rio Grande do Sul. Os serviços oferecidos são criação, design e diagramação de materiais comerciais, editoriais e industriais, pré-impressão, impressão em todos os tipos e gramaturas de papéis, acabamentos como corte, vinco, dobra, colagem, plastificação, grampo, intercalação, dentre outros.
Os produtos impressos na gráfica são revistas, livros, jornais, calendários, convites diversos, cartões, panfletos, sacolas de papel, cartazes, caixas de papel, blocos e materiais diversos. As máquinas utilizadas são computadores com softwares variados, CTP (Computer top late) pré-impressão, máquinas impressoras off set, impressoras digitais, guilhotinas, dobradeira, caldeira, corte e vinco, grampeadeira, plastificadora, serrilhadeira e seladora para embalagens.
A gráfica apresenta papel importante para a região e comunidade local e regional, na geração de renda, empregos e tributos, respeito ao meio ambiente, produtos e serviços oferecidos com tecnologia de ponta, mão de obra qualificada, prazo e preços justos.
É uma das poucas empresas do ramo com certificação de preservação do meio ambiente (selo verde), e atualmente está ampliando e diversificando os produtos oferecidos, com impressão em materiais flexíveis e bobinas para atender a demanda de rótulos e embalagens em diversos substratos.
Possui como diferencial das demais gráficas locais e regionais a tecnologia avançada à preservação do meio ambiente, formatos de impressão diferenciados, preços compatíveis e justos, em relação à qualidade dos produtos e serviços oferecidos.
3 Metodologia
Este estudo utiliza 49 dados mensais do balanço financeiro de uma empresa do ramo gráfico, do período compreendido entre os meses de março de 1998 a março de 2012. As séries utilizadas são referentes as receitas e despesas obtidas no período, com a finalidade de proporcionar subsídios que auxiliem na gestão e na tomada de decisão. De posse das informações coletadas junto a empresa é possível uma análise estatística descritiva e a aplicação do modelo estatístico de Box Jenkins com o auxílio dos softwares SAS 9.1. e Eviews 8 SV.
Para a análise estatística descritiva são realizadas as médias mensais dos anos, sendo que cada mês representado corresponde à média de 4 anos. Após a análise descritiva os dados são submetidos à aplicação da metodologia de números índices de base fixa, tendo como base março de 2008 à fevereiro de 2009, nesta etapa as variáveis foram consideradas isoladas, sem se calcular as médias dos meses em relação aos anos. Os procedimentos estatísticos foram realizados pelo programa SAS 9.1.
Os dados obtidos da empresa foram às receitas e às despesas, divididos por:
1. Receitas
1.1. Receita de vendas (RV)
1.2. Outras receitas (OR)
Obtendo um total de receitas = (RV+OR) e as despesas:
2. Despesas
2.1. Despesas de administração (DADM)
2.2. Despesas pessoais (DP)
2.3. Despesas comerciais (DC)
2.4. Despesas impostos (DI)
2.5. Despesas financeiras (DF)
2.6. Despesas produção (DPR)
2.7. Despesas não operacionais (DÑO)
Obtendo um total de Despesas = (DADM+DP+DC+DI+DF+DPR+DÑO)
O Lucro conforme relata Fugi (2004) é obtido através da subtração entre as receitas e as despesas.
Através do uso do software Eviews 8 SV é aplicada aos dados a metodologia de Box Jenkins. Esta metodologia é frequentemente usada para analisar modelos paramétricos. O procedimento consiste em um modelo matemático que capta o comportamento e a autocorrelação da série para realizar previsões futuras.
O modelo de Box e Jenkins (1994) tem como estratégia para a seleção do melhor modelo a ser aplicado à série o ciclo iterativo (SOUZA, CAMARGO, 1996). Este ciclo parte de duas ideias fundamentais, a parcimônia e a iteração entre suas fases. A parcimônia consiste na utilização do menor número de parâmetros possíveis para estabelecer o modelo matemático, e a iteração é a repetição da ação tantas vezes quanto necessário.
As fases do ciclo podem ser descritas na Figura 1, segundo Box, Jenkins e Reinsel (1994):
Figura 1: Etapas da abordagem interativa para a construção do modelo
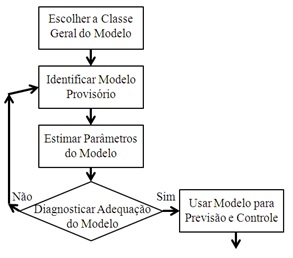
Fonte: Adaptado de Box, Jenkins e Reinsel (1994, p.17)
A iteratividade deste inicia a partir do item 4 do ciclo, pois ao ser diagnosticado que o modelo não é o melhor a ser utilizado é necessário retornar ao item dois e recomeçar a atividade (MORETTIN, TOLOI, 1986).
A identificação do modelo pode ser feita através da análise da função de autocorrelação – FAC e da função de autocorrelação parcial – FACP, a estimação dos parâmetros é feita após a identificação do modelo e efetua-se a avaliação dos resíduos gerados.
A modelagem Box Jenkins significa o ajuste dos modelos auto-regressivos de médias móveis ARIMA(p,d,q) em um conjunto de dados. A vantagem da utilização destes modelos é a parcimônia do método e a precisão das previsões em relação a outros modelos. No entanto, a desvantagem da aplicação é a necessidade de um conhecimento inicial da técnica por parte do aplicador, além do uso do pacote do computador.
Para o desenvolvimento de um ARIMA(p,d,q) são necessária, em torne de, 50 observações de uma série temporal yt, com mesmo intervalo de tempo entre as observações e esta deve ser estacionária. E estacionariedade de uma série se dá a medida que a média, a variância e a covariância se apresentam constantes ao longo do período. Para séries não estacionárias a aplicação do processo de diferenciação pode excluir os processos de não linearidade ou altamente explosivos. Segundo Macerau (2009) a maioria das análises de séries temporais pressupõe que as mesmas sejam estacionárias, no entanto, séries financeiras não apresentam esse comportamento.
A aplicação desta diferença consiste na diminuição da segunda observação pela primeira conforme a fórmula ∆dy = yt – yt-1, o valor diferenciado é igual ao valor de y no período t – 1, representado por d. A segunda diferença é dada por ∆dy = yt-1 – yt-2, d = 2. Tornar a série estacionária significa garantir que ela será estável ao longo dos períodos observados e assim o modelo estimado se torna representativo (SOUZA, CAMARGO, 1996). A diferenciação representa a parte I(d) do modelo ARIMA e deve ser evitada a sua aplicação mais de duas vezes na mesma série.
A parte auto-regressiva AR(p), de ordem p é explicada por yt = φ1 yt-1 + φ2 yt-2 + ... + φp yt-p.+ εt, na qual φ indica os parâmetros reais e εt o ruído branco. O ruído branco é um conjunto de variáveis aleatórias distribuídas de forma idêntica e possui a média dos valores é igual a zero, e a variância constante. O p pode ser conseguido através da análise do gráfico da FACP, a quantidade de parâmetros que estiver acima do intervalo de confiança determinado será o valor máximo.
O processo de médias móveis MA(q) segue a equação yt = εt – θ1 εt-1 –...– θq εt-q. O θ sugere as constantes reais e εt o ruído branco. A parte q, por sua vez, consegue-se pela análise do gráfico da FAC e assim como a parte p, a quantia de valores que estiver acima do intervalo irá determinar o máximo valor.
A equação completa do modelo ARIMA(p,q,d) é obtida através da composição das equações das partes AR(p) e MA(q) conforme segue: ∆dy = φ1 yt-1 + φ2 yt-2 + ... + φp yt-p.+ εt – θ1 εt-1 –...– θq εt-q (MORETTIN, 2008). Dos modelos encontrados para a ordem (p,q,d) passa-se à estimação da combinação dos possíveis. Os critérios que devem ser obedecidos são, por exemplo, o nível de significância inferior a 5%, p<0,05, a presença de ruído branco, Akaike (AIC – Akaike Information Criteria) e Bayes (BIC – Bayesian Information Criteria), os dois últimos servem para verificar qual modelo é aceitável através das equações AIC= lnσe2 + (2(p + q))/n e BIC = lnσe2 + ((p + q)lnn)/n; em que p e q são os parâmetros conhecidos, n é o tamanho da amostra, ln é o logaritmo neperiano e σe2 a variância estimada dos erros.
Os valores de AIC e BIC, obtidos dos diferentes modelos encontrados, são confrontados com o intuito de encontrar respectivamente os menores. Ou seja, quanto menor for o resultado do cálculo destes critérios mais adequado será o modelo para a projeção dos valores futuros da série em estudo.
4 Resultados e Discussões
Nas tabelas 1 (A) e 1 (B) é apresentado um resumo estatístico descritivo, contendo as principais medidas de onde se tomará base para fazer as analises.
Tabela 1 (A): Estatística descritiva do balanço financeiro no período de março de 2008 a março de 2012.
Variáveis |
Média |
Mínimo |
Q1 |
Mediana |
Q3 |
Máximo |
RV |
56190,0 |
7096,0 |
30361,0 |
53452,0 |
69005,0 |
214841,0 |
OR |
28718,0 |
2,0 |
1631,0 |
19345,0 |
36327,0 |
280000,0 |
DADM |
3847,0 |
42,0 |
1049,0 |
2823,0 |
5407,0 |
16172,0 |
DP |
15242,0 |
2479,0 |
10025,0 |
13238,0 |
18623,0 |
40663,0 |
DC |
1770,0 |
74,0 |
430,0 |
770,0 |
2113,0 |
10818,0 |
DI |
1693,0 |
0,0 |
202,0 |
289,0 |
953,0 |
25655,0 |
DF |
18178,0 |
35,0 |
6719,0 |
13089,0 |
25312,0 |
118465,0 |
DPR |
24968,0 |
1079,0 |
12939,0 |
19707,0 |
31308,0 |
73094,0 |
DÑO |
20221,0 |
300,0 |
6377,0 |
8027,0 |
16710,0 |
245145,0 |
Em que: RV = Receita de vendas; OR = Outras receitas; DADM = Despesas de administração; DP = Despesas pessoais; DC = Despesas comerciais; DI = Despesas impostos; DF = Despesas financeiras; DPR = Despesas produção; DÑO = Despesas não operacionais; n= número de observações (meses); Q1 = primeiro quartil; Q3 = terceiro quartil; CV%= coeficiente de variação em porcentagem.
Tabela 1 (B): Estatística descritiva do balanço financeiro no período de março de 2008 a março de 2012.
Variáveis |
Assimetria |
Curtose |
CV% |
Desvio padrão |
N |
RV |
1,75 |
5,84 |
65,6 |
36864,0 |
49 |
OR |
3,91 |
16,94 |
172,8 |
49619,0 |
49 |
DADM |
1,49 |
2,20 |
99,0 |
3806,0 |
49 |
DP |
1,17 |
1,77 |
51,5 |
7851,0 |
49 |
DC |
2,53 |
7,26 |
128,4 |
2274,0 |
49 |
DI |
4,45 |
20,20 |
272,3 |
4611,0 |
49 |
DF |
3,17 |
14,95 |
105,5 |
19176,0 |
49 |
DPR |
1,03 |
0,75 |
72,6 |
18119,0 |
49 |
DÑO |
4,55 |
23,97 |
192,6 |
38940,0 |
49 |
Em que: RV = Receita de vendas; OR = Outras receitas; DADM = Despesas de administração; DP = Despesas pessoais; DC = Despesas comerciais; DI = Despesas impostos; DF = Despesas financeiras; DPR = Despesas produção; DÑO = Despesas não operacionais; n= número de observações (meses); Q1 = primeiro quartil; Q3 = terceiro quartil; CV%= coeficiente de variação em porcentagem.
Conforme observado na Tabela 1, as medidas de dispersão expressas pelo coeficiente de variação de Pearson e pelo desvio padrão, na variável despesa com impostos foi obtido um valor extremamente alto de 272,3, o que mostra que a média das despesas com impostos não é representativa. Esta variável apresentou um desvio padrão de 4611,0, esta variabilidade é corroborada por um valor mínimo de despesas com impostos no valor igual a 0. Analisado as despesas não operacionais por meio dos mesmos critérios obteve-se um coeficiente de variação de 192,6 e um desvio padrão de 38940,0.
A analise descritiva por meio da Figura2, que representa o "boxplot" referente as receitas médias ao longo dos quatro anos (por mês) evidenciou que os meses de maior receita no período dos quatros anos avaliados foram obtidos nos meses de julho e dezembro de todos os anos.
Figura 2: receitas mensais no período de março de 2008 a fevereiro de 2012.
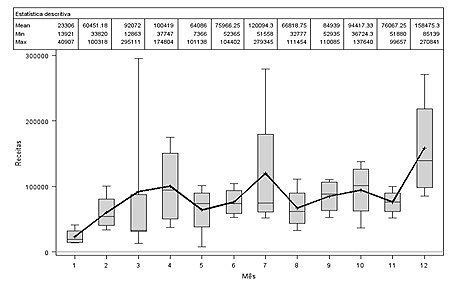
Porém verifica-se que nos meses de março, julho e dezembro de todos os anos são os meses que possuem maior variabilidade, correspondente a conta "outras receitas", conforme apresentado na Tabela 1.
Figura 3: despesas mensais no período de março de 2008 a fevereiro de 2012.
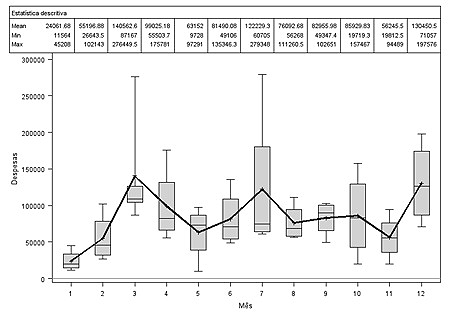
As despesas médias mensais no período correspondente ao mês 4 observadas na Figura 3 representada pelo "boxplot", vê-se que nos meses de março, julho e dezembro alcançou em média os maiores valores correspondendo a valores nominais de R$140.562,60, R$122.229,30 R$ 130.450,50; respectivamente. Entre as sete variáveis analisadas como despesas, os que tiveram maior variabilidade foram às despesas com impostos (DI) e despesas não operacionais (DÑO).
Figura 4: Boxplot do Lucro líquido mensais no período de março de 2008 a fevereiro de 2012.

A análise descritiva da Figura 4, observa-se que a empresa possui o seu maior prejuízo no mês de março. Esta queda pode estar associada ao mês em que paga-se mais impostos. Há uma oscilação entre lucro e prejuízo, tendendo esta diferença a se estabilizar entre um período e outro, começando a ter um lucro médio a partir do mês de setembro.
Figura 5: distribuição de porcentagem em função do lucro líquido no período de marco de 2008 a fevereiro de 2012.
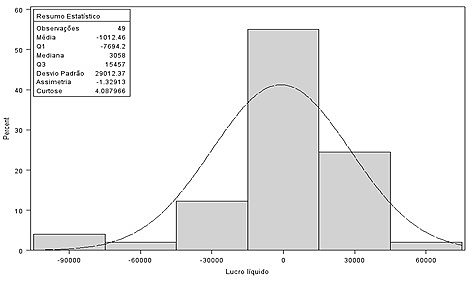
A Figura 5, referente a distribuição de porcentagem em função do lucro líquido, de acordo com o resumo estatístico avaliando as medidas de tendência central, verifica-se que através da mediana a empresa esta tendo no período considerado um lucro de R$ 3.058,00 ao mês, em oposição quando avaliado através da média a mesma possui um prejuízo de R$ 1.012,46.
A distribuição da função lucro líquido é assimetria à negativa com valor de-1,32913 e apresenta valores para a curtose de 4,08, a análise também indicou que a distribuição é platicúrtica. Analisando-se o excesso de curtose k - 3 = 4,08 – 3 = 1,08, indicaria que há uma volatilidade implícita nos dados, o que no futuro quando se proceder uma modelagem destas variáveis, deve-se investigar a presença de modelos heteroscedásticos, também esta modelagem deve ser considerada dado que o desvio padrão do lucro líquido é de 29012,37, o que é considerado elevado.
Figura 6: Comportamento dos números índices mensal usando como referência o primeiro ano
da empresa gráfica (marco de 2008): (a) Receitas; (b) Despesas; (c) Lucro líquido.

De acordo com a Figura 6 (a), onde foram calculados os números índices mensais tomando como base o primeiro ano do balanço da empresa (2008), com o intuito de verificar o desempenho destas variáveis ao longo do tempo. O ano de 2009 foi o que apresentou maior oscilação, sendo que nos anos posteriores houve um comportamento semelhante. Os meses que tiveram picos máximos foram os meses de abril (2009 e 2011), julho e dezembro (2009), fevereiro (2010) e o mês de março teve uma proporção do índice quase nula em todos os períodos.
Os números índices calculados para as despesas são mostradas na Figura 6 (b), onde observa-se um alta variabilidade (em torno de 300%) com ano base 2008.
Tomando como base o ano de 2008 a empresa no primeiro semestre manteve-se na sua maioria em prejuízo, a partir do segundo semestre a maioria dos meses apresentaram lucro, exceto no mês de setembro de 2009.
O estudo da metodologia Box Jenkins foi dividido em duas partes, a primeira refere-se a aplicação do modelo Box e Jenkins na série que representa as Receitas (R) obtidas pela gráfica durante os quatro anos observados. A segunda parte recebe o mesmo tratamento, mas para a série das Despesas (D01). Na Figura 7 é possível observar o gráfico da série original (R) das receitas e a mesma após uma diferenciação (D(R)).
Figura 7 – Gráfico da Série original das Receitas e Série diferenciada

Analisando a Figura 7 é possível identificar que a série original varia bastante em relação a média, por isso, foi aplicada uma diferenciação que a tornou estacionária.
Após tornar a série estacionária foram feitos os gráficos da FAC e FACP da série R para proceder à análise. De acordo com a FAC, há até dois lags que chegam ao limite do intervalo de confiança indicando a possibilidade da existência da parte de médias móveis – q. Na FACP identifica-se um lag acima do intervalo de confiança demonstrado a possibilidade do valor 1 para a parte autoregressiva - p, ou seja, de acordo com a análise prévia destes gráficos o provável modelo poderá ser ARIMA(1,1,1) ou ARIMA(1,1,2).
A partir das informações obtidas, a próxima etapa é a definição do modelo. Dentre os modelos aplicados, e através da análise dos critérios AIC e BIC, aquele que melhor representa a série R é o ARIMA(1,1,1) que é significativo ao nível de 5% (p<0,05).
O estudo dos resíduos comprova a validade do modelo, já que, apresenta ruído branco e os resíduos quadráticos indicam que o modelo não é ARCH. A Figura 8 representa a previsão estipulada pelo modelo, que pode ser expressa pela equação: ARIMA(1,1,1): ŷt = - 0,312157. yt-1 – 0,924307.εt-1 + εt.
Figura 8 – Previsão do modelo ARIMA(1,1,1)
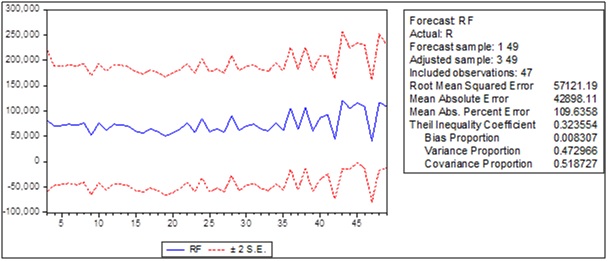
Na Tabela 2 têm-se as previsões de receitas para o próximo semestre da gráfica.
Tabela 2 – Previsões de Receitas
Mês |
yt |
Previsão |
Abril/12 |
50 |
121420,0 |
Maio/12 |
51 |
92701,2 |
Junho/12 |
52 |
101870,1 |
Julho/12 |
53 |
98942,8 |
Agosto/12 |
54 |
99877,4 |
Setembro/12 |
55 |
99579,0 |
A segunda etapa do artigo segue a mesma metodologia e organização da primeira entretanto a série a ser estudada é das Despesas da empresa – D01. Na Figura 9 pode-se observar o gráfico da série original das despesas (D01) e uma diferenciação (D(D01)).
Figura 9 – Gráfico da Série original das Despesas e Série diferenciada

Como ficou evidenciado na Figura 9 a série ficou estacionária após a aplicação de uma diferenciação. Nos gráficos referentes a FAC e FACP, pode-se notar que há respectivamente um lag indicando a parte q de médias móveis e um lag para a parte p de autocorrelação. Ou seja, há o indício de que o modelo ideal seja ARIMA(1,1,1).
Todavia o modelo que apresentou melhor desempenho em relação a série foi o ARIMA(1,1,0) a um nível de confiança de 95% (p<0,05).
O modelo apresentou ruído branco e do mesmo modo que a série R, não há aplicação do modelo ARCH, já que, foi feita a análise do correlograma quadrático dos resíduos a série D01 diferenciada. Na Figura 10 tem-se a previsão da série D01.
Figura 10 – Previsão do modelo ARIMA(1,1,0)

Essa previsão pode ser efetuada pela equação: ARIMA(1,1,0): ŷt = - 0,611491.yt-1 + εt ao nível de 5% de significância. As despesas da empresa para o próximo semestre estão descritas na Tabela 3.
Tabela 3 – Previsões de Despesas
Mês |
yt |
Previsão |
Abril/12 |
50 |
28973,60 |
Maio/12 |
51 |
30632,36 |
Junho/12 |
52 |
29528,85 |
Julho/12 |
53 |
30262,98 |
Agosto/12 |
54 |
29774,59 |
Setembro/12 |
55 |
30099,49 |
5 Conclusão
A empresa em estudo encontra-se no primeiro semestre estável, obtendo um lucro no segundo semestre, possivelmente em decorrência do volume de serviços realizados no mês de outubro, sendo identificado como evento externo a ocorrência do período eleitoral.
De acordo com os resultados obtidos pela analise estatística a empresa encontra-se no negativo alguns meses do ano e outros meses com um lucro baixo. Levando em consideração o risco em que a empresa esta exposta e a alta competitividade no meio gráfico a mesma deve observar detalhadamente o seu plano de negócios e suas atividades gerenciais, principalmente no setor financeiro.
Foi possível verificar que as séries R (Receitas) e D01 (Despesas) adequaram-se a modelos diferentes devido ao comportamento distinto das séries ao longo do tempo. A série R segue as características do modelo ARIMA(1,1,1), enquanto a série D01 o modelo ARIMA(1,1,0). Efetuadas as previsões dos modelos aceita-se a aplicação da equação do lucro, que é representada por Lucro = Receita – Custo. Na Tabela 3 estão descritas as previsões de lucro para o próximo semestre da empresa.
Tabela 4 – Previsões de Lucro
Mês |
Receita prevista |
Despesa Prevista |
Lucro previsto |
Abril/12 |
121420,0 |
28973,60 |
92446,4 |
Maio/12 |
92701,2 |
30632,36 |
62068,84 |
Junho/12 |
101870,1 |
29528,85 |
72341,25 |
Julho/12 |
98942,8 |
30262,98 |
68679,82 |
Agosto/12 |
99877,4 |
29774,59 |
70102,81 |
Setembro/12 |
99579,0 |
30099,49 |
69479,51 |
Após realizar a análise financeira da empresa e através do balanço financeiro, considerando o período de março de 2008 a fevereiro de 2012, recomenda-se para a empresa gráfica, buscar alternativas que viabilizem economicamente sua existência principalmente no primeiro semestre. Também se sugere que a empresa realize uma análise criteriosa de quais despesas possam ser reduzidas para obter maior lucratividade.
Existe uma infinidade de instrumentos que podem ser aplicados para facilitar a estruturação das contas e produção das empresas. Por isso, sugere-se que sejam desenvolvidos outros estudos nos processos internos da gráfica para torná-la mais eficaz e competitiva, ainda mais considerando que, com quatro anos de existência, a mesma pode ser avaliada nova no mercado.
Referências
BOX, G.E.; JENKINS, G.M.; REINSEL, G.C. Time series analysis: Forecasting and control. 3 ed. New Jersey: Printice Hall, 1994.
FERRAZA, D. C.; RAUBER, D. Fazenda Santo Antônio: um estudo de caso sobre fluxo de caixa. Revista TECAP – n. 02, Ano 02, v. 2, 2008.
FUJI, A.H. O conceito de lucro econômico no âmbito da contabilidade aplicada. Revista Contabilidade & Finanças - USP, São Paulo, n. 36, p. 74 - 86, 2004.
MACERAU, W. M. Modelos de série temporal para previsão de vendas de bebidas a base de soja da cocamar cooperativa agroindustrial. 2009 Maringá.
MORETTIN, Pedro A.; TOLOI Clélia M.. Métodos quantitativos: séries temporais. São Paulo: Atual, 1986.
MORETTIN, Pedro A.. Enconometria financeira: um curso de séries temporais financeiras. São Paulo: Blucher, 2008.
SILVA, C. A. T.; SANTOS, J. O.; OGAWA, J. S. Fluxo de Caixa e DOAR. Caderno de Estudos nº 9 – São Paulo – IPECAFI, 1993. Disponível em: http://www.eac.fea.usp.br/cadernos/completos/cad09/caixa_doar.pdf. Acesso em: 22 Jul. 2013.
SOUZA, Reinaldo Castro; CAMARGO, Maria Emilia. Análise e previsão de séries temporais: os modelos ARIMA. Ijuí: Sedigraf, 1996.
TELÓ, A. R. Desempenho organizacional: planejamento financeiro em empresas familiares. Revista FAE, Curitiba, v.4, n.1, p.17-26, 2001.