Introdução
As operações em mercados futuros têm figurado como uma importante alternativa para que investidores e produtores se protejam contra a volatilidade de preços inerente as atividades financeiras e produtivas. Neste sentido, o procedimento comumente utilizado por estes agentes baseia-se em estratégias de hedge, onde investidores assumem posições de compra ou venda de ativos no mercado futuro a fim de eliminar ou reduzir o risco dos investimentos.
Entre os principais beneficiários deste mecanismo de proteção estão os produtores de commodities agrícolas. O agronegócio brasileiro tem se destacado pela sua expressiva influência na economia do país, tendo a produção de soja como um de seus principais expoentes. O que segundo o Ministério da Agricultura, Pecuária e Abastecimento (MAPA, 2012), se reflete nas estimativas de que a produção brasileira da soja em grão atinja 88 milhões de toneladas em 2021/2022, uma projeção 17 milhões de toneladas maior em relação ao que o Brasil deve produzir na safra de 2011/2012.
A produção da soja, como das demais commodities agrícolas, não possui uma oferta ou demanda controlável, sendo sua oferta dependente das condições climáticas, das enfermidades durante o plantio e da qualidade logística de escoamento da safra e sua demanda da produção e do nível esperado de consumo no mercado externo. Dada à incerteza presente no mercado agrícola, tanto produtores como compradores buscam os mercados futuros como uma forma de se proteger contra a oscilação inesperada de preços. Os produtores procuram cobrir os custos ou ainda garantir uma margem de lucro que os permita dar continuidade a atividade produtiva. Os compradores, por sua vez, buscam fixar um preço de compra, o que propicia um conhecimento prévio das despesas e ganhos gerados pela comercialização.
Assim sendo, diversos estudos investigaram o emprego de estratégias em mercados futuros para o mercado brasileiro, entre os quais estão: Martins e Aguiar (2004), calculando a efetividade do hedge entre diversas regiões do Brasil e os contratos futuros de soja em grão da Chicago Board of Trade (CBOT); Santos, Botelho Filho e Rocha (2008), ao estimar a efetividade e a razão ótima de hedge para a região do Estado brasileiro de Goiás e os contratos futuros de soja na BM&F/Bovespa; Maia e Aguiar (2010), que avaliaram os retornos e os riscos de estratégias de hedge para as dez principais regiões produtoras de soja do Brasil em relação aos contratos futuros de soja da CBOT; e Souza, Martines Filho e Marques (2012), que analisaram a eficiência de estratégias de hedge simultâneo entre a soja produzia na região Centro-Oeste do Brasil e os contratos futuros de preço e taxa de câmbio da BM&F/Bovespa.
Nesse contexto, o presente trabalho teve como objetivo estimar dinamicamente a razão de hedge ótima para o mercado brasileiro de soja, por meio de um modelo DCC-GARCH (Dynamic Conditional Correlation-Generalized Autoregressive Conditional Heteroskedasticity). O procedimento tradicionalmente empregado para esta estimativa baseia-se na definição de um percentual de produção física que o produtor deve negociar em mercados futuros a fim de reduzir ou minimizar o risco de preços, sendo este percentual considerado como constante durante toda a operação. A estimação dinâmica, contudo, emprega a matriz de covariância condicional obtida pelo modelo DCC-GARCH para obter a razão de hedge ótima a cada momento do tempo, o que permite gerenciar as decisões de investimento de forma mais eficiente.
1 Materiais e métodos
Para realização deste estudo foram utilizados dados referentes às cotações spot diárias em dólares da Soja dos indicadores de preço do Centro de Estudos Avançados em Economia Aplicada da Escola Superior de Agricultura Luiz de Queiroz (CEPEA/ESALQ) e dos contratos futuros da CBOT, correspondentes ao período de 13/06/2006 à 18/06/2013. O período escolhido, por sua vez, deve-se a disponibilidade conjunta dos dados até o momento de coleta dos mesmos, perfazendo um total de 1768 observações diárias.
Assim, a amostra selecionada será empregada neste estudo de acordo com o marco teórico da lei do preço único, como descrito por Margarido e Fernandes (2001) e Corso, Silva e Duclós (2006). O modelo central desenvolvido pelos autores baseia-se na premissa de que variações nos preços externos de um dado bem se refletem em variações nos preços internos do mesmo. Desse modo, apoiando-se na chamada lei do preço único, segundo a qual produtos homogêneos devem custar valores semelhantes em mercados diferentes, quando expressos pela mesma moeda.
O estudo destes autores adota o pressuposto de que os preços domésticos da soja, cotado em dólares, é função do seu preço mundial. Analogamente, o presente estudo assumirá que o preço spot da soja brasileira, cotado em dólares, será uma função do seu preço mundial, representado pela cotação dos contratos futuros negociados na CBOT. O modelo que servirá como base teórica para este estudo é descrito como em Margarido e Fernandes (2001), sendo apresentado pela Equação [1].
Balke e Fomby (1997) enfatizam que o conceito de co-integração pressupõe que o ajustamento dos desvios do equilíbrio de longo prazo é feito instantaneamente a cada período, isto é, seguindo um padrão linear. No entanto, como destacado por Stigler (2010), os comportamentos diferenciados de diversas séries econômicas invalidam a hipótese de linearidade. Desse modo, visando auferir qual modelo melhor se ajusta aos dados, Hansen e Seo (2002), propuseram um teste que tem como hipótese nula a existência de cointegração linear e hipótese alternativa de cointegração com thresholds (regimes), também chamado de não linear.
O conceito de cointegração threshold foi introduzido por Balke e Fomby (1997), e discutido computacionalmente por Stigler (2010). De um modo geral, o modelo com regimes permite levar em consideração as principais criticas existentes contra a cointegração linear. Diferentemente dessa, o ajustamento não precisa ocorrer instantaneamente, e sim quando os desvios excederem um limite crítico. Assim, baseando seu processo de ajustamento no modelo self-exciting threshold auto-regressive (SETAR), o qual é discutido em Tong (1990) e Stigler (2010). No modelo SETAR, os coeficientes autorregressivos tomam diferentes valores, dependendo se o valor prévio está acima ou abaixo de certo limiar, exibindo regime de alterações dinâmicas, o que permite considerar de forma mais realista variações excessivas no nível de preços dos ativos.
Stigler (2010) enfatiza que enquanto o trabalho de Balke e Fomby (1997) centrou-se na representação da relação de longo prazo, a extensão para um modelo threshold vector error correction model (TVECM) foi feita por vários autores, sendo o limiar de regimes aplicado no termo de correção de erro (Granger e Lee, 1989; Seo, 2006) ou nas defasagens e intercepto (Hansen e Seo, 2002; Lo e Zivot, 2001). Tal conceito recebeu um interesse significativo devido ao teorema conhecido como representação de Granger, que afirma que as variáveis cointegradas possuem um modelo vetorial de correção de erro (VECM), que pode ser visto como um modelo VAR (vector autoregressive model), incluindo uma variável que representa os desvios do equilíbrio de longo prazo. Esse modelo visa efetuar ajustes em curto prazo para corrigir os desvios ocorridos no equilibrio de longo prazo. Após rejeitar a hipótese de cointegração linear através do teste de Hansen e Seo (2002), foi estimado um modelo TVEC, seguindo a descrição de Stigler (2010), e representado pelas Equações [2], [3] e [4].
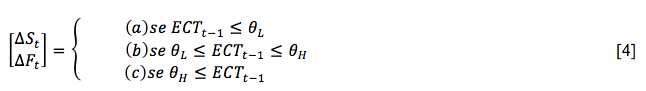
2 Resultados e discussão
Inicialmente, com o intuito de evidenciar a evolução das séries estudadas é apresentado o Gráfico 1. Conforme Daniel et al. (2011), depois de uma alta no preço de alguns alimentos, entre 2004 e 2008, houve neste ultimo ano um declínio acentuado, decorrente da crise mundial, com o preço dos alimentos voltando a se recuperar no inicio de 2009. Este comportamento também pode ser observado nas cotações spot e futuro da soja, as quais apresentam uma evolução similar ao longo de todo o período estudado.
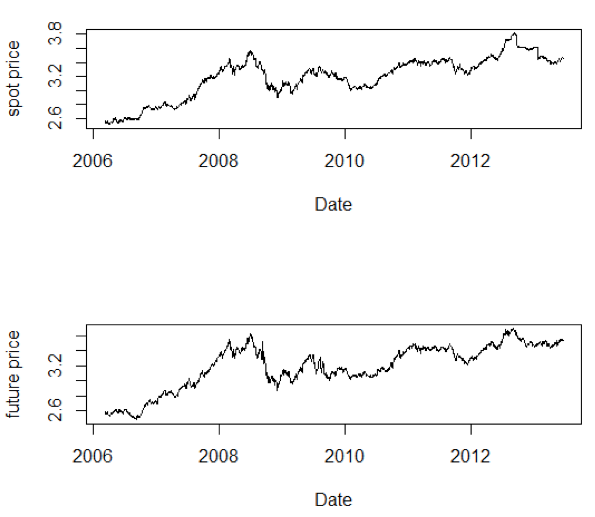Gráfico 1. Cotações diárias do logaritmo do preço spot
e futuro soja no período de 13/06/2006 à 18/06/2013
No que diz respeito a análise de séries temporais, a estacionariedade é uma condição necessária. No entanto, séries não-estacionarias podem se mostrar bastante uteis para a identificação de equilíbrios de longo prazo entre variáveis. A fim de avaliar se as variáveis utilizadas apresentam esta característica foi realizado o teste ADF, onde a hipótese nula é de que a série possui raiz unitária (não-estacionária), contra a alternativa de estacionariedade da mesma. Os resultados do teste ADF são apresentados na Tabela 1.
Tabela 1 - Valores calculados dos testes ADF para soja em nível, primeira diferença e resíduo do relacionamento do longo prazo.
Variável |
Estatística |
p-valor |
Estatística |
p-valor |
Soja spot (nível) |
-1,783 |
0,389 |
-2,372 |
0,394 |
Soja futuro (nível) |
-1,674 |
0,444 |
-2,341 |
0,410 |
Soja spot (diferença) |
-24,967 |
<0,001 |
-24,969 |
<0,001 |
Soja futuro (diferença) |
-20,444 |
<0,001 |
-20,441 |
<0,001 |
Resíduo |
-3,729 |
0,003 |
-3,723 |
0,020 |
A Tabela 1 apresenta os resultados do teste ADF aplicado para os preços spot e futuro da soja em nível e primeira diferença, além do resíduo do modelo de longo prazo. Como resultado, o teste ADF identificou presença de raiz unitária nos preços dos mercados spot e futuro, no entanto, quando submetidas ao procedimento de diferenciação as variáveis se tornaram estacionarias. Quando aplicado aos resíduos do modelo de longo prazo, o teste, tanto com constante ou com constante e tendência, rejeitou sua hipótese nula, indicando a estacionariedade do resíduo. Assim sendo, é plausível afirmar que existe uma relação de equilíbrio de longo prazo entre os preços spot e futuro da soja, com tal resultado tornando viável a utilização de estratégias de hedge para esse mercado.
Assim, pretende-se dividir as séries de preços em diferentes regimes a partir de um modelo TVEC, a fim de permitir um melhor ajustamento das alterações dinâmicas presentes nas variáveis. Esta modelagem permite considerar de forma mais realista os eventos econômicos que afetam o nível de preços dos ativos, propiciando uma análise mais consistente. Como primeiro passo, a fim de viabilizar o emprego do modelo TVEC, foi aplicado o teste de Hansen e Seo (2002), o qual testa a hipótese nula de cointegração linear versus cointegração com regimes. Os resultados do teste de Hansen e Seo (2002) podem ser vistos na Tabela 2. Como resultado, constatou-se que a hipótese nula de cointegração linear foi rejeitada, indicando que o modelo com regimes possui uma melhor adequação aos dados.
Depois de constatada a viabilidade do emprego do modelo não-linear, a escolha das defasagens utilizadas, bem como o número de regimes, se deu com base no critério AIC. Os resultados obtidos na estimação do modelo TVEC são apresentados na Tabela 2.
Tabela 2 - Modelo TVEC estimado para as relações entre os preços spot e futuro da soja
Regime de Baixa (5,2%) |
Regime de Média (78%) |
Regime de Alta (16,8%) |
||||
Coeficiente |
Spot |
Futuro |
Spot |
Futuro |
Spot |
Futuro |
ECT |
0,074 |
0,564 |
-0,035 |
-0,006 |
-0,059 |
0,005 |
Constante |
0,011 |
0,056 |
<0,001 |
<0,001 |
0,006 |
0,002 |
Spot_1 |
0,038 |
0,601 |
-0,140 |
0,055 |
0,072 |
-0,087 |
Futuro _1 |
0,065 |
-0,581 |
0,232 |
0,013 |
0,045 |
0,116 |
Spot_2 |
-0,205 |
-0,223 |
-0,103 |
-0,004 |
0,147 |
0,172 |
Futuro_2 |
-0,080 |
-0,220 |
0,100 |
-0,041 |
0,026 |
0,008 |
Hansen e Seo (2002) Estatística p-valor 42,691 <0,001 |
||||||
Com base nos resultados apresentados na Tabela 2, percebe-se a predominância de dados pertencentes ao regime de estabilidade (78%), seguido pelo de alta (16,8%) e baixa (5,2%). Tais resultados podem ser entendidos da seguinte forma: i) o regime de baixa, com menor representatividade, indica os momentos de baixa variação nos preços, onde ocorre transmissão dos preços spot para o futuro, o que pode estar relacionado, sobretudo, aos custos de transação da base; ii) o regime de estabilidade nas variações, predominante ao longo da amostra, indica a presença de variações não tão intensas como em regimes de alta, onde ocorre transmissão de preços do futuro para o spot, com tal transmissão sendo denotada pela tentativa desse mercado se reger pela lei do preço único, uma vez que na maior parte da amostra o mercado internacional consegue transmitir seus preços para o mercado interno, e por fim; iii) o regime de altas variações, que representa momentos de grandes variações nos preços, tais como crises financeiras, em que a volatilidade do mercado é alta e a liquidez é baixa. Contudo, nesse regime não há transmissões de preço estatisticamente significativas, o que implica que choques maiores que o threshold não são eliminados ao longo do tempo, reduzindo a eficácia da estratégia de hedge.
A fim de validar o modelo acima, buscou-se identificar a presença de correlação serial nos resíduos e resíduos ao quadrado, por meio do teste Q de Ljung e Box (1978). Nenhuma defasagem testada (1 a 5) obteve valor significativo para o teste Q dos resíduos do modelo, no entanto, quando considerado suas formas quadráticas todas as defasagens se mostraram estatisticamente significativas. Esse resultado confirma a presença do efeito heteroscedástico condicional, sugerindo que a volatilidade dos resíduos pode ser modelada. Desse modo, utilizando os resíduos obtidos através do modelo TVEC foi estimada a matriz de covariância condicional com um modelo DCC-GARCH. A formulação matemática do modelo foi representada pela Equação [5] e os resultados são apresentados na Tabela 3.
Gráfico 2. Volatilidades dos mercados spot e futuro, sua correlação e razão de hedge ótima obtidos com o modelo DCC-GARCH
No que diz respeito a evolução da correlação dinâmica estimada entre os mercados spot e futuro, o Gráfico 2 ilustra um comportamento estável ao longo do tempo, com exceção primeiros meses de 2013, onde se constatou uma maior volatilidade no mercado interno brasileiro, acompanhada por uma redução na correlação com o mercado internacional. Além disso, na maior parte do período analisado as correlações ficam entre o intervalo de 0,3 a 0,7, indicando uma forte e relevante oscilação entre os mercados.
As estimativas tradicionais de hedge consistem em definir uma alocação constante de um dado recurso no mercado futuro a fim de minimizar os riscos inerentes às oscilações de preços do ativo. Desse modo, o agente financeiro aloca uma porcentagem de seus recursos em operações de hedge, mantendo-a constante durante toda a operação. No entanto, como demonstrado pelo Gráfico 2, essa alocação ótima de recursos não é constante ao longo do tempo, apresentando grande variabilidade. A razão ótima de hedge dinâmica calculada para a amostra empregada neste estudo variou entre 5% e 90%, indicando que a estratégia de alocar uma porcentagem constante de recursos durante toda a operação pode se apresentar bastante falha, uma vez que a razão ótima de hedge apresenta grandes variações ao longo do tempo.
Por fim, a partir da razão ótima de hedge, foi calculada a efetividade das operações entre os mercados spot e futuro da soja, onde foi obtido o valor de 29,04%. Neste sentido, tal resultado sugere que 29,04% do risco de oscilação nos preços pode ser reduzido através de operações de hedge com contratos futuros da CBOT.
3. Conclusão
O presente trabalho teve como objetivo estimar dinamicamente a razão de hedge ótima entre o mercado brasileiro de soja e os contratos futuros da CBOT, por meio de um modelo DCC-GARCH. De um modo geral, os resultados permitiram concluir que estratégias tradicionais de hedge podem se apresentar inconsistentes, uma vez que a influência de custos de transação e grande variabilidade ao longo do tempo na razão ótima entre os mercados não são identificados por elas. De modo que ao se considerar a abordagem dinâmica é possível obter uma maior gama de informações, tais como clusters de volatilidade e uma correlação dinâmica entre as variáveis, a fim auxiliar na redução do risco e na alocação de recursos de forma mais eficiente.
Por fim, destacam-se como sugestões para estudos futuros a estimação de hedge dinâmico em diferentes commodities e seus respectivos mercados futuros, além de estudos que consideram diferentes mercados internacionais.
Referências
BALKE, NATHAN S.; FOMBY, THOMAS B. Threshold Cointegration. Philadelphia: International Economic Review, v. 38, n. 3, p. 627-645, 1997.
CORSO, JANSEN MAIA; SILVA, WESLEY VIEIRA; DUCLÓS, LUIZ CARLOS. Avaliação do processo de transmissão dos preços da soja praticados nos mercados físico brasileiro e norte-americano. Blumenau: Revista de Negócios, v. 11, n. 3, 2006.
DANIEL, LINDOMAR PEGORINI; OLIVEIRA, ADEMIR MACHADO.; PREMOLI, MARCUS VINÍCIUS ZANDONADI; REZENDE, ADRIANO ALVES. Análise da recente alta internacional dos preços das commodities alimentares Previsão e mudança estrutural. Brasília: Revista de Política Agrícola, v.20, n. 4, p.7-20, 2011.
ENGLE, ROBERT. F. Dynamic conditional correlation: A simple class of multivariate generalized autoregressive conditional heteroskedasticity models. Washington: Journal of Business and Economic Statistics, v.20, n.3, p. 339-350, 2002.
ENGLE, R. F.; GRANGER, CLIVE W. J. Cointegration and error correction: representation, estimation and testing. Chicago: Econometrica, v. 55, n. 2, p. 251-276, 1987.
GRANGER, CLIVE W. J.; LEE, T. H. Investigation of Production, Sales and Inventory Relationships Using Multicointegration and NonSymmetric Error Correction Models. New York: Journal of Applied Econometrics, v. 4, p. 145-159, 1989.
HANSEN, BRUCE E.; SEO, BYEONGSEON. Testing for two-regime threshold cointegration in vector error-correction models. Amsterdam: Journal of Econometrics, v. 110, n.2, p. 293-318, 2002.
LJUNG, GRETA. M.; BOX, GEORGE E. P. On a measure of lack of fit in time series models. Cambridge: Biometrika, v. 65, n.2, p. 297–303, 1978.
LO, MING CHIEN; ZIVOT, ERIC. Threshold cointegration and nonlinear adjustment to the law of one price. New York: Macroeconomic Dynamics, v. 5, n. 4, p. 533-576, 2001.
MAIA, FÁBIO NEVES DE CARVALHO DA SILVA; AGUIAR, DANILO ROLIM DIAS. Estratégias de hedge com os contratos futuros de soja da Chicago Board of Trade. São Carlos: Gestão & Produção, v.17, n.3, p. 617-626, 2010.
MARGARIDO, MÁRIO A.; FERNANDES, JOCELINNE MARIE. Análise da formação de preços no mercado internacional de soja: o caso do Brasil. São Paulo: PUCSP, 2001. (Textos para Discussão. Programa de Estudos Pós-Graduados em Economia Política).
MARTINS, ANAMARIA GAUDENCIO; AGUIAR, DANILO ROLIM DIAS. Efetividade do hedge de soja em grão brasileira com contratos futuros de diferentes vencimentos na Chicago Board of Trade. Viçosa: Revista de Economia e Agronegócio, v.2, n. 4, p. 449-472, 2004.
MAPA (2012). Ministério da Agricultura Pecuária e Abastecimento - Assessoria de Gestão Estratégica. Brasília: Brasil Projeções do Agronegócio 2011/2012 a 2021/2022.
RIGHI, MARCELO BRUTTI; CERETTA, PAULO SERGIO. Global Risk Evolution and Diversification: a Copula-DCC-GARCH Model Approach. Rio de Janeiro: Brazilian Finance Review, v. 10, n.4, p. 529-550, 2012.
SANTOS, MARCELO PEREIRA; BOTELHO FILHO, FLÁVIO BORGES; ROCHA, CARLOS HENRIQUE. Hedge de mínima variância na BM&F para soja em grãos no Centro-Oeste. Brasília: Sociedade e Desenvolvimento Rural, v. 2, n. 1, p.203-212, 2008.
SEO, MYUNGHWAN. Bootstrap testing for the null of no cointegration in a threshold vector error correction model. Amsterdam: Journal of Econometrics, v.127, n. 1, p. 129-150, 2006.
SOUZA, WALDEMAR ANTONIO DA ROCHA; MARTINES FILHO, JOÃO GOMES; MARQUES, PEDRO VALENTIM. Análise de estratégias de hedge simultâneo para a produção de soja no Centro-Oeste. Curitiba: Revista de Economia, v. 38, n. 2, 2012.
STIGLER, MATTHIEU. Threshold cointegration: overview and implementation in R. Working Paper, 2010.
TONG, HOWELL. Non-Linear Time Series: A Dynamical System Approach. Oxford: Oxford Science Publications, 1990. 564 p.