1. Introdução
A variabilidade, segundo Montgomery (2009), é sinônimo de desperdício de dinheiro, tempo e esforços. Para isso, diversas ferramentas de estratégia foram criadas em busca de estabelecer um controle de qualidade de processo. Montgomery (2009) ressalta que, o controle estatístico do processo é uma ferramenta bastante eficaz na resolução de problemas, útil na obtenção da estabilidade do processo e aumento da capacidade através da redução de variabilidade.
O Controle Estatístico do Processo (CEP) pode ser descrito como uma ferramenta de monitoramento on-line da qualidade. Através da inspeção por amostragem, operando ao longo do processo, com o objetivo de verificar a presença de causas especiais, ou seja, causas que não são naturais ao processo e que podem prejudicar a qualidade do produto manufaturado. Uma vez identificadas as causas especiais, podemos atuar sobre elas, melhorando continuamente os processos de produção e, por conseguinte, a qualidade do produto final.
Neste trabalho, investiga-se a aplicação de mapeamento de controle estatístico de processos em uma indústria que fabrica peças técnicas em precisão, especializada em cortes e gravações em peças metálicas utilizando o processo de estampagem mecânica e química para o meio industrial tendo como matéria-prima principal o aço inoxidável. Diante disso, este estudo tem como objetivo analisar dois processos de produção de peças de precisão por estampagem mecânica e química. Um dos processos analisados trata-se da fabricação de etiquetas para botoeira de elevadores. Já o outro processo trata-se da fabricação de peças de precisão.
Os dois processos são de grande importância já que o não cumprimento das especificações pode gerar refugo e retrabalho, ocasionando custos de produção para a empresa. O trabalho está estruturado em cinco seções. Além desta introdução, a segunda seção apresenta o referencial teórico, já a terceira seção apresenta os procedimentos metodológicos com as definições dos processos e as etapas necessárias para execução do estudo, a seção 4 trata da análise dos resultados e na seção 5 são apresentadas as principais conclusões do presente estudo.
2. Controle Estatístico de Processo
Toda empresa precisa de técnicas que permitam ao seu produto a qualidade desejada. Não é possível colocar a responsabilidade apenas sobre as pessoas, exigindo que elas façam o melhor que podem ou cobrando resultados, é necessário o uso de ferramentas que auxiliem no controle de falhas e no aperfeiçoamento dos processos de produção (CORTIVO, 2005). Neste contexto, o Controle Estatístico de Processo (CEP) representa uma ferramenta da qualidade que possibilita monitorar as características de relevantes de um processo, assegurando sua manutenção dentro de limites preestabelecidos e indicando quando adotar ações de correção e melhoria. O uso desta ferramenta pode trazer grandes benefícios para a empresa, como a satisfação de seus clientes e menor custo de produção (MIYATA et al., 2010). Saldanha et al. (2013) conduziram um estudo estatístico ao aplicar diversas ferramentas estatísticas no processo de fabricação em uma empresa do segmento químico do Rio Grande do Sul.
Os gráficos de controle consistem em uma importante ferramenta do CEP, segundo Montgomery (2009) os gráficos de controle podem ser classificados em dois tipos gerais: os gráficos de controle para variáveis e os gráficos de controle para atributos.
Os atributos são características que quando comparadas com um certo padrão (especificações), podem assumir apenas valores discretos, ou seja, classificação como conforme ou não-conforme, ou contagem de defeitos (RIBEIRO; CATEN, 2013). De acordo com Montgomery (2009) os gráficos de atributos são de grande utilidade nas indústrias de serviços e na busca pela melhoria da qualidade não-industrial, pois muitas das características de qualidade que existem nesses ambientes são de difícil mensuração em uma escala numérica. A Tabela 1 a seguir apresenta os quatro tipos de carta de atributos.
Tabela 1 – Tipos de carta de controle por atributos
Tipo de carta |
Aplicabilidade |
Carta p |
Mede a fração de produtos defeituosos ou produtos não-conformes em uma amostra (as amostras podem ser de tamanhos diferentes) |
Carta Np |
Monitora o número de unidades não conformes (as amostras deve ter do mesmo tamanho) |
Carta c |
Monitora o número de não-conformidades (defeitos) verificados em um grupo (as amostras devem ter o mesmo tamanho) |
Carta u |
Monitora o número de não-conformidades por unidade produzida, o número de não conformidades é expresso em relação a cada unidade (as amostras podem ter tamanhos diferentes). |
Fonte: Ribeiro e Caten (2013).
2.1. A Função Perda de Taguchi
A abordagem tradicional de qualidade está fortemente ligada com a ideia de atender às especificações. Nesse enfoque, se um produto atende as especificações ele possui boa qualidade, caso contrário, ele é um produto defeituoso. Mas para Taguchi a qualidade, ou a falta de qualidade, pode ser avaliada através da perda imposta por um produto ou por atingir o alvo com a menor variabilidade possível (RIBEIRO; CATEN, 2013).
Ainda segundo os autores a abordagem proposta por Taguchi consiste em usar a função perda para avaliar o processo. A Figura 1 apresenta o comparativo entre a abordagem tradicional para a estimativa de perda e a abordagem de Taguchi, a linha vermelha representa a abordagem tradicional, já a linha azul representa a abordagem de Taguchi.
Figura 1 – Abordagem tradicional e abordagem Taguchi. Fonte:Ribeiro e Caten (2013).

Li = k (yi – m)² (1)
A perda financeira associada ao desvio da meta é expressa por Li, já o valor medido para a característica da qualidade em estudo é expresso por yi, a meta para a característica de qualidade é representada por m e o coeficiente k de perda da qualidade, que converte o desvio do alvo em R$ é dado por Ao/ ∆², onde Ao é o custo de reparo ou substituição do produto e ∆² é o desvio da meta que exigiria reparo ou substituição (RIBEIRO; CATEN, 2013).
3. Procedimentos metodológicos
O presente estudo foi realizado de acordo com quatro etapas: definições do indicador, tipo e especificações; seguido da definição do tipo de carta; definição do tamanho da amostra e frequência de amostragem, e por fim definição da função perda. O primeiro processo analisado consiste na fabricação de etiquetas para botoeiras de elevadores por estampagem mecânica em lotes de 200 unidades, o material utilizado consiste no aço inox que é gravado em alto relevo ou policarbonato texturizado em impressão serigráfica. Neste caso, as interferências ao processo estão ligadas a erros de operação da máquina de corte. As etiquetas tem tamanho padrão de 32 x32 mm. A Figura 2 apresenta as etiquetas.
Figura 2 – Etiquetas para botoeiras de elevadores. Fonte: autores (2014).

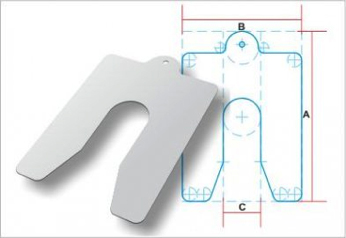
O segundo processo consiste na fabricação de peças de precisão porfotocorrosão (Estampagem Química de precisão) mantendo assim mais resistência à fadiga, consegue-se dobras do metal sem o auxílio mecânico e sem custo de ferramental, as interferências desse processo estão relacionadas a máquina. As peças são produzidas em lotes pequenos de até 5 unidades. A Figura 3 apresenta calços calibrados em aço inox (80mmx70mmx0,20mm) fabricados pelo processo de fotocorrosão.
Figura 3 – Peça de precisão. Fonte: autores (2014).
Para identificar as peças para retrabalho ou refugadas do primeiro processo analisado, é feita uma inspeção pelo operador, no qual o mesmo marca as peças defeituosas e retira do lote que vai ser enviado para o cliente. No segundo processo a inspeção de não conformidades (manchas, risco, rebarbas) também é realizada pelo operador que identifica se o número de não conformidades está dentro do tolerado. Os dois processos analisados apresentam indicador do tipo menor é melhor. De acordo com Ribeiro e Caten (2013) as características do tipo menor é melhor tendem a apresentar uma distribuição de probabilidade assimétrica à direita, pois muitas vezes existem limitações tecnológicas dificultando a obtenção de valores baixos. Enquanto que, muitos casos de variabilidade podem gerar valores altos, assim apresentam apenas limite superior de especificação.
No processo de fabricação das etiquetas para botoeiras de elevador do lote de 200 unidades a meta de retrabalho ou refugo consiste em 12 unidades. Já no processo de fabricação de peças de precisão o número de não conformidades por unidade tolerado é três. O tipo de carta utilizado neste estudo foi a carta para atributos, onde no primeiro processo utilizou-se a carta p. Buscou-se medir a fração de produtos defeituosos em uma amostra de tamanho considerável e constante (200 unidades). De acordo com Ribeiro e Caten (2013) as cartas para atributos exigem subgrupos de tamanho considerável, em geral de 50 a 200 unidades ou mais, para serem eficientes na detecção de alterações no processo. Para cada subgrupo anotou-se os valores de:
n= número de itens inspecionados
d= número de defeitos (não conformidades)
k= número de subgrupos
A fração média de não conformidades foi calculada pela equação (2) a seguir.
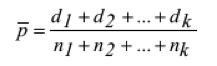 (2)
(2)
O desvio - padrão foi calculado utilizando a equação (3), como as amostras coletadas tiveram tamanhos iguais, utilizou-se a média dos tamanhos das amostras.
![]() (3)
(3)
Os limites de controle superior e inferior foram calculados usando a equação (4) e (5), respectivamente.
![]() (4)
(4)
![]() (5)
(5)
No segundo processo analisado utilizou-se a carta u, pois buscou-se monitorar o número de não conformidades por unidade produzida, onde a amostra analisada continha 5 unidades. Inicialmente calculou-se o número médio de não conformidades por unidade utilizando a equação (6) e em seguida calculou-se o desvio padrão pela equação (7).
 (6)
(6)
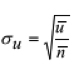 (7)
(7)
Onde: c é o número de não conformidades na amostra i; n é o tamanho da amostra e k é o número de subgrupos. Em seguida foram calculados os limites de controle superior e inferior para o número de não conformidades por unidade utilizando a equação (8) e (9).
![]() (8)
(8)
![]() (9)
(9)
4. Resultados
Primeiramente foi feita uma reunião dentro do processo produtivo da fábrica envolvendo a gerência e os operadores, onde foi definida a equipe responsável, os horários de coleta e o tamanho da amostra. No processo de fabricação de etiquetas para botoeiras de elevador o tamanho de amostra coletado para o estudo da fração de produtos defeituosos por lote de 200 unidades foi de 30 turnos coletados durante 15 dias, coletou-se amostras do turno da manhã e do turno da tarde conforme Tabela 2 a seguir.
Tabela 2: Coleta de dados
Dia |
Turno |
lote |
Di |
P |
1 |
manhã |
200 |
22 |
0,1100 |
tarde |
200 |
25 |
0,1250 |
|
2 |
manhã |
200 |
17 |
0,0850 |
tarde |
200 |
18 |
0,0900 |
|
3 |
manhã |
200 |
37 |
0,1850 |
tarde |
200 |
29 |
0,1450 |
|
4 |
manhã |
200 |
21 |
0,1050 |
tarde |
200 |
17 |
0,0850 |
|
5 |
manhã |
200 |
20 |
0,1000 |
tarde |
200 |
25 |
0,1250 |
|
6 |
manhã |
200 |
8 |
0,0400 |
manhã |
200 |
24 |
0,1200 |
|
7 |
tarde |
200 |
29 |
0,1450 |
manhã |
200 |
18 |
0,0900 |
|
8 |
tarde |
200 |
22 |
0,1100 |
manhã |
200 |
30 |
0,1500 |
|
9 |
tarde |
200 |
33 |
0,1650 |
manhã |
200 |
21 |
0,1050 |
|
10 |
tarde |
200 |
16 |
0,0800 |
manhã |
200 |
17 |
0,0850 |
|
11 |
tarde |
200 |
20 |
0,1000 |
manhã |
200 |
29 |
0,1450 |
|
12 |
manhã |
200 |
23 |
0,1150 |
tarde |
200 |
25 |
0,1250 |
|
13 |
manhã |
200 |
19 |
0,0950 |
tarde |
200 |
22 |
0,1100 |
|
14 |
manhã |
200 |
22 |
0,1100 |
tarde |
200 |
17 |
0,0850 |
|
15 |
manhã |
200 |
25 |
0,1250 |
tarde |
200 |
20 |
0,1000 |
|
soma |
6000 |
671 |
0,1118 |
|
pmédio |
0,11183 |
|||
desvio p |
0,02229 |
|||
k |
30,00 |
|||
n |
200,00 |
|||
np |
22,4 |
Os dados foram coletados pelo operador de cada turno, responsável pela operação da máquina de estampagem mecânica no primeiro horário da manhã bem como no primeiro da tarde que o funcionário começava a operar a máquina, a coleta durou duas semanas e 1 dia, sendo que o primeiro dia de coleta iniciou em uma segunda – feira.
Para o processo de fabricação de peças de precisão foi analisada 30 amostras em subgrupos de 5 unidades no mês de maio, onde foram coletadas uma amostra por dia, conforme Tabela 3.
Tabela 3: Coleta de dados
Dia |
Tamanho da amostra |
nº de não-conformidades |
média de não-conformidades |
1 |
5 |
10 |
2 |
2 |
5 |
12 |
2,4 |
3 |
5 |
8 |
1,6 |
4 |
5 |
14 |
2,8 |
5 |
5 |
10 |
2 |
6 |
5 |
16 |
3,2 |
7 |
5 |
11 |
2,2 |
8 |
5 |
7 |
1,4 |
9 |
5 |
10 |
2 |
10 |
5 |
15 |
3 |
11 |
5 |
9 |
1,8 |
12 |
5 |
5 |
1 |
13 |
5 |
7 |
1,4 |
14 |
5 |
11 |
2,2 |
15 |
5 |
12 |
2,4 |
16 |
5 |
6 |
1,2 |
17 |
5 |
8 |
1,6 |
18 |
5 |
10 |
2 |
19 |
5 |
7 |
1,4 |
20 |
5 |
13 |
2,6 |
21 |
5 |
10 |
2 |
22 |
5 |
8 |
1,6 |
23 |
5 |
6 |
1,2 |
24 |
5 |
9 |
1,8 |
25 |
5 |
14 |
2,8 |
26 |
5 |
7 |
1,4 |
27 |
5 |
13 |
2,6 |
28 |
5 |
7 |
1,4 |
29 |
5 |
9 |
1,8 |
30 |
5 |
11 |
2,2 |
Soma |
150 |
295 |
|
u médio |
1,97 |
||
n médio |
5,00 |
||
Desvio |
0,63 |
Os dados foram coletados pelo operador responsável pela operação dos controles da máquina de fotocorrosão. Conforme Ribeiro e Caten (2013) a equação (10) representam a perda para processos do tipo menor é melhor.
![]() (10)
(10)
Onde y representa a média dos valores medidos, s o desvio padrão da amostra e k o coeficiente de perda.
Para o processo 1 de estampagem mecânica, é estimado que a fração de 0,12% de peças defeituosas por lote de 200 unidades produzidas, implica em uma perda monetária de R$24,00, logo ∆ = 0,12 e Ao =24,00. Já para o processo 2 de fotocorrosão, é estimado que a perda de 1 peça produzida implica em uma perda monetária de R$ 85,00,logo, ∆ = 1 e Ao = 85,00.
De acordo com Ribeiro e Caten (2013) a equação (11) revela a natureza dos problemas de qualidade. Assim se Q for maior que 1, a perda devido ao desvio da meta é preponderante e, provavelmente, será possível efetuar uma melhoria significativa no processo com facilidade. Já se Q for próximo de zero, o processo já está centrado e os problemas de qualidade são basicamente devidos à dispersão. Esse caso é mais difícil de resolver e, em geral, irá exigir ação sobre as causas comuns, ou seja ação sobre o sistema.
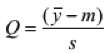 (11)
(11)
5. Análise e discussão dos resultados
Os resultados apresentados para os dois processos foram divididos em: estudo de estabilidade, estudos de capacidade e função perda.
5.1. Estabilidade do processo de estampagem mecânica
Através dos dados coletados do processo de estampagem mecânica, realizaram-se os cálculos de limites de controle no software excell para a carta p utilizando as equações (4) e (5) onde se obteve um limite de controle inferior (LCI) e um limite de controle superior (LCS) de, respectivamente, 0,04498 e 0,17869. A Figura 4 apresenta a carta prévia para fração de etiquetas não conformes na amostra. Observou-se que os turnos 5 e 11 foram considerados como causas especiais, pois esses pontos ficaram fora dos limites de controle, logo o processo não teve um comportamento estável.
Figura 4 – Carta prévia da fração de produtos não conformes do processo 1. Fonte: autores (2013).
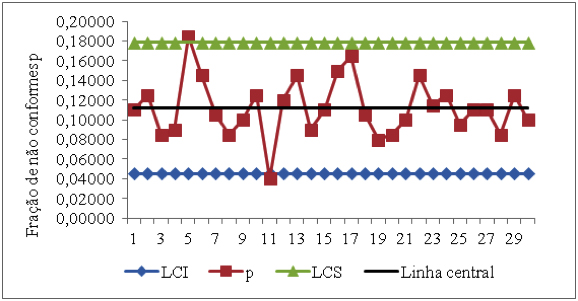
Com a identificação dos pontos relacionados a causas especiais, os mesmos foram eliminados e recalcularam-se os limites de controle. O novo cálculo dos limites foi feito no software ProCEP. A Figura 5 apresenta a carta de controle com os limites recalculados.
Figura 5 – Carta da fração de produtos não conformes do processo 1. Fonte: autores (2013).
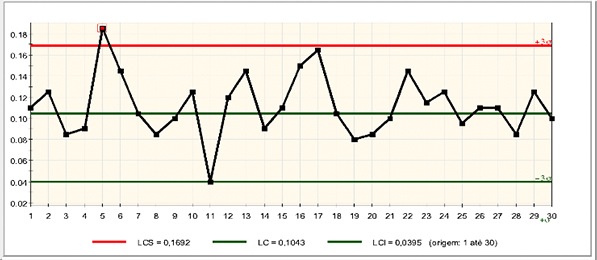
Pode-se verificar através da Figura 5, que o processo ainda não é estável e previsível ao longo do tempo, pois existe um ponto fora do limite de controle superior. Assim, as causas especiais do processo devem ser investigadas, analisadas e corrigidas. No dado coletado no turno 5, extraído do terceiro dia de coleta ocorreu erro de operação da máquina pelo operador, o que explica a causa especial apresentada. Quanto aos demais pontos fora da linha central, a variação se explica devido à troca de operador por turno.
5.2. Estabilidade do processo de fotocorrosão
A partir dos dados coletados do processo de fotocorrosão, realizaram-se os cálculos de limites de controle utilizando a equação (8) e (9) para a carta u. Obteve-se LCS e LCI igual a 3,8482 e 0,0852, respectivamente. A Figura 6 apresenta, a cartas u para o processo de fotocorrosão para peças de precisão onde utilizou-se o software Excel e a Figura 7 apresenta a mesma carta u, porem utilizando o software ProCEP.
Figura 6 – Carta de controle u para processo 2 no software Excell. Fonte: autores (2013).

-----
Figura 7 – Carta de controle u para o processo 2 no software ProCEP. Fonte: autores (2013).
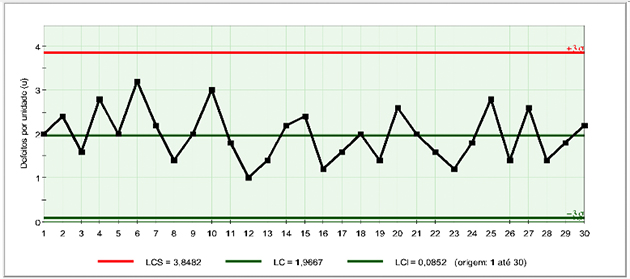
A partir da Figura 7 pode-se observar que o processo 2 não apresentou causas especiais, assim, o comportamento do processo é estável. Os motivos para ter se comportado de forma estável, pode ser devido ao processo de fotocorreção ser automatizado, onde o funcionário não realiza operações mecânicas passíveis de variabilidade pela interferência do homem.
5.3 Capacidade do processo de estampagem mecânica
Capacidade de um processo pode ser definida como "a capacidade do processo de produzir peças idênticas", por um longo período de tempo sob um determinado conjunto de condições. Objetivando demonstrar se um processo de fabricação específico é ou não viável. É a partir desta avaliação rigorosa que um fabricante pode analisar todas as características do produto e então, decidir se quer continuar com a produção, alterar especificações ou cancelar o projeto. Neste contexto, segundo Ribeiro e Caten (2013) a capacidade do processo em geral é expressa como o percentual de produtos conformes que o processo produz, que pode ser expresso pela equação (12):
![]() (12)
(12)
Assim para o processo estudado onde o p médio, ou seja, a fração de produtos fora do especificado é 0,104, e a capacidade do processo de produzir produtos conformes foi 90%:
Capacidade = (1- 0,014) x 100 = 90%
O processo de estampagem mecânica é do tipo menor é melhor, e em processos desse tipo o valor do LCI é teoricamente zero e, por esta razão, utiliza-se a especificação superior para avaliação de capacidade. A especificação superior para o processo de estampagem mecânica (meta gerencial) consiste em 12% de peças não conformes. De acordo com Ribeiro e Caten (2013) o percentual de não-conformes pode ser comparado com as expectativas e metas gerenciais, gerando um índice de capacidade Cp, dado pela equação (13).
 (13)
(13)
O resultado do calculo do Cp utilizando a equação (13) foi de 1,1505, logo, Cp > 1 o que significa que o processo de estampagem mecânica é potencialmente capaz. A Figura 8 apresenta a distribuição de probabilidade para o processo de estampagem mecânica, onde identificou-se que a probabilidade de uma amostra apresentar uma fração de não conformes inferior ao especificado é igual a 76,6205% e superior ao especificado consiste em 23,3795%. A Figura 9 apresenta a carta de capacidade do processo 1.
Figura 8 – Distribuição de probabilidade para o processo 1. Fonte: autores (2013).
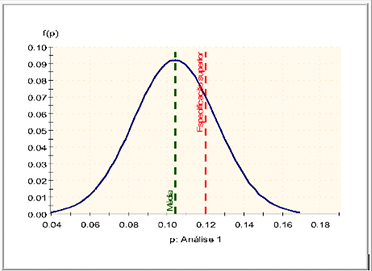
-----
Figura 9 – Carta de Capacidade do processo 1. Fonte: autores (2013).
5.4. Estudo de capacidade do processo de fotocorrosão
O processo de fotocorrosão, assim, como o processo de estampagem química é do tipo menor é melhor. Para o processo estudado onde o u médio, ou seja, o número de não conformidades por unidade é 1,9667 e a especificação superior para este processo (meta gerencial) consiste em 3 não conformidades por unidade produzida. De acordo com Ribeiro e Caten (2013) o percentual de não conformes pode ser comparado com as expectativas e metas gerenciais, gerando um índice de capacidade Cp, dado pela equação (14).
Cp = u meta/ u médio (14)
O resultado do calculo do Cp utilizando a equação (12) foi de 1,53. Logo, Cp > 1 o que significa que o processo de fotocorrosão é capaz. A Figura 10 apresenta a distribuição de probabilidade para o processo de fotocorrosão, onde identificou-se que a probabilidade de uma amostra apresentar um número de não conformidades por unidade inferior ao especificado é de 95,6802 % e superior ao especificado de 4,3198 % . A Figura 11 apresenta a carta de controle para a capacidade do processo 2.
Figura 10 – Distribuição de probabilidade para o processo 2. Fonte: autores (2013).

-----
Figura 11 – Carta de capacidade do processo 2. Fonte: autores (2013).
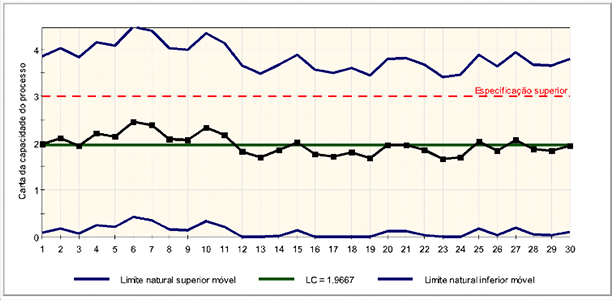
5.5. Função perda do processo de estampagem mecânica
A função perda para o processo de estampagem mecânica foi estimado a partir da equação (10), onde o custo indireto médio por peça encontrado foi de R$ 18,09. Sabendo que são produzidos 1200 peças por mês, estimou-se que o custo indireto por mês é de R$ 22.690,00.
A parcela preponderante da perda é devido à dispersão, pois utilizando a equação (11) calculou-se a natureza do problema de qualidade onde Q ficou próximo de zero. Logo, esse caso é mais difícil de resolver, e geralmente exige ações sobre as causas comuns. A Tabela 4 ilustra os dados utilizados no estudo de perda (L) para o processo1.
Tabela 4 – Perda do processo de estampagem mecânica
Dado |
Valor |
Meta |
0,12 |
Delta |
0,12 |
Ao |
R$ 24,00 |
K |
R$ 1.666,67 |
Média |
0,10430 |
Desvio |
0,022 |
L por peça |
R$ 18,909 |
L n=1200 |
R$ 22.690,964 |
Fonte: autores (2013).
5.6 Função perda do processo de fotocorrosão
A função perda para o processo de fotocorrosão foi estimado a partir da equação (10), onde o custo indireto médio por peça encontrado foi de R$ 340,89. Sabendo que são produzidos 150 peças por mês, estimou-se que o custo indireto por mês é de R$ 51.133,00.
A parcela preponderante da perda é devido à dispersão, pois utilizando a equação (11) calculou-se a natureza do problema de qualidade onde Q ficou próximo de zero. Logo, esse caso é mais difícil de resolver, e geralmente exige ações sobre as causas comuns. A Tabela 5 ilustra os dados utilizados no estudo de perda (L) para o processo 2.
Tabela 5 - Perda do processo de fotocorrosão
Dado |
Valor |
meta |
3 |
média |
1,9667 |
desvio |
0,62716 |
Ao |
R$ 85,00 |
Delta |
1 |
K |
R$ 85,00 |
L |
R$ 362,19 |
Ln=150 |
R$ 54.329,17 |
Fonte: autores (2013).
6. Conclusão
Neste trabalho foi realizado o estudo de estabilidade e capacidade e função perda de dois processos produtivos responsáveis pela estampagem de diferentes peças. Os estudos realizados foram focados na estampagem mecânica de etiquetas para botoeiras de elevador e na estampagem por fotocorrosão de peças de precisão.
No que diz respeito ao estudo de estabilidade, o processo por estampagem mecânica comportou-se de forma instável, pois apresentou causas especiais. Já o processo por fotocorrosão teve um comportamento estável não apresentando causas especiais, possivelmente por ser mais automatizado. Na análise de capacidades os dois processos apresentaram um índice de capacidade maior que 1, logo, foram caracterizados como potencialmente capazes.
Quanto o estudo da função perda, os dois processos apresentaram prejuízo com retrabalho ou substituição de peças não conformes. Identificou-se que o processo de fotocorrosão gera tem uma perda monetária maior, logo, apresenta um custo indireto por mês também maior em relação ao processo de estampagem mecânica. Ainda verificou-se que, para os dois processos, a parcela preponderante da perda é devido a dispersão. Em função disso os problemas nos processos são mais difíceis de resolver, pois geralmente exigem ações sobre as causas comuns. Dessa maneira, pode-se afirmar que a análise trouxe informações de grande importância, que podem ser usadas caso a indústria deseje otimizar os processos.
Referências bibliográficas
CORTIVO, Z.D. Aplicação do controle estatístico de processo em sequencias curtas de produção e análise estatística de processo através do planejamento econômico. Dissertação de mestrado, para obtenção do grau de Mestre em Ciências, pelo Programa de Pós-Graduação em Métodos Numéricos em Engenharia, Universidade Federal do Paraná, Curitiba, 05 de outubro de 2005.
MIYATA, H.H.; BARRETO, A.; GOMES, A.C.S.; MORAIS, M.F. Controle estatístico do processo na produção de circuitos eletrônicos. In: XXX Encontro Nacional de Engenheiros de Produção, 12 a 15 de outubro de 2010, São Carlos, São Paulo.
MONTGOMERY, D. Introdução ao controle estatístico da qualidade. 4ª ed. Rio de Janeiro: Ed. LTC- Livros Técnicos Científicos, 2009.
RIBEIRO, J.L.D. ; TEN CATEN, C.S. Série Monográfica Qualidade: Controle Estatístico do Processo. Porto Alegre: FEENG/UFRGS, 2013.
SALDANHA, P. ; ROTHE, C. K. ; BENEDETT, F. R. ; PACHECO, D. A. J. ; JUNG, C. F. ; CATEN, C. S. T. Analisando a aplicação do Controle Estatístico de Processos na indústria química: um estudo de caso. Espacios (Caracas), v. 34, p. 1-18, 2013.