1. Introdução
Pesquisas realizadas por educadores pesquisadores como Silveira (2011); Lotério (2011); Nunes (2005); Santos (2005) entre outros, têm apontado dificuldades relacionadas à aquisição do conceito de fração, tanto no ensino, quanto na aprendizagem. Atribuem tal situação a ênfase exagerada em procedimentos e algoritmos e insistência generalizada em traduzir o conceito de números fracionários utilizando apenas o significado parte-todo, a partir de sua representação a/b com “a”, “b” inteiros e “b” diferente de zero.
Estas dificuldades encontradas por professores e alunos em relação ao processo de ensino e aprendizagem dos números fracionários têm origem, na maioria das vezes, em um processo de ensino voltado apenas para a memorização de algoritmos sem a compreensão de seus significados.
Para Lorenzato (2008) e Mediano (2008), o ensino voltado apenas para memorização de definições e regras sem a devida compreensão não favorece a aprendizagem, justificando-se assim a necessidade de se explorar o ensino de frações a partir de situações-problemas que possibilitem ao aluno compreender as definições e perceber as regras utilizadas nos algoritmos como a generalização de um padrão. Destaca-se que a generalização de um padrão com significado corresponde à sistematização de um conteúdo e facilita a resolução de outros problemas semelhantes em diferentes contextos.
Nesta perspectiva e com vistas a superar as dificuldades encontradas tanto por professores quanto por alunos em relação ao conteúdo de frações, sugere-se a abordagem do conceito de frações nos Anos Iniciais do Ensino Fundamental a partir da ideia de fração como medida. Isso não significa que outras ideias não possam e não devam ser exploradas.
Esta proposta é uma tentativa de superar o conceito equivocado de fração como uma relação de dois números naturais (um em cima e outro embaixo) que aparece especialmente quando os alunos resolvem as operações de adição e subtração de fração somando/subtraindo numeradores e denominadores entre si, e possibilitar a compreensão de fração como um número que pode representar parte/partes de um inteiro, um número inteiro ou mais que um inteiro/inteiros.
A abordagem do conceito de fração como medida não se faz por um caminho de cálculos e expressões complicadas, mas pela conexão que se estabelece com as medidas de comprimento que está diretamente relacionado à origem das frações.
Segundo Moisés, Lima (2010) os antigos egípcios criaram uma unidade de medida de comprimento para demarcar os terrenos destinados ao plantio, o que mostra que as medições surgiram a partir de uma necessidade operacional. Esta unidade padrão foi representada por uma corda, também chamada de “medida do faraó”.
Os “esticadores de corda” utilizavam a corda considerada como unidade padrão, para fazer a medição do comprimento do terreno. Para tanto verificavam quantas vezes a corda estava contida no comprimento do terreno e, quando sobrava um pedaço do terreno que não tinha comprimento suficiente para marcar como mais uma unidade de medida, eles dobravam a corda em tantas partes iguais quantas vezes fossem necessárias para marcar o pedaço do terreno que sobrou.
Assim, se para medir o comprimento do terreno fossem necessárias 9 cordas os “esticadores de corda” registravam 9 vezes a medida da corda e, se a sobra do comprimento correspondesse a um pedaço da corda que havia sido dobrada em três partes iguais, registravam 1/3 da unidade padrão, portanto, a medida do comprimento do terreno era de 9 unidades mais 1/3 da medida padrão.
Neste exemplo, percebe-se que as frações surgiram dentro de um contexto histórico partindo da necessidade de um povo, e é importante que este seja o ponto de partida para o professor introduzir o conceito de fração e, na sequência, que este conceito seja ampliado e relacionado com as práticas sociais atuais.
Lins, Silva (2008, p. 10) fazem uma analogia interessante entre as unidades de medida de comprimento e as frações unitárias, explicitando que para indicar o comprimento de uma mesa de 2 metros, a representação algorítmica de “quanto” mede a mesa é realizada pelo algarismo (2) e de que “tipo” é a unidade de medida (metro). Se fosse dito que o comprimento da mesa era 200 cm então o “quanto” seria 200 e o “tipo” seria centímetros. Transferindo este raciocínio para o conceito de frações, pode-se considerar que “elas [as frações] são o resultado de se medir alguma coisa, usando como referência uma parte da unidade”.
Observa-se que muda o enfoque da representação de frações com o significado parte-todo a partir de sua representação a/b com “a”, “b” inteiros e “b” diferente de zero e considera-se a fração unitária como unidade de medida. Assim, se um bolo for dividido em 6 partes iguais, cada parte do bolo é representada por uma fração unitária (1/6) e o denominador indica o “tipo” de pedaço que está sendo utilizado como unidade de medida. Para representar que foram comidos 5 pedaços do “tipo” 1/6 obtém-se: 5 x 1/6 = 5/6, em que o “quanto” é 5 e o “tipo” é 1/6 (cinco pedaços do tipo 1/6 que corresponde a 5/6).
Nesta perspectiva, no presente artigo foi analisado um recorte do Curso de Formação Continuada para professores dos Anos Iniciais do Ensino Fundamental denominado “As frações e seus diferentes significados”, delimitando-se a abordagem da ideia de fração como unidade de medida, fração unitária e equivalência de frações.
2. Fundamentação teórica
As frações fazem parte do conjunto dos números racionais e têm seu ensino formalmente estabelecido para os dois anos finais do primeiro segmento do Ensino Fundamental.
Conforme orientações dos Parâmetros Curriculares Nacionais (PCN), nos anos finais do primeiro segmento do Ensino Fundamental devem ser apresentadas aos alunos situações-problemas que não são solucionadas com o uso dos números naturais, possibilitando, assim, uma aproximação da noção de número racional, a compreensão de alguns de seus significados e de suas representações, fracionária e decimal (BRASIL, 2001, p.83).
No segundo segmento do Ensino Fundamental, de acordo com as indicações das Diretrizes Curriculares da Educação Básica do Estado do Paraná (DCE), esses conhecimentos devem ser ampliados, especialmente no 6º e 7º anos do Ensino Fundamental, partindo do princípio que a construção do conceito de número fracionário se dá a partir da relação que o aluno estabelece entre os conhecimentos prévios (já adquiridos) e o novo conhecimento.
Esta orientação dá ideia de uma sequência de aprendizados que permitiria aos alunos a construção do conceito de números fracionários à medida que avançam nos níveis de escolarização. No entanto, percebe-se que esta construção não acontece e muitos alunos que cursam o Ensino Médio ainda apresentam desconhecimento do conceito de números fracionários.
Para Vygotsky (2008) o termo conceito expressa como se assimila o conhecimento sobre alguma coisa, podendo ser dividido em dois tipos: cotidiano e científico, exigindo dos estudantes experiências, atitudes e caminhos diferentes a serem percorridos durante a aprendizagem. Assim, os conceitos cotidianos são resultantes das atividades práticas das pessoas em suas interações sociais imediatas, enquanto os conceitos científicos são adquiridos por meio do ensino, resultantes de um sistema organizado sistematicamente, relevantes nas sociedades letradas.
Em consonância com outros educadores pesquisadores, Vygotsky (2008) comenta que embora os conceitos científicos sejam transmitidos em situações formais de ensino, eles não são assimilados em sua forma definitiva. Assim, nas futuras experiências da criança a tendência é que os conceitos cotidianos entrem em confronto com uma situação concreta de aprendizagem. Em relação aos conceitos científicos, estes agregam elementos a partir das experiências cotidianas e caminham em direção a um nível mais aprimorado e refinado, convergindo a um ponto comum.
A criança adquire consciência dos seus conceitos espontâneos relativamente tarde; a capacidade de defini-los por meio de palavras, de operar com eles à vontade, aparece muito tempo depois de ter adquirido os conceitos. Ela possui o conceito (isto é, conhece o objeto ao qual o conceito se refere), mas não está consciente de seu próprio pensamento. O desenvolvimento de um conceito científico, por outro lado, geralmente começa com sua definição verbal e com sua aplicação em operações não espontâneas. (VYGOTSKY, 2008, p.134).
Assim os conceitos cotidianos têm um desenvolvimento ascendente em direção aos científicos e, os conceitos científicos apresentam um desenvolvimento decrescente em relação aos conceitos cotidianos. Isto decorre das diferentes formas pelas quais os dois tipos de conceitos surgem. Pode-se remeter a origem de um conceito espontâneo a um confronto com uma situação concreta, ao passo que um conceito científico envolve, desde o início, uma atitude “mediada” em relação a seu objeto (VYGOTSKY, 2008, p.135).
Nesse sentido, a construção do conceito de frações, oficialmente apresentado como conteúdo nos PCN e nas DCE, com orientações para o trabalho nos dois anos finais do primeiro segmento (4o e 5o ano) e nos dois anos iniciais do segundo segmento do Ensino Fundamental (6o e 7o ano) numa perspectiva de contextualização a partir de situações-problemas, constitui-se em um conceito científico.
Educadores que seguem a linha de pensamento de Vygotsky (2008), citando como exemplo Almeida (2010, p.3) entendem que somente torna-se possível ampliar/refinar o conhecimento dos alunos se houver entendimento de que “é indispensável que o educador investigue os conceitos cotidianos dos alunos acerca do conteúdo que pretende ensinar, introduza os conceitos científicos a ele relacionados e promova a interação entre esses dois tipos de conceitos.”
Vygotsky (2008), considera que a construção do conceito é um processo dinâmico no desenvolvimento das estruturas cognitivas do indivíduo, conceito este que se completa no decorrer do tempo, ganhando novos elementos.
A ampliação desta visão vygotskyana defronta-se com o campo conceitual defendido por Vergnaud (1994), que propõe estudar um campo conceitual ao invés de um conceito, visto que, para ele em uma situação-problema qualquer, nunca um conceito aparece sozinho, são sempre vários os conceitos envolvidos. Explica-se esta teoria de campo conceitual em três argumentos,
- um conceito não se forma dentro de um só tipo de situações;
- uma situação não se analisa com um só conceito;
- a construção e apropriação de todas as propriedades de um conceito ou todos os aspectos de uma situação é um processo de muito fôlego que se estende ao longo dos anos, às vezes uma dezena de anos, com analogias e mal entendidos entre situações, entre concepções, entre procedimentos, entre significantes (Vergnaud, 1983 apud MOREIRA, 2004, p. 10).
Neste contexto em circunstância relacionada à Matemática podem ser identificados vários conceitos já adquiridos pelo aluno, quando se inicia o aprendizado de um conteúdo, o que deve ser aproveitado para facilitar a resolução de problemas. No exemplo “João possuía 5 bolinhas de gude, ganhou mais duas. Quantas bolinhas possui agora?”, seguindo a linha de pensamento de Vergnaud (1994) um aluno que já adquiriu noções de adição e de tempo, pode levantar os seguintes conceitos:
- Temporalidade: possuía = tempo passado, possui agora = tempo presente,
- Contagem: depois do número cinco vem o número seis e depois vem o número sete.
Tem-se assim, que a resolução de um problema representa uma situação em que se faz uso de vários conceitos que vão surgindo aguçados pelo raciocínio do aluno. Em relação aos conceitos matemáticos, Nunes et al (2005, p. 58) descrevem o posicionamento do pesquisador Hans Freudenthal que considera todo conceito matemático ligado,
[...] a alguma realidade fenomenológica, de onde podemos partir para expandir o conceito do aluno. Há sempre novas possibilidades de expansão do conceito, englobando novos instrumentos de raciocínio, novas realidades fenomenológicas, ou novas relações lógicas e matemáticas. De certa forma ninguém seria completamente ignorante com relação aos conceitos matemáticos que ensinamos na escola, porque todos temos alguma vivência relevante, algum esquema de ação relevante. Da mesma forma, ninguém esgotaria esses conceitos durante o período escolar, pois poderíamos pensar em outras formas de representação ou outro nível de abstração envolvendo o mesmo conceito. O desafio para o professor é encontrar os pontos de partida e delinear objetivos para o desenvolvimento do conceito durante o período escolar.
Para que o professor tenha esta percepção, ele precisa estar em contínua formação para aperfeiçoar suas estratégias de ensino em função dos conhecimentos prévios dos alunos. Para tanto, o professor também precisa “saber” o conteúdo de forma ampla, não apenas pelo sistema mecanizado e técnico, mas com um conhecimento que lhe permita fazer conexões com a prática social.
Considera-se, portanto, que o processo de ensino e aprendizagem se dá a partir das relações que se estabelece entre os campos conceituais e a prática social. Nesta perspectiva, propõe-seo estudo de frações em um Curso de Formação Continuada para Professores.
3. Contexto da pesquisa
Para a realização do Curso de Formação Continuada para Professores dos Anos Iniciais “As frações e seus diferentes significados”, foram convidados professores que atuavam em uma Rede Municipal de Ensino com alunos do 5º ano do Ensino Fundamental, sendo inscritos na primeira etapa, apenas os 20 primeiros professores que entregaram a ficha de inscrição, os quais por uma questão de ética não são nominados e, suas respostas e desempenho são avaliados como o todo de uma amostra. O Curso foi realizado em período contrário ao da jornada de trabalho destes professores e teve duração de 40 horas, distribuídas em 10 oficinas de 4 horas.
Para fazer um diagnóstico do que trabalhar e de como abordar o conteúdo de frações no Curso inicialmente foi aplicado um questionário com perguntas abertas e fechadas para identificar as características da formação inicial, da história profissional e da prática pedagógica destes professores em sala de aula.
Também foram aplicados dois testes: o pré-teste aplicado antes do início das oficinas e o pós-teste aplicado após o término das oficinas com o objetivo de avaliar o nível de conhecimento dos professores em relação ao conteúdo de frações.
Os resultados do questionário e do pré-teste forneceram indicativos de quais eram as lacunas existentes nos conhecimentos dos professores e forneceram dados que demonstraram a necessidade de intervenção pedagógica no que se refere aos conceitos e estratégias de ensino de frações. Mediante análise das dificuldades encontradas pelos professores foram planejadas oficinas pedagógicas que foram avaliadas ao final do curso, mediante a aplicação do pós-teste.
Importante destacar, que no presente estudo analisa-se um recorte do Curso “As frações e seus diferentes significados”, delimitando-se a abordagem do conteúdo de frações com enfoque no aprofundamento conceitual e nas estratégias de ensino e não na análise dos instrumentos utilizados para o diagnóstico.
4. Encaminhamento metodológico
A organização das oficinas pautou-se em um diagnóstico inicial que revelou a ausência de um trabalho significativo em relação à construção do conceito de fração nos Anos Iniciais do Ensino Fundamental. Assim, o objetivo das oficinas foi proporcionar aos Professores Cursistas o aprofundamento conceitual em relação aos números fracionários e a vivência de práticas de ensino, incluindo a ideia de fração como unidade de medida, por meio do estudo de textos e a análise/resolução de exercícios numa perspectiva dialógica.
Os procedimentos adotados para o desenvolvimento do curso foram embasados na tese intitulada Cenário para Investigação de Skovsmose (2000) que considera o espaço de ensino e aprendizagem. Espaço este, em que o aprendiz tem a oportunidade de desenvolver processos de criação e investigação, e as estratégias de resolução de um problema não são únicas, o que realmente importa é a reflexão e discussão dos processos utilizados para se chegar ao resultado.
Nesta perspectiva, no presente trabalho desenvolveu-se um projeto de investigação abrangendo os momentos pedagógicos apontados por Delizoicov, Angotti, Pernambuco (2009), ou seja, a problematização inicial, a organização do conhecimento e, por fim, a aplicação do conhecimento. A problematização inicial e a organização/sistematização do conhecimento aconteceram durante as oficinas com a mediação do Professor Formador e a aplicação ocorreu na ocasião em que os Professores Cursistas planejaram e desenvolveram aulas com seus alunos tendo como base as discussões e atividades desenvolvidas no curso. Para clarificar, na sequência, discorre-se sobre alguns momentos considerados como relevantes nas oficinas.
Na primeira oficina foi estabelecido um diálogo entre o Professor Formador e os Professores Cursistas, a partir da afirmação: “Uma mesa tem 2 metros de comprimento”, conforme segue:
- Quanto mede esta mesa? (Formador)
- Dois. (Cursistas)
- Dois palmos? Dois centímetros? Dois, o quê? (Formador)
- Metros. (Cursistas)
A relação dialógica estabelecida entre o Professor Formador e os Professores Cursistas favoreceu um espaço de aprendizagem, estabelecendo-se inicialmente que a indicação de “quanto” mede a mesa se dá pela representação do algarismo 2 (dois) e que a unidade de medida do comprimento da mesa é o metro. Se a afirmação fosse “Uma mesa tem 200 cm de comprimento”, o “quanto” mudaria para 200 e a unidade e medida para centímetros, representação esta encontrada na prática social. Este diálogo se deu em uma perspectiva que “não teve como objetivo ensinar os alunos [professores] a usarem modelos matemáticos, mas antes, questionar o porquê, o como, o para quê e o quanto dessa utilização matemática associada aos modelos reguladores da sociedade global em que vivemos”(SILVA, 2007, p. 51).
As perguntas formuladas pelo Professor Formador tiveram como objetivo mostrar aos Professores Cursistas que para respondê-las não precisariam utilizar definições advindas de um ensino baseado na repetição de algoritmos, mas que as respostas poderiam ser dadas a partir da prática social, o que torna a aprendizagem mais interessante e significativa. Isso não quer dizer que as definições não sejam importantes, mas que é necessário estabelecer conexões com a prática social, especialmente nos Anos Iniciais do Ensino Fundamental. Ainda, segundo Baier (2005) ao se estabelecer a dialogicidade entre professor e alunos, o educador possibilita ao aprendiz buscar formas alternativas para construir seu conhecimento.
No diálogo estabelecido entre o Professor Formador e os Professores Cursistas conclui-se que para medir é necessário conhecer o “quanto” e a “unidade de medida utilizada”. Este conhecimento facilita a ação de estabelecer a analogia entre o conceito de medida de comprimento e a ideia de fração como resultado de uma medição.
Para fazer a analogia entre o conceito de medida de comprimento e as frações, inicialmente o Professor Formador propôs uma atividade com o objetivo de definir fração unitária. Para tanto, foram representados três retângulos divididos em partes iguais, conforme se visualiza na Figura 1.

Figura 1 – Exemplos de frações como unidade de medida
A partir dos retângulos representados na Figura 1, estabeleceu-se o diálogo entre o Professor Formador e os Professores Cursisas:
- Em quantas partes o retângulo A da Figura 1 foi dividido? (Formador)
- Foi dividido em duas partes iguais. (Cursistas)
- Como pode ser representada cada uma destas partes do retângulo A? (Formador)
- Pela fração 1/2 (Cursistas)
- E o retângulo B foi dividido em quantas partes? (Formador)
- Em três partes iguais. (Cursistas)
- E o retângulo C, em quantas partes foi dividido? (Formador)
- Em quatro partes iguais. (Cursistas)
- As partes representadas no retângulo A e no retângulo B são do mesmo "tipo"? ( Formador)
- Não, no retângulo A é do "tipo" 1/2 e no retângulo B é do "tipo" 1/3. (Cursistas)
- Então, o que determina o "tipo"da fração? (Formador)
- O denominador. Ele indica o "tipo" de divisão realizada. (Cursistas)
A partir deste diálogo, evidenciou-se que o denominador indica o "tipo" de divisão realizada, e que ao representar apenas uma destas partes obtêm-se as frações unitárias 1/2, 1/3, 1/4, que podem ser consideradas como unidades de medida.
Assim, para indicar o quanto de um bolo foi comido, por exemplo, é necessário dividi-lo em partes iguais em relação à área e identificar a fração unitária que será considerada como unidade de medida.
Aproveitando os exemplos que são utilizados nos livros didáticos, remete-se a situação em que um bolo foi dividido em 6 partes iguais e André comeu 5 destas partes (representadas pela cor vermelha), conforme se visualiza na Figura 2.

Figura 2: Representação da fração 5/6
Considerando-se o retângulo representado na Figura 2 como sendo uma forma de bolo que foi dividida em partes iguais e que as coloridas de vermelho foram comidas, tem-se:
- que cada pedaço é do "tipo" um sexto, representado pela fração 1/6.
- que o “quanto” de pedaços tomados é representado pelo número 5.
Assim, cinco pedaços do "tipo" sextos correspondem a 5x1/6 = 5/6.
Neste exemplo, ao explorar os termos “quanto” (5) e de que "tipo" (sextos) de forma análoga à utilizada com as medidas de comprimento, as frações foram conceituadas como sendo o resultado de medir alguma coisa, usando como unidade de medida a fração unitária. Tal situação enquadra-se na estrutura da teoria dos campos conceituais de Vergnaud (1994) ao serem abordados os conceitos de medida, unidade fundamental de medida, divisão de uma superfície plana em partes iguais em relação a área, fração unitária e multiplicação, conceitos estes "conectados uns aos outros e, provavelmente, entrelaçados”(MOREIRA, 2004, p. 8).
Para complemento e aprofundamento conceitual, os professores realizaram o estudo do Texto “Um pouco mais sobre o que são frações” que é o resultado do trabalho realizado pelos professores pesquisadores Rômulo Campos Lins e Heloísa da Silva da Universidade Estadual Paulista, disponibilizados no Fascículo de Frações do Programa de Formação Continuada para Professores dos Anos Iniciais Pró-Letramento Matemática que versa sobre a relação existente entre as frações e as medidas, ressaltando que o denominador de uma fração indica o “tipo”de divisão que foi realizada e o numerador indica a quantidade de partes consideradas.
Neste texto, Lins, Silva (2008) procuram contribuir com farto material didático para firmar o conceito de fração como medida, declarando que esta não é uma prática muito utilizada no Brasil, fato este que pôde ser observado mediante análise das respostas obtidas por meio do questionário e do pré-teste indicando que os professores desconheciam a ideia de fração como medida e confirmado pela verbalização de um Professor Cursista:
Gostei do texto, é a primeira vez que tenho contato com fração unitária vista como unidade de medida. Achei interessante a analogia com as medidas de comprimento. A cada encontro percebo que, o que pensava que dominava com tranquilidade, na verdade era mecânico. (R.A.S.)
Com esta declaração percebe-se que, nas escolas, os professores não abordam o conceito de fração como medida, o que pode estar contribuindo para que os alunos não identifiquem a fração como um número racional. Segundo Lorenzato (2008), quando o professor não sabe um conteúdo ele não consegue ensinar. Assim, se o professor conhece apenas os procedimentos algorítmicos ele não consegue estabelecer conexões entre o conteúdo abordado e seu uso no contexto social ficando o ensino restrito às técnicas operatórias.
Na sequência, com o objetivo de discutir, na comparação de frações, a necessidade de se considerar o mesmo todo ou um inteiro de mesmo tamanho para representá-las, o Professor Formador fez o seguinte questionamento: “1/4 em qualquer situação será sempre igual a 1/4?”
Apesar de a resposta positiva parecer óbvia, no ensino de frações a resposta pode ser negativa em alguns contextos. Por exemplo, 1/4 de um bolo de 2 kg não é igual a 1/4 de um bolo de 4 kg mesmo que a representação fracionária seja a mesma, como pode ser visualizado na Figura 3.
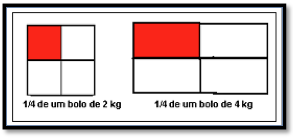
Figura 3 – Representação de 1/4 de dois bolos: um de 2kg e outro de 4kg
Os professores, ao perceberem que as frações unitárias representam a parte de um todo e que essas partes só podem ser comparadas se os inteiros forem iguais, passaram a refletir sobre a prática em sala de aula e mostraram, conforme indica Lins e Silva (2008) “escolhas didáticas”. Podem-se observar estes apontamentos no posicionamento de um Professor Cursista,
As minhas aulas a partir de agora serão mais interessantes, estou compreendendo que não basta trabalhar com as representações, é necessário problematizar, visualizar e depois generalizar... .Se os alunos compreenderem bem os conceitos e algoritmos não encontrarão dificuldades depois quando estiverem operando algebricamente. (A.D.)
O posicionamento deste professor vai ao encontro das sugestões de Lins e Silva (2008, p. 12) quando comenta que “é preciso pensar no que vem adiante, e não apenas no que parece ser mais fácil de explicar naquele momento”. Assim, se os professores compreenderem e assumirem o ensino dos números fracionários a partir da ideia de fração unitária como unidade de medida poderão ajudar “as crianças a perceberem fração como um número, e não apenas como um símbolo que junta dois números...” (LINS, SILVA, 2008, p. 11).
Nesta mesma perspectiva, o Professor Formador, com o objetivo de reforçar a ideia de fração unitária e de oportunizar a vivência de diferentes estratégias de ensino, propôs aos Professores Cursistas que resolvessem o exercício descrito na sequência:
Exercício 1: Usando 6 tiras de papel de 3 cm por 15 cm, represente as frações unitárias: 1/2; 1/3; 1/5 e 1/15. Na sequência coloque as frações em ordem crescente.
Valendo-se da alternativa didática de representar as frações por meio da divisão de superfícies planas, os Professores Cursistas resolveram o exercício, conforme se visualiza na Figura 4.

Figura 4 – Representação de frações em inteiros do mesmo tamanho
Os Professores Cursistas não encontraram dificuldades para a representação das frações 1/2, 1/3, 1/5 e 1/15 nas tiras de papel e alguns se posicionaram em relação ao comprimento da tira (15 cm) e a divisão por 2, 3, 5 e 15, conforme o consta na fala de um dos professores,
Como a tira de papel tem 15 cm de comprimento, os alunos não terão dificuldades na divisão. Para dividir em duas partes iguais é só dobrar a tira de papel ao meio e para dividir por 3, 5 e 15 o resultado é exato. Isso facilita a representação, especialmente daqueles [dos alunos] que ainda encontram dificuldades em medir com precisão. (M.S.)
Após uma breve discussão estabelecida entre os Professores Cursistas em relação à aplicabilidade do exercício em sala de aula, um professor verbalizou:
Na prática quando as crianças fazem a representação das frações por meio de desenho no caderno não há cuidado de dividir em partes iguais em relação à área, é apenas uma repartição. Um conceito equivocado, e o pior é que eu pensava que estava tudo bem (R.A)
Segundo Freire (1998) em sua visão de educar para a liberdade, o professor não deve ter vergonha em assumir que não domina determinado assunto, pois é na convivência, no diálogo, na espontaneidade do aprendizado que se adquire conhecimentos que possibilitam diferentes formas de agir pedagogicamente.
Observa-se que a utilização da representação de frações em figuras geométricas planas é comum nos livros didáticos e na prática escolar, porém pouca ênfase é dada ao fato das divisões serem em partes iguais em relação à área. Este detalhe, conforme explica Lins e Silva (2008) é o de “refinar” a capacidade do aluno para lidar com situações que envolvem o conhecimento de frações.
Para Lotério (2011, p. 201), “se por um lado surge por parte dos alunos uma dificuldade grande em relacionar o que estão estudando com seus anseios, muitas vezes a teoria aparece desconectada da realidade atual”, por isso deve haver um entrelaçamento do currículo estabelecido pela escola com a leitura do mundo que o aluno faz em seu cotidiano.
Este posicionamento coloca em evidência a necessidade de um processo de ensino que priorize a articulação entre os eixos da Matemática e as conexões com as diversas áreas do conhecimento. Segundo Lorenzato (2008, p. 60) é “falacioso pensar que, conhecendo parte do todo, já se conhece o todo. Por isto todos os campos da matemática previstos no currículo oficial devem ser ensinados, e mais, de modo integrado.”
Nesta perspectiva, ao proporcionar a formação continuada dialógica, identificando pontos de conexão entre os campos conceituais e estimulando os professores a trabalharem esses conceitos com seus alunos é possível (re)significar o processo de ensino e aprendizagem, conforme se observa na fala de um dos professores,
Eu propus o exercício das tiras de papel na minha turma, todos os alunos resolveram e compreenderam porque 1/2 representa uma área maior do que 1/5. Estou realizada em explicar e discutir com eles a necessidade de representar frações em retângulos de mesmo tamanho para posterior comparação. Depois de ter trabalhado no concreto foi surpreendente observar os alunos resolvendo os exercícios do livro, eles discutiam, argumentavam, representavam e acertavam. (A.S.)
A função do professor no processo de ensino é a de planejar estratégias para que o aluno possa construir, (re)construir, ampliar ou refinar os conceitos por meio de situações-problemas, buscando atuar na Zona de Desenvolvimento Potencial enunciada por Vygotsky (2008), ou seja, partindo do que o aluno já conhece para alçar a patamares mais elevados em relação a compreensão dos conteúdos abordados. Um momento importante nestas estratégias é o diálogo. Ponte (2003) comenta que pela dialogicidade o professor induz o aluno à investigação matemática e pode incentivá-lo a buscar o conhecimento por meio da compreensão de conceitos e pela relação que estabelece com a prática social.
Ponte (2003) alerta que uma investigação formulada e embasada na realidade do aluno serve como ponto de partida, tanto para o desenvolvimento de competências, como também para aprender novos conceitos. Neste processo de desenvolver novos conceitos, o aluno vai se tornando sujeito de processos e assim sentindo-se responsável por novas descobertas.
O professor ao vivenciar práticas pedagógicas que favoreçam a compreensão de algoritmos e o aprofundamento conceitual em situações problematizadas também se sente desafiado a buscar o aperfeiçoamento profissional e a planejar aulas contextualizadas. Esta situação pode ser percebida na fala do professor,
Pelo relato do Professor Cursista e pelos resultados da pesquisa sobre a Formação de Professores dos Anos Iniciais realizada por Pires (2002), percebe-se a necessidade do professor vivenciar novas estratégias de ensino nos cursos de Formação Inicial e Continuada. Isto não significa que o professor vai reproduzir os mesmos procedimentos com seus alunos, mas que terá outras vivências para além daquela que normalmente utiliza como referência.
Nesta mesma perspectiva, Fiorentini, Nacarato (2005) apontam a necessidade de o professor construir a partir de sua prática de sala de aula, objetos de investigação e reflexão, não se prendendo apenas aos aportes teóricos adquiridos em sua vida acadêmica, mas buscando aprimorá-los com o objetivo de tornar o ensino de Matemática significativo e de instrumentalizar os alunos com estratégias de pensamento, aprofundamento conceitual e habilidades algorítmicas para a resolução de problemas no contexto escolar e na prática social.
Buscando avançar no estudo de frações, a partir da construção do conceito de fração unitária é possível ampliar o conhecimento sobre o conteúdo, abordando-se a equivalência de frações que foi pontuada por Lins, Silva (2008, p. 17) como sendo a “ideia mais importante” porque permite “comparar, somar e subtrair frações, além de ajudar a entender como frações se relacionam a razões e proporções...”
Assim, para a abordagem da equivalência de frações, inicialmente, foi proposto aos Professores Cursistas o estudo do texto “Como criar frações equivalentes a uma fração que já tenho?” (LINS, SILVA, 2008, p. 18), no qual constam dois procedimentos para se obter frações equivalentes.
O primeiro procedimento consiste em multiplicar o numerador e o denominador de uma fração por um mesmo número diferente de zero. Exemplifica-se este procedimento com um bolo que corresponde ao “inteiro” e à fração 1/2 que representa a metade do bolo, conforme mostra a Figura 5.
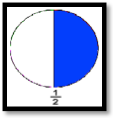
Figura 5 – Representação de 1/2 de um bolo
Para encontrar uma fração equivalente a 1/2, multiplica-se o numerador e o denominador da fração por 2 e obtém-se a fração 2/4.
Este procedimento numericamente é representado por:
![]()
Visualiza-se que ao multiplicar a fração 1/2 por 2, cada metade do bolo foi dividida em duas partes, assim, o bolo que inicialmente havia sido dividido em duas partes ficou dividido em 4 partes e cada uma dessas partes é duas vezes menor do que a parte inicialmente considerada (1/2 do todo), conforme ilustra a Figura 6.
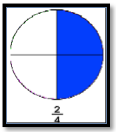
Figura 6 – Representação de 2/4 de um bolo
Comparando-se a representação da Figura 5 com a Figura 6, observa-se que, marcadas pela cor azul, as frações 1/2 e 2/4 correspondem à mesma porção de bolo, portanto são frações equivalentes.
Da mesma forma, ao multiplicar-se o numerador e o denominador da fração 1/2 pelo número 4 obtém-se a fração 4/8. Este procedimento numericamente é representado por:
![]()
Ao multiplicar a fração 1/2 por 4, cada metade do bolo foi dividida em 4 partes iguais, assim, o bolo que inicialmente havia sido dividido em duas partes ficou dividido em 8 partes e cada uma dessas partes é quatro vezes menor do que a parte inicialmente considerada (1/2 do todo), conforme se visualiza na Figura 7.

Figura 7 – Representação de 4/8 de um bolo
Comparando-se a representação das Figuras 5, 6 e 7, observa-se que, marcadas pela cor azul, as frações 1/2, 2/4 e 4/8 correspondem à mesma porção de bolo, portanto são frações equivalentes entre si.
O segundo procedimento consiste em dividir o numerador e o denominador de uma fração por um mesmo número diferente de zero. Com este procedimento obtêm-se frações equivalentes mais simples, ou seja, a simplificação de frações. Assim, para encontrar uma fração equivalente a 2/4, por exemplo, divide-se o numerador e denominador pelo número 2 e obtém-se a fração 1/2.
Em relação ao ensino de frações para alunos dos Anos Iniciais do Ensino Fundamental, Lins, Silva (2008, p.16) perceberam em suas pesquisas que “é melhor trabalhar a compreensão das técnicas do que sobrecarregar as crianças com contas que não fazem sentido para elas” e que este trabalho “deve ser fundamentado em duas ideias centrais, as de frações equivalentes e frações unitárias”.
Com o objetivo de reforçar o conceito de frações unitárias e frações equivalentes por meio da vivência deuma prática pedagógica, o Professor Formador propôs aos Professores Cursistas que resolvessem o exercício que segue:
Exercício 2: Utilizando 9 tiras de papel cartão de cores diferentes e de mesma medida (sugestão: 2 x 30 cm), realize as seguintes atividades:
A- Divida cada uma das 9 tiras de papel cartão em partes da seguinte forma:
- a primeira em uma parte;
- a segunda em duas partes iguais;
- a terceira em três partes iguais;
- a quarta em quatro partes iguais;
- a quinta em cinco partes iguais;
- a sexta em 6 partes iguais;
- a sétima em 10 partes iguais;
- a oitava em 15 partes iguais; e,
- a nona em 30 partes iguais.
Para dividir as tiras em partes iguais use a régua ou faça dobraduras.
B- Escreva na extremidade esquerda de cada uma das tiras de papel o “tipo” de divisão que foi realizada por meio de uma fração unitária.
C- Coloque as 9 tiras justapostas (encostadas umas às outras) e identifique as frações que se localizam em pontos coincidentes observando as divisões realizadas no item A.
D- Liste todas as frações que estão no mesmo alinhamento, ou seja, aquelas em que as marcas das divisões coincidem.
A resolução do exercício2 pode ser visualizada na Figura 8, onde no lado esquerdo estão indicadas as frações unitárias que correspondem ao “tipo” de divisão realizada em cada tira de papel.
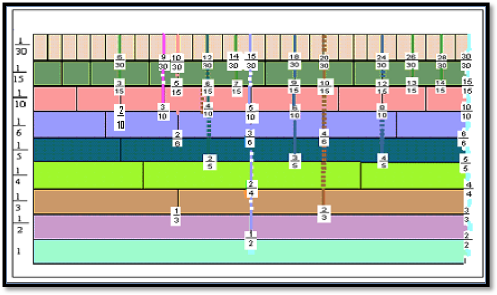
Figura 8 – Representação de frações equivalentes em tiras de papel de mesma dimensão
Este exercício favoreceu algumas reflexões sobre o ensino de frações conforme mostra o trecho do diálogo entre o Professor Formador e um dos Professores Cursistas:
- O que há de significativo neste exercício? (Formador)
- Nada, eu já vi em muitos livros didáticos e é igual aos demais. A diferença está na minha compreensão. (Cursista)
- Compreensão do quê? (Formador)
- Do conceito de fração unitária, da ideia de fração como unidade de medida e agora da equivalência. (Cursista)
A ação de representar as frações: 6/30 (correspondendo a 6 partes da tira que foi dividida em 30 partes), 3/15 (correspondendo a 3 partes da tira que foi dividida em 15 partes) e 2/10 (correspondendo a 2 partes da tira que foi dividido em 10 partes) contribuiu para compreensão da equivalência de frações. Os Professores Cursistas, chegaram à conclusão de que as frações 6/30, 3/15 e 2/10 são equivalentes porque possuem a mesma área e/ou porque correspondem a um ponto comum nas tiras de papel, conforme relato de um dos professores,
Este exercício possibilita a visualização das frações equivalentes, fica fácil identificá-las por meio da comparação, mas é preciso ter atenção na hora de dividir as tiras de papel. Precisamos alertar os alunos quanto à divisão com a máxima precisão possível. (A.S.)
Localizando os pontos de coincidência nas tiras de papel e os identificando por meio de frações, os Professores Cursistas construíram uma lista de frações equivalentes entre si conforme se visualiza no Quadro 1.
1/2=2/4=3/6=6/10=15/30 |
3/5=6/10=9/15=18/30 |
1 = 2/2=3/3=4/4=5/5=6/6=10/10=15/15=30/30 |
2/3=4/6=10/15=20/30 |
3/5=6/30 |
4/5=8/10=12/15=24/30 |
3/10=9/30 |
13/15=26/30 |
2/5=4/10=6/15=12/30 |
14/15=28/30 |
7/15=14/30 |
Quadro 1 – Lista de frações equivalentes entre si
Ao término da primeira oficina que teve como objetivo o estudo das frações unitárias e equivalentes, alguns professores se manifestaram:
Por que ninguém me explicou desse jeito? No meu tempo de estudante era só cálculo e as regras: divida o de cima e o de baixo por um mesmo número, aí você tem a simplificação ou multiplique o de cima e o de baixo e obtenha uma fração equivalente. (M.B.)
Com o estudo do texto e a visualização das frações equivalentes representadas nas folhas de papel, esse conteúdo ficou muito fácil. (R.S.)
Esses posicionamentos forneceram o indicativo de que os professores ainda continuam ensinando a partir do que aprenderam enquanto estudantes, e este fato pode ser mudado ao se propor processos de formação que levem em consideração a prática do professor, o aprofundamento conceitual e as estratégias de ensino.
O domínio conceitual dos conteúdos sistematicamente organizados é fator preponderante para práticas pedagógicas que possibilitem conexões entre os diferentes conteúdos, conforme se percebe na fala de um dos professores:
Se o aluno compreender as equivalências não terá problemas com a adição de frações com denominadores diferentes. No algoritmo convencional precisamos relacionar o cálculo do Mínimo Múltiplo Comum com a equivalência de frações. (R.S.)
Para a abordagem das operações de adição e subtração de frações, inicialmente o Professor Formador propôs aos Professores Cursistas os seguintes questionamentos:
- Por que calculamos o Mínimo Múltiplo Comum para efetuar a adição de frações com denominadores diferentes?
- Existe alguma outra forma de se fazer essa operação sem utilizar o Cálculo do Mínimo Múltiplo Comum? Qual?
- Por que na adição e na subtração com frações não se adicionam/subtraem os denominadores?
Os questionamentos tiveram como objetivo despertar a curiosidade e o interesse dos professores para a leitura do texto “Como somar e subtrair frações?” (LINS e SILVA, 2008, p. 21), que faz uma analogia entre a representação dos resultados da medição de comprimentos e a soma de frações com denominadores diferentes.
Após o estudo do texto "Como somar e subtrair frações" o Professor Formador explicou aos Professores Cursistas que, para se obter, por exemplo, a representação do resultado da medição de 1 metro e 30 centímetros não é possível somar o 1 com o 30, porque são unidades de medidas de tipos diferentes. Assim, para se resolver a operação: 1 m + 30 cm é necessário transformar as unidades de medida em um mesmo “tipo”, ou seja, o metro em centímetros ou os centímetros em metro. A primeira opção consiste em transformar o 1 metro em centímetros (1m = 100 cm) e depois somar os 100 cm com os outros 30 cm, resultando em 130 cm, e a segunda opção consiste em transformar os 30 centímetros em metro (30 cm = 0,3 m) e depois somar o 1 m com 0,3 m resultando em 1,3 m. Observa-se que 130 cm = 1,3 m.
Nesta perspectiva, o Professor Formador esclareceu que, da mesma forma acontece com as frações, não é possível, por exemplo, somar diretamente 2/3 com 5/6, porque são frações de “tipos” diferentes (uma é do “tipo" terço e outra do “tipo" sexto). Para efetuar a soma é necessário transformá-las em frações de mesmo “tipo”.
Como as frações 2/3 e 4/6 são equivalentes, para a adição de 2/3 + 5/6, substitui-se a fração 2/3 pela fração 4/6, ficando: 4/6 + 5/6 = 9/6 (quatro sextos mais 6 sextos = 9 sextos).
A partir do princípio de que só é possível fazer as operações de adição/subtração diretamente com coisas do mesmo "tipo", compreende-se a necessidade de transformar frações que possuem denominadores diferentes em frações com denominadores iguais, reafirmando o significado do denominador, e estabelecendo relação com o cálculo do M.M.C comumente utilizado para se obter frações equivalentes com denominadores comuns, mas poucas vezes entendido. Este entendimento é retratado pela fala de um Professor Cursista,
Realmente, agora consigo compreender porque, por exemplo, no algoritmo da adição nós somamos unidades com unidades, dezenas com dezenas e do 6º ao 9º ano, só podemos somar x com x e não x com y, por exemplo. Legal, um mesmo conceito se aplica em outras situações. (R.A.)
Percebe-se nesta fala o entusiasmo do professor que conseguiu estabelecer conexões entre os conceitos abordados no ensino de frações com outros conteúdos matemáticos, que até então não eram percebidos e, por consequência, sequer mencionados aos alunos.
Segundo Thompson (1997) apud SILVA (2005, p. 33), “qualquer esforço para mudar o ensino de Matemática deve começar por uma compreensão das concepções sustentadas pelos professores e pelo modo como estas estão sendo relacionadas com sua prática pedagógica”. Assim, para preencher as lacunas da formação inicial, torna-se imprescindível oportunizar aos professores vivências de práticas pedagógicas que possibilitem a compreensão de conceitos e algoritmos convencionalmente utilizados.
5. Considerações finais
O ensino do conteúdo de frações tem sido ao longo dos anos, uma repetição de mecanismos que pouco contribui para o desenvolvimento do raciocínio lógico matemático, e ainda hoje, em muitas escolas permanece o ensino “frontal”, no qualo professor explica os procedimentos e o aluno os repete nos exercícios. Assim, o que acontece no ensino de frações é um aprendizado apenas da linguagem de frações, sem a necessária compreensão do seu significado enquanto número.
Esta contestação foi a base do estudo que norteou o presente artigo questionando-se:
- “O Ensino de Matemática tem contribuído para o desenvolvimento da autonomia dos alunos?”
- “Que práticas privilegiam o desenvolvimento do raciocínio lógico?”; “O professor tem oportunizado a dialogicidade nas aulas?”
- “É possível aprender Matemática com significado?”
Estes questionamentos foram norteadores para a organização e o planejamento do Curso “As frações e seus diferentes significados” que teve como objetivo o aprofundamento conceitual e o aprimoramento de estratégias de ensino em uma perspectiva dialógica.
Ao se considerar a prática do professor como ponto de partida para o
Curso de formação de professores, valorizou-se a experiência profissional e se estabeleceu o elo entre a teoria e a prática, o que favoreceu o diálogo contribuindo para a compreensão de significados conceituais e procedimentais.
Na abordagem do conteúdo de frações, mais especificamente na ideia de fração como medida, fração unitária e equivalência de frações abordou-se um campo conceitual e não apenas um conceito isolado, destituindo de certa forma a linearidade com que normalmente os conteúdos de Matemática são trabalhados e possibilitando a reflexão dos professores sobre quais procedimentos e encaminhamentos são mais viáveis para a formação de alunos curiosos, participativos, pesquisadores e autônomos.
A inserção do estudo de textos nas Oficinas desencadeou nos professores o interesse pela leitura de livros e artigos que abordam conteúdos matemáticos e metodologias de ensino, constituindo-se em um recurso que pode contribuir na promoção de uma aprendizagem significativa para o aluno, e ao mesmo tempo para destituir a prática de ensino centrada em procedimentos mecânicos.
Assim, a abordagem do conteúdo de frações por meio do estudo de textos e da diversificação de procedimentos metodológicos na resolução das operações de adição e subtração de frações com denominadores diferentes no Curso “As frações e seus diferentes significados”, contribuiu para:
- Aprofundamento conceitual dos professores no que se refere ao conteúdo de frações provocando a inquietação que se transformou em estímulo para a busca de novos conhecimentos;
- Reconhecimento da importância do diálogo no processo de ensino e aprendizagem;
- Inserção da prática de leitura de textos referentes às estratégias de ensino, conteúdos e pesquisas na área de Matemática e Educação Matemática;
- Valorização por parte dos professores participantes da pesquisa de atividades práticas e da problematização de conteúdos como estratégias que possibilitam a compreensão de conceitos e algoritmos.
- Sensibilização dos professores para a escolha de práticas que proporcionem aos alunos o “pensar matemática”.
Portanto, aos Professores Cursistas foi oportunizado a ampliação/aprofundamento conceitual, a vivência de uma diversidade de procedimentos pedagógicos em uma perspectiva dialógica e concluiu-se que a contribuição maior refere-se à instrumentalização dos professores para escolhas pedagógicas.
6. Referências bibiliográficas
ALMEIDA, E. S. de (2010);“O jogo na teoria sociocultural - revendo os conceitos de Vygotsky”. Educação e Saúde - Psicopedagogia online. Disponível em: <www.psicopedagogia.com.br/artigos/artigo.asp?entrID=1194>. Acesso em: 20 set. 2010.
BAIER, T. (2005); O nexo “Geometria Fractal-produção da ciência contemporânea” tomado como núcleo do Currículo de Matemática do Ensino Básico”. 256f. Tese (Doutorado em Matemática) Universidade Estadual Paulista, IGCE – Rio Claro.
BRASIL, Ministério da Educação. Secretaria da Educação Fundamental.(2011);Parâmetros Curriculares Nacionais: matemática. 3.ed. Brasília: Secretaria da Educação.
DELIZOICOV, D.; ANGOTTI, J. A.; PERNAMBUCO, M. M. (2009); Ensino de ciências: fundamentos e métodos. 3 ed. São Paulo: Cortez.
FIORENTINI, D.; NACARATO, A. M.; PINTO, R. A.(1999);“Saberes da experiência docente em matemática e educação continuada.”Quadrante. São Paulo, 8, 33-60.
FREIRE, P. (1998); Pedagogia da autonomia. 6.ed. Rio de Janeiro: Paz e Terra.
LINS, R. C.; SILVA, H. (2008);Fascículo de Frações do Curso Pró-Letramento Matemática. Fascículo 4. In: BRASIL. Ministério da Educação. Pró-Letramento – Programa de Formação Continuada de Professores dos Anos/Séries Iniciais do Ensino Fundamental – Matemática–Frações.Brasília: MEC.
LORENZATO, S. (2008); Para aprender matemática. Campinas: Autores Associados.
LOTÉRIO, J. (2011); “A dialogicidade na educação: uma experiência com a Matemática.Revista da Unifebe, 198-210. Disponível em: <www.unifebe.edu.br/revistadaunifebe/2011/artigo033.pdf>. Acesso em: 10 mar. 2013.
MEDIANO, Z. D.(2008); A formação em serviço de professores através de oficinas pedagógicas. In: CANDAU, V. M. (Org.). Magistério – construção cotidiana. 6.ed. Petrópolis: Vozes, 91-109.
MOISES, R. P.; LIMA, L.C. (2010); “Como se criaram as unidades de medida”. Revista UOL Educação– Pedagogia e Comunicação. Medição - Ensino Fundamental, 3, Disponível em: <educacao.uol.com.br/.../medicao-como-se-criaram-as-unidades-de-medição>. Acesso em: 10 mar. 2013.
MOREIRA, M.A. (2004); A teoria dos campos conceituais de Vergnaud - o ensino de ciências e as investigações nessa área. Rio Grande do Sul: instituto de Física – UFRS.
NUNES, T.; et al.(2005);Educação Matemática: números e operações. São Paulo: Cortez.
_____.; BRYANT, P.(1997);Crianças fazendo matemática.Tradução Sandra Costa. Porto Alegre: Artmed.
PIRES, C. M. C. (2002);“Reflexões sobre os cursos de Licenciatura em Matemática, tomando comoreferência as orientações propostas nas Diretrizes Curriculares Nacionais para a formaçãode professores da Educação Básica.”Educação matemática em revista.Revista daSociedade Brasileira de Educação Matemática. São Paulo, 11, 44-56.
PONTE, J. P. (2010); “Explorar e Investigar em Matemática: Uma Actividade Fundamental no Ensino e na Aprendizagem”. Revista Iberoamerica de Educación Matemática, 21.
SANTOS, A. (2005);O conceito de fração em seus diferentes significados: um estudo diagnóstico junto a professores que atuam no Ensino Fundamental. Dissertação (Mestrado) - Pontifícia Universidade Católica. São Paulo.
SILVA, M. J. F. da. (2005);Investigando saberes dos professores do ensino fundamental com enfoque dos números fracionários para a 5ª série. 302f. Tese (Doutorado em Educação Matemática). Pontifícia Universidade Católica de São Paulo – PUC. São Paulo.
SILVA, D. S.(2007); Educação matemática – crítica e a perspectiva dialógica de Paulo Freire tecendo caminhos para a formação dos professores. In: ARAÚJO, J. de L. (org.) Educação matemática crítica – reflexões e diálogos. Belo Horizonte: Argvmentvm.
SILVEIRA, F. P.da. (2011); Conceito geral de fração. Artigo. Disponível em: <www.mat.ufrgs.br/~fundamentos1/perola2.htm>. Aceso em: 10 mar. 2013.
SKOVSMOSE,O. (2000). “Cenários para investigação”. Bolema, 14, 66 a 91.
VERGNAUD, G. (1994); Teoria dos campos conceituais. In: NASSER, L. (org.) Seminário Internacional de Educação Matemática. Anais. Rio de Janeiro, 1-26.
VYGOTSKY, L.(2008); Pensamento e linguagem. São Paulo: Martins Fontes.