1. Introdução
A utilização da Tecnologia da Informação e Comunicação (TIC), em especial do computador, para fins educacionais no cenário mundial ocorre em meados da década de 50 do século XX, a partir do momento que foi possível o armazenamento de informação no computador e capaz de programá-lo. Nesta época, a sua utilização reproduzia a tentativa de implementar a máquina de ensinar idealizada por Skinner (Valente, 1999).
A realidade brasileira em relação ao uso dessa tecnologia na educação apresentou certa insegurança sobre o seu resultado efetivo na sua utilização para aprendizagem e até mesmo na questão dos ambientes escolares com estes equipamentos (Valente, 2002). A necessidade de um olhar mais profundo sobre as vantagens pedagógicas são destacadas por Valente (2002, p.16), pois não era suficiente “enfatizar a melhoria do processo de transmissão de informação ou preparação do aluno para saber usar a informática”, mas que ao utilizá-la pudesse construir novos conhecimentos. Para que esse processo seja realizado com responsabilidade é preciso compreender o papel do computador e as vantagens pedagógicas com o seu uso.
Neste contexto, as duas ferramentas agregadas com os ambientes construcionista de aprendizagem para contribuir com a evolução bem como a propagação do conhecimento foram: o computador e os softwares educativos. Para tanto é necessário uma reflexão continuada das possibilidades e dos limites de uso do computador na educação.
Assim, esse artigo tem por objetivo apresentar a análise qualitativa em relação à modificação e à aquisição de novos conceitos, bem como verificar a contribuição do software Geogebra em uma atividade de intervenção com alunos do curso de Engenharia.
2. As possibilidades e os limites de uso do computador na educação
A evolução das pesquisas levaram a uma percepção do papel das tecnologias da informação e comunicação (TIC) para o ensino e a aprendizagem, além de que o computador pode auxiliar na construção de novos conhecimentos e na formação de um ciclo de aprendizagem (Valente, 2002).
No Brasil, no período de 1983 a 1994, em função dos recursos limitados para aquisição de computadores, o seu uso no contexto escolar foi reduzido aos softwares com a linguagem de programação Logo, jogos, tutoriais, entre outros.
Valente (2002, p. 19) destaca que: “é importante entender que a programação Logo possibilita muito mais do que a representação de ideias”. O aprendiz ao utilizar esta linguagem revê seus conceitos e pode tanto aprimorar como construir novos conhecimentos. A partir deste referencial que surge a noção de que a programação acontece em ciclos, auxiliando o processo de construção do conhecimento.
Segundo Valente:
O fato de o computador poder executar a sequência de comandos fornecida significa que ele está fazendo mais do que servir para representar ideias. Ele está sendo um elo importante no ciclo de ações: descrição-execução-reflexão-depuração, que pode favorecer o processo de construção de conhecimento (2002, p.19-20).
Neste ciclo de ações, Valente (2002, p. 23) aborda que a: “[...] interação com o computador apresenta características que são importantes na aprendizagem, que é entendida como um processo de construir novos conhecimentos”. A primeira etapa compreende como o aprendiz vai resolver um problema (descrição) depois deve inserir as estratégias no computador (execução). A máquina fará a ação que foi solicitada, mas não interage com o aprendiz, se houver algum erro simplesmente não conseguirá executar a ação pretendida. O aprendiz que deve analisar as ações executadas, independentemente dos resultados (reflexão), caso houver o erro precisa corrigi-lo (depuração).
Papert (1980) destaca “[...] a importância de enriquecer os ambientes de aprendizagem onde os sujeitos atuarão e serão capazes de construir os conceitos e ideias que impregnam esses ambientes”. Além disso, Valente (2002) aponta que a ideia de construção proposta por Piaget pode ser aprimorada, mas que o professor deve estar preparado para auxiliar os alunos, pois o mesmo pode exercer papel fundamental na formalização de conceitos que são convencionados historicamente.
Na representação dos conhecimentos explicitado no trabalho com o computador Valente (2002, p. 30-31) apresenta que: “[...] é o fato de ser possível identificar, do ponto de vista cognitivo, os conceitos e as estratégicas que o aprendiz utiliza para resolver um problema ou projeto”. Além do aspecto cognitivo, há o aspecto emocional no trabalho com o computar, este nem sempre é considerado.
A análise realizada por Valente (2002) na interação do aprendiz com o computador mostra que pode ser aplicada nas ações educacionais a distância, com o uso da Internet.
Para Valente (2002 apud Prado, 1996): “... essa formação está fundamentada na reflexão sobre a própria experiência que o aprendiz realiza no seu ambiente de trabalho”.
Valente (2002) considera que: “a prática que o aprendiz realiza no seu ambiente produz resultados que podem ser como objetos de reflexões. Estas reflexões podem gerar indagações e problemas, e o aprendiz pode não ter condições para resolvê-los”.
Neste momento o professor exerce papel de orientar o aluno para resolver seus problemas ou indagações e o aluno ao receber as orientações tenta aplicá-las ou pode surgir novas dúvidas que deverão novamente consultar o professor, gerando com isso um ciclo que auxilia o aluno na construção do conhecimento. A evolução deste ciclo pode gerar o espiral quando o aprendiz realiza as equilibrações em patamares majorantes, como proposto por Piaget.
Na busca de compreender como se dá a aprendizagem na relação aprendiz-computador, surgem: o computador para representar conhecimento, o ciclo de aprendizagem e o espiral de aprendizagem que busca superar as limitações que surgem com o uso do ciclo e é mais adequado para entender o processo de construção do conhecimento que surgem na relação aprendiz e as TIC e amplia que a aprendizagem não fica limitada ao aspecto cognitivo, mas podem tratar de aspectos como o social, o estético e o emocional, também (Valente, 2002).
Para Valente (1999, p. 105) “o computador deveria facilitar a educação e tornar as coisas mais fáceis para o estudante aprender, para o professor ensinar [...]”.
Em sua análise referente aos diferentes usos do computador Valente (1999, p. 105) concluiu que “os usos que são mais semelhantes às práticas pedagógicas tradicionais são os menos efetivos para promover a compreensão do que o aprendiz faz”.
A posição de Valente (1999) em relação ao uso do computador pelo aluno sem compreender o que está fazendo é mera informatização do processo pedagógico, mas se o mesmo auxiliar o aprendiz na construção do conhecimento e a compreender o que faz possibilitará “uma verdadeira revolução no processo de aprendizagem” que transformará a escola. Além de que o professor precisa estar preparado para desafiar, desequilibrar o aprendiz, pois o software por si não cria as situações para ele aprender e quando o professor aprimora suas habilidades de facilitador do processo de aprendizagem, ele deixa de ser um simples fornecedor da informação e instrutor do aluno e passa a ser um agente de aprendizagem.
O interesse na análise das potencialidades das TIC no ensino e na aprendizagem, para Coll, Mauri e Onrubia se desloca:
para o estudo empírico dos usos efetivos que professores e alunos fazem dessas tecnologias no transcurso das atividades de ensino e aprendizagem. Por outro lado, as possíveis melhoras de aprendizagem dos alunos são vinculadas à sua participação e envolvimento nessas atividades, nas quais a utilização das TIC é um aspecto importante, mas apenas um entre os muitos aspectos relevantes envolvidos (2010, p. 70).
As duas direções que a capacidade mediadora das TIC pode desenvolver nos processos de ensino e aprendizagem apresentadas por Coll, Mauri e Onrubia são:
em primeiro lugar, as TIC podem mediar as relações entre os participantes – especialmente estudantes, mas também os professores – e os conteúdos de aprendizagem. Em segundo lugar, as TIC podem mediar as interações e as trocas comunicacionais entre os participantes, seja entre professores e estudantes, seja entre os próprios estudantes (2010, p. 76).
As novas demandas da sociedade, para Gomes:
passam a exigir da escola a formação de cidadãos preparados para conviver na sociedade do conhecimento e da tecnologia. A reflexão que precisamos fazer é sobre como a humanidade tem se apropriado dessas inovações e se seus benefícios são extensíveis a todas as camadas da população (2002, p. 119).
O acesso às tecnologias, bem como a utilização dos recursos informáticos e comunicacionais com conotação educacional é restrita a uma pequena fração dos alunos, apesar de que a meta a ser atingida é possibilitar que esse acesso às tecnologias de informação e comunicação (TIC) seja igualitário a fim de contribuir para a melhoria da qualidade da educação (Gomes, 2002).
Em relação ao uso dos novos recursos das TIC, segundo Gomes (2002, p. 121) “[...] não deve ser encarada como mais uma novidade, mas como uma possibilidade para que alunos e professores assumam o papel de sujeitos críticos, criativos e construtores de seu próprio conhecimento”.
Neste cenário onde os ambiente de aprendizagem utilizam as TIC, o professor exerce um papel importante como mediador de todo o processo de ensino e aprendizagem (Gomes, 2002).
Gomes baseando em alguns autores relata que:
[...] a comunicação mediada por computadores está assentada na abordagem construtivista da aprendizagem, em que o conhecimento é uma construção realizada pelo sujeito e da qual resulta uma interpretação individual da experiência, legitimada pelos processos de interação social [...] (2002, p. 128).
Em relação a informática na educação, Carneiro relata que:
atualmente, pesquisadores e educadores estudam diferentes formas de utilização da tecnologia dentro de um ambiente de aprendizagem, investigando o processo de aprender e as características da cognição frente ao computador e a Internet, dando uma atenção especial ao uso do computador e suas possibilidades de utilização como ferramenta pedagógica e também como meio de entender de que forma o processo de aprendizagem se desenvolver a partir de tais estímulos (2002, p. 47).
Carneiro (2002, p. 53) afirma que “as questões a serem repensadas na escola, hoje, independem do uso efetivo da informática na sala de aula, mas sofrem grande influência quando há sua utilização”.
Em seus estudos Chaib (2002, p.49) tenta “entender o impacto da informática no conhecimento cotidiano e o seu significado social entre os professores”.
Em relação às mudanças tecnológicas, há estudos mostrando que tanto professores como alunos possuem representações ambivalentes sobre o computador, podendo expressar ou não otimismo ou pessimismo (König, 1997; Hugo, 1997, apud Chaid, 2002). Os mesmos estudos apresentam que nesta ambivalência o computador tem três formas de representação simbólica, sendo visto como: “uma ferramenta que inflige mudanças” ou “um instrumento usado para aumentar o conhecimento” ou “um difícil e confuso dispositivo, quando é usado para se tomar decisões sobre o ensino” (König, 1997; Hugo, 1997, apud Chaid 2002, p. 50).
3. Material e Métodos
No intuito de analisar qualitativamente a modificação e aquisição de novos conhecimentos, bem como a contribuição do uso do computador, em especial o software Geogebra em sala de aula optou-se por realizar uma atividade de intervenção com trinta e nove alunos do primeiro período do curso de Engenharia de Controle e Automação, da Universidade Tecnológica Federal do Paraná, Câmpus Cornélio Procópio. A amostra foi definida tendo em vista que se trata do ambiente natural de trabalho de um dos autores desta pesquisa e, também, pelo programa curricular do curso quando da intervenção.
Para desenvolvimento da atividade formaram-se grupos de três alunos, onde os mesmos deveriam desenvolver o conceito de área sob uma curva (soma de Riemann e integral definida). Esta análise dos grupos teve como referência a variação dos resultados da soma das áreas obtidas pela aproximação de uma região por retângulos inferiores e por retângulos superiores e em seguida aplicar o limite das áreas desses retângulos (inferiores e superiores) à medida que variasse o número de partições e consequentemente o número de retângulos em um dado intervalo dessa curva. O software Geogebra de geometria dinâmica foi escolhido para auxiliar os alunos em sua análise, em função de ser aberto e permitir a visualização gráfica e a descrição de comandos. Ao final da análise deveriam registrar as suas percepções comparando os resultados dos limites das áreas desses retângulos (inferiores e superiores) com o valor da integral, além de por meio da escrita, registrar suas as percepções.
Para a análise dos registros foram escolhidos ao acaso quatro dentre os treze grupos que realizaram a atividade. E, para a análise dos dados coletados foi utilizada a análise de conteúdo por ser um instrumento de análise interpretativa que possibilita uma construção que parte da realidade concreta da situação estudada. Para Moraes (1999, p. 7) a “análise de conteúdo constitui uma metodologia de pesquisa usada para descrever e interpretar o conteúdo de toda classe de documentos e textos”.
Para tanto foi apresentado aos alunos os aspectos definidores do conceito de área sob uma curva que segundo Anton, Bivens e Davis (2007, p. 388): “se uma função é contínua em um intervalo [a,b], então é integrável em [a,b] e a área líquida com sinal A entre o gráfico de f e o intervalo [a,b] é A= ”, ou seja, os aspectos definidores são a função estudada no intervalo fechado ( )e a integral definida. Em relação aos aspectos característicos são: número de partições do intervalo, a área dos retângulos inferiores e área dos retângulos superiores.
Para verificar as alterações na área sob a curva em relação ao eixo x em um dado intervalo fechado, os grupos usaram o software Geogebra a fim de realizarem a atividade conforme o ciclo de ações definido por Valente (2002). As etapas do ciclo de ações foram as seguintes: (a) descrição (os comandos para execução do software:Função[ <Função>, <Valor de x Inicial>, <Valor de x Final> ]. Na atividade o comando digitado foi Função[-x^2+4 x, 0, 4];SomaDeRiemannInferior[ <Função>, <Valor de x Inicial>, <Valor de x Final>, <Número de Retângulos>]. Na atividade o comando digitado foi o seguinte: SomaDeRiemannInferior[f, 0, 4, n]; SomaDeRiemannSuperior[ <Função>, <Valor de x Inicial>, <Valor de x Final>, <Número de Retângulos>]. Na atividade o comando digitado foi o seguinte: SomaDeRiemannSuperior[f, 0, 4, n] e Integral[ <Função>, <Valor de x Inicial>, <Valor de x Final>]. Na atividade o comando digitado foi o seguinte: Integral[f, 0, 4]; (b) execução: plotagem do gráfico no software disponibilizando na tela do computador os resultados obtidos para as somas de Riemann tanto inferior como superior e para a integral definida; (c) reflexão: análise da área sob a curva por retângulos (inferiores e superiores) em relação ao intervalo dado no eixo x e ao número de partições e o resultado obtido com a integral definida; (d) depuração: verificar a necessidade de refazer o ciclo depois da análise comparativa dos resultados obtidos por: áreas dos retângulos superiores e áreas dos retângulos inferiores e pela integral definida.
Segundo Valente (2002) ao realizar atividade com o computador em sala de aula o aluno tem a possibilidade de abstrair e até chegar ao nível abstração reflexionante o que permite que ele adquira novos conceitos e até mesmo modifique conceitos anteriores. E é justamente o registro de tal abstração que permitirá analisar a fim de identificar a mudança e até mesmo a aquisição de novos conceitos.
Com base na análise de conteúdo e mediante os aspectos característicos do cálculo de área sob a curva criou-se como categorias: a soma das áreas inferiores, a soma de áreas superiores e a integral definida. Como unidades foram definidas as etapas do ciclo de ação, ou seja, descrição, execução, reflexão e depuração, conforme Figura 1.
A partir da definição das categorias e unidades de análise verificou se as atividades realizadas pelos quatro grupos escolhidos ao acaso e possibilitou perceber que todos efetuaram as atividades de acordo com o ciclo de ações proposto por Valente (2002), mas houve equipe que não apresentou registro referente a determinadas etapas do ciclo. Alguns grupos não tiveram necessidade de realizar a depuração, pois chegaram conseguiram consolidar o conceito desejado sem a necessidade de repetir o ciclo.
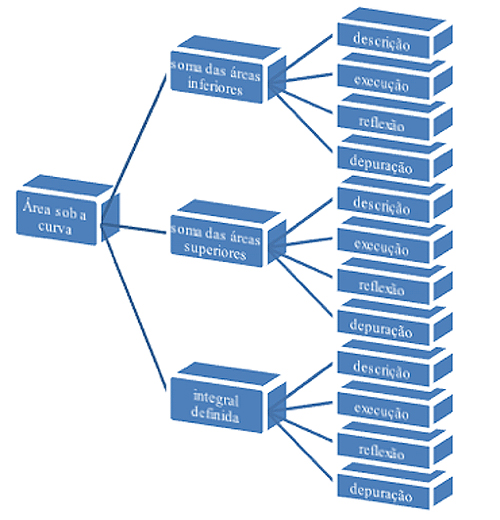
Figura 1 – Categorias e unidades de análise
Fonte: Autores
Dessa forma, a análise foi realizada com base nas percepções dos grupos, resultado da abstração reflexionante, decorrentes da variação do valor da área sob a curva em função da alteração do número de partições no intervalo definido e a comparação com o valor da integral.
A análise ocorreu na tentativa de identificar nos textos produzidos pelos grupos de alunos as categorias corretas e também verificar os motivos dos erros encontrados.
4. Resultados e Discussão
Nos Quadros 1, 2 e 3 apresentam-se de acordo com a definição da amostra e das categorias de análise, a transcrição dos registros feitos pelos grupos e comparando-as com as respostas corretas com base nos princípios de cálculo de área sob uma curva (soma de Riemann e integral definida). Em seguida registrou-se a análise dos pesquisadores no qual buscou compreender o que levou cada grupo a realizar determinados registros. Nos Quadros a seguir apresentam-se cada categoria e os registros, bem como os textos criados para análise das atividades e suas respectivas avaliações (correto, parcialmente correto ou incorreto).
A primeira análise deu-se da categoria de soma das áreas dos retângulos inferiores seguida da soma das áreas dos retângulos superiores e integral definida.
Categoria: Soma das áreas dos retângulos inferiores Descrição: A área sob a curva da função f(x)= -x^2+4.x no intervalo delimitado pelas retas x=0 e x=4 com partições variando de 1 a 100 utilizando soma de Riemann por retângulos aproximantes inferiores. Registro correto: O valor da área sob a curva obtida pela soma das áreas dos retângulos inferiores, conforme for aumentado o número de partições se aproxima do valor da integral definida no mesmo intervalo. Neste caso a variação da área será de 0u.a. a 10,51u.a. aproximadamente para a variação do número de partições de 1 a 100. |
||
Grupo |
Registro do grupo |
Avaliação do registro |
G1 |
A área da soma inferior fica abaixo do ponto máximo (2,4), possuindo uma área inicial para n=1(número de partições), no eixo x entre 0 e 4, e no eixo y entre 0 e 4, ou seja, um quadrado de 4x4, assim, sua área inicial será de 0 u. Aumentando o valor de n, a Si irá aumentar cada vez mais, aumentando consequentemente a área inferior. A área da soma inferior será cada vez mais próxima do valor real, pois a área “perdida” entre a parábola e os retângulos vai se tornando menor, se aproximando do valor zero. |
Correto |
G2 |
Variando o número n de retângulos (positivamente), obtemos um valor cada vez mais próximo da integral. Se diminuirmos o número n de retângulos o valor da soma inferior também diminui portanto a Soma Inferior é proporcional ao número n de retângulos. |
Correto |
G3 |
Analisando o valor da Soma Inferior com o valor atribuído a n, pudemos verificar que conforme o n aumenta, a Soma Inferior também aumenta. |
Parcialmente correto |
G4 |
Conforme aumentamos o número n de partições, observamos que os valores da soma inferior ficam maiores, aproximando-se do valor encontrado através do cálculo da integral. |
Correto |
G1, G2 e G4 – o registro destes grupos estão corretos. / G3– o registro deste grupo está parcialmente correto tendo em vista que não fez nenhuma relação com o objetivo da intervenção que foi comparar os resultados das somas das áreas dos retângulos inferiores com a integral definida no mesmo intervalo. |
||
Quadro 1 – Análise da categoria Soma das áreas dos retângulos inferiores
Fonte: Autores
Com base nessa categoria foi possível observar que todos os grupos deixaram implícito que utilizaram os resultados obtidos com o auxílio do software Geogebra para apresentar suas conclusões e que pode ser falta de atenção por parte dos membros dos grupos ou falta de clareza na exposição dos objetivos da intervenção por parte do professor que levaram alguns dos grupos apresentarem restritos da análise dos resultados da soma das áreas dos retângulos inferiores não associando com a integral definida no mesmo intervalo, sendo com isso considerado o resultado desta etapa da atividade como parcialmente correto.
Para continuidade da análise apresenta-se o Quadro 2 envolvendo a categoria da Soma das áreas dos retângulos superiores.
Categoria: Soma das áreas dos retângulos superiores Descrição: A área sob a curva da função f(x)= -x^2+4.x no intervalo delimitado pelas retas x=0 e x=4 com partições variando de 1 a 100 utilizando soma de Riemann por retângulos aproximantes superiores. Registro correto: O valor da área sob a curva obtida pela soma das áreas dos retângulos superiores, conforme for aumentado o número de partições se aproxima do valor da integral definida no mesmo intervalo. Neste caso avaliação da área será de 16 u.a. a 10,83 u.a. aproximadamente para a variação do número de partições de 1 a 100. |
||
Grupo |
Registro do grupo |
Avaliação do registro |
G1 |
A área da soma superior fica acima do ponto máximo (2,4), possuindo uma área inicial para n=1(número de partições), no eixo x entre 0 e 4, e no eixo y entre 0 e 4, ou seja, um quadrado de 4x4, assim, sua área inicial será de 16 u. Aumentando o valor de n, a Ss irá diminuir, diminuindo consequentemente a área superior. A área da soma superior será cada vez mais próxima do valor real, pois a área sobre a parábola e os retângulos vai se tornando menor, se aproximando do valor zero. |
Correto |
G2 |
Quanto maior o número n de retângulos, mais próximo o valor se aproxima da integral. Quanto maior o número n de retângulos, menor o valor da soma superior, a Soma Superior é inversamente proporcional ao número n de retângulos. |
Correto |
G3 |
Para a Soma Superior, o comportamento é ao contrário, já que seu valor diminui conforme n aumenta. |
Parcialmente correto |
G4 |
Quanto à soma superior, temos o processo inverso. Num número pequeno de partições, temos um valor superior ao valor da integral, mas conforme aumentamos n, os valores vão diminuindo, aproximando-se do valor da integral. Analisando ambas simultaneamente, notamos comportamentos inversos conforme a variação de partições. Isto acontece como um processo de linearização, onde a soma superior (uma aproximação feita com valores superiores ao valor real da área) e a soma inferior (aproximação feita com valores inferiores ao valor real da área) tendem a um valor comum, que é o próprio valor da integral que calculamos acima. |
Correto |
G1, G2 e G4 – o registro destes grupos estão corretos. / G3– o registro deste grupo está parcialmente correto tendo em vista que não fez nenhuma relação com o objetivo da intervenção que foi comparar os resultados das somas das áreas dos retângulos inferiores com a integral definida no mesmo intervalo. |
||
Quadro 2 – Análise da categoria Soma das áreas dos retângulos superiores
Fonte: Autores
Em relação a categoria Soma das áreas dos retângulos superiores pode-se perceber que em função da similaridade de comportamento desta com a categoria Soma das áreas dos retângulos inferiores os grupos replicaram a mesma análise, com isso obtiveram os mesmos resultados.
A seguir apresenta-se a análise do Quadro 3 envolvendo a categoria Integral definida
Categoria: Integral definida Descrição: A área sob a curva da função f(x)= -x^2+4.x no intervalo delimitado pelas retas x=0 e x=4 utilizando integral definida. Registro correto: que a área é de 10,67u.a. |
||
Grupo |
Registro do grupo |
Avaliação do registro |
G1 |
10,667 |
correto |
G2 |
Os valores crescem de -10,37 a 0 |
incorreto |
G3 |
10,67 |
correto |
G4 |
10,67 |
correto |
G1, G2, G4 – os registros destes grupos estão correto. / G3 - o registro deste grupo está incorreto tendo em vista que não os valores apresentados em seus registros não condizem com a integral definida nem com a área, pois são resultados negativos. |
||
Quadro 3 – Análise da categoria Integral definida
Fonte: Autores
Em relação a esta categoria Integral definida vale destacar o fato do grupo G2 não se incomodar com o resultado negativo da integral da função dada no intervalo estabelecido, tendo em vista que pode ser uma desatenção ou que os membros dos dois grupos não compreenderam o conceito de área sob a curva e que a área é um valor absoluto, ou seja, não pode ser negativa.
Para representar de forma mais sintética elaborou-se o Quadro 4 com as frequências das avaliações realizadas de cada registro.
|
Soma das áreas dos retângulos inferiores |
Soma das áreas dos retângulos superiores |
Integral |
||||||
Grupo |
C |
PC |
I |
C |
PC |
I |
C |
PC |
I |
G1 |
X |
|
|
X |
|
|
X |
|
|
G2 |
X |
|
|
X |
|
|
|
|
X |
G3 |
|
X |
|
|
X |
|
X |
|
|
G4 |
X |
|
|
X |
|
|
X |
|
|
Total |
75% |
25% |
0% |
75% |
25% |
0% |
75% |
0% |
25% |
Quadro 4 – Frequência da avaliação dos registros
C = correta, PC = parcialmente correta e I = incorreta
Fonte: Autores
Os pesquisadores apresentam, a seguir, a sua visão em relação às análises realizadas diante dos registros dos grupos. Essa etapa equivale a um metatexto.
Nas categorias Soma das áreas dos retângulos inferiores e Soma das áreas dos retângulos superiores apresentaram os mesmos resultados entre as equipes analisadas, sendo 75% de registros corretos e 25% de registros parcialmente corretos, tendo em vista que há um comportamento similar entre estas categorias e o grupo que apresentou o resultado parcialmente correto foi em função de não relacionar a Soma das áreas dos retângulos tanto inferiores como Superiores com a Integral definida.
Na categoria Integral definida o resultado esteve nos extremos, correto e incorreto, sendo 75% de registros corretos e 25% de registros incorretos. No caso do registro incorreto ocorreu que o grupo não tiveram a percepção ou não compreenderam o conceito de área até o momento, pois não se incomodou com o resultado negativo para o valor da Integral Definida obtido com o auxílio do Software Geogebra. Apesar deste resultado pode-se perceber que o mesmo compreendeu a relação entre a Soma das áreas dos retângulos tanto inferiores como Superiores com a Integral Definida.
É possível destacar ainda que a utilização de linguagem apresentada nos registros dos grupos estão próximas da utilizada na matemática, este fato pode ter relação com a familiaridade que foi criada com a atualização deste recurso para auxiliar a aprendizagem, proporcionado o desenvolvimento, a interpretação e a compreensão de atividades matemáticas.
Vale destacar que esta pesquisa desenvolvida por intermédio de uma intervenção teve o intuito de utilizar um software que possibilitasse auxiliar na visualização gráfica da função estabelecida, fornecer os resultados em cada categoria e assim compreender a relação entre a Soma das áreas dos retângulos tanto inferiores como Superiores com a Integral Definida. Esta compreensão fica evidente no registro de um dos grupos: “Com o auxílio das tabelas que fornecem os dados retirados dos plotamentos da função feitos para cada partição (n), pode-se perceber que o aumento da divisão de partições reflete na precisão da medição da área varrida pelo gráfico da função f, visto que os valores das medidas das áreas aproximam-se do valor exato da área, 10,67, que já sabemos, visto que o comando “Integral[]” do programa Geogebra nos fornece essa informação”.
5. Considerações finais
Os estudos realizados com o intuito de verificar as possibilidades de uso do computador em contexto de ensino apresentam que o mesmo pode auxiliar na resolução de problemas facilitando que o aluno entenda conceitos complexos e mais abstratos e ao utilizar um programa o aluno pode rever seus conceitos e assim pode tanto aprimorar como construir novos conhecimentos.
O ciclo de ações proposto por Valente: descrição-execução-reflexão-depuração, tem o intuito de verificar se os objetivos traçados pelo aluno para resolver um determinado problema utilizando os recursos disponíveis no computador foi atingido e assim favorecer o processo de construção do conhecimento.
Outro fator importante é que o interesse e o envolvimento do aluno é indispensável para melhorar sua aprendizagem e o uso das TIC podem mediar as interações e as trocas comunicacionais entre professores e estudantes, ou entre os próprios estudantes, e também entre os professores – e os conteúdos de aprendizagem. Assim, tanto alunos e como professores podem assumir o papel de sujeitos críticos, criativos e construtores de seu próprio conhecimento.
A Matemática, em particular, apresenta-se na formação do aluno como uma das áreas cuja operacionalização do raciocínio é realizada por um código de linguagem própria e não há necessidade, na maioria das vezes, de expressar a sua compreensão. Em função disso, os responsáveis desta pesquisa levaram em consideração os aspectos definidores e característicos da área sob uma curva.
Para tanto, utilizando-se do software Geogebra e o ciclo de ações definido por Valente procurou-se estruturar a proposta da atividade para os alunos. A partir dos resultados apresentados pelos grupos optou-se pela análise de conteúdo apresentada por Moraes que proporcionou criar as categorias e unidades de registros, conforme Figura 1.
A percepção dos pesquisadores em relação aos registros dos grupos evidencia que, após um semestre de intervenções com a utilização das tecnologias em situações de aprendizagens geraram uma certa familiaridade com o Software Geogebra e os auxiliaram para expressar por meio da língua portuguesa: o desenvolvimento, a interpretação e a compreensão das atividades matemáticas propostas e assim proporcionou que a maioria destes alunos pudessem formar o conceito de área sob um curva.
Referências bibliográficas
Anton, H.; BivensS, I.; Davis, S. Cálculo. 8.ed. v. 1.Porto Alegre: Bookman, 2007.
Carneiro, R. Informática na educação: representações sociais do cotidiano. São Paulo: Cortez, 2002.
Chaib, M. Frankstein na sala de aula: as representações sociais docentes sobre informática. Nuances, n. 8, set. 2002, p.47-64.
Coll, C.; Mauri, T.; Onrubia, J. A incorporação das tecnologias de informação e da comunicação na educação: do projeto técnico-pedagógico às práticas de uso. In: Coll, C.; Monereo, C. (org.). Psicologia da Educação Virtual: aprender e ensinar com as Tecnologias da Informação e da Comunicação. Porto Alegre: Artmed, 2010. p. 66-93.
Gomes, N. G. Computador na escola: novas tecnologias e inovações educacionais. In: Belloni, M. L (Org.). A formação na sociedade do espetáculo. São Paulo: Loyola, 2002. p. 119-134.
Moraes, R. Análise de conteúdo. Revista Educação, mar. 1999. v. 22, n. 37, p. 7-32.
Papert, S. Computadores e Culturas do Computador. In: Logo: computadores e educação. São Paulo: Brasiliense,1985. p. 35-57
Valente, J. A. O computador na sociedade do conhecimento. Campinas: UNICAMP/NIED, 1999.
_____. A espiral da aprendizagem e as tecnologias de informação e comunicação: repensando conceitos. In: Joly, M. C. R. A. (org.) A Tecnologia no Ensino: implicações para a aprendizagem. São Paulo: Casa do Psicólogo, 2002. p. 15-37.