1. Introdução
As mudanças ocorridas na sociedade têm apresentado fortes influências e características da pós-modernidade. A alteração repentina de atitude, de humor, de desejos, dos costumes das pessoas entre outras tem sido as maiores representações da consequência do mundo pós-moderno. Mas afinal o que se entende por pós-modernismo? Pode-se dizer que é um movimento social que surge como uma forma cultual de dominação e que traz consigo novas maneiras de socialização, de pensar e de agir.
A presença de objetos tecnológicos como telefones celulares, tablets, notebook, entre outros faz com que a escola busque se adaptar aos indivíduos contemporâneos e para tentar cumprir com sua função ela tem a necessidade de aprender a utilizar estes recursos tecnológicos para atrair a atenção dos alunos. Acredita-se que toda essa presença dos objetos tecnológicos tem causado desestabilidade na escola e em grande velocidade fazendo com que ela não tenha condições de se adaptar a todas essas características dessa nova sociedade.
(...) cada vez mais crianças, constituídas por novas e variadas práticas culturais, adentram nossas escolas, causando inquietações, desestabilizando e incomodando, porque, de certa forma, já não é mais possível classificá-las e enquadrá-las em uma cartografia. Sem essa garantia de ordem e estabilidade, por longo tempo assegurada pelos enquadramentos pedagógicos modernos, educadores dos tempos pós-modernos estão inseguros, sem rumo, confusos, quase imobilizados. (Momo e Costa, 2010, p. 988).
Mesmo com toda a tentativa de inclusão dos recursos tecnológicos na sala aula os professores sentem que há dificuldade de prender a atenção dos alunos, pois não se trata apenas no uso destes recursos e sim de como fazer com que os alunos se interessem pelos conhecimentos escolares.
O que se pode perceber é que a escola tem sofrido perturbações e mesmo com toda iniciativa dos profissionais da educação tem sido quase que impossível fazer com que os alunos tenham interesse em aprender conteúdos disciplinares e dessa forma construam seu próprio conhecimento. Pode-se se dizer que a escola foi invadida por
Seres estranhos, ameaçadores e incompreendidos nos olham nos pátios, corredores e salas de aula. A infância como fase da inocência, da dependência, da insegurança e da ignorância dos segredos do mundo e da vida parece que está desaparecendo rapidamente. No lugar dela instalam-se as infâncias dos tempos pós-modernos, insondáveis, múltiplas, instáveis, paradoxais, selvagens, incontroláveis, enigmáticas (Momo e Costa, 2010, p. 988-989).
É inegável que o espaço escolar necessita de mudanças e que estas exigem além de políticas públicas, capacitação de professores na formação inicial e continuada para utilização dos recursos tecnológicos bem como a aquisição de equipamentos de tecnologia. Dessa forma, faz-se necessário adequar a sala de aula à realidade dos alunos. É importante que a escola se torne um ambiente atrativo para o ensino de conteúdos disciplinares e a construção de conhecimento, e não somente um local para seus alunos exibirem seus objetos tecnológicos.
2. O computador e seu uso
A sociedade necessita de indivíduos criativos e com a capacidade para criticar de modo construtivo, pensar, aprender sobre aprender, trabalhar em grupo e conhecer seus próprios potenciais. Isso requer um indivíduo que está atento às mudanças que acontecem em nossa realidade e que tenha a capacidade de constantemente melhorar e reorganizar suas ideias e ações. Tal necessidade implica na transformação das escolas de hoje. Essa transformação é muito mais profunda do que simplesmente instalar o computador como um novo recurso educacional, pois aprender um determinado assunto deve ser o produto de um processo de construção de conhecimento realizado pelo aprendiz e por intermédio do desenvolvimento de projetos que usam o computador como uma fonte de informação ou recurso para resolver problemas significativos para o aprendiz (Valente, 1999).
O computador pode ser um importante recurso no processo de construção de conhecimento pelos alunos. Ao questionarmos “por que usar computadores na educação?”, a resposta mais provável é o fato de estarmos interessados em explorar as características dos computadores que contribuem para o processo de conceituação ou construção do conhecimento. Ele pode refletir sobre os resultados de suas ações e ideias, e esta reflexão é o mecanismo pelo qual o aprendiz se torna consciente de seu conhecimento e, assim, pode transformar seus esquemas mentais em operações e noções mais complexas. A grande maioria dos educadores acredita que o computador motiva o aluno, que é a ferramenta da atualidade ou que facilita o aprendizado. No entanto, os diferentes usos do computador na sala de aula levaram à conclusão de que os usos que são mais semelhantes à práticas pedagógicas tradicionais são os menos efetivos para promover a compreensão do que o aprendiz faz (Valente, 1999).
Assim, o uso do computador em sala de aula tem modificado a ideia de ser um simples instrumento no processo pedagógico tornando-se um importante auxiliador no processo de ensino e de aprendizagem e na construção de conhecimentos pelo aprendiz, permitindo assim repensar sobre a aprendizagem de conceitos que estão presentes na interação do aprendiz com recurso tecnológico.
Diante desses aspectos, verificou-se a aprendizagem do conceito de função afim, seus parâmetros e o comportamento gráfico, em alunos ingressantes do curso de licenciatura em Matemática por meio da utilização do software Geogebra.
3. Descrevendo o estudo
Este trabalho foi realizado com quatorze acadêmicos do primeiro ano de um curso de licenciatura em Matemática de uma Instituição de Ensino Superior, pública, do interior do Paraná, na disciplina de Função. Objetivou-se, por meio de uma atividade, verificar a aprendizagem do conceito de função afim, seus parâmetros e o comportamento gráfico por meio da utilização do software Geogebra. Pois, acredita-se que
O oposto à matemática pronta é a matemática em status nascente. Isto é o que Sócrates ensinou. Hoje, desejamos que isso seja um começo real ao invés de ser estilizado; o educando deve, por ele mesmo, reinventar matemáticas... O processo de aprendizagem tem que incluir fases de invenções dirigidas, isto é, de invenções não no sentido objetivo, mas no senso subjetivo, visto da perspectiva do estudante (Freudenthal, 1973, apud Steinbring, 2005, p.15).
Para a realização da atividade, dividiu-se os alunos da turma em duplas, na qual se buscou compreender de que forma os acadêmicos entendem o uso de recurso tecnológico na construção do conceito de função. Assim, inicialmente, foi solicitado que fizessem a definição da função afim e o comportamento gráfico da mesma em relação aos seus parâmetros bem como o registro da contribuição do uso do software Geogebra. Para isto, a atividade foi desenvolvida de modo que os acadêmicos a refletissem sobre o uso de recursos tecnológicos na construção do conhecimento.
Então, foi solicitado aos acadêmicos que definissem a função afim até mesmo pelo fato de ser um conceito prévio advindo da Educação Básica e também pela sua presença na licenciatura em Matemática. Após, discutiu-se sobre os aspetos definidores da função afim (o conjunto domínio e a função (x, ax+b)) e os aspectos característicos (dependentes dos parâmetros a e b) que são imagem e comportamento gráfico da função. Em seguida solicitou-se que realizassem a construção gráfica da função afim e registrassem de modo escrito o comportamento gráfico em relação aos seus parâmetros em cada um dos quatro momentos conforme indicado no Quadro 1:
Quadro 1 – Situações para análise do comportamento gráfico da função afim |
Posterior a essa atividade, solicitou-se que os acadêmicos descrevessem de que forma o uso do software Geogebra pode contribuir na aprendizagem do conceito de função afim, acredita-se que
Todo conhecimento matemático, seja ele científico ou escolar, necessita do contexto de referência, e, neste sentido, todo conhecimento é um contexto específico. Sobre esta base, a diferença entre matemática científica e escolar encontra-se nos diferentes tipos de contextos de referências usados nestes diferentes contextos de desenvolvimentos sociais. Uma diferença importante diz respeito ao contexto de referência na matemática escolar, a qual deve ser ajustada para a necessidade da aprendizagem e do desenvolvimento cognitivo dos estudantes (Steinbring, 2005, p.13).
As duplas realizaram várias discussões acerca do conceito envolvido na atividade. Durante a realização da atividade buscou-se verificar o conceito de função afim pelos alunos além de apresentar uma atividade que possibilita a construção de conhecimento por meio da utilização do software Geogebra em sala de aula. Assim, ao final da atividade foram recolhidos os registros escritos para posterior análise.
A pesquisa caracterizou-se como qualitativa, pois o pesquisador buscou coletar dados e analisá-los de modo a atingir o objetivo de verificar a aprendizagem do conceito de função afim em acadêmicos do no curso de licenciatura em Matemática. Pois, de acordo com Bogdan e Biklen (1994), a pesquisa qualitativa pode ser entendida como a tentativa de compreensão de significados e características de situações apresentadas por entrevistados ou pesquisados, para se aprofundar nos fenômenos, levando em conta a sua complexidade e particularidades, de maneira a não almejar generalizações e sim a compreensão das singularidades.
Por se tratar de sete duplas, decidiu-se escolher quatro duplas que realizaram a atividade. As duplas foram numeradas de um a sete, sendo escolhidas ao acaso as quatro duplas (D1, D2, D3, D4) que foram analisadas neste trabalho.
Para a análise dos registros produzidos pelos acadêmicos na atividade realizada optou-se pela análise de conteúdo, pois é considerado um instrumento de análise interpretativa que possibilita uma compreensão que parte da realidade concreta da situação estudada. Para Moraes (1999, p. 7) a “análise de conteúdo constitui uma metodologia de pesquisa usada para descrever e interpretar o conteúdo de toda classe de documentos e textos” e pode ser considerado um instrumento,
um guia prático para a ação, sempre renovada em função dos problemas cada vez mais diversificados que se propõe a investigar. Pode-se considerá-la como único instrumento, mas marcado por uma grande variedade de formas e adaptável a um campo de aplicação muito vasto, qual seja a comunicação (Moraes, 1999, p. 7).
A metodologia de análise de conteúdo constitui um conjunto de procedimentos de análise das comunicações, orais ou escritas, cujo objetivo é encontrar indicadores, qualitativos ou quantitativos, que possibilitem inferir (deduzir de forma lógica) sobre conhecimentos relacionados às mensagens analisadas. Assim, a análise de conteúdo é indicada quando o pesquisador pretende manipular as mensagens para inferir “conhecimentos sobre o emissor da mensagem ou sobre o seu meio” (Bardin, 2009, p. 34).
Desse modo, sendo a análise de conteúdo um instrumento que pode ser adaptado a uma variedade de pesquisa, coube ao pesquisador determinar uma maneira de fazer o uso desta metodologia neste trabalho de modo a atingir o objetivo anteriormente definido.
4. Estrutura da análise
Utilizando como base a análise de conteúdo e mediante os aspectos característicos da função afim, definiu-se como categorias a priori os quatro momentos apresentados anteriormente no Quadro 1. Tal escolha de se deu em concordância com o que diz Bardin (1999) a respeito do processo de categorização, pois este “tem como objectivo (da mesma maneira que a análise documental) fornecer, por condensação, uma representação simplificada dos dados brutos” (Bardin, 1999, p. 112) e também pelo conjunto de “boas características” que as categorias devem possuir:
- a exclusão mútua: esta condição estipula que cada elemento não pode existir em mais de uma divisão. As categorias deveriam ser construídas de tal maneira que um elemento não pudesse ter dois ou vários aspectos susceptíveis de fazerem com que fossem classificados em duas ou mais categorias;
- a homogeneidade: o princípio da exclusão mútua depende da homogeneidade das categorias. Um único princípio de classificação deve governar a sua organização;
- a pertinência: uma categoria é considerada pertinente quando está adaptada ao material de análise escolhido, e quando pertence ao quadro teórico definido;
- a objectividade e a fidelidade: estes princípios, tidos como muito importantes no início da história da análise de conteúdo, continuam a ser válidos. As diferentes partes de um mesmo material, ao qual se aplica a mesma grelha categorial, devem ser codificadas da mesma maneira, mesmo quando submetidas a várias análises;
- a produtividade: adicionaremos às condições geralmente invocadas uma qualidade muito pragmática. Um conjunto de categorias é produtivo se fornece resultados férteis: férteis em índices de inferências, em hipóteses novas e em dados exactos. (Bardin, 1999, p. 113-114).
Para a definição das unidades de registro baseou-se nos critérios de correção e avaliação apresentado por Buriasco, Cyrino e Soares (2004) que possibilitam corrigir e registrar a produção discente na resolução de questões abertas. A adoção de tal método se dá tendo em vista que
as respostas dos alunos não devem ser codificadas apenas como certas ou erradas, e sim, separadas inicialmente em três blocos - “responde adequadamente a questão”, “responde parcialmente a questão” e “não responde a questão” – e classificadas como - “crédito completo”, “crédito parcial” e “nenhum crédito”, respectivamente (Buriasco, Cyrino e Soares, 2004, p. 5).
As autoras consideram que este método de correção possibilita ao professor verificar a compreensão do aluno em relação ao que foi solicitado na atividade de modo a identificar o que ele já conhece ou está em busca de aprender, pois “se a resposta dada a uma questão está incorreta, necessariamente a produção do aluno deve ser examinada para considerar possíveis créditos parciais” (Buriasco, Cyrino e Soares, 2004, p. 6). Assim, definiu-se a estrutura de análise, onde as categorias são os momentos apresentados no Quadro 1 e as unidades são os critérios definidos por Buriasco, Cyrino e Soares (2004).
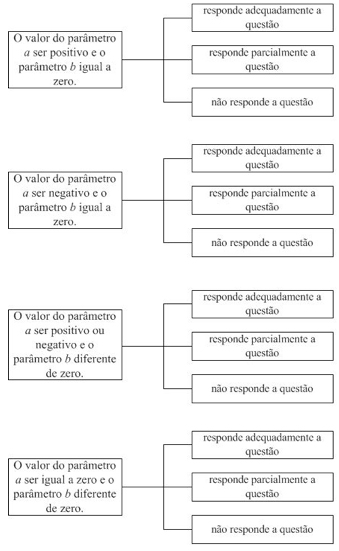
Fig. 1 – Categorias e unidades de análise
Fonte: os autores (2013)
Após escolha da estrutura acima se iniciou a análise dos registros apresentados e a avaliação realizada baseados na análise de conteúdo no qual são apresentados adiante.
5. Análise dos registros
Nos Quadros 2, 3, 4 e 5 apresenta-se, de acordo com a definição da amostra e das categorias de análise, a transcrição dos registros realizados pelas duplas e a comparação com as respostas corretas de acordo com a definição e o comportamento gráfico da função afim. Também se registrou um meta texto no qual se buscou compreender a aprendizagem do conteúdo pelos alunos. Nos Quadros a seguir apresenta-se cada categoria, os registros e os textos criados para a análise das atividades e suas respectivas avaliações.
A primeira análise deu-se da categoria: O valor do parâmetro a ser positivo e o parâmetro b igual a zero, conforme Quadro 2.
Categoria: O valor do parâmetro a ser positivo e o parâmetro b igual a zero. |
||
Dupla |
Registro da dupla |
Avaliação |
D1 |
A reta será crescente e passará pelo o ponto de origem e a reta ficará mais próxima ao eixo de y, quando maior o a não interceptará nenhum dos eixos. |
Crédito Parcial (CP) |
D2 |
A medida que o valor de a aumenta a reta vai ficando mais próxima do eixo y. |
Crédito Parcial (CP) |
D3 |
A reta passa pelo ponto origem, devido ao coeficiente angular ser positivo, a reta é crescente. |
Crédito Parcial (CP) |
D4 |
Quanto maior o parâmetro de a mais próximo ao eixo de y fica a reta, sendo crescente. |
Crédito Parcial (CP) |
D1: esta dupla faz o registro correto da situação até determinado momento, mas comete um erro na complementação da resposta. |
||
Quadro 2 – Análise da quarta categoria: O valor do parâmetro a ser positivo e o parâmetro b igual a zero
Fonte: os autores (2013)
A interpretação dos dados referente à categoria “O valor do parâmetro a ser positivo e o parâmetro b igual a zero” permite supor que há falta de entendimento do comportamento da função em relação ao coeficiente angular e o coeficiente linear. No que diz respeito ao coeficiente angular, a maioria afirma que a reta é crescente em função deste ser positivo e afirma que quanto maior for seu valor, mais próxima do eixo Oy a reta estará. No entanto, esta mesma maioria deixa de registrar que a reta passa pela origem do plano cartesiano e que este fato ocorre em função do valor atribuído ao parâmetro b (coeficiente linear). Dessa forma, pode-se afirmar que o fato do coeficiente linear ser nulo, levou os alunos a desconsiderarem as alterações ocorridas no comportamento gráfico da função e que possivelmente a visualização gráfica não se mostrou suficiente para que os alunos realizassem o registro corretamente.
Em seguida analisou-se os registros efetuados pelas duplas em relação a segunda categoria conforme descrito no Quadro 3.
Categoria: O valor do parâmetro a ser negativo e o parâmetro b igual a zero. |
||
Dupla |
Registro da dupla |
Avaliação |
D1 |
Reta decrescente, ela ficará mais próxima do eixo y, a reta também passa pelo ponto de origem. Ela não interceptará nenhum dos eixos. |
Crédito Parcial (CP) |
D2 |
Quanto maior o número negativo de “a”, a reta vai ficando próxima ao eixo, a diferença é que torna-se uma função decrescente neste caso. |
Crédito Parcial (CP) |
D3 |
A reta passa pelo ponto de origem, assim como no primeiro caso, o que difere as duas é o coeficiente angular, que neste caso é negativo. Sendo assim a reta será decrescente. |
Crédito Parcial (CP) |
D4 |
Quando os valores de a são negativos a reta é decrescente e quanto menor os parâmetros de a mais próximo do eixo de y fica a reta. |
Crédito Parcial (CP) |
D1: a dupla registra adequadamente que a reta é decrescente e que passará pela origem do plano cartesiano, porém faz afirmação indevida quando relata que a reta ficará mais próxima do eixo Oy e que não interceptará nenhum dos eixos. |
||
Quadro 3 – Análise da segunda categoria: O valor do parâmetro a ser negativo e o parâmetro b igual a zero
Fonte: os autores (2013)
A análise desta categoria possibilitou verificar novamente que os alunos não fizeram a relação do parâmetro b em relação a função interceptar a origem do plano cartesiano. Também é possível afirmar que há alunos que se confundem ao registrar por meio da escrita a quantificação em relação a números negativos e por este motivo fazem a afirmação de que quanto maior o parâmetro a mais próximo do eixo Oy a função estará. Acredita-se que o erro de registro em relação aos valores negativos do coeficiente angular seja um problema de registro, pois o software apresentou o comportamento gráfico da função na medida em que o valor do parâmetro era alterado.
No Quadro 4 apresenta-se a análise da terceira categoria que propõe a interpretação do comportamento da função quando da alteração do coeficiente angular e linear. Esta categoria, uma vez que a análise do coeficiente angular já foi realizada nas categorias anteriores, tem como objetivo demonstrar, especificamente, o comportamento da função ao se alterar o coeficiente linear.
Categoria: O valor do parâmetro a ser positivo ou negativo e o parâmetro b diferente de zero. Registro correto: Se a for positivo a reta será crescente, sendo que quanto maior o valor de a mais próximo do eixo Oy a reta estará e se o valor de a for menor, mais próximo do eixo Ox a reta ficará. Se a for negativo a resta será decrescente, sendo que quanto maior o valor de a mais próximo do eixo Oy a reta estará e se o valor de a for menor, mais próximo do eixo Ox a reta estará. Em relação ao parâmetro b, quando este é positivo ou negativo, a função intercepta o eixo Oy exatamente no valor determinado para ele. |
||
Dupla |
Registro da dupla |
Avaliação |
D1 |
A reta sempre interceptará o eixo de y no ponto a e se deslocará pelo eixo de x conforme o ponto b, sua classificação em crescente ou decrescente será determinada pelo a, positivo ou negativo, se b>0, ela se deslocará nos valores positivos em eixo y e nos valores negativos no eixo de x. Se b<0, ela se deslocará nos valores negativos do eixo y e positivos no eixo de x (se a>0). A reta não passará pelo ponto de origem do gráfico pois b≠0. Se b>0, a reta interceptará valores positivos tanto no eixo y como no eixo de x. Se b<0, a reta interceptará valores negativos tanto no eixo de y quanto no eixo de x (se a<0). |
Crédito Parcial (CP) |
D2 |
Quando o valor de a for positivo e b também positivo a reta assume valores positivos em y e negativos em x. Se a for negativo e b positivo os valores de x e y serão positivos. Se a for negativo e b negativo os valores de x serão positivos e os de y serão negativos. |
Nenhum Crédito (NC) |
D3 |
Neste caso, o coeficiente angular com valores positivos ou negativos, interceptará na condição da reta ser crescente ou decrescente. Alterando o coeficiente linear, ele desloca-se no eixo de y (valores + = para cima; valores neg (-): para baixo). |
Crédito Parcial (CP) |
D4 |
A reta de b se desloca no eixo de x para valores positivos a esquerda e valores negativos se deslocam para a direita. |
Crédito Parcial (CP) |
D1: a dupla faz o registro correto do comportamento gráfico da função em relação a alteração dos parâmetros, porém coloca informações adicionais que dificultam o entendimento daquilo que querem relatar e também cometem erro ao identificar qual o eixo do plano cartesiano a função irá interceptar. |
||
Quadro 4 – Análise da terceira categoria: O valor do parâmetro a ser positivo ou negativo e o parâmetro b diferente de zero
Fonte: os autores (2013)
Percebe-se que a visualização gráfica da função permite aos alunos identificarem o comportamento da função em relação aos parâmetros, porém em alguns casos é possível identificar que algumas duplas não conseguem fazer as relações corretas entre os coeficientes e o gráfico da função. Nesse sentido, pode-se dizer que ao investigar esta categoria os alunos comentem erros pelo fato de não se atentarem para situação como um todo.
No Quadro 5 tem-se a análise da última categoria que propõe a interpretação o comportamento da função quando não há inclinação da reta. Esta categoria, que analisa o coeficiente linear da função, objetiva demonstrar a função constante que é determinada pelo parâmetro b.
Categoria: O valor do parâmetro a ser igual a zero e o parâmetro b diferente de zero. |
||
Dupla |
Registro da dupla |
Avaliação |
D1 |
A reta sempre será paralela ao eixo de x, ela se deslocará no eixo de y conforme o ponto b. Se b>0, ela cortará o eixo de y em valores positivos. Se b<0, ela cortará o eixo de y em valores negativos. |
Crédito Parcial (CP) |
D2 |
Quando a for zero, o b≠0 a reta é constante. |
Crédito Parcial (CP) |
D3 |
Será uma reta constante, onde a mesma chegará o mais próximo do eixo de (x), porém sem intercepta-lo, neste caso. |
Crédito Parcial (CP) |
D4 |
Quando a for igual a 0 a reta só se desloca no eixo de y paralela a x com valores de b (+) se desloca para cima e valores de b negativos desloca para baixo. |
Crédito Parcial (CP) |
D1: Esta dupla faz o registro parcialmente correto, pois relata que a reta será paralela ao eixo Ox de acordo com o valor do parâmetro b, porém não registra que esta reta constante intercepta o eixo Oy exatamente no valor do parâmetro b. |
||
Quadro 5 – Análise da quarta categoria: O valor do parâmetro a ser igual a zero e o parâmetro b diferente de zero
Fonte: os autores (2013)
Nesta categoria é possível identificar, pelo registro efetuado pelos alunos, que eles entendem que a função na forma incompleta f(x)=b trata-se de uma função constante, ou ainda, uma reta paralela ao eixo Ox, porém não registram que o ponto de interseção entre a reta constante e o eixo Oy é exatamente no valor do parâmetro b.
Diante das análises realizadas, referente ao comportamento da função afim com base nos registros das quatro duplas, apresenta-se um metatexto sobre os registros realizados pelas duplas durante a atividade na intenção de apresentar quais as interpretações realizadas em função destes registros.
6. O metatexto
Aqui se relata a interpretação dos registros efetuados por cada dupla na tentativa verificar a aprendizagem do conceito de função afim por meio da utilização do software Geogebra, tendo em vista que estes alunos já tiveram contato com tal conceito.
A dupla D1 apresenta na atividade um bom aproveitamento do conceito de função afim, fazem os registros de acordo com o que visualizam no software, porém sempre na tentativa de complementar, ou ainda, melhorar a sua resposta, comentem erros nas informações adicionais. Acredita-se, tendo em vista a interpretação que a dupla realizou da atividade, que o erro na complementação da questão foi causado por uma desatenção no momento de registrar o nome dos eixos e até mesmo do ponto de interseção da reta e do eixo coordenado.
Já para a segunda dupla percebe-se que as informações apresentadas quanto ao conceito são parcialmente corretas por não descreverem as características da função de acordo com a situação analisada. Percebe-se que estes alunos não fizeram uma análise mais geral da situação estudada e em alguns momentos não perceberam os detalhes da função em relação a alteração dos parâmetros. Pode-se dizer esta dupla tem noção do conceito de função afim, porém não conseguiram entender quais as alterações causadas no comportamento gráfico da função quando da alteração dos seus parâmetros.
A penúltima dupla, assim como a anterior, apresenta registros parcialmente corretos, pois mostra em alguns momentos não ter conhecimento do conceito de função afim, mas em determinados momentos erram as informações. Tais erros podem ter sido cometidos por falta de atenção ou por desconhecimento de algumas particularidades da função afim e seus parâmetros. A dupla chega a relatar que o fato da função interceptar os eixos coordenados na origem do plano cartesiano ocorre por esta ter o coeficiente angular positivo, o que se pode dizer que é uma falta de domínio do conteúdo.
Da análise da última dupla pode-se dizer que fazem poucas observações a respeito do comportamento da função afim, não fazem menção quanto a classificação desta em relação ao coeficiente angular e nem quanto ao ponto de onde a reta intercepta o eixo Oy, apesar de comentar do comportamento da função constante em relação ao coeficiente linear. A dupla ainda comete um erro ao relatar o comportamento da função em relação ao coeficiente angular quanto este é negativo. Porém, o erro não é causado por desconhecerem o conceito de função afim, mas sim por não se atentarem a condição dos números negativos ao dizer qual número é maior que o outro.
Em resumo, apresenta-se abaixo, conforme Quadro 6, a avaliação realizada com base (categorias e unidades) nos registros feitos pelas duplas. Apenas uma das duplas não responde um dos momentos em relação ao comportamento da função afim, o que impossibilita afirmar que eles desconhecessem o conceito para que o registro correto fosse apresentado. No entanto, nenhum registro pôde ser considerado com crédito completo (CC), pois apresentavam informações incompletas.
|
Momento 1 |
Momento 2 |
Momento 3 |
Momento 4 |
||||||||
Duplas |
CC |
CP |
NC |
CC |
CP |
NC |
CC |
CP |
NC |
CC |
CP |
NC |
D1 |
- |
x |
- |
- |
x |
- |
- |
x |
- |
- |
x |
- |
D2 |
- |
x |
- |
- |
x |
- |
- |
- |
x |
- |
x |
- |
D3 |
- |
x |
- |
- |
x |
- |
- |
x |
- |
- |
x |
- |
D4 |
- |
x |
- |
- |
x |
- |
- |
x |
- |
- |
x |
- |
Total |
0% |
100% |
0% |
0% |
100% |
0% |
0% |
75% |
25% |
0% |
100% |
0% |
Quadro 6 – Análise quantitativa dos registros
Fonte: os autores (2013)
A análise dos registros da atividade permitiu compreender qual o conhecimento dos alunos em relação ao conceito de função afim além de indicar que possíveis erros são causados por desatenção dos alunos ou ainda por errarem conceitos matemáticos básicos que são considerados pré-requisitos. Tudo isso só foi permitido pela visualização dos gráficos criados no software Geogebra e pela possibilidade de simular graficamente, de modo dinâmico, as alterações em relação aos parâmetros da função afim. Além disso, assim como Borba e Villarreal (2005), acredita-se que
o conhecimento é produzido junto com uma dada mídia ou tecnologia da inteligência. Por esta razão, adotamos a perspectiva teórica que sustenta a noção que conhecimento é produzido por um coletivo composto de seres-humanos-com-mídias, ou seres-humanos-com-tecnologias, e não, como outras teorias sugerem, por apenas um ser humano individual, ou coletivo composto apenas de humanos (p. 23).
Assim, corrobora-se com Borba e Villarreal (2005) que o uso das tecnologias de informação e comunicação (TIC) contribui para a construção do conhecimento deixando de lado a noção ingênua de que estas são apenas auxiliares pedagógicos no processo de ensino e de aprendizagem.
7. Considerações finais
O objetivo deste estudo é verificar a aprendizagem do conceito de função afim pelos alunos por meio da utilização do software de geometria dinâmica Geogebra. Nesse sentido, a criação de um contexto, a atividade mediada pelo uso da TIC, permitiu identificar falhas no processo de ensino e aprendizagem de Matemática, falta de atenção dos alunos na interpretação da visualização gráfica dentre outros. Porém, evidenciou-se que o uso desse instrumento tecnológico contribui para construção do conhecimento pelos alunos, pois estes podem adquirir conceito, modifica-lo, e ainda, aprimorar aquele previamente aprendido.
Toda essa constatação da aprendizagem só foi possível mediante a análise dos registros criados pelos alunos durante a realização da atividade. Apesar de os registros escritos permitirem algumas interpretações sobre os aspectos da função afim, baseados na análise de conteúdo, percebeu-se que o confronto de uma gravação dos diálogos dos alunos no desenvolvimento da atividade poderia contribuir para compreender alguns erros. No entanto, como não se efetuou a gravação, pode-se dizer que o registro escrito revelou certa falta de domínio do conceito de função afim e que as duplas cometeram equívocos na interpretação da visualização do gráfico gerado pelo software.
A atividade propiciou verificar o entendimento dos alunos sobre o conteúdo abordado na atividade bem como a percepção da necessidade de retomada do conceito de função afim com o auxílio do software Geogebra para que os alunos consigam interpretar a visualização gráfica proporcionada por esta TIC e assim modifiquem os conhecimentos anteriormente assimilados.
Todo esse processo possibilitou perceber uma falha no processo de ensino e de aprendizagem que mostrou a necessidade de retomar o conceito de função afim e de rever a prática docente de modo a pensar em diferentes formas de ensino de conceitos. Também se verificou que a aplicação de uma atividade na qual os alunos tem a possibilidade de manipular a TIC e registrar o que ele visualiza, fazendo conexões com conceitos prévios, permite a construção de conhecimentos além de permitir que estes tenham contato com outra forma de ensina e aprender. Este tipo de atividade poderá ser utilizado por estes acadêmicos no momento de ensinar a Matemática para seus alunos, já que se trata de um curso de licenciatura e entende-se como necessário o uso das TIC em sala de aula de modo a favorecer a construção do conhecimento pelos alunos e chamar a atenção destes para a aula mesmo com toda a presença da pós-modernidade na escola.
Referências bibliográficas
Buriasco, R. L. C., Cyrino, M. C. C. T. y Soares, M. T. C. (2004). Um estudo sobre a construção de um manual para correção das provas com questões abertas de matemática – AVA2002. En: Anais do VIII Encontro Nacional de Educação Matemática, Educação Matemática: um compromisso social, Recife:SBEM.
Bogdan, R. y Biklen, S. (1994). Investigações qualitativas em educação: uma introdução à teoria e aos métodos. Porto: Ed. Porto.
Bardin, L. (2009). Análise de conteúdo. Lisboa: Edições 70.
Borba, M. C. y Villareal, M. E. (2005). Humans-with-media and the reorganization of mathematical thinking: information and communication technologies, modeling,experimentation and visualization. New York: Springer.
Momo, M. y Costa, M. V. (2010). Crianças escolares do século XXI: para se pensar uma infância pós-moderna. Cadernos de Pesquisa, v. 40, n. 141, p. 965-991. Recuperado el 15 de marzo de 2013, de http://www.scielo.br/pdf/cp/v40n141/v40n141a15.pdf.
Moraes, R. (1999). Análise de conteúdo. Revista Educação. Porto Alegre, n.37, ano XXII, p.7-31. Recuperado el 18 mayo de 2013, de http://cliente.argo.com.br/~mgos/analise_de_conteudo_moraes.html.
Steinbring, H. (2005). The construction of new mathematical knowledge in classroom interaction: an epistemological perspective. Dordrecht: Springer.
Valente, J. A. (1999). O computador na sociedade do conhecimento. En: Valente, J. A. (Org.) O computador na sociedade do conhecimento. Campinas: UNICAMP/NIED.