1. Introdução
Tradicionalmente um dos problemas da organização da produção está em como utilizar o conhecimento do operador na melhoria e organização do processo e das operações (Liker, 2004). Estudos como os de Karim e Zaman (2013), Plebani (2009), Saurin et al (2008) e Xiaobo e Ohno (2000) ilustram a dificuldade em transferir para os operadores a responsabilidade em gerir e controlar os seus processos e operações. Por meio destes estudos é possível observar que independentemente do contexto (manufatura de componentes, construção civil, linhas de montagem, operações em laboratórios) a busca pela implementação da autonomação gera dificuldades e insegurança sobre os operadores e os implementadores.
Essas dificuldades e inseguranças despontam do conceito de autonomação, originalmente evocado por Ohno (1997), que entende que a máquina é dotada de inteligência humana e, portanto, é facultado ao operador ou à máquina a autonomia de parar o processamento sempre que for detectada qualquer anormalidade. Olhando isto sob a perspectiva empresarial a interrupção do processo é contraditória as metas de manufatura de uma organização (Klippel, 2007). Dessa forma, parar o processo é uma medida reativa a perda, enquanto que medidas pró-ativas são mais indicadas para o controle de perdas (Saurin et al, 2012).
Este panorama sugere que métodos de controle onde a autonomia dos operadores seja valorizada e acompanhada de ferramentas de controle, merece análise. Alternativamente, este estudo abordará a questão da autonomação combinada a experimentos fatoriais. Os experimentos fatoriais são aqueles que duas ou mais séries de tratamentos (fatores) são aplicadas simultaneamente no mesmo experimento. Os níveis dos fatores são combinados entre si para formar uma relação de tratamentos a serem avaliados num mesmo experimento, conduzido de acordo com um delineamento experimental adequado às condições de uniformidade das unidades experimentais. A interação entre os fatores é a mais importante situação a ser verificada, e sendo essa significativa o desdobramento dos fatores torna-se necessário. Entretanto, assim como no caso uni-variado quantitativo, no caso bi-variado com duas variáveis quantitativas utiliza-se análise de regressão múltipla para obter-se a estimativa do ponto de máxima eficiência relativa.
Segundo Juran (1974), o objetivo geral na experimentação é identificar quais as variáveis são mais importantes para um determinado processo. Sendo as variáveis mais importantes conhecidas, a questão é entender como essas variáveis interferem no processo. Caso elas sejam quantitativas, Juran (1974) indica que a resposta será dada através da investigação de superfície de resposta, que aplica a técnica de Análise de Superfície de Resposta (ASR). De acordo com Montgomery (2004) o objetivo da ASR é otimizar a resposta associada aos fatores do experimento. Além disso, essas alterações podem ser efetuadas na linha produtiva, visto que no chão de fábrica podem-se buscar pequenas e planejadas alterações nas condições de operação (Juran, 1974). O conjunto de procedimentos adotados para gerar essas modificações no chão de fábrica é denominado Operação Evolucionária (EVOP) e consiste na simplificação da ASR.
Sob este contexto o objetivo deste estudo é aplicar EVOP em um conjunto de dados de um estudo sobre a carbonatação do concreto com sílica ativa na construção civil, e verificar como ferramentas de ASR podem auxiliar no processo de implementação da autonomação em ambientes de transformação física de materiais.
2. Fundamentação teórica
Superfície de resposta, segundo Montgomery (2001, 2004) é uma coleção de técnicas matemáticas e estatísticas que são usadas para modelar e analisar problemas em que a resposta de interesse é influenciada por vários fatores quantitativos e cujo objetivo é otimizar a resposta. Assim, supondo que uma dada experimentação é conduzida com dois fatores (x1 e x2) e uma variável de resposta (y) é observada, tem-se que:
![]()
onde: ε representa o ruído ou resíduo observado na resposta y. Se for definido que a resposta esperada é ![]() , então a superfície representada por
, então a superfície representada por
![]()
é denominada superfície de resposta.
Usualmente a superfície de resposta é representada através de gráficos 3-D, onde ![]() é plotado contra os níveis x1 e x2. A representação através de curvas de nível também é muito usual.
é plotado contra os níveis x1 e x2. A representação através de curvas de nível também é muito usual.
Na maior parte dos problemas, segundo Montgomery (2001), a relação entre os fatores e a resposta não é conhecido e, então, uma aproximação razoável da função que relaciona y e o conjunto de variáveis independentes deve ser obtida. Assim, uma função de ordem mais baixa deve ser modelada (uma função linear das variáveis independentes) e esta é representada por
![]()
sendo: ![]() os coeficientes do modelo de regressão e k é o número de variáveis independentes no modelo.
os coeficientes do modelo de regressão e k é o número de variáveis independentes no modelo.
A partir de uma aproximação razoável, em que os níveis das variáveis independentes encontram-se próximos do ponto de ótimo, uma modelagem de maior ordem deve ser efetuada, principalmente se pode ser observada uma curvatura na superfície. Assim, um modelo de segunda ordem deve ser ajustado e este modelo é representado por
![]()
e segundo Montgomery (2001) praticamente todos os problemas podem ser resolvidos pelos modelos de primeira e segunda ordem apresentados nas equações 3 e 4.
É importante ressaltar que este é um procedimento sequencial. Assim, a cada resultado obtido com o ajuste de um modelo, as variáveis independentes devem ser ajustadas em seus níveis a fim de que o sistema caminhe na direção do ponto de resposta ótima (ponto de máxima eficiência relativa). Assim, um novo experimento fatorial deve ser efetuado com os níveis dos fatores atualizados a fim de apurar, a cada nova etapa, a resposta.
Quanto ao planejamento do experimento, o mais comum é a utilização de delineamentos do tipo 2k, adicionado de 1 a 3 repetições no ponto central para estimativa do erro experimental (Montgomery, 2001; Juran, 1974). Um dos projetos de experimentos mais comuns é o delineamento composto central estrela, apresentado na Tabela 1 e Figura 1.
Tabela 1 - Delineamento composto central estrela com 3 repetições no ponto central
Repetições |
x1 |
x2 |
1 |
-1,000 |
-1,000 |
2 |
-1,000 |
1,000 |
3 |
1,000 |
-1,000 |
4 |
1,000 |
1,000 |
5 |
1,414 |
0,000 |
6 |
-1,414 |
0,000 |
7 |
0,000 |
1,414 |
8 |
0,000 |
-1,414 |
9 |
0,000 |
0,000 |
10 |
0,000 |
0,000 |
11 |
0,000 |
0,000 |
A Tabela 1 apresenta as variáveis codificadas cujos valores são obtidos através dos valores mínimos e máximos das variáveis observadas. Note que as repetições 5, 6, 7 e 8 exigem a execução de unidades amostrais além dos limites usuais de operação do sistema. Estas unidades amostrais são obtidas, no projeto, pela rotação do quadrado formado pelas observações 1, 2, 3 e 4 em 45 graus, conforme pode ser visualizado na Figura 1.
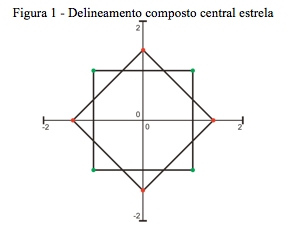
A análise deste tipo de projeto experimental leva em consideração a existência de fatores significativos tanto no modelo de primeira quanto no modelo de segunda ordem. De fato, uma vez que o modelo de segunda ordem tenha apresentado fatores significativos, a vizinhança do ponto ótimo foi encontrada e este já poderá ser identificado. Entretanto, uma vez que o modelo de segunda ordem não foi significativo, deslocamentos no sentido da máxima inclinação do modelo de primeira ordem devem ser efetuados.
A identificação da direção, bem como a própria análise dos resultados envolvem alta complexidade matemática e estatística. Assim, em projetos que envolvam a otimização de processos, é comum a contratação de especialistas para utilização destas ferramentas, o que gera aumento nos custos da qualidade. Uma estratégia simples, e que pode ser implantada pela gerência, foi proposta por George Box, na década de 60. A operação evolucionária, do inglês evolutionary operation (EVOP) é um método de monitoramento dos parâmetros variáveis de um processo que não necessita da parada da produção para ser realizado, que tem o mínimo envolvimento da engenharia, podendo ser conduzido inclusive pela equipe operacional.
Frequentemente o EVOP é utilizado em operações de processos de larga escala permitindo assim que informações sobre os parâmetros monitorados auxiliem na melhoria do processo, resultando desta forma em melhoria contínua do produto.
EVOP é um método de monitoramento e melhoria contínua de processos cujo objetivo é mover as condições operacionais na direção do ótimo. Para sua elaboração alguns quesitos básicos de delineamento de experimentos são utilizados. Juran (1974) e Montgomery (2004) apresentam o método EVOP construído a partir do delineamento composto central quadrado utilizado em ASR e apresentado na Figura 2.
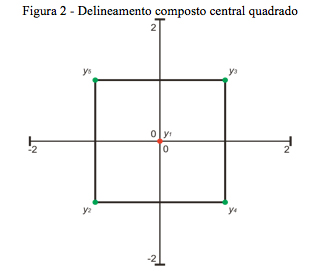
Como o EVOP é uma simplificação do ASR, o objetivo é a construção de uma superfície simplificada (possível de ser compreendida no chão de fábrica) onde se busca a otimização da função apresentada na equação (1). Portanto, é importante ressaltar que apenas pequenas alterações nos níveis dos parâmetros podem ser introduzidas. Pequenas para que não ocorram perturbações sérias na qualidade do produto, mas grandes o suficiente para que eventualmente se descubram melhorias potenciais no desempenho do processo.
As respostas observadas (yi) na Figura 2 são obtidas e os efeitos principais podem ser calculados através das expressões (5) e (6). O efeito da interação pode ser obtido através da expressão (7).
Dessa maneira calculam-se os efeitos de x1, x2 e sua interação, substituindo as observações individuais yi nas equações (5), (6) e (7) pelas médias ![]() das n observações em cada ponto.
das n observações em cada ponto.
![]()
![]()
![]()
Pode-se observar um efeito significante das variáveis ou de sua interação sobre a variável resposta y. Quando isso ocorre, deve-se tomar a decisão de mudar as condições básicas de operação a fim de melhorar o resultado do processo. Em geral, utiliza-se o ponto central como estimativa do erro experimental, visando testar a significância dos efeitos através de um teste F, como o da análise de variância. Tendo as condições detectadas e melhoradas, conclui-se uma fase e inicia-se uma nova fase através de um novo ciclo.
EVOP pode também ser utilizado para o monitoramento do processo devido a flutuações que possam ocorrer em torno do ótimo previamente identificado em uma ASR. A vantagem deste método é que seus resultados, de qualquer modo, convergem com menor precisão para os resultados obtidos na ASR, porém com maior simplicidade.
Segundo Juran (1974), sendo conservador, a evolução deve ser contínua, mantendo na fase seguinte, pontos já utilizados na fase anterior. A figura 3 apresenta alguns exemplos de movimentação da fase antiga para a nova fase sob este aspecto. A figura 3(a) apresenta um movimento de troca de fase, tendendo a uma melhor resposta, para um maior uso ou quantidade da variável independente B e um menor uso ou quantidade da variável independente A, no entanto utilizando os valores de ponto central (1) e superior esquerdo (5) da fase antiga.
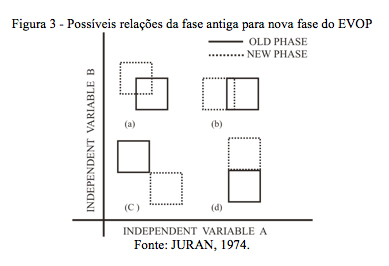
3. Metodologia
Este trabalho utilizou o projeto de experimentos utilizado por Possan et al., 2006 que avaliou as variáveis de resposta de carbonatação e resistência à compressão axial do concreto com limites máximos e mínimos no experimento. No estudo em questão foi utilizado a ASR sobre dados oriundos dos experimentos de Kulakowski (2002). Dessa forma, aplicar-se-á nos resultados obtidos na primeira etapa da ASR o método EVOP, e assim sucessivamente até que se encontrem ou não discrepâncias entre os resultados da ASR e os do EVOP.
No estudo em questão foram adotados 5 níveis para as variáveis: relação água/aglomerante e teor de adição de sílica ativa. Na aplicação do EVOP utilizou-se, inicialmente, apenas os níveis intermediários de cada variável mais o ponto central, construindo assim um delineamento composto central quadrado (2²) ao invés do delineamento 25 utilizado no estudo original de Possan et al., 2006. Esta aplicação limitou-se em avaliar as respostas somente da profundidade de carbonatação, pois não é foco desse trabalho à avaliação da relação entre carbonatação e resistência à compressão do concreto, mas sim a validade do método estatístico.
Os níveis das variáveis podem ser visualizados junto com os resultados na Tabela 2. Além disso, os resultados foram avaliados em diferentes períodos de tempo (idade do concreto), sendo eles 7, 28, 63 e 98 dias. Efetuou-se a avaliação a partir dos dados de 98 dias de resposta de carbonatação, pois esta foi uma das idades do concreto analisadas com a ASR por Possan et al. (2006).
Tabela 2 - Profundidade de carbonatação observada (mm) em 98 dias
Sílica Ativa (%) |
Relação Água/Aglomerante |
||||
0,30 |
0,35 |
0,45 |
0,60 |
0,80 |
|
0 |
0,06-0,00 |
|
0,58-0,00 |
|
16,50-16,30 |
5 |
|
0,14-0,00 |
|
3,29-3,85 |
|
10 |
0,07-0,00 |
|
0,68-0,00 |
|
19,30-18,40 |
15 |
|
0,18-0,00 |
|
4,13-5,17 |
|
20 |
0,09-0,00 |
|
0,90-0,00 |
|
25,40-27,00 |
Resultados do primeiro e segundo corpo de prova respectivamente
Fonte: Possan et al., 2006.
Neste estudo, foram moldados dois corpos de prova de cada betonada os quais foram utilizados como ciclos dentro de uma mesma fase do EVOP. Quanto à mudança de fase, utilizaram-se os mesmos dados a fim de identificar o caminho percorrido pelo EVOP e por fim, comparar com a superfície de resposta obtida por Possan et al. (2006).
Note que um ciclo não é suficiente para detectar mudanças no processo e se não são identificados efeitos significativos entre 5 a 8 ciclos, isto é um forte indício de que estes efeitos não estão presentes na faixa investigada do processo. Isto quer dizer que o processo pode já estar no ponto ótimo destes fatores.
A aplicação do método EVOP foi efetuada com auxílio de planilhas eletrônicas do Microsoft® Office Excel e as mesmas podem ser solicitadas aos autores.
4. Resultados
A Tabela 2 apresentou os resultados obtidos nas duas betonadas do estudo efetuado por Possan et al. (2006) que serão utilizados nesta simulação. Foram então utilizados os resultados obtidos no primeiro corpo de prova como sendo o observado no primeiro ciclo do EVOP e os resultados do segundo corpo de prova como os observados no segundo ciclo. Para efeito de análise, considerou-se a relação água/aglomerante como fator 1 e sílica ativa (%) como fator 2.
Para o primeiro ciclo da fase 1, foram considerados os níveis de fatores conforme a Tabela 3, cujas respostas observadas yi constam na Tabela 2 (primeiro corpo de prova).
Tabela 3. Níveis dos fatores para fase 1 do EVOP
Respostas |
Relação Água/Aglomerante |
Sílica Ativa |
y1=0,68 |
0,45 |
10 |
y2=0,18 |
0,35 |
15 |
y3=3,29 |
0,60 |
5 |
y4=4,13 |
0,60 |
15 |
y5=0,14 |
0,35 |
5 |
A Figura 4 apresenta os resultados do ciclo da fase 1 do EVOP simulado. Nesta etapa, são calculados somente os efeitos dos fatores, não sendo possível estimar a variabilidade entre ciclos, o que definirá a significância dos fatores e de sua interação.
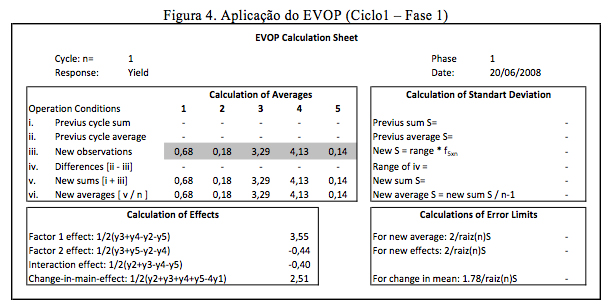
No ciclo 2, os resultados do segundo corpo de prova apresentados na Tabela 2 são lançados como “novas observações” na linha iii da Figura 5. Neste ciclo torna-se possível estimar a variabilidade entre as observações dos ciclos e calcular os limites de erro. No caso de algum efeito calculado através das equações (5) a (7) ser maior do que o erro estimado deve-se tomar a decisão de alterar as condições de produção. Pode-se observar na Figura 5 que o efeito 1 observado é significativo, pois seu resultado é maior do que os limites de erro calculados (4,03 > 0,73).
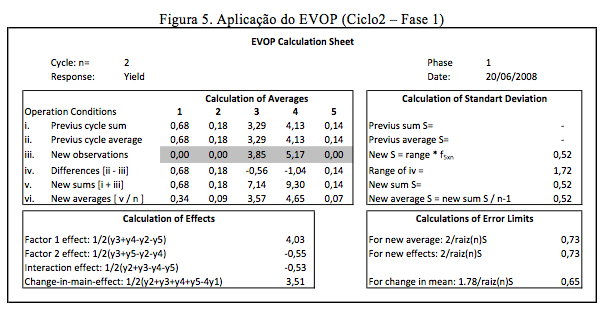
Ressalta-se que os efeitos do fator 2, assim como o efeito da interação, são números negativos e se, em módulo fossem maiores do que os limites do erro calculados, também configurariam a significância destes fatores. O fato de se ter fatores significativos implica que o processo não está operando em condições ótimas e deve ser alterado. Decide-se então pela alteração das condições de operação, concluindo-se a primeira fase e ingressando na segunda fase do EVOP.
Observa-se ainda na Figura 5 (Ciclo 2 – Fase 1) que a menor média entre os tratamentos (Linha vi. da figura) refere-se ao tratamento 5. No caso da profundidade de carbonatação, quanto menor for esta profundidade, melhor será a durabilidade do concreto. Deste modo, a direção de movimentação do EVOP deve seguir no sentido de abandonar o tratamento de maior média, deslocando-se, neste caso, diagonalmente para cima à esquerda sobre os valores da Tabela 2, como exibido na Figura 3(a).
Na segunda fase, o procedimento se repete, não sendo possível tomar decisões a partir primeiro ciclo. Pode-se dizer que o primeiro ciclo é apenas coleta de dados, pois análises são possíveis de ser efetuadas somente a partir do segundo ciclo de cada fase, quando se podem determinar estimativas de variabilidade. As Figuras 6 e 7 apresentam os ciclos 1 e 2 da fase 2 do EVOP a partir dos dados da Tabela 2, deslocando-se no sentido definido no ciclo 2 da fase 1.
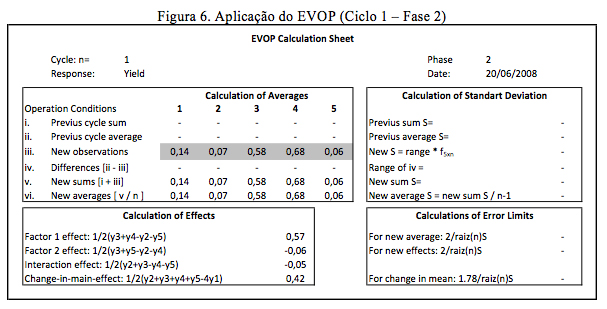
Observa-se no ciclo 2 da fase 2 que o efeito do fator 1 é novamente significativo, devido ao efeito calculado ser maior do que o limite do erro calculado (0,28 > 0,26). Logo, pode-se considerar o final desta fase e a direção da evolução deve ser efetuada considerando os menores valores médios dos tratamentos. Neste caso observa-se que a menor média refere-se novamente ao tratamento 5. Deste modo, a direção a ser seguida é similar a da fase anterior.

No estudo efetuado por Possan et al.(2006) os resultados observados na ASR são apresentados na Figura 8. Observa-se que para menores níveis de sílica ativa e menores valores de água/aglomerante a superfície de resposta tende a medida de zero milímetro de profundidade de carbonatação.
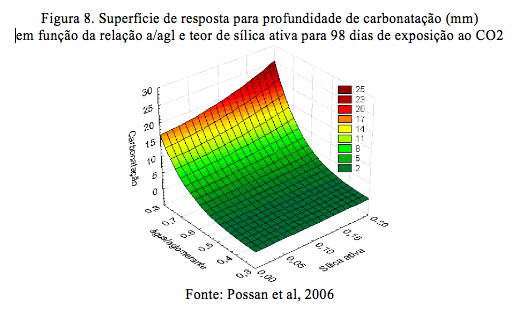
5. Considerações finais
A importância da utilização do EVOP está na busca contínua de melhorias, mesmo com o processo de produção em andamento. Sua simplicidade de utilização e a qualidade das informações obtidas com seu emprego são importantes, visto que permitem resultados similares aos da implantação de ASR, porém com custos significativamente menores.
Do mesmo modo que na ASR, o exemplo de aplicação do método EVOP mostrou que este é capaz de direcionar o aprimoramento do processo, através de resultados melhores na variável de resposta. Destaca-se que uma terceira fase não pode ser avaliada devido à falta de continuidade de observações do estudo original, que não atingiu o ponto ótimo. O último ciclo da fase 2, já indicava a necessidade de nova mudança de fase, apontando o mesmo sentido de evolução. No caso do exemplo, é preciso atentar que devem ser considerados os valores práticos mínimos dos fatores considerados. Um exemplo é a redução da relação de água e aglomerante, que possui uma limitação prática na mistura dos materiais.
Pode-se considerar que o método EVOP, apesar de possuir aplicação mais simplificada, apresentou sensibilidade suficiente com relação ao grau de detalhamento e precisão, complementado pela facilidade de uso necessária ao setor produtivo.
Quanto à questão da viabilização da autonomação com as técnicas de experimentos, verifica-se uma real aplicabilidade. As técnicas de experimentos atuam de forma preventiva, detectando o erro ou uma falha, como mostrado no caso anterior. Dessa forma, será garantindo que operador ou máquina interrompa o processo sob a justificativa de adequação ou melhoria, comprovada diretamente com dados do processo. Sob essa lógica, é possível assumir que aspectos culturais que imporiam a parada da operação ou do processo, passariam ao segundo plano.
Espera-se que novos estudos sejam realizados, a fim de justificar essa proposição inicial, permitindo dessa forma um desenvolvimento detalhado de como seria a readequação da autonomação em sistemas de produção que seguem o modelo Toyota de produção.
6. Referências
AZHARUL KARIM, A., ZAMAN, K. (2013) A methodology for effective implementation of lean strategies and its performance evaluation in manufacturing organizations. Business Process Management Journal, v.19, n.1, p.169-196.
JURAN, J. M. (1974) Quality control handbook. New York: McGraw-Hill Inc, 3 ed.
KLIPPEL, A. F. (2007) Implementação da gestão enxuta em empresas de mineração a partir de um modelo de gestão integrada: uma perspectiva de sinergia entre a engenharia de minas e a engenharia de produção. Tese de Doutorado. Universidade Federal do Rio Grande do Sul.
KULAKOWSKI, M. P. (2002) Contribuição ao estudo da carbonatação em concretos e argamassas compostos com adição de sílica ativa. 2002. (Tese em engenharia) – Curso de Pós Graduação em engenharia de Minas, Metalúrgica e de Materiais, Universidade Federal do Rio Grande do Sul. Porto Alegre.
LIKER, J. K. (2004) The Toyota Way. McGraw-Hill Education (India) Pvt Limited, p.97-163.
MONTGOMERY, D. C. (2001) Design and analysis of experiments. New York: John Wiley & Sons, Inc., 5 ed.
MONTGOMERY, D. C. (2004) Introdução ao Controle Estatístico da Qualidade. Rio de Janeiro: Livros Técnicos e Científicos Editora S.A., 4 ed.
OHNO, T. (1997) O Sistema Toyota da Produção: além da produção em larga escala. Porto Alegre: Bookman, p.63-87.
PLEBANI, M. (2009) Does POCT reduce the risk of error in laboratory testing? Clinica Chimica Acta, v.404, n.6, p.59-64.
POSSAN, E. et al. (2006) Emprego da metodologia de superfície de resposta no estudo da carbonatação do concreto com sílica ativa. CBC2006 Congresso Brasileiro do Concreto, anais. Rio de Janeiro-RJ.
SAURIN, T. A., FORMOSO, C. T., CAMBRAIA, F. B. (2008) An analysis of construction safety best practices from a cognitive systems engineering perspective. Safety Science, v.46, n.8, p.1169-1183.
SAURIN, T. A., RIBEIRO, J. L., VIDOR, G. (2012) A framework for assessing poka-yoke devices. Journal of Manufacturing Systems, v.31, n.3, p.358-366.
XIAOBOA, Z., OHNO, K. (2000) Properties of a sequencing problem for a mixed model assembly line with conveyor stoppages. European Journal of Operational Research, v.123, n.1, p.560-570.